邏輯回歸的參數調節
參數展示?
LogisticRegression(penalty='l2',dual=False,tol=1e4,C=1.0,fit_intercept=True,intercept_scaling=1,class_weight=None,random_state=None,solver='liblinear',max_iter=100,multi_class='ovr',verbose=0,warm_start=False, n_jobs=1)
在前面的學習中，我們參數使用的都是默認參數。所有在面對特殊問題的時候，準確率會高，召回率也不高。所以我們要對某些數據進行微調。?
正則化懲罰項
? ? ? ? 在我們處理數據的時候，有時候會出現各種各樣的數據，然后根據數據我們也有各種各樣的權重參數，例如下面有兩種權重參數
????????data:1,1,1,1
? ? ? ? w1：1，0，0，0
? ? ? ? w2：0.25，0.25，0.25，0.25
在兩組參數中，我們得到的最終結果都是一樣的，那我們知道，第一種肯定不行，過擬合了，不能運用所有數據，但是我們該如何讓機器也知道，什么樣的權重參數好，什么壞呢？
這里在均方差中引入了正則化懲罰項
????????????????????????
?正則化懲罰項?
λR(W)- λ: 正則化強度系數（超參數）也就是參數中的C
- R(W): 權重的懲罰函數，包含兩種形式：
- ?L1 正則化?:
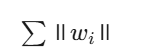
- 產生稀疏權重，自動特征選擇
- ?L2 正則化?:
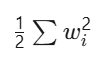
- ?為求導便利設計的系數（梯度計算時抵消平方項導數產生的2）
- 控制權重幅度，防止過擬合
- ?L1 正則化?:
?其實正則化最重要的功能也就是防止過擬合
交叉驗證
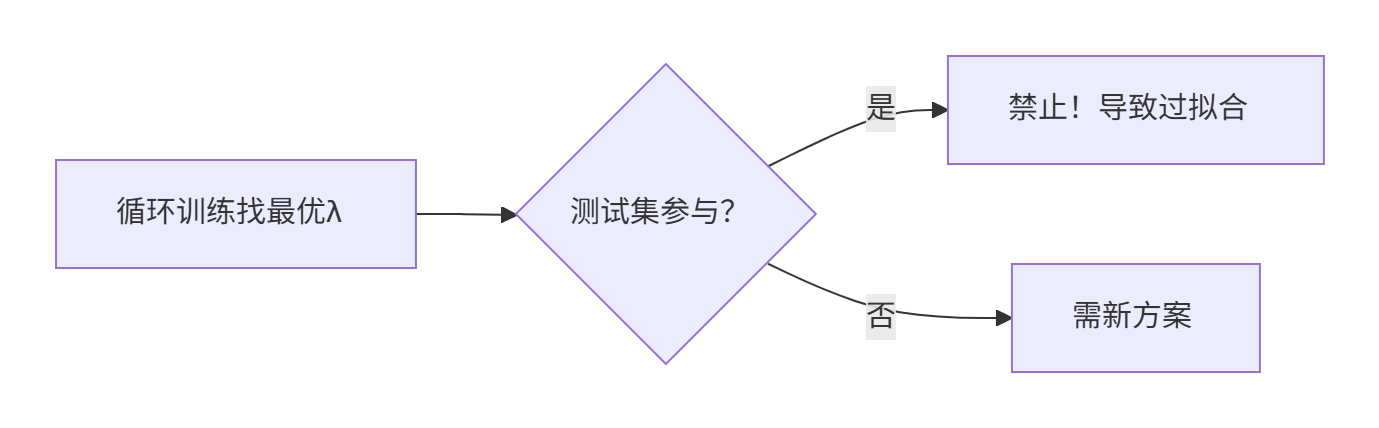
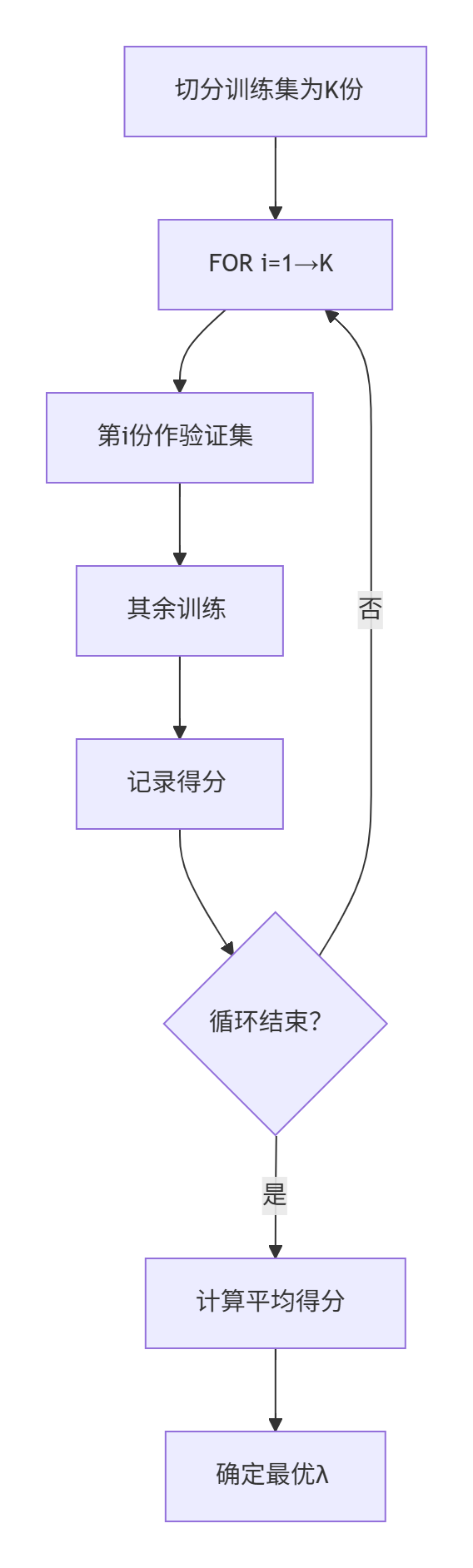
? ? ? ? 對于上面的正則化懲罰項系數，我們該怎么知道哪個闡述最好呢？我們會想到讓機器循環找到那個最好的參數。
????????于是我們想到循環訓練，讓測試集來測試，選擇出一個最好的參數，但是我們注意到，如果我們讓測試集參與到了訓練中，這樣結果會不會也會有過擬合的現象，所有我們無論如何也不能把測試集參與到訓練中。
下面我們又想到，可以把訓練集中劃出一部分來進行驗證，是不是也可以。但是我們又想著一直用這一個驗證集會不會也會過擬合。
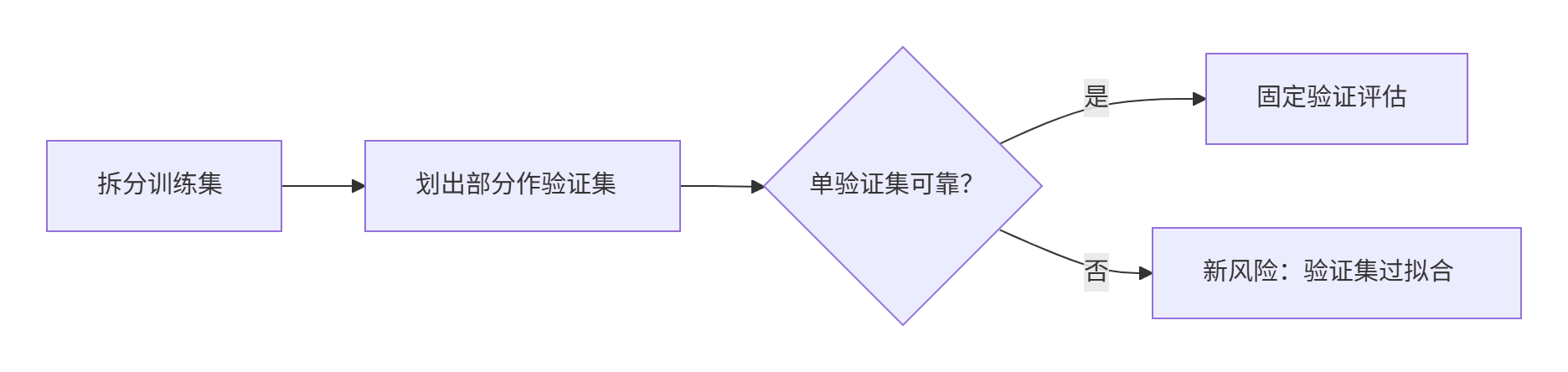接下來，我們想到，我們可以把訓練集切成幾份，循環到一個參數時，依次把幾份中的一個當作驗證集，其余訓練。然后去他們的平均值作為我們的最終結果。這樣就是我們的交叉驗證了！
代碼實例
import pandas as pd
from numpy.ma.core import count
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
data=pd.read_csv(r'D:\培訓\機器學習\邏輯回歸\銀行貸款\creditcard.csv')
print(len(data[data['Class'] == 1]))
mod=StandardScaler()
data["Amount"]=mod.fit_transform(data[['Amount']])
X=data.drop(["Time","Class"],axis=1)
y=data["Class"]
train_X,test_X,train_y,test_y=train_test_split(X,y,test_size=0.2,random_state=42)from sklearn.model_selection import cross_val_score
import numpy as np
scores=[]
pe=[0.01,0.1,1,10,100]
for p in pe:lr=LogisticRegression(C=p,penalty ='l2',random_state=42,max_iter=1000)score=cross_val_score(lr,train_X,train_y,cv=8,scoring='recall')scores_mean=sum(score)/len(score)scores.append(scores_mean)print(scores_mean)best_c=pe[np.argmax(scores)]
print('最優系數：',best_c)
model=LogisticRegression(C=best_c,penalty ='l2',random_state=42,max_iter=1000)
model.fit(train_X,train_y)
print(model.score(test_X,test_y))
from sklearn import metrics
print(metrics.classification_report(test_y,model.predict(test_X)))?上面我們取了[0.01,0.1,1,10,100]這幾個值來進行測試，然后找出最優的值。下面我們對代碼核心部分for循環中的部分進行解讀
先建立模型
?????lr=LogisticRegression(C=p,penalty ='l2',random_state=42,max_iter=1000)計算召回率的得分值
? score=cross_val_score(lr,train_X,train_y,cv=8,scoring='recall')求均值，并把值添加到列表中。
? scores_mean=sum(score)/len(score)scores.append(scores_mean)找出最大值
best_c=pe[np.argmax(scores)]根據最優參數進行訓練
model=LogisticRegression(C=best_c,penalty ='l2',random_state=42,max_iter=1000)
model.fit(train_X,train_y)
print(model.score(test_X,test_y))
from sklearn import metrics
print(metrics.classification_report(test_y,model.predict(test_X)))得出結果?
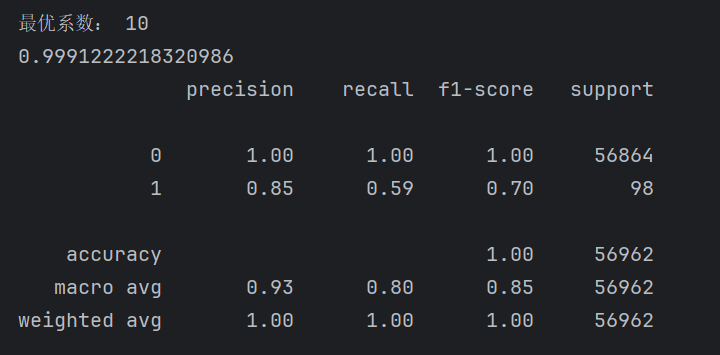
下面這個是沒有進行交叉驗證時候的結果
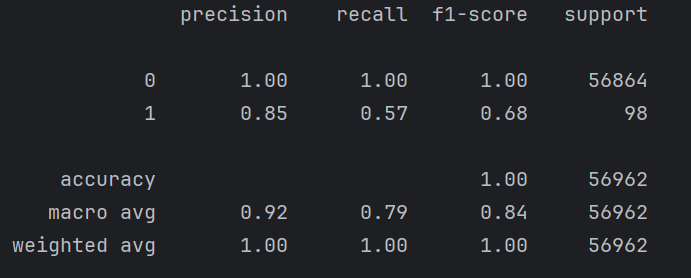
召回率僅僅增加了百分之二，但是如果對于后期增加百分之二也很重要，這里主要是數據類別的極度不均衡。下面我們對數據進行處理?
數據處理
????????我們數據中的，類別為1的和為0的數據差了幾千倍，并且我們比較關注為1的結果，所以我們要對數據進行處理，也就是兩條路，一個是增加1的數據量，或者減少0的數據量。
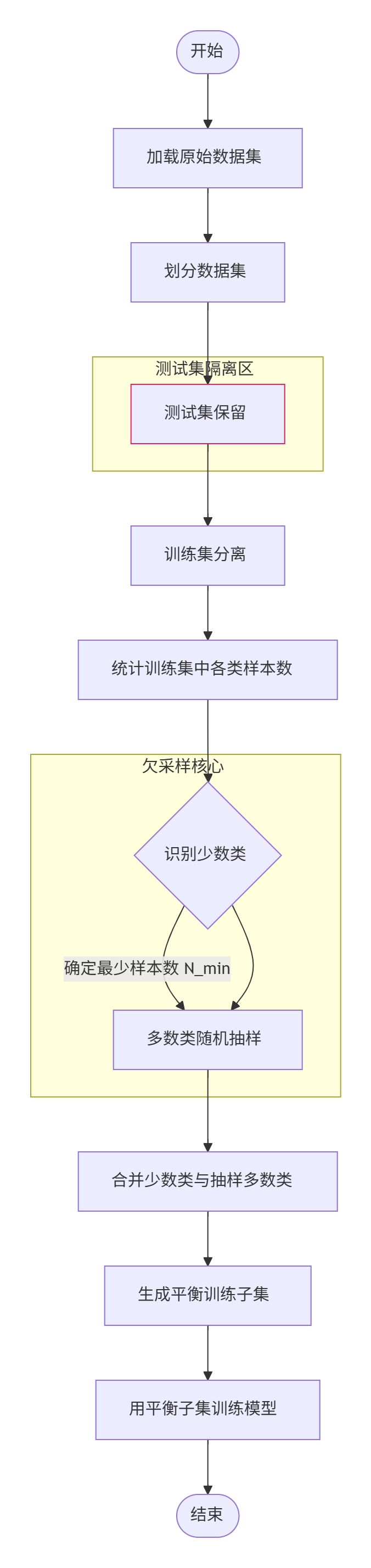
下采樣
這個是訓練集中0的數據量。我們想先對數據集進行劃分，測試集不處理，訓練集進行處理，先找出少的那一類的數據條數，然后對數據多的那一類進行抽樣，抽出相同數量的數據，然后針對這些進行訓練。
代碼部分
train_data,test_data=train_test_split(data,test_size=0.2,random_state=42)pe=train_data[train_data['Class'] == 1]
ne=train_data[train_data['Class'] == 0]d1 = ne.sample(len(pe))train_data = pd.concat([d1,pe])train_X=train_data.drop(["Time","Class"],axis=1)
train_y=train_data["Class"]
test_X=test_data.drop(["Time","Class"],axis=1)
test_y=test_data["Class"]其余沒修改，就這一部分修改了?
上面代碼中，我們先對訓練集和測試集進行分開，然后對訓練集中標簽為0的標簽中取樣出標簽0數量的數據，然后進行連接，下面就正常訓練了，不夠這樣可能會讓數據量減少許多
過采樣
這個是讓數據量少的那一類增加，不夠也不是隨便增加，其中采用了SMOTE算法，如下：
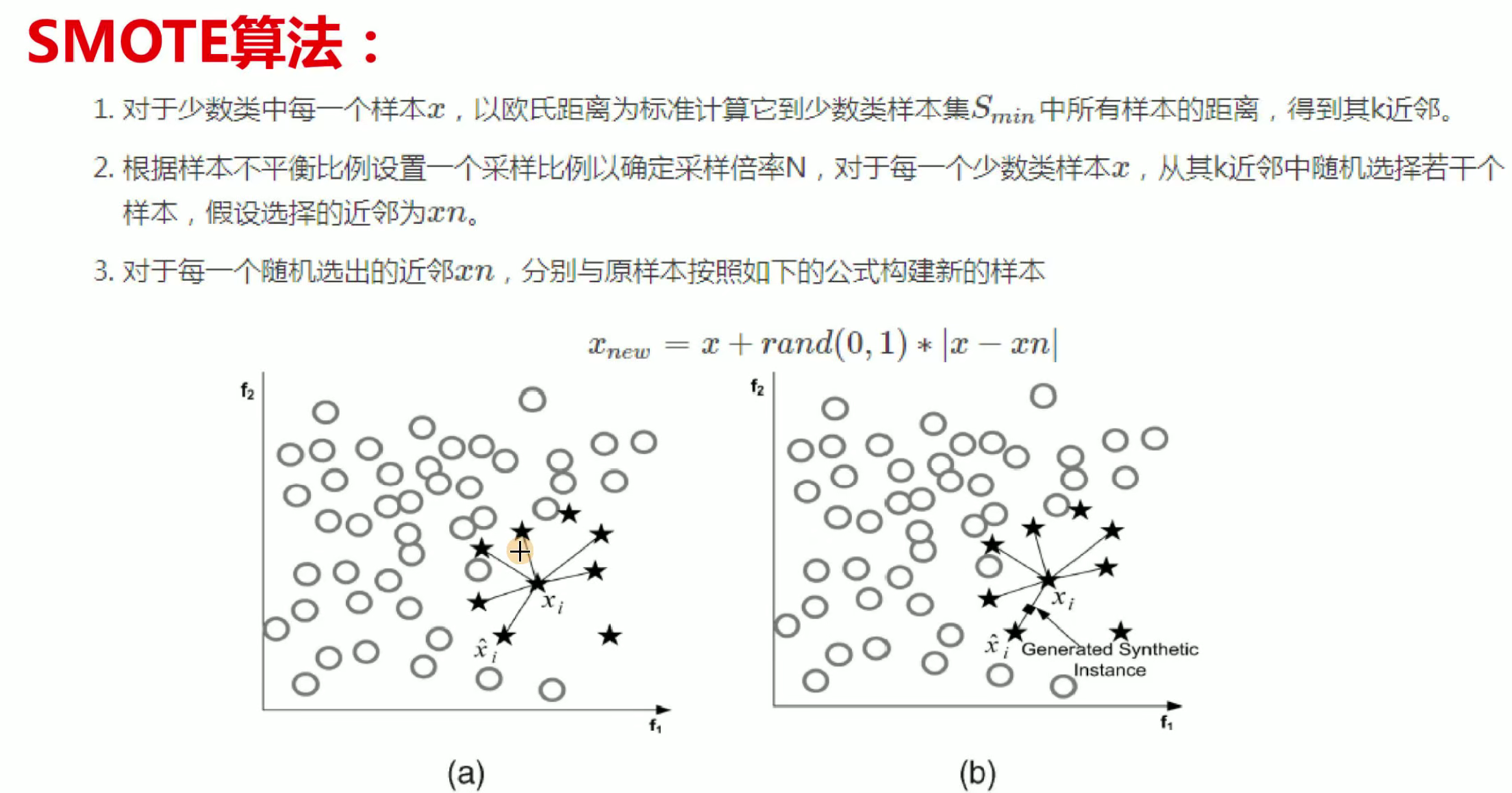
代碼部分
from imblearn.over_sampling import SMOTE#imblearn這個庫里面調用，
oversampler =SMOTE(random_state=0)#保證數據擬合效果，隨機種子
train_X, train_y = oversampler.fit_resample(train_X,train_y)#人工擬合數據?主要就是導入庫，這個庫直接pip下載就行，然后直接fit就行，這里直接導入數據，會自動識別那個多哪個少，然后進行處理。
評價方法
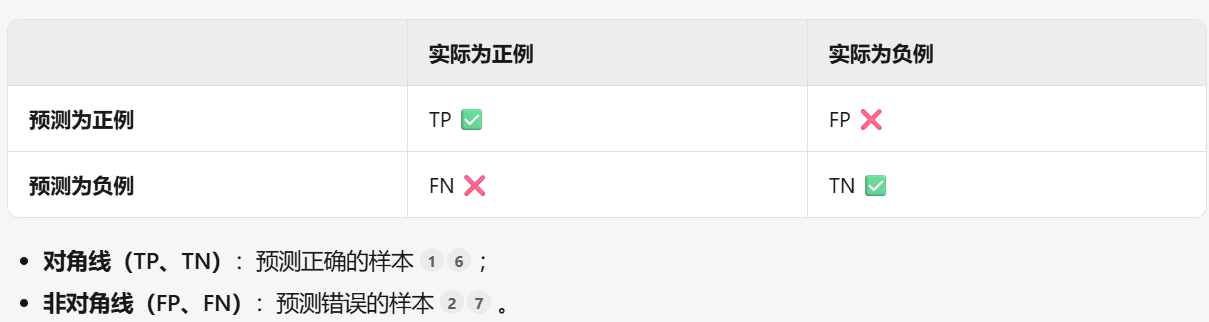
| ?指標? | ?公式? | ?適用場景? | ?特點? |
|---|---|---|---|
| ?準確率? | 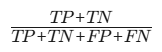 | 類別平衡數據 | 簡單直觀，但類別不平衡時失效 |
| ?精確率? | 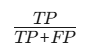 | 關注假陽性成本（如垃圾郵件檢測） | 強調預測正例的準確性 |
| ?召回率? | 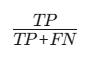 | 關注漏檢成本（如疾病診斷） | 強調捕捉正例的能力 |
| ?F1分數? |  | 平衡精確率與召回率 | 綜合性能指標，適合一般場景 |
| ?ROC-AUC? | ROC曲線下面積 | 類別不平衡或需調整閾值時 | 反映模型整體排序能力，與閾值無關 |
| ?混淆矩陣? | 四格表（TP, FP, FN, TN） | 分析錯誤類型分布 | 可視化分類細節，衍生多指標 |
