對于沒有特征或者說需要尋找另類關系的數據集，我們通常會用聚合或KNN近鄰的方法來分類，但這樣的分類或許在結果上是好的，但是解釋性并不好，有時候我們甚至能看到好的結果反直覺；而決策樹回歸做出的結果，由于其樹的結構，我們能看到每一步的決策，也就能推測出樹這么做的原因，還能進一步地調整樹的深度，使得結果更好。

以下是一個例子：

#?加載必要的包
library(rpart)??????#?決策樹
library(rpart.plot)?#?可視化樹#?1.?生成模擬數據集（非線性關系）
set.seed(123)
n?<-?200
x?<-?runif(n,?0,?10)??????????#?特征x：0到10的隨機數
y?<-?sin(x)?+?rnorm(n,?0,?0.3)?#?目標y：sin(x)加噪聲
data?<-?data.frame(x,?y)#?2.?劃分訓練集和測試集
train_idx?<-?sample(1:n,?0.7?*?n)
train_data?<-?data[train_idx,?]
test_data?<-?data[-train_idx,?]#?3.?訓練決策樹回歸模型
tree_model?<-?rpart(y?~?x,?data?=?train_data,?method?=?"anova",??#?回歸任務control?=?rpart.control(maxdepth?=?3))?#?限制樹深度#?4.?可視化樹結構
rpart.plot(tree_model,?main?=?"決策樹回歸")#?5.?預測并計算誤差
predictions?<-?predict(tree_model,?test_data)
mse?<-?mean((predictions?-?test_data$y)^2)
cat("測試集均方誤差(MSE):",?round(mse,?3),?"\n")#?6.?繪制真實值與預測值對比
plot(test_data$x,?test_data$y,?col?=?"blue",?pch?=?19,?main?=?"真實值?vs?預測值",?xlab?=?"x",?ylab?=?"y")
points(test_data$x,?predictions,?col?=?"red",?pch?=?4)
legend("topright",?legend?=?c("真實值",?"預測值"),?col?=?c("blue",?"red"),?pch?=?c(19,?4))

輸出：

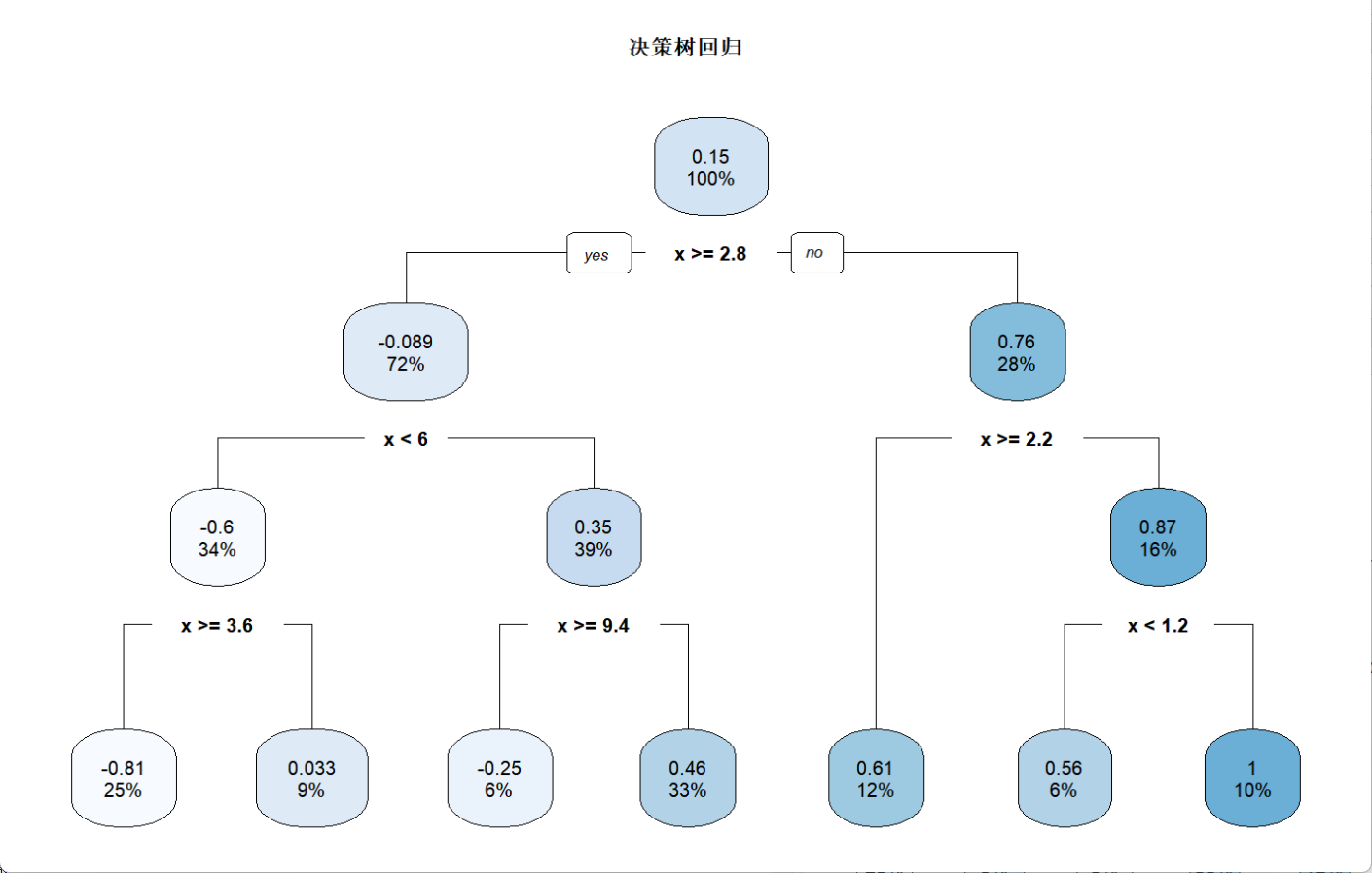
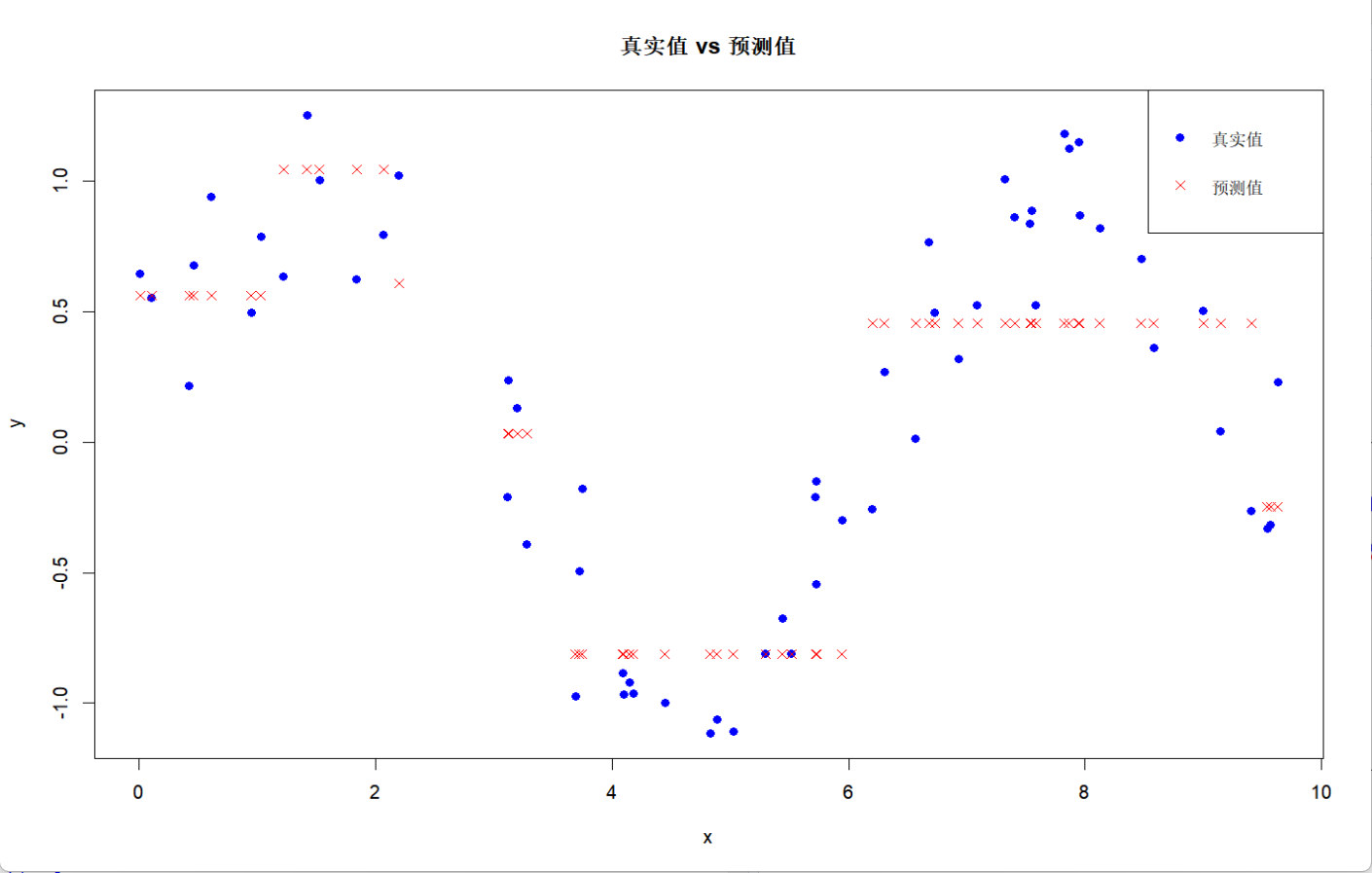
可以看到圖中的決策樹對于每一步的分支，都能看到分離之后兩邊的方差變化；而分布圖則表明決策樹對于波動較大的數據分布很難捕捉到趨勢，很容易出現欠擬合的現象，但是由于其可以根據結果反推進一步調參，反而能加深其結果的解釋性。