傅里葉變換:
運用頻域的出發點就是能夠將波形從時域變換到頻域,用傅里葉變換可以做到這一點。有如下3種傅里葉變換類型:
1.傅里葉積分(FI);
2.離散傅里葉變換(DFT);
3.快速傅里葉變換(FFT)。
傅里葉積分是一種將時域的理想數學表達變換成頻域描述的數學技術。例如,若時域中的整個波形只是一個短脈沖,就可用傅里葉積分將它變換到頻域中。
傅里葉積分是在整個時間軸上從負無窮大到正無窮大求積分,得到的結果是零頻率到正無窮大頻率上連續的頻域函數。在這個區間內,每個連續的頻率點都對應一個幅值。
實際上,時域波形是由一系列離散點組成的,且這些點是在有限的時間范圍T內測量得到的。例如,一個時鐘波形可能是從0V到1V的這樣一個信號,其周期為1ns,即頻率為1 GHz。
為了表示時鐘的一個周期,可能會用1000個離散的數據點,其中時間間隔為1ps。圖2.4所示為時域中1 GHz的時鐘波形。
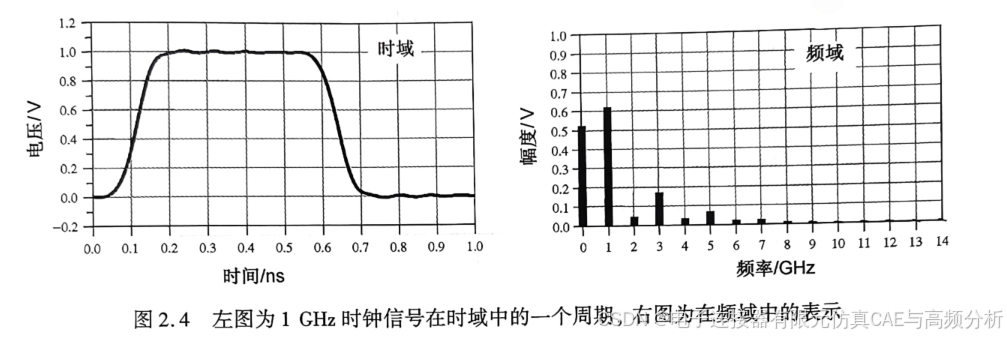
使用離散傅里葉變換可以將這個波形變換到頻域中。其中基本的假設就是原始的時域波形是周期的,它每隔T秒重復一次。與積分不同,此處只用到求和,通過簡單的數學方法就能將任意一組數據變換到頻域中。
最后就是快速傅里葉變換。除了計算每個頻率點幅度值的實際算法使用了快速矩陣代數學的技巧,它與離散傅里葉變換是完全一樣的。這種快速算法只應用于時域中的數據點個數是2的整冪次的情況,如256點512點或1024點。根據所計算電壓點個數的多少,快速傅里葉變換的計算速度比普通離散傅里葉變換可以快100~10000倍。
一般而言,工業界中常常會同時使用傅里葉積分、離散傅里葉變換和快速傅里葉變換這3種方法。現在我們知道這3種算法之間是有區別的,但同時它們又有著同樣的用途—將時域波形變換成頻域頻譜。
提示:? 在頻域中,對波形的描述變為不同頻率正弦波的集合。每個頻率分量都有相應的幅度及相位。所有這些頻率點及其幅度值的全集稱為波形的頻譜。
圖2.4所示就是一個簡單的時域波形,以及用離散傅里葉變換計算得出的頻譜圖。
每個嚴肅認真的工程師都應該至少用手工計算一次傅里葉積分來觀察它的細節。此后,就無須再手工計算了,可以使用許多商用軟件工具完成傅里葉變換,從而更快地得到答案。
許多用法相對簡單的商用軟件工具都能對輸入的任意波形進行離散傅里葉變換或快速傅里葉變換計算。SPICE軟件的每個版本都有一個稱為.FOUR指令的函數,它可以生成任一個波形前9個頻率分量的幅度。更先進的SPICE工具的大多數版本還能用離散傅里葉變換計算全套頻率點和幅度值。Microsoft Excel有FFT功能,通常可在“工程插件”中找到。






)
)




)
)




)
