本篇文章主要是講解經典的排序算法 -- 歸并排序??

---

目錄

1? 遞歸版本的歸并排序

1） 算法思想

2）?代碼?

3） 時間復雜度與空間復雜度分析?

（1） 時間復雜度

（2） 空間復雜度

2? 迭代版本的歸并排序

1） 算法思想

2） 代碼

3? 文件的歸并排序?

1） 外排序

2） 文件的歸并排序

（1） 算法思想

（2） 代碼

---

1? 遞歸版本的歸并排序

1） 算法思想

? 歸并排序與快速排序相同，都是運用了分治算法思想：將規模為 n 的問題分為k個規模較小的與原問題性質一致且相互獨立的子問題，然后解決各個子問題，將子問題的解合并為大問題的解。

? ?歸并排序是利用了之前合并兩個有序鏈表的思想，每次將大問題二分，直到分到只有一個元素的子數組的情況，將只含有一個元素的子數組看作是一個有序的子數組，然后再合并兩個有序數組，這樣子問題就解決了，解決每一個子問題之后，大問題也就隨之解決了。下面是解決兩個個子問題的算法過程（這里假設排升序）：

a. 首先定義 4 個整型變量 begin1, end1, begin2, end2, 這里假設要排序的整個數組為 arr，其中一個子問題，也就是要合并的第一個有序數組為 arr1；另一個子問題，也就是要合并的第二個有序數組為 arr2。begin1 與 begin2?分別指向 arr1 和 arr2 的起始下標，end1 與 end2 分別指向 arr1 和 arr2 的結束下標，合并兩個有序數組還需要一個中間數組 tmp 以及一個整型變量 index，tmp 來暫時存儲合并兩個有序數組后的結果，index 用來表示 tmp 數組當前存儲結果的下標。

b. 然后依次比較 arr1[begin1] 與 arr2[begin2] 的大小關系，如果 arr1[begin1] < arr2[begin2] ，那就讓 tmp[index] = arr1[begin1]，然后 ++index，++begin1；否則，就讓 tmp[index] = arr2[begin2]，然后 ++index，++begin2。循環上述過程，直到 begin1 > end1 或者 begin2 > end2。

c. 經歷過第二步之后，arr1 與 arr2 肯定會有一個數組還有元素，我們需要把剩下的元素也放到 tmp 里面，所以如果 begin1 <= end1，就讓 tmp[index] = arr1[begin1]，然后 ++index，++begin1；如果 begin2 <= end2，就讓 tmp[index] = arr2[begin2]，然后 ++index，++begin2。

d. 經歷過上述兩步之后，arr1 與 arr2 的合并結果已經放到 tmp 數組中了，最后不要忘記讓合并后的結果，也就是 tmp 中的元素要放回排序的數組 arr 中。

?下面是合并合并兩個有序數組的過程：

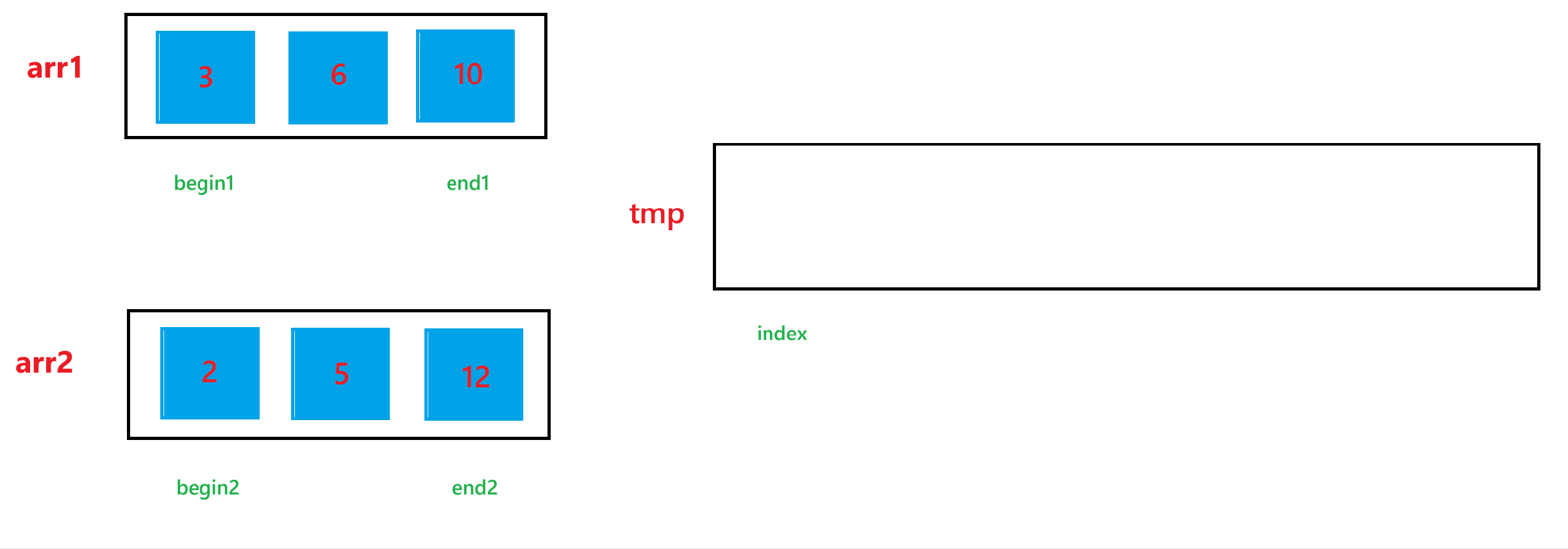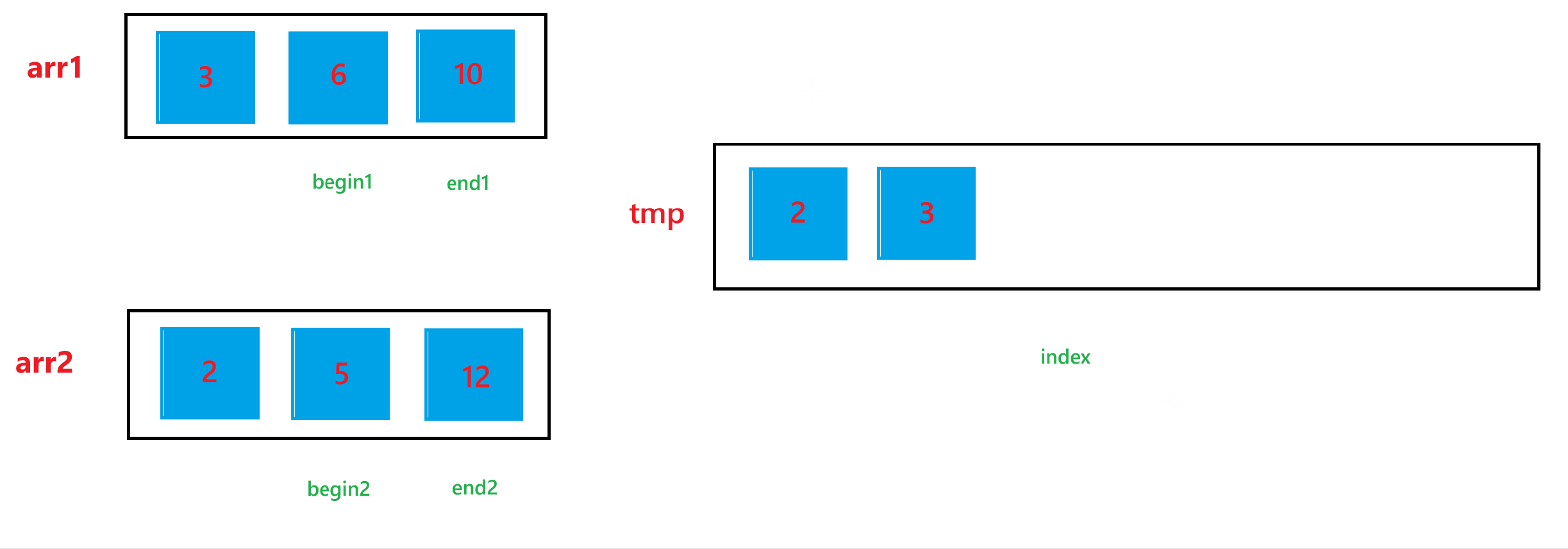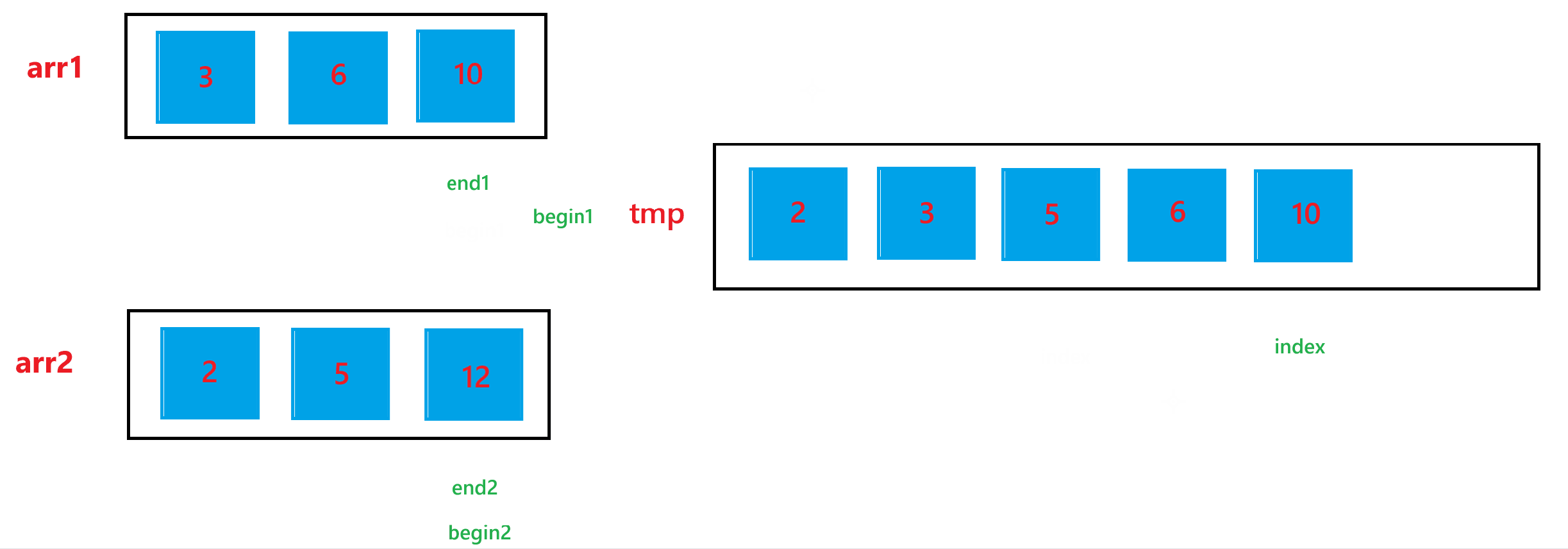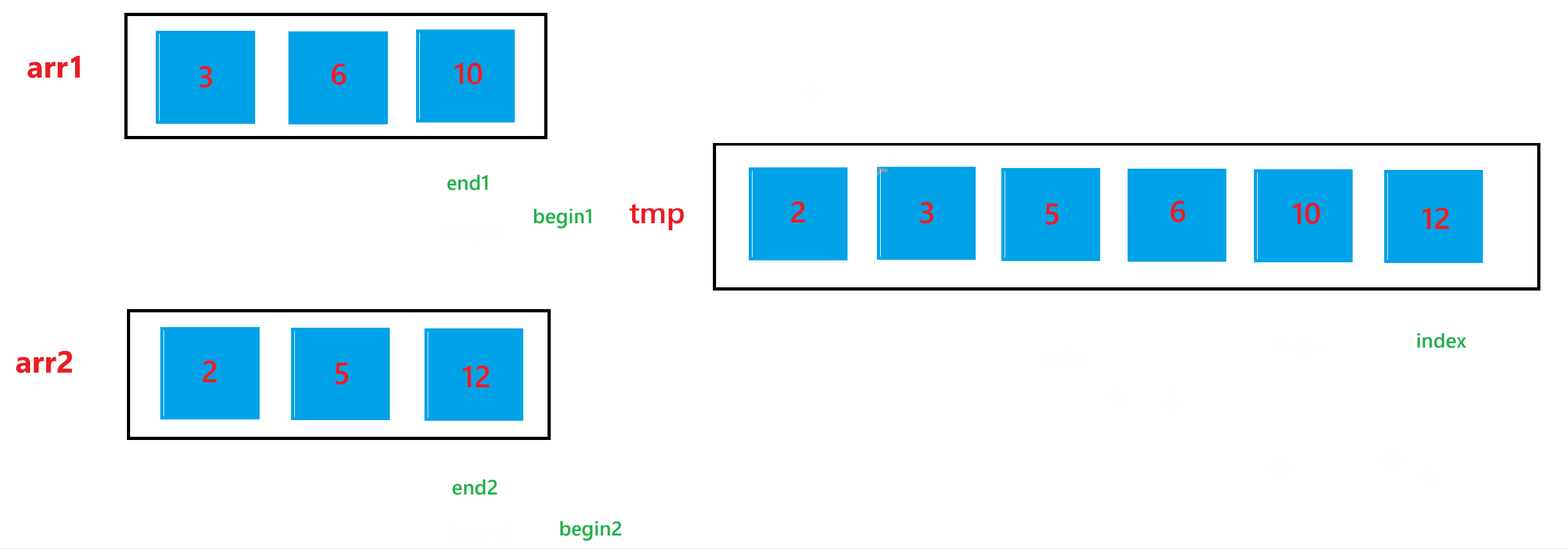
下面是歸并排序劃分子問題的過程：

注意上述過程只是描述了遞歸劃分子問題的過程，沒有進行合并，原則上是當劃分到每一條綠色的豎線左右兩邊子數組只有一個元素的時候，就應該進行合并了。

---

2）?代碼?

歸并排序主函數：

void MergeSort(int* arr,int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail！\n");exit(1);}_MergeSort(arr, 0, n - 1, tmp);free(tmp);tmp = NULL;
}

歸并排序子函數：?

void _MergeSort(int* arr, int left, int right, int* tmp)
{if (left >= right){return;}int mid = left + (right - left) / 2;_MergeSort(arr, left, mid, tmp);_MergeSort(arr, mid + 1, right, tmp);//合并兩個有序數組int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int index = left;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2])tmp[index++] = arr[begin1++];elsetmp[index++] = arr[begin2++];}while (begin1 <= end1)tmp[index++] = arr[begin1++];while (begin2 <= end2)tmp[index++] = arr[begin2++];//再將tmp數組的內容放回arr數組for (int i = left;i <= right;i++)arr[i] = tmp[i];
}

解釋： 歸并排序主函數的作用主要是動態開辟一個輔助數組 tmp 與釋放動態開辟的空間，防止內存泄漏，tmp 主要用來幫助完成有序數組的合并；在子函數里面，left 代表要進行排序的子數組的最左邊元素的下標，right 代表要進行排序的子數組的最右邊元素的下標；然后開始有一個遞歸的邊界條件，當 left >= right，也就是子數組中只有一個元素或者沒有元素的時候，就會停止遞歸，此時將只有一個元素的子數組視為是一個有序數組；邊界條件下面的三行代碼主要就是用來進行遞歸，劃分子問題的，首先計算出大問題的中間位置下標 mid，然后將大問題在中間數組劃分為兩個子問題，也就是對 [left, mid] 與 [mid + 1, right] 區間的數組進行遞歸；再后面的代碼就是為了解決某兩個具體的子問題也就是合并兩個有序數組的過程（上面已經講解過，這里不再贅述）。

?測試用例：

int main()
{int arr[] = { 10, 2, 5, 7, 1, 4, 8, 9, 6, 20};int n = sizeof(arr) / sizeof(arr[0]);MergeSort(arr, n);Print(arr, n);return 0;
}

---

3） 時間復雜度與空間復雜度分析?

（1） 時間復雜度

? 與快速排序相同，帶有遞歸的函數的時間復雜度計算包括兩部分，一部分是解決子問題的時間復雜度，另一部分是遞歸的深度，T(n) = 遞歸深度 * 解決子問題的時間復雜度。

? 我們先來看解決子問題的時間復雜度，看上面解決具體解決子問題的代碼，由于只有一層循環，且循環的次數最多是 end1 - begin1 或者 end2 - begin2 次，最壞情況下是對最開始要排序的整個數組從中間劃分的兩個子數組進行排序的時候，此時循環的次數就是 n / 2 次，所以解決子問題的時間復雜度 T(n) = O(n)。

? 再來看遞歸的深度，由于每次都對數組進行二分，在中間位置劃分數組，對左邊數組進行遞歸，再對右邊數組進行遞歸，所以遞歸樹應該為：

我們假設最開始的數組元素個數為 n，那么遞歸到第二層的時候每個子數組元素個數就為 n/2，第三層就為 n/4，也就是 n/2^2，第四層就是 n/2^3，所以遞歸到第 x 層的時候元素個數就為 n/2^x，而遞歸的停止條件為元素個數為 1，所以 n/2^x = 1? ==>? x = ，所以總的層數應該是??+ 1 層，所以遞歸的深度為??+ 1。

? 所以歸并排序的時間復雜度 T(n) = O(nlogn + n)? ==>? T(n) = O(nlogn)。

（2） 空間復雜度

? 由于在函數中使用了一個輔助數組 tmp 來幫助合并，其余都是有限的變量，所以空間復雜度?S(n) = O(n)。

---

2? 迭代版本的歸并排序

1） 算法思想

? 在迭代版本的歸并排序中，我們依然可以借助遞歸版本歸并排序的算法思想：先將數組劃分到 1 個元素的子數組的情況，將 1 個元素的子數組看作是有序的數組，然后依次合并兩個有序數組，最終使數組有序；在迭代版本歸并排序中，我們劃分子問題是用一個 gap 變量來實現的，具體過程如下：

a. 函數會傳入兩個參數：arr（數組元素首地址）與 n （數組元素個數），先創建一個整型變量 gap 與一個輔助數組 tmp（用來合并兩個有序數組）；開始先讓 gap = 1，代表每個要合并的數組里只有一個元素，之后每次循環都讓 gap *= 2，代表要合并的數組由 1 個元素變為 2 個元素，之后再變為 4 個元素，依次類推，直到?gap >= n，就停止排序。

b. 然后在每次循環里面，由于在大數組里我們要尋找要合并的兩個子數組，所以我們還要用一個變量 i 來遍歷數組，尋找要合并的兩個子數組；在循環過程中，i 每次會指向要合并的兩個子數組中第一個子數組的首元素，由于每次首次要合并的第一個子數組總是以 0 下標元素開頭的子數組，所以 i 總是以 0 開頭，然后合并完兩個有序子數組之后，i 會指向下一次要合并的兩個有序子數組的第一個子數組首元素，所以 i 在遍歷過程中會跳過上一次排序的兩個子數組，也就是 2 * gap 個元素，即 i += 2 * gap；停止條件也很簡單，就是 i >= n 越界時，就會停止兩個子數組的合并。

c. 在合并兩個子數組的過程中需要找到兩個子數組，這里用 begin1, end1 代表第一個要合并的子數組的起始和結束位置，begin2 和 end2 代表第二個要合并的子數組的起始和結束位置，根據 i 與 gap 就可以推算出 begin1、end1、begin2、與 end2：begin1 = i，end1 = i + gap - 1，begin2 = i + gap，end2 = begin1 + gap - 1 = i + 2 * gap - 1。

d. 再創建一個?index 來記錄要放到 tmp 數組中的位置，開始先讓 index = begin1，之后進行兩個有序數組的合并（上面遞歸版本講解過，這里不再贅述），最后不要忘記讓 tmp 中的元素放到 arr 數組中。

?當 gap = 1 時排序過程如圖所示：?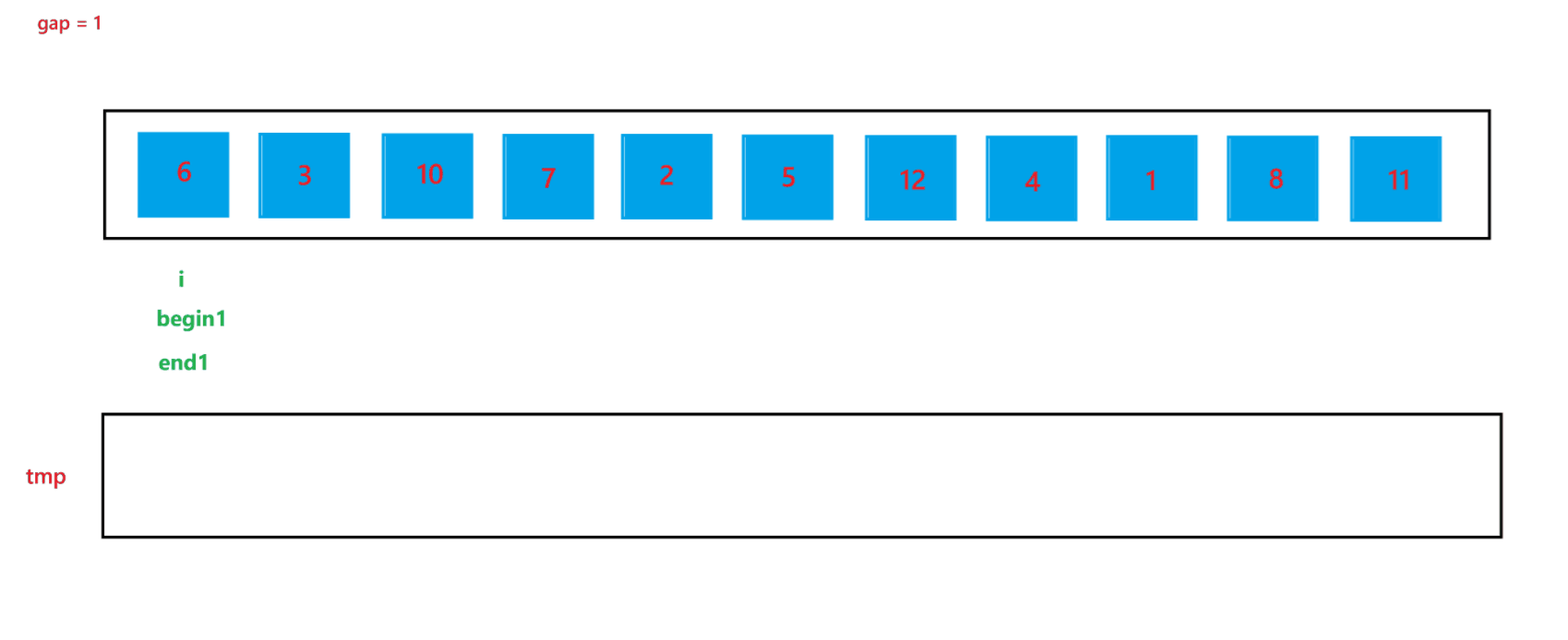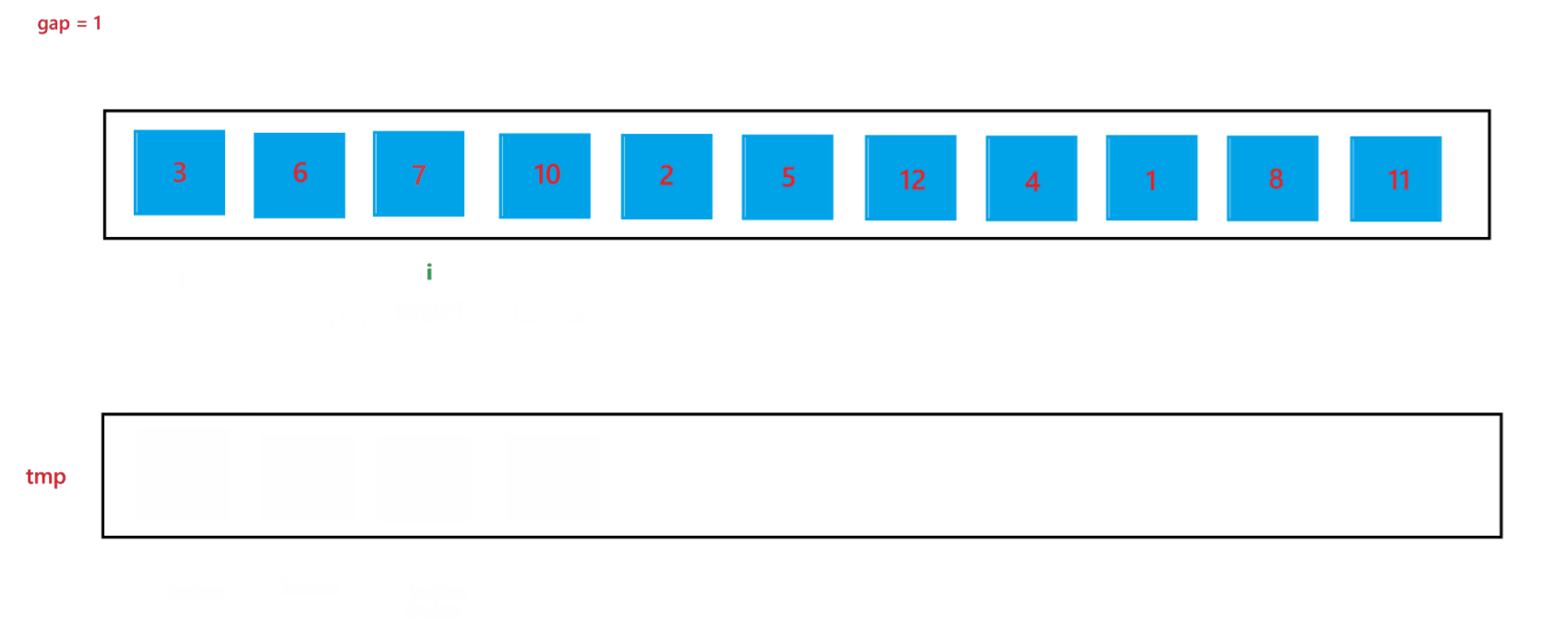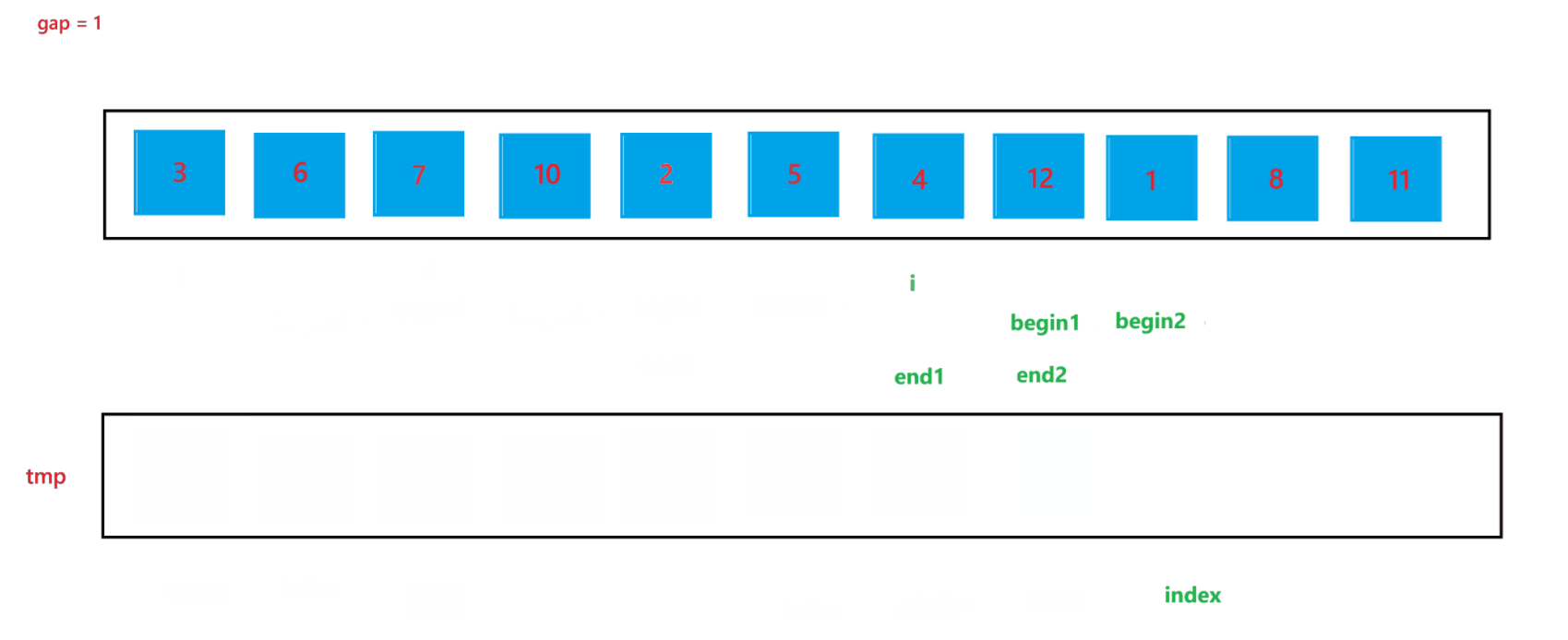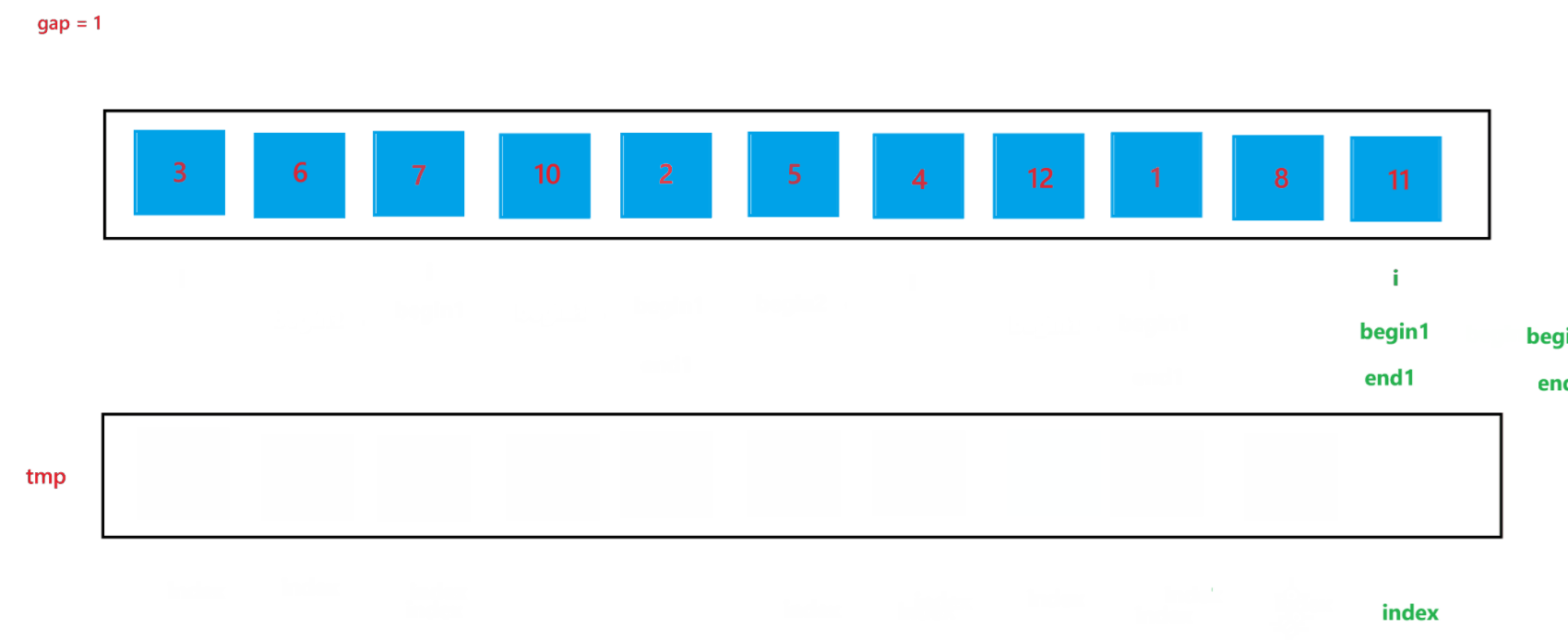

在上述的合并過程中，我們可以發現 begin2 與 end2 是可能發生越界的，所以當發生越界情況時，我們需要特殊處理一下：當 begin2 越界時，此時代表 begin1 的子數組后面是沒有 begin2 子數組與其合并的，也就是此時只有一個有序子數組，就代表此次不需要合并了，跳出循環即可；當end2 越界時，會在 gap = 2 中出現，下面我們再詳細討論。?

?當 gap = 2?時排序過程如圖所示：

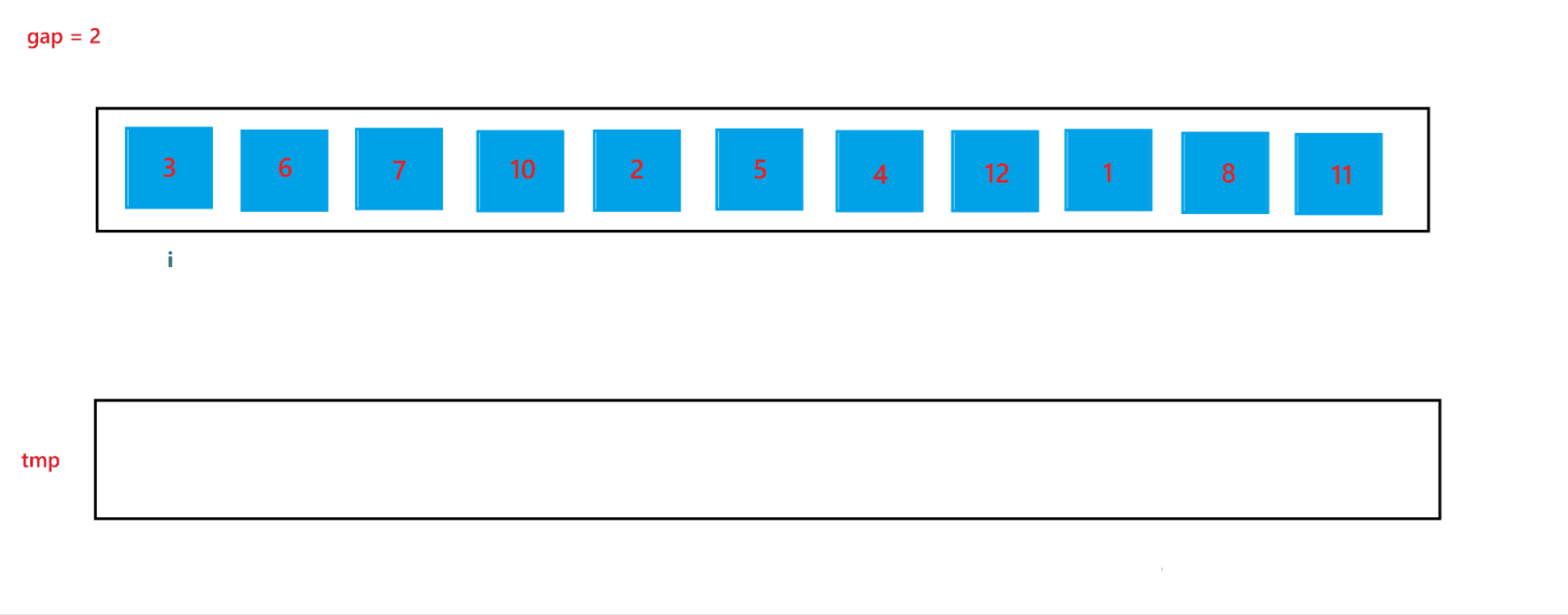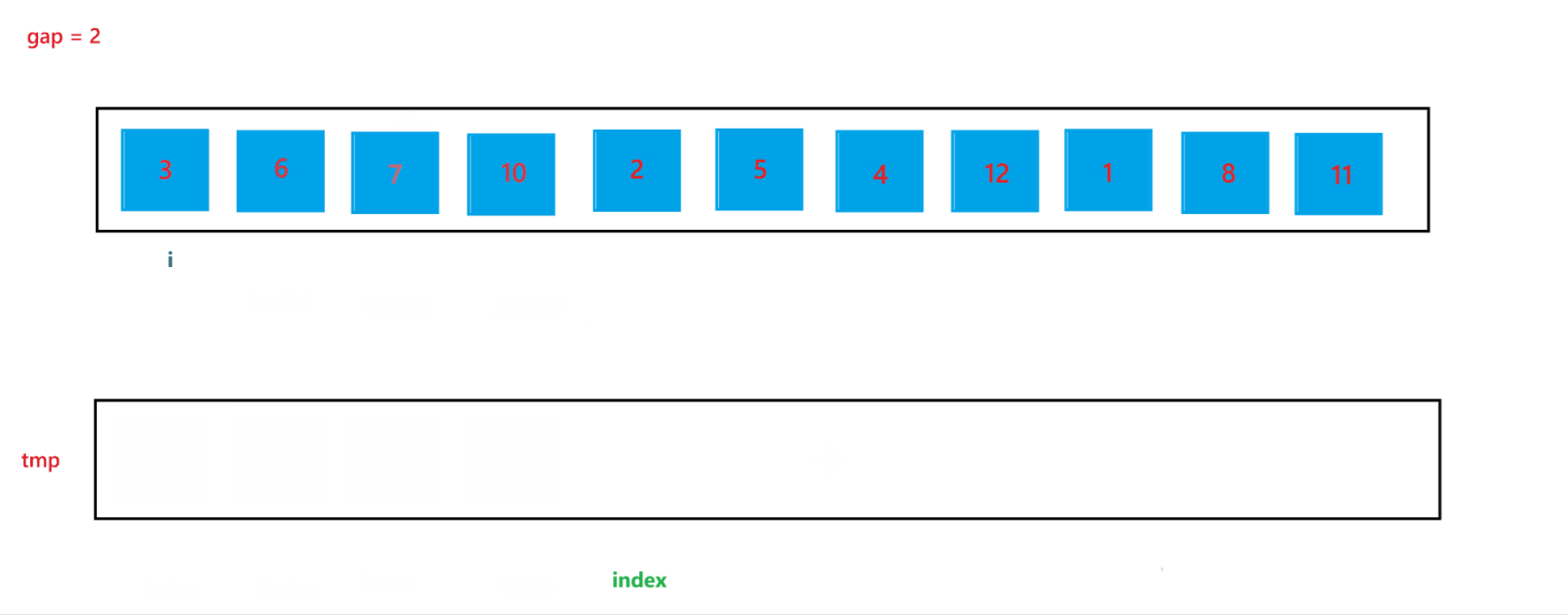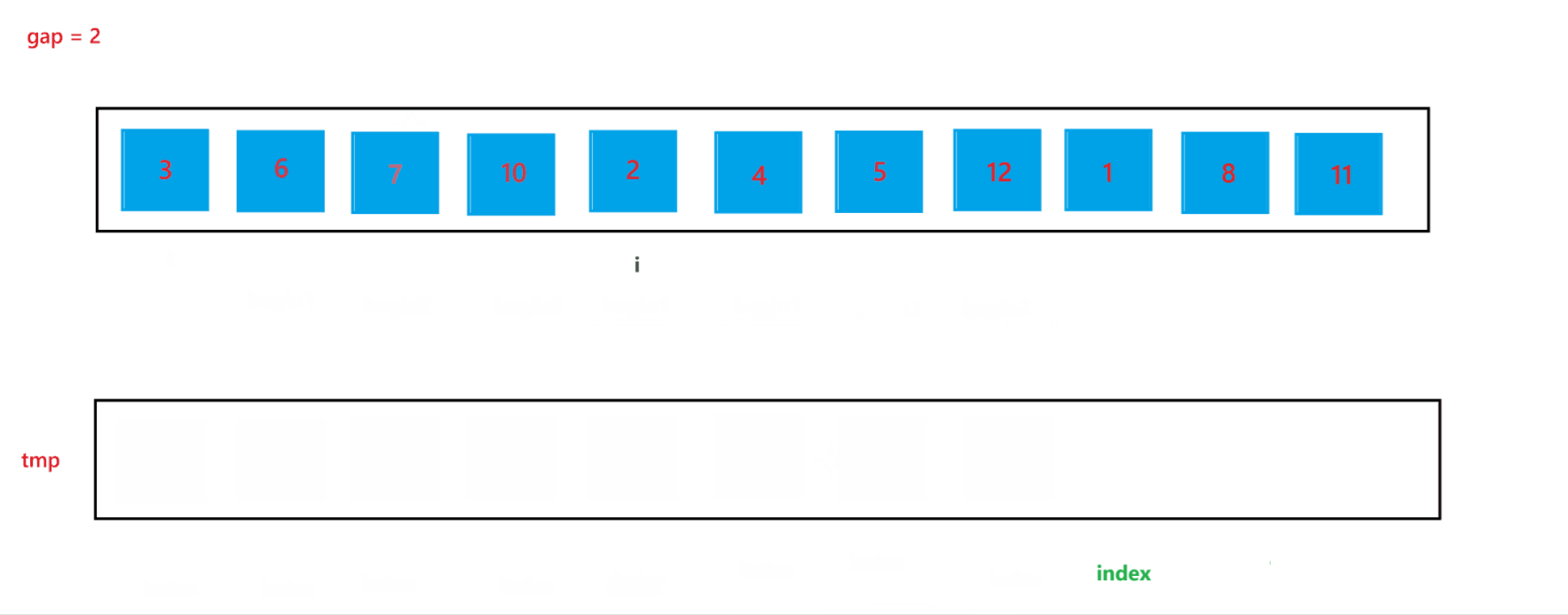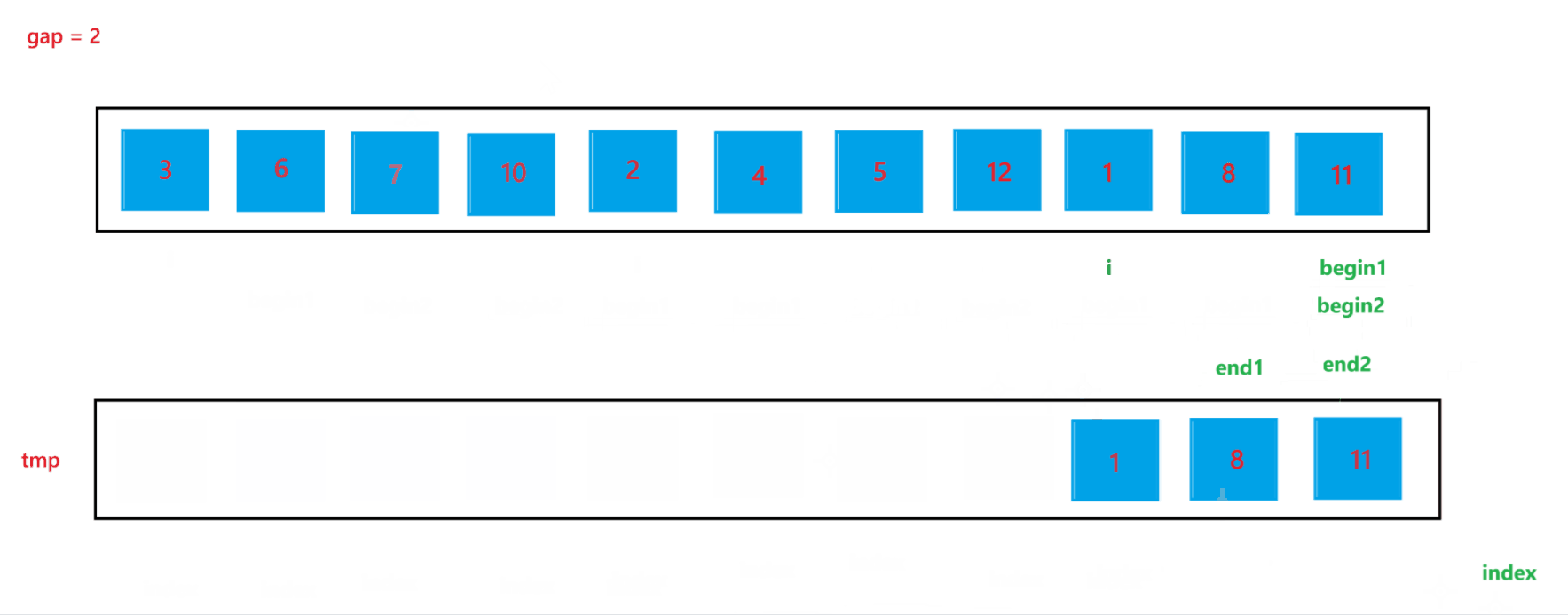
通過上述合并過程，可以看到當 end2 出現越界行為時，我們讓其回到了最后一個位置，也就是 end2 = n - 1，此時就可以避免越界行為的發生。

? 接下來 gap 會繼續 gap *= 2，變為4，之后會再變為 8，最后變為 16 的時候由于大于 n，會退出循環，排序就完成了，如果你有興趣可以自己畫一下圖模擬一下過程，在這里就不再畫圖。

---

2） 代碼

void MergeSortNorR(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail！\n");exit(1);}//每組元素的個數int gap = 1;while (gap < n){//遍歷每兩組，進行兩組之間的合并// i 每次指向要合并兩組的第一組的第一個元素for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int index = begin1;//為了防止要合并第二個數組越界，需要特殊處理一下//begin2 如果越界，代表第一組沒有要合并的第二組了，不用合并了，直接跳出循環if (begin2 >= n){break;}//如果要合并的第二組元素不滿gap個，那就有多少合并多少if (end2 >= n){end2 = n - 1;}//合并兩個有序數組while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else{tmp[index++] = arr[begin2++];}}while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}//把tmp中的數據放回原數組memcpy(arr + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}//最后不要忘記釋放tmp數組free(tmp);tmp = NULL;
}

測試用例：

#include<stdio.h>
#include<stdlib.h>void MergeSortNorR_Test()
{//奇數個元素的情況//int arr[] = { 2, 1, 10, 4, 7, 3, 8, 5, 11 };//偶數個元素的情況int arr[] = { 2, 1, 10, 4, 7, 3, 8, 5 };int n = sizeof(arr) / sizeof(arr[0]);MergeSortNorR(arr, n);for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}int main()
{MergeSortNorR_Test();return 0;
}

---

3? 文件的歸并排序?

1） 外排序

? ? ? ? 不同于內排序，外排序是進行文件與磁盤內數據的排序，也就是不是直接對存儲在內存中的數據進行排序，而是先將外存中的數據先調入內存，排完序之后再將數據放回文件或者磁盤中，就是外排序。

? ? ? ? 那么什么時候會用到外排序呢？一般都是數據量很多時，比如一個文件里面有 10G 的數據，無法全部調入內存，還想要對文件內的數據進行排序，此時就需要進行外排序。

2） 文件的歸并排序

（1） 算法思想

? ? ? ? 如果想要排序的數據量較大時，我們一般都會先把數據保存在文件中，然后通過 C 語言中文件的相關操作，將文件中的數據排序好后，再放入文件之中，而在七大排序算法中，不需要內存的隨機訪問而又效率比較快的排序算法就是歸并排序了（堆排序、快速排序、希爾排序都需要對內存中的數據進行隨機訪問），所以歸并排序算法既可以用于實現內排序，也可以實現外排序，以下是對文件進行歸并排序的算法過程：

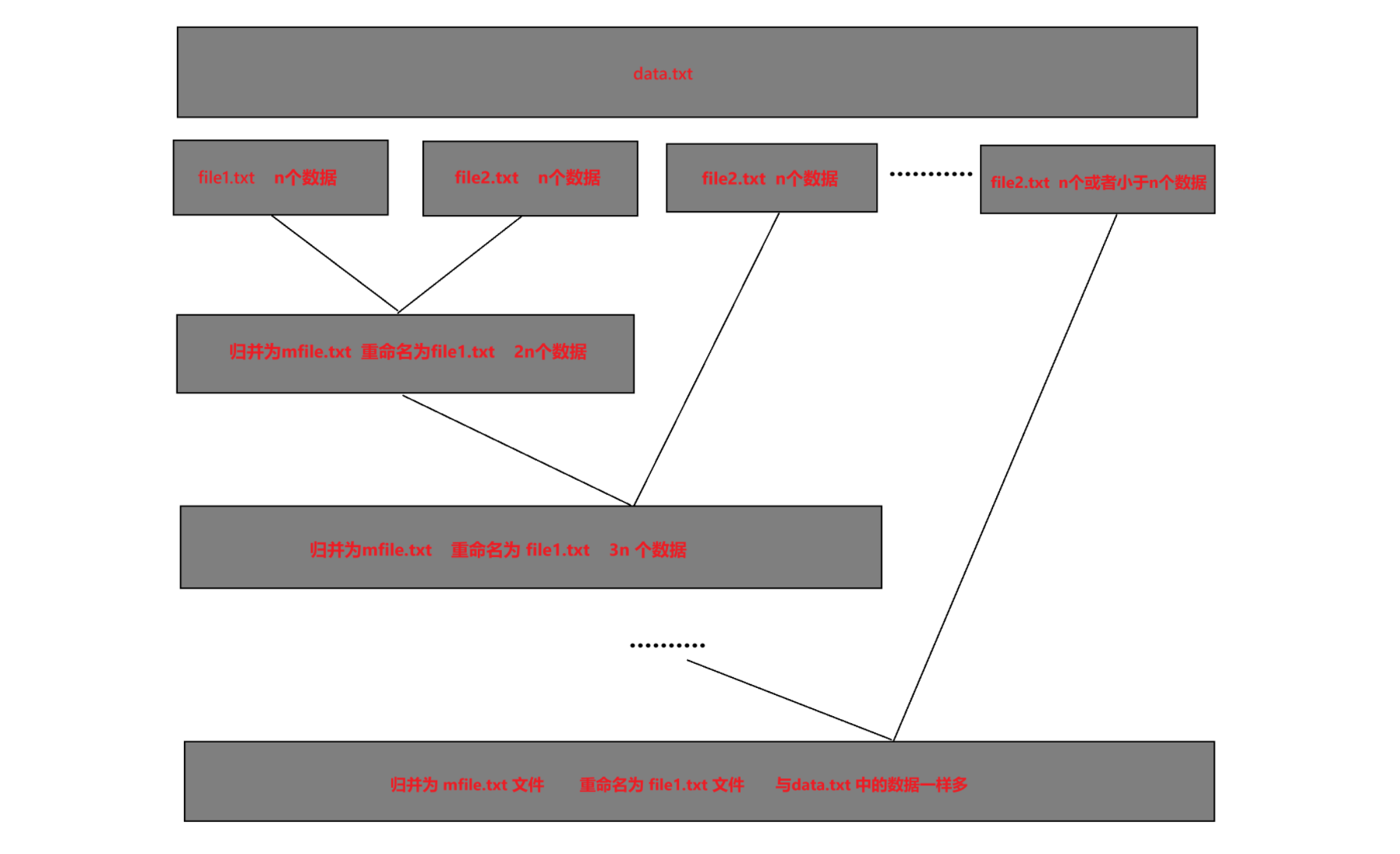
a. 先在要進行排序的文件 data.txt 中取出 n?個數據，將這 n 個數據排好序后，放到 file1.txt 里面；再取出 n 個數據，排好序之后，放到 file2.txt 文件里面。

b. 然后對 file1.txt 和 file2.txt 中的數據進行歸并（就是前面歸并排序中合并兩個有序子數組的過程），將歸并后的數據放到 mfile.txt 里面。

c. 此時，file1.txt 與 file2.txt 已經沒用了，刪除 file1,txt 與 file2.txt 文件，將 mfile.txt 文件重命名為 file1.txt 文件。

d. 然后再取出 n 個數據放到 file2.txt 里面，再將 file1.txt（之前的 mfile.txt 文件）與 file2.txt 文件歸并，將歸并后的數據放到新的 mfile.txt 文件里面；如此循環，直到 data.txt 文件中沒有數據為止。最終，排好序的數據會存儲在 file1.txt 文件里面。

上述算法過程如下圖所示：
?

? ? ? ? 在上述算法思想的實現過程中，有三個函數需要我們了解一下，第一個就是刪除文件的函數，第二個就是對文件名重命名的函數，還有一個就是對數據進行排序的函數，接下來我們來一次了解一下。

a.? 刪除文件的函數：

刪除文件的函數的函數名字叫做 remove 函數，與 printf 和 scanf 函數相同，其都被包含在 stdio.h 頭文件下，傳入的參數僅有一個，就是要刪除文件的文件名字符指針即可。所以刪除 file1.txt 文件與 file2.txt 文件，我們可以直接 remove("file1.txt") 與 remove("file2.txt")。

?b. 重命名的函數：

對文件進行重命名的函數叫做 rename 函數，傳入的參數也很簡單，第一個參數為要修改的文件的文件名的字符指針，也就是 oldname，第二個參數為修改后的文件名的字符指針，也就是 newname。所以將 mfile 重命名為 file1.txt 可以寫為 rename("mfile.txt", "file1.txt")。

c. 對數據進行排序的函數：這里可以使用我們之前學習過的七大排序算法，比如：快速排序、堆排序、希爾排序都可以，當然這里也可以直接使用 qsort 函數：

可以看到 qsort 函數是需要四個參數的，第一個是需要進行排序的首元素的指針，第二個參數是進行排序的元素的個數，第三個參數是需要進行排序的元素的大小（單位為字節），第四個參數是一個函數指針，其指向的函數的返回值為 int, 兩個參數類型為 const void*。對于第四個參數 compare 我們具體講解一下：

從下面的表格我們可以看出其對返回值是有要求的，如果第一個參數想排在第二個參數之前，那就返回小于 0 的數字；如果相等返回 0；否則返回大于 0 的數字，由于我們這里排的都是整形，且升序排序，所以我們可以這樣設計 compare 函數：

int compare(const void* a, const void* b)
{return (*(int*)a - *(int*)b);
}

?注意，一定要對 a 和 b 進行強轉，因為 void* 類型的指針無法進行解引用的。

---

（2） 代碼

#include<stdio.h>
#include<stdlib.h>
#include<time.h>void CreateData()
{const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen fail！\n");exit(1);}srand(time(0));const int n = 1000000;for (int i = 0; i < n; i++){fprintf(fin, "%d\n", rand() + i);}fclose(fin);
}int Compare(const void* a, const void* b)
{return (*(int*)a - *(int*)b);
}//返回讀取到的數據個數
int SortNValeToFile(FILE* fout, int n, const char* file)
{int x = 0;int* a = (int*)malloc(sizeof(int) * n);if (a == NULL){perror("malloc error");return 0;}// 想讀取n個數據，如果遇到文件結束，應該讀到j個int j = 0;for (int i = 0; i < n; i++){if (fscanf(fout, "%d", &x) == EOF)break;a[j++] = x;}if (j == 0){free(a);return 0;}// 排序qsort(a, j, sizeof(int), Compare);FILE* fin = fopen(file, "w");if (fin == NULL){free(a);perror("fopen error");return 0;}// 寫回file1文件for (int i = 0; i < j; i++){fprintf(fin, "%d\n", a[i]);}free(a);fclose(fin);return j;
}void MergeFile(const char* file1, const char* file2, const char* mfile)
{FILE* fout1 = fopen(file1, "r");if (fout1 == NULL){perror("fopen1 fail！\n");return;}FILE* fout2 = fopen(file2, "r");if (fout2 == NULL){perror("fopen2 fail！\n");return;}FILE* fin = fopen(mfile, "w");if (fin == NULL){perror("fin fail！\n");return;}//對文件進行歸并排序int x1 = 0;int x2 = 0;int ret1 = fscanf(fout1, "%d", &x1);int ret2 = fscanf(fout2, "%d", &x2);while (ret1 != EOF && ret2 != EOF){//如果 file1 的數據小于 file2 的數據，就將 file1 的數放到 mfile 里面if (x1 < x2){fprintf(fin, "%d\n", x1);ret1 = fscanf(fout1, "%d", &x1);}else{fprintf(fin, "%d\n", x2);ret2 = fscanf(fout2, "%d", &x2);}}while (ret1 != EOF){fprintf(fin, "%d\n", x1);ret1 = fscanf(fout1, "%d", &x1);}while (ret2 != EOF){fprintf(fin, "%d\n", x2);ret2 = fscanf(fout2, "%d", &x2);}fclose(fout1);fclose(fout2);fclose(fin);
}int main()
{CreateData();//創建三個文件const char* file1 = "file1.txt";const char* file2 = "file2.txt";const char* mfile = "mfile.txt";//從data.txt中取出n個數據放到file1與file2中FILE* fout = fopen("data.txt", "r");if (fout == NULL){perror("fopen fail！\n");exit(1);}int N = 100000;SortNValeToFile(fout, N, file1);SortNValeToFile(fout, N, file2);while (1){//將兩個文件歸并到 mfile 文件MergeFile(file1, file2, mfile);//刪除file1 與 file2 文件remove(file1);remove(file2);//將mfile 重命名為 file1rename(mfile, file1);//再從data.txt中取出n個數據放到file2 里面//如果取不到數據說明歸并結束if (SortNValeToFile(fout, N, file2) == 0)break;}return 0;
}