4月22日復盤-開始卷積神經網絡

4月24日復盤

一、CNN

視覺處理三大任務：圖像分類、目標檢測、圖像分割

上游：提取特征，CNN

下游：分類、目標、分割等，具體的業務

1. 概述

? 卷積神經網絡是深度學習在計算機視覺領域的突破性成果。在計算機視覺領域, 往往我們輸入的圖像都很大，使用全連接網絡的話，計算的代價較高。另外圖像也很難保留原有的特征，導致圖像處理的準確率不高。

? 卷積神經網絡（Convolutional Neural Network，CNN）是一種專門用于處理具有網格狀結構數據的深度學習模型。最初，CNN主要應用于計算機視覺任務，但它的成功啟發了在其他領域應用，如自然語言處理等。

? 卷積神經網絡（Convolutional Neural Network）是含有卷積層的神經網絡. 卷積層的作用就是用來自動學習、提取圖像的特征。

? CNN網絡主要有三部分構成：卷積層、池化層和全連接層構成，其中卷積層負責提取圖像中的局部特征；池化層用來大幅降低運算量并特征增強；全連接層類似神經網絡的部分，用來輸出想要的結果。

1.1 使用場景

外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳

在這里插入圖片描述

1.2 與傳統網絡的區別

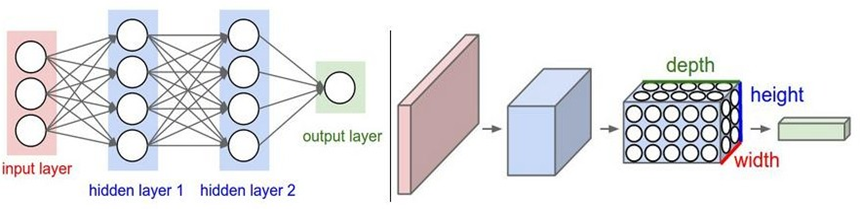
在這里插入圖片描述

1.3 全連接的局限性

全連接神經網絡并不太適合處理圖像數據…

1.3.1 參數量巨大

$\times W^T + b$

全連接結構計算量非常大，假設我們有1000×1000的輸入，如果隱藏層也是1000×1000大小的神經元，由于神經元和圖像每一個像素連接，則參數量會達到驚人的1000×1000×1000×1000，僅僅一層網絡就已經有 $10^{12}$ 個參數。

1.3.2 表達能力太有限

全連接神經網絡的角色只是一個分類器，如果將整個圖片直接輸入網絡，不僅參數量大，也沒有利用好圖片中像素的空間特性，增加了學習難度，降低了學習效果。

1.4 卷積思想

卷：從左往右，從上往下

積：乘積，求和

1.4.1 概念

? Convolution，輸入信息與卷積核(濾波器,Filter)的乘積。

1.4.2 局部連接

局部連接可以更好地利用圖像中的結構信息，空間距離越相近的像素其相互影響越大。
根據局部特征完成目標的可辨識性。

1.4.3 權重共享

圖像從一個局部區域學習到的信息應用到其他區域。
減少參數，降低學習難度。

2. 卷積層

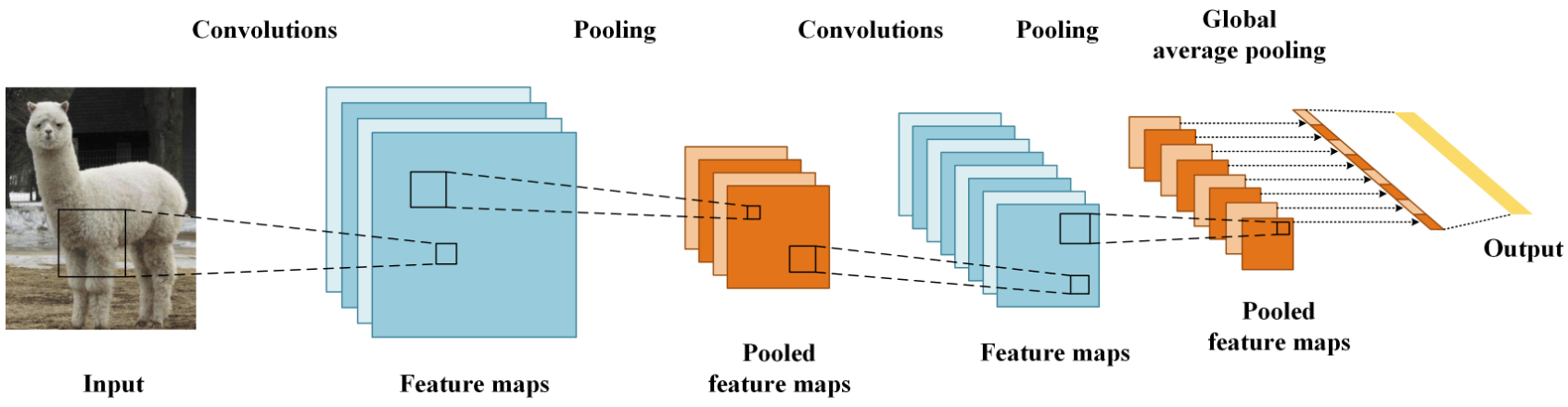
在這里插入圖片描述

接下來，我們開始學習卷積核的計算過程, 即: 卷積核是如何提取特征的。

2.1 卷積核

? 卷積核是卷積運算過程中必不可少的一個“工具”，在卷積神經網絡中，卷積核是非常重要的，它們被用來提取圖像中的特征。

卷積核其實是一個小矩陣，在定義時需要考慮以下幾方面的內容：

卷積核的個數：卷積核（過濾器）的個數決定了其輸出特征矩陣的通道數。
卷積核的值：卷積核的值是初始化好的，后續進行更新。
卷積核的大小：常見的卷積核有1×1、3×3、5×5等，一般都是奇數 × 奇數。

下圖就是一個3×3的卷積核：
在這里插入圖片描述

2.2 卷積計算

2.2.1 卷積計算過程

? 卷積的過程是將卷積核在圖像上進行滑動計算，每次滑動到一個新的位置時，卷積核和圖像進行點對點的計算，并將其求和得到一個新的值，然后將這個新的值加入到特征圖中，最終得到一個新的特征圖。

在這里插入圖片描述

input 表示輸入的圖像
filter 表示卷積核, 也叫做濾波器
input 經過 filter 的得到輸出為最右側的圖像，該圖叫做特征圖

? 那么, 它是如何進行計算的呢？卷積運算本質上就是在濾波器和輸入數據的局部區域間做點積。

在這里插入圖片描述

左上角的點計算方法：

外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳

按照上面的計算方法可以得到最終的特征圖為:

在這里插入圖片描述

? 卷積的重要性在于它可以將圖像中的特征與卷積核進行卷積操作，從而提取出圖像中的特征。

? 可以通過不斷調整卷積核的大小、卷積核的值和卷積操作的步長，可以提取出不同尺度和位置的特征。

# 面向對象的模塊化編程
from matplotlib import pyplot as plt
import os
import torch
import torch.nn as nndef test001():current_path = os.path.dirname(__file__)img_path = os.path.join(current_path, "data", "彩色.png")# 轉換為相對路徑img_path = os.path.relpath(img_path)# 使用plt讀取圖片img = plt.imread(img_path)print(img.shape)# 轉換為張量：HWC  ---> CHW  ---> NCHW  鏈式調用img = torch.tensor(img).permute(2, 0, 1).unsqueeze(0)# 創建卷積核  (501, 500, 4)conv = nn.Conv2d(in_channels=4,  # 輸入通道out_channels=32,  # 輸出通道kernel_size=(5, 3),  # 卷積核大小stride=1,  # 步長padding=0,  # 填充bias=True)# 使用卷積核對圖像進行卷積操作  [9999]  [[[[]]]]out = conv(img)# 輸出128個特征圖conv2 = nn.Conv2d(in_channels=32,  # 輸入通道out_channels=128,  # 輸出通道kernel_size=(5, 5),  # 卷積核大小stride=1,  # 步長padding=0,  # 填充bias=True)out = conv2(out)print(out)# 把圖像顯示出來print(out.shape)plt.imshow(out[0][10].detach().numpy(), cmap='gray')plt.show()# 作為主模塊執行
if __name__ == "__main__":test001()

2.2.2 卷積計算底層實現

并不是水平和垂直方向的循環。

下圖是卷積的基本運算方式：

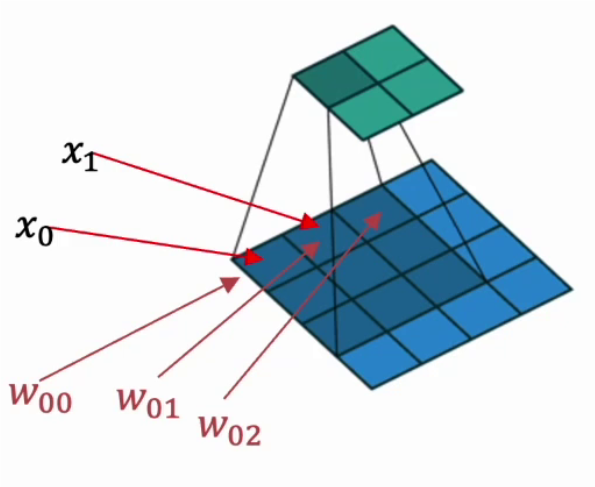
卷積真正的計算過程如下圖：

2.3 邊緣填充

? Padding

? 通過上面的卷積計算，我們發現最終的特征圖比原始圖像要小，如果想要保持圖像大小不變, 可在原圖周圍添加padding來實現。

? 更重要的，邊緣填充還更好的保護了圖像邊緣數據的特征。

在這里插入圖片描述

2.4 步長Stride

按照步長為1來移動卷積核，計算特征圖如下所示：

在這里插入圖片描述

如果我們把 Stride 增大為2，也是可以提取特征圖的，如下圖所示：

在這里插入圖片描述

stride太小：重復計算較多，計算量大，訓練效率降低；
stride太大：會造成信息遺漏，無法有效提煉數據背后的特征；

2.5 多通道卷積計算

首先我們需要認識下通道，做到顆粒度對齊~

2.5.1 數字圖像的標識

我們知道圖像在計算機眼中是一個矩陣

在這里插入圖片描述

通道越多，可以表達的特征就越豐富~

2.5.2 具體計算實現

實際中的圖像都是多個通道組成的，我們怎么計算卷積呢？

在這里插入圖片描述

計算方法如下：

當輸入有多個通道(Channel), 例如RGB三通道, 此時要求卷積核需要有相同的通道數。
卷積核通道與對應的輸入圖像通道進行卷積。
將每個通道的卷積結果按位相加得到最終的特征圖。

如下圖所示:

在這里插入圖片描述

2.6 多卷積核卷積計算

? 實際對圖像進行特征提取時, 我們需要使用多個卷積核進行特征提取。這個多個卷積核可以理解為從不同到的視角、不同的角度對圖像特征進行提取。

? 那么, 當使用多個卷積核時, 應該怎么進行特征提取呢?

在這里插入圖片描述

2.7 特征圖大小

輸出特征圖的大小與以下參數息息相關:

size: 卷積核/過濾器大小，一般會選擇為奇數，比如有 1×1, 3×3， 5×5
Padding: 零填充的方式
Stride: 步長

那計算方法如下圖所示:
在這里插入圖片描述

輸入圖像大小: W x W
卷積核大小: F x F
Stride: S
Padding: P
輸出圖像大小: N x N

以下圖為例:

圖像大小: 5 x 5
卷積核大小: 3 x 3
Stride: 1
Padding: 1
(5 - 3 + 2) / 1 + 1 = 5, 即得到的特征圖大小為: 5 x 5

在這里插入圖片描述

2.8 只卷一次？

在這里插入圖片描述

2.9 卷積參數共享

? 數據是 $32 \times 32 \times 3$ 的圖像，用 $10$ 個 $5 \times 5$ 的filter來進行卷積操作，所需的權重參數有多少個呢？

$5 \times 5 \times 3 = 75$ ，表示每個卷積核只需要 $75$ 個參數。
10個不同的卷積核，就需要 $10 ? 75 = 750$ 個卷積核參數。
如果還考慮偏置參數 $b$ ，最終需要 $750 + 10 = 760$ 個參數。

$全連接參數量： 10 ? 28 ? 28 ? (32 ? 32 ? 3 + 1)$

2.10 局部特征提取

? 通過卷積操作，CNN具有局部感知性，能夠捕捉輸入數據的局部特征，這在處理圖像等具有空間結構的數據時非常有用。

2.11 PyTorch卷積層 API

在這里插入圖片描述

test01 函數使用一個多通道卷積核進行特征提取, test02 函數使用 3 個多通道卷積核進行特征提取:

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import osdef showimg(img):plt.imshow(img)# 隱藏刻度plt.axis("off")plt.show()def test001():dir = os.path.dirname(__file__)img = plt.imread(os.path.join(dir, "彩色.png"))# 創建卷積核# in_channels：輸入數據的通道數# out_channels：輸出特征圖數，和filter數一直conv = nn.Conv2d(in_channels=4, out_channels=1, kernel_size=3, stride=1, padding=1)# 注意：卷積層對輸入的數據有形狀要求 [batch, channel, height, width]# 需要進行形狀轉換  H, W, C -> C, H, Wimg = torch.tensor(img, dtype=torch.float).permute(2, 0, 1)print(img.shape)# 接著變形：CHW -> BCHWnewimg = img.unsqueeze(0)print(newimg.shape)# 送入卷積核運算一下newimg = conv(newimg)print(newimg.shape)# 蔣NCHW->HWCnewimg = newimg.squeeze(0).permute(1, 2, 0)showimg(newimg.detach().numpy())# 多卷積核
def test002():dir = os.path.dirname(__file__)img = plt.imread(os.path.join(dir, "彩色.png"))# 定義一個多特征圖輸出的卷積核conv = nn.Conv2d(in_channels=4, out_channels=3, kernel_size=3, stride=1, padding=1)# 圖形要進行變形處理img = torch.tensor(img).permute(2, 0, 1).unsqueeze(0)# 使用卷積核對圖片進行卷積計算outimg = conv(img)print(outimg.shape)# 把圖形形狀轉換回來以方便顯示outimg = outimg.squeeze(0).permute(1, 2, 0)print(outimg.shape)# showimg(outimg)# 顯示這些特征圖for idx in range(outimg.shape[2]):showimg(outimg[:, :, idx].squeeze(-1).detach())if __name__ == "__main__":test002()