在自然語言處理領域，人們經常需要比較字符串，這些字符串可能是單詞、句子、段落甚至是整個文檔。如何快速判斷兩個單詞或句子是否相似，或者相似度是好還是差。這類似于我們使用手機打錯一個詞，但手機會建議正確的詞來修正它，那么這種如何判斷字符串相似度呢？本文將詳細介紹這個問題。

字符串相似度

當我們有兩個數字時，我們可以通過從一個數字中減去另一個數字并觀察結果的符號和大小來輕松比較它們。這種比較方式也可以用于向量，并且有許多方法可以做到這一點。例如常見的：余弦距離、歐幾里得距離、曼哈頓距離、閔可夫斯基公式的p距離等等

但是對于字符串來說就比較復雜了，因為有時需要比較單詞、句子或一般的字符串。一種簡單的方法是比較字符串或單詞之間的公共字母。

總的來說，有三種主要類型的算法用于衡量字符串的相似度，我們將一一介紹：

1. 基于編輯的算法
2. 基于令牌的算法
3. 基于序列的算法

基于編輯的算法

基于編輯的算法，也被稱為基于距離的算法，通過測量將一個字符串轉換成另一個字符串所需的最少單字符操作（插入、刪除或替換）數量來衡量。操作次數越多，相似度（距離）就越低（高）。這一指標為許多其他字符串相似度技術提供了基礎，并廣泛用于拼寫檢查、自動糾錯和DNA序列分析。

注意：這里的每個字符和每個操作都具有相同的重要性

1、Hamming 距離

該度量標準用于測量兩個等長字符串的不相似度，方法是將一個字符串疊加在另一個字符串上，并計算有多少位置的字符不同。漢明要求是長度一致的，但是一些庫可以忽略長度條件，所以算法并不適用于處理長度不相同的2個字符串。

 >> import textdistance as td>> td.hamming('book', 'look')1>> td.hamming.normalized_similarity('book', 'look')0.75>> td.hamming('bellow', 'below')3>> td.hamming.normalized_similarity('Below', 'Bellow')0.5

在第一個示例中，有一個不同的字符。這使得距離等于1，歸一化相似度等于（4-1）/4 = 75%。在第二個示例中，比較“bellow”和“below”，前三個字母相同，但接下來的三個字母不同。因此，距離是3，歸一化相似度是（6-3）/6 = 50%。

2、Levenshtein 距離

Levenshtein 距離是最常用的基于編輯的算法，是一個字符串相似度度量標準，用于測量將一個字符串轉換成另一個字符串所需的最少單字符允許操作（插入、刪除或替換）的數量。它提供了一個量化的度量，表明兩個字符串有多不同。它沒有像Hamming 距離那樣的序列長度條件。

 >> td.levenshtein('book', 'look')1>> td.levenshtein.normalized_similarity('book', 'look')0.75>> td.levenshtein('bellow', 'below')1>> td.levenshtein.normalized_similarity('Below', 'Bellow')0.84

在第一個示例中，可以通過替換一個字母來得到另一個單詞，因此歸一化相似度是（4-1）/4 = 75%。在第二個示例中，有一個插入操作，因此距離是1，歸一化相似度是（6-1）/6 = 84%。

3、Damerau-Levenshtein距離

Damerau-Levenshtein距離是Levenshtein 距離的一個變種，它還包括了置換操作。它測量轉換一個字符串到另一個字符串所需的四種操作的數量。置換涉及交換兩個相鄰字符。

注意：不能置換兩個不相鄰的符號，因此，“stop”和“spot”之間的距離不是1，而是兩次（兩次替換）。

 >> td.levenshtein('act', 'cat')2>> td.levenshtein.normalized_similarity('act', 'cat')0.34>> td.damerau_levenshtein('act', 'cat')1>> td.damerau_levenshtein.normalized_similarity('act', 'cat')0.67

Levenshtein需要替換兩個字母‘a’和‘c’，但由于這兩個字母是相鄰的，我們可以使用Damerau-Levenshtein算法通過一次操作進行置換，這樣就使相似度結果翻倍。這種算法在自然語言處理領域得到了廣泛應用，如拼寫檢查和序列分析。

4、Jaro 相似度

這個算法不是一種距離測量，而是一個介于0和1之間的相似度得分。

Jaro 算法基于匹配字符的數量以及類似Damerau-Levenshtein的置換，但它沒有鄰近性約束。該方法使用了一個直觀的公式：

只有當s1和s2中的兩個字符相同且相距不超過max(|s1|, |s2|)/2 - 1個字符時，才被視為匹配。

如果沒有找到匹配字符，那么這兩個字符串就被認為不相似，賈羅相似度為0。但如果找到了匹配字符，那么我們就計算置換的數量。

 >> td.jaro('bellow', 'below')0.94>> td.jaro('simple', 'plesim')0>> td.jaro('jaro', 'ajro')0.92

在第一個示例中，有5個匹配字符和一個插入（這不是置換操作），因此Jaro 相似度為1/3*(5/6+5/5+6/6)。在第二個示例中，有0個匹配字符，因為共同字符不在max(|s1|, |s2|)/2-1的范圍內。這就是為什么相似度為0的原因。在最后一個示例中，有4個匹配字符和第一和第二字母之間的1個置換操作，因此相似度為1/3 * (4/4+4/4+3/4) = 0.91。

5、Jaro-Winkler相似度

Jaro-Winkler相似度是Jaro相似度的一種修改。它旨在給字符串的公共前綴更多的權重。這將使得前l個字符相同的字符串得到更高的分數。其公式為：

 >> td.jaro("simple", "since")0.7>> t.jaro_winkler("simple", "since")0.76

由于兩個字符串有兩個共同的前綴字母。Jaro-Winkler相似度大于Jaro相似度：0.7 + 0.12(1–0.7) = 0.7 + 0.06 = 0.76。

6、Smith–Waterman相似度

Smith–Waterman算法是一種動態規劃算法，用于尋找兩個序列之間的最優局部對齊。與尋找最優全局對齊的Needleman-Wunsch算法不同，Smith–Waterman算法識別序列內最佳匹配的子序列，這使其比Needleman-Wunsch算法更具相關性。

該算法基于一個評分矩陣為每個可能的局部對齊分配一個分數，該矩陣定義了字符對之間的相似性或不相似性。它尋找序列中得分最大的區域，表示最佳的局部匹配。

Smith–Waterman算法在生物信息學中特別有用，用于識別生物序列中的相似區域或基序，如DNA或蛋白質序列，而不是尋找整個序列的相似性。它允許檢測可能具有生物學意義的局部相似性。

 >> td.smith_waterman("GATTACA", "GCATGCU")3>> td.smith_waterman("GATTACA", "GCATGCU")0.43

基于令牌的算法

基于令牌的算法側重于根據字符串的構成令牌或單詞（但有時令牌只是字符）比較字符串。

1、Jaccard 相似度

Jaccard 距離是衡量兩個集合之間相似度的一種方法。它通過比較集合中的共享元素與它們總的組合元素來量化集合的相似程度。要計算它，你需要找到交集（共享元素）的大小除以并集（所有獨特元素）的大小。

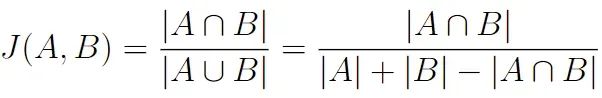
 >> td.jaccard('jaccard similarity'.split(), "similarity jaccard".split())1>> td.jaccard('jaccard similarity'.split(), "similarity jaccard jaccard".split())0.66

我們可以看到，Jaccard 相似度并不考慮字符串單詞的順序。

textdistance包的實現考慮了重復元素，但使用上述公式的經典算法在第二個示例中會給出1的結果。如果你沒有將序列分割成單詞，算法將會將其分割成字符，并對它們應用Jaccard 公式。

如果你了解過目標檢測的算法，你會常聽到過一個單詞 “交并比（Intersection of Union，IoU）”他其實計算的就是Jaccard 相似度。

2、S?rensen-Dice 相似度

S?rensen-Dice 相似度或系數是一種衡量兩個集合之間相似度的指標，類似于Jaccard 相似度。它常用于數據分析、文本挖掘和圖像處理等領域。你最常聽到的一個名字是Dice系數，就是它了。

它的計算方法是找到兩個集合之間共享元素（交集）數量的兩倍與集合大小之和的比例。相似度的公式如下：

 >> td.sorencen('jaccard similarity'.split(), "similarity jaccard".split())1>> td.sorencen('jaccard similarity'.split(), "similarity jaccard jaccard".split())0.8

如果用集合的角度看，把相交作為正類，不相交作為負類，那么我們比較的相似度應該是預測為正類的集合與真實正類集合兩者之間的相似度，換成上述四個值理解，也就是：

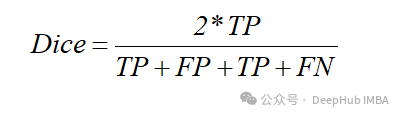
我們再看看f1score的計算公式

F1-score和Dice是相等的，就是這樣。

S?rensen-Dice 相似度與Jaccard 相似度唯一的區別是前者更強調共享元素。

S?rensen-Dice相似度在處理二進制數據或元素的存在與否很重要的情況下特別有用。它提供了一種衡量相似度的方法，考慮了集合的大小并強調了共享元素。

它們之間的關系是：

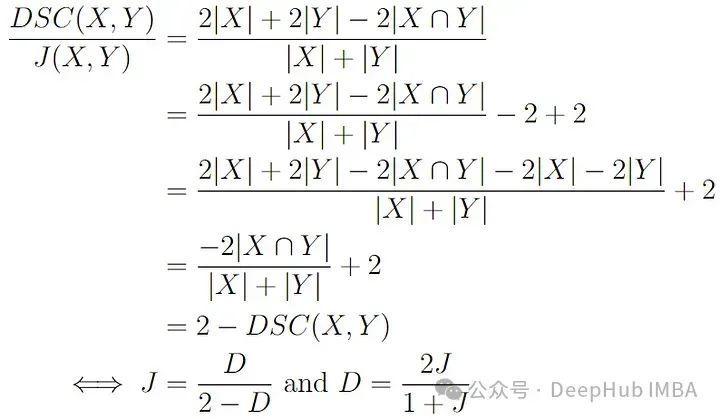
3、Tversky 相似度

Tversky 指數是一種相似度算法，用于量化兩個集合之間重疊的程度，同時考慮到假陽性和假陰性。它在處理不平衡數據或集合中元素的存在或缺失具有不同重要性的情況下特別有用。我們可以選擇強調共有的詞（字符）或非共享的詞。

其定義公式如下：

Tversky基指數可以被視為S?rensen-Dice 和Jaccard 算法的一種泛化。

 >> td.sorencen('tversky similarity'.split(), "similarity tversky tversky".split())0.8>> tversky = td.Tversky(ks=(0.5, 0.5))>> tversky('tversky similarity'.split(), "similarity tversky tversky".split())0.8>> td.jaccard('tversky similarity'.split(), "similarity tversky tversky".split())0.67>> tversky = td.Tversky(ks=(1, 1))>> tversky('tversky similarity'.split(), "similarity tversky tversky".split())0.67>> tversky = td.Tversky(ks=(0.2, 0.8))>> tversky('tversky similarity'.split(), "similarity tversky tversky".split())0.74

Tversky基指數可以平衡集合中不同類型元素的重要性，使其適用于各種應用，如信息檢索、數據挖掘和醫學診斷。

4、重疊相似度

重疊系數又被稱作Szymkiewicz-Simpson系數，是兩個集合之間的一種簡單相似度。它計算的是集合交集大小與較小集合大小的比例。重疊系數在處理二進制數據或元素的存在與否很重要的情況下特別有用。其公式如下：

這個簡單的公式也意味著，如果一個集合是另一個集合的子集。

 >> td.overlap('overlap similarity'.split(), "similarity overlap overlap".split())1.0

5、余弦相似度

余弦相似度是一種廣泛使用的相似度測量方法，用于量化多維空間中兩個非零向量之間角度的余弦值。它通常用于比較文檔、文本或其他高維數據點之間的相似度。余弦相似度捕捉向量的方向或取向，而不是它們的大小。

兩個向量A和B之間的余弦相似度公式如下：

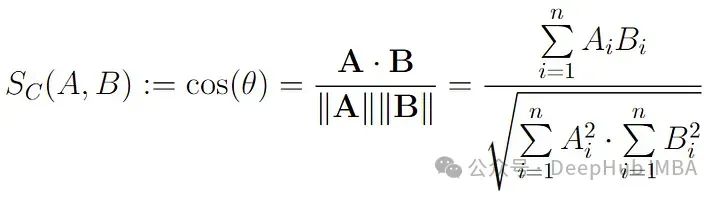
其中A.B表示向量A和B之間的點積，||A||表示向量A的歐幾里得范數。

這種相似度測量結果的范圍從-1（表示完全相反）到1（表示完全相同）。值為0表示正交或去相關，而介于兩者之間的值表示不同程度的相似性或不相似性。

在文本匹配中，屬性向量A和B通常表示文檔的術語頻率向量。余弦相似度作為一種機制，用于在比較時標準化文檔長度。在信息檢索的背景下，兩個文檔之間的余弦相似度范圍在0到1之間，因為術語頻率不能為負。即使使用TF-IDF權重，兩個術語頻率向量之間的角度也不會超過90°。

 >> td.cosine('cosine'.split(), "similarity".split())0>> td.cosine('cosine sim'.split(), "cosine sim sim".split())0.81

textdistance在計算余弦相似度時使用的方法與標準相似度不同。所以建議使用scikit-learn的余弦相似度計算，對于第二個示例，其結果為0.94：

A = [1, 1]；B = [1, 2]，所以A.B = 3，因此cos(θ) = 3/√(2*5) = 0.94。

6、N-gram相似度

N-gram比較算法是一種通過分析兩個字符串中連續n個字符的子序列（稱為n-gram）來衡量它們之間相似度的方法。N-gram本質上是從給定字符串中提取的長度為n的子字符串。這種算法常用于文本分析、自然語言處理和相似度比較任務。N-gram比較算法的過程包括以下步驟：

N-gram提取：將每個輸入字符串分割成重疊的n個字符的序列。

計數N-gram：統計兩個字符串中每個獨特n-gram的出現次數。

計算相似度：比較兩個字符串之間的n-gram計數，并計算相似度分數。相似度分數可以使用各種度量方法計算，常用的選項包括賈卡德相似度和余弦相似度。

讓我們舉一個例子，比較兩個有拼寫錯誤的單詞：（trigrasm 和 trigrams）

 >> trigrams = {"tri", "rig", "igr", "gra", "ram", "ams"}>> trigrasm = {"tri", "rig", "igr", "gra", "ras", "asm"}# there are 8 unique grams in our example so# there are 4 shared words and 4 different ones>> result = 4/80.5

N-gram比較對于各種與文本相關的任務非常有用，例如文檔相似度分析、抄襲檢測和機器翻譯。它捕捉文本中的局部模式，并可以提供關于字符串結構相似性的洞察。選擇n（n-gram的長度）可以影響比較的粒度和敏感性。但是當處理短字符串時，這種算法會失效，其缺點在于該算法對不同的grams給予了更多的重視，而不是共享的grams。

基于序列的算法

基于序列的算法更側重于分析和比較整個序列，而不是像基于令牌的算法那樣比較序列中的令牌。這些算法在處理DNA序列、蛋白質序列或自然語言句子時尤其有價值。這里有一些示例性的例子：

1、Ratcliff-Obershelp相似度

Ratcliff-Obershelp相似度或Gestalt模式匹配是一種字符串相似度測量方法，側重于基于兩個字符串之間的共同子字符串來找到相似性。它特別適用于比較具有相似結構但可能在細微修改、刪除或插入方面有所不同的字符串。該算法根據兩個字符串之間最長公共子字符串的長度分配相似度分數。

Ratcliff-Obershelp算法的工作方式如下：

找到最長公共子字符串（LCS），在兩個輸入字符串之間識別最長的公共子字符串。這是通過找到在兩個字符串中以相同順序出現的公共字符序列來完成的。

然后首先移除LCS部分，并在同一位置進行分割。這將字符串分割成兩部分：一部分在公共部分的左邊，另一部分在右邊。然后取兩個字符串的左部分，再次應用此過程以找到它們的LCS。同樣的過程也適用于右部分。繼續遞歸這個過程，直到任何分割部分小于一定的設定值。

最后使用前面提到的Sorensen-Dice公式計算相似度分數。這個分數是共享字符數的兩倍，除以兩個字符串中的總字符數。

下面通過比較“RO pattern matching”和“RO practice”來清晰地解釋這個算法。

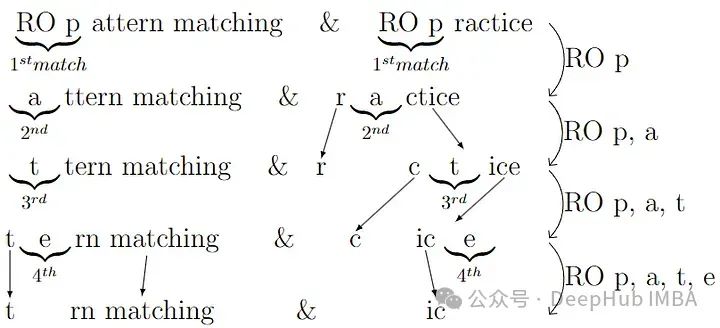
共同的子字符串是“RO p”（4個字符）、‘a’（1個字符）、‘t’（1個字符）、‘e’（1個字符）。這意味著相似度為2*(4+1+1+1)/(19 + 11)=0.467。

但是這個算法有兩個致命的缺點，第一個是它的復雜性，為O(n3)，另一個是該算法不是可交換的，這意味著D(X, Y) != D(Y, X)。

對于第二個問題，我們來驗證一下，第一個例子我們有D(“RO pattern matching”, “RO practice”)。讓我們計算另一種方式：

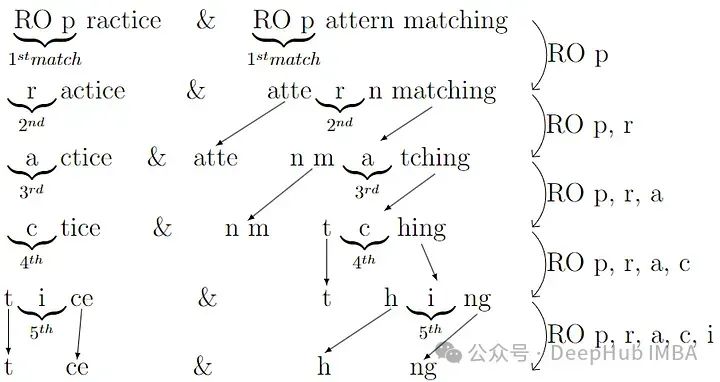
 >> s1, s2 = "RO PATTERN MATCHING", "RO PRACTICE">> td.ratcliff_obershelp(s1, s2), td.ratcliff_obershelp(s2, s1), len(s1), len(s2)(0.46, 0.53, 19, 11)

共同的子字符串是“RO p”（4個字符）、‘r’（1個字符）、‘a’（1個字符）、‘c’（1個字符）、‘i’（1個字符）。這意味著相似度為2*(4+1+1+1+1)/(19 + 11)=0.53。

這個例子展示了Ratcliff-Obershelp算法不可交換性的特點，即從不同的方向比較相同的字符串對可能得到不同的相似度分數。這一性質在需要對稱相似度的應用中可能是一個限制。

2、最長公共子字符串/子序列相似度

最長公共子字符串算法是一種字符串相似度算法，專注于找出兩個字符串之間的最長公共子字符串。它通過識別兩個字符串共享的最長連續字符序列來衡量字符串之間的相似度。相似度得分可以通過將最長公共子字符串的長度除以最長字符串的長度來計算。

與子字符串不同，子序列不要求在原始序列中占據連續位置。因此，最長公共子序列總是大于最長公共子字符串。相似度得分的計算方式與后者相同。

以下示例：

 >> s1, s2 = "RO PATTERN MATCHING", "RO PRACTICE">> td.lcsstr(s1, s2), td.lcsseq(s2, s1), td.lcsseq(s2, s1)('RO P', 'RO PRATC', 'RO PRACI')>> td.lcsstr.normalized_similarity(s1, s2), td.lcsseq.normalized_similarity(s1, s2)(0.21, 0.42)

在上述示例中可以看到最長公共子字符串總是具有連續字符的子字符串，但在最長公共子序列中沒有這個約束。

(A, B)的最長公共子序列與(B, A)不同。實際上可以在上面的例子中看到不同的結果（RO PRATC）和（RO PRACI）。

總結

在本文中，我們深入探討了三個基本算法類別：基于編輯的算法、基于令牌的算法和基于序列的算法。需要記住的重要點是：

基于編輯的算法：

• Damerau-Levenshtein和Jaro winkler距離通過編輯操作量化字符級相似度。
• 適合強調單字符更改和更正的應用。
• 對于拼寫檢查、光學字符識別、字符精確度和文本自動糾正非常有價值。

基于令牌的算法：

• Jaccard 和S?rensen-Dice相似度關注令牌集，忽略序列。
• 對于文檔聚類、抄襲檢測和推薦系統有效。
• 強調存在而非順序，有助于分類。
• 可用于內容分類和文檔比較。

基于序列的算法：

• 最長公共子序列（LCS）和Ratcliff/Obershelp方法保留順序。
• 對于DNA序列對齊、文本近重復檢測和版本控制至關重要。
• 提供字符串內部結構關系的洞察。

沒有單一的方法適用于所有情景，每一類算法都有其優勢，適應特定的需求和背景。所以我們總結了這些算法，一個具備這些多樣化技術知識的優秀數據科學家可以利用它們的綜合力量來解決字符串相似度分析中的廣泛挑戰。

作者：Yassine EL KHAL

https://avoid.overfit.cn/post/43c11a3fee684fecb81eebf5647159aa