筆者近期上了國科大周曉飛老師《強化學習及其應用》課程，計劃整理一個強化學習系列筆記。筆記中所引用的內容部分出自周老師的課程PPT。筆記中如有不到之處，敬請批評指正。

---

總的來說，DP方法就是在已知bellman方程的環境參數（回報R和轉移概率P）的情況下，求取最優策略$u^{?}$和最優值$v^{?}$。

2.1 動態規劃：策略收斂法/策略迭代法

總體思路：算V --> 算Q --> 策略改進 （不斷重復）
初始化最優策略 u，
Step1 策略評估: 確定當前策略 𝜋 的值函數$V^{\pi }$，可通過下面的式子求解。

Step2 計算動作值函數Q: 使用值函數$V^{\pi }$來計算每個狀態-動作對的動作值函數$Q^{\pi }(s,a)$。這一步是為了計算在當前策略 𝜋 下，每個狀態-動作對的期望回報。

Step3 策略改進: 對每個狀態 𝑠 選擇能使$Q^{\pi }(s,a)$最大的動作𝑎，從而形成新的策略 𝜋′。這一步是為了更新策略，使其更接近最優策略。

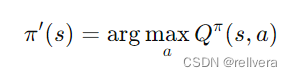
Step4: goto Step1, 直到最優策略ｕ不變。

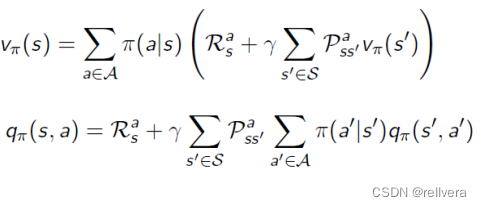
2.2 動態規劃：值迭代法

值迭代（Value Iteration）是一種用于求解馬爾可夫決策過程（MDP）的經典動態規劃算法。它通過迭代地更新值函數，逐步逼近最優值函數$V^{?}$ ，最終得到最優策略${\pi }^{?}$。

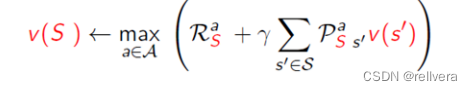
值迭代一般分為這幾個步驟：
step1 初始化：設定初始值函數$V(s)$為零或其他任意值。
step2 迭代更新：對于每個狀態 𝑠 ，根據當前值函數$V_k$計算新的值函數$V_{k+1}$。這個更新過程通過遍歷所有狀態和所有可能的動作，計算在每個狀態下采取每個動作所能獲得的期望累計獎勵，并選擇其中的最大值作為新的值函數值。

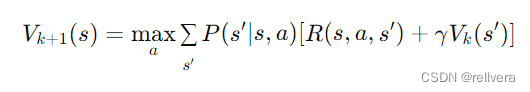
step3 收斂判定：當值函數的變化小于某個預設的閾值 𝜃 時，認為值函數已經收斂，可以停止迭代。

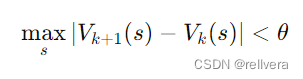
step4 策略提取：在值函數收斂后，通過值函數$V^{?}$ 提取最優策略${\pi }^{?}$：

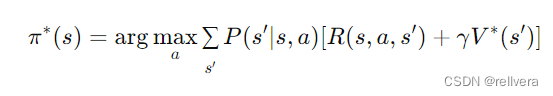
關于值迭代，也有很多處理技巧，這里簡單介紹三種。
（1）In-place Dynamic Programming
在標準的值迭代過程中，我們通常會維護兩個值函數，一個用于保存當前迭代的結果，另一個用于保存上一次迭代的結果。而在 In-place Dynamic Programming 中，我們只使用一個值函數數組，在每次更新時直接覆蓋舊的值。
特點：只需要一個數組來存儲值函數，減少了內存消耗。

（2）Prioritized Sweeping
是一種加速值迭代的方法，通過優先更新那些對值函數變化影響較大的狀態，從而提高收斂速度。

（3）Real-time Dynamic Programming (RTDP)
是一種在實際運行過程中更新值函數的方法，適用于在線學習。