1.引言

1.1.討論的目標

閱讀并理解本文后，大家應能夠：

• 掌握如何為具有離散潛在變量的模型設定參數
• 在可行的情況下，使用精確的對數似然函數來估計參數
• 利用神經變分推斷方法來估計參數

1.2.導入相關軟件包

# 導入PyTorch庫，用于深度學習相關的操作。
import torch
# 導入NumPy庫，用于進行科學計算。
import numpy as np
# 導入Python的random庫，用于設置隨機數生成器的種子。
import random
# 導入matplotlib.pyplot，用于繪圖。
import matplotlib.pyplot as plt
# 導入PyTorch的神經網絡模塊。
import torch.nn as nn
# 導入PyTorch的函數庫，用于一些常用的操作，如激活函數。
import torch.nn.functional as F
# 導入PyTorch的分布庫，用于處理概率分布。
import torch.distributions as td# 從itertools庫導入chain函數，用于迭代多個可迭代對象。
from itertools import chain
# 從collections庫導入defaultdict和OrderedDict，用于創建特殊類型的字典。
from collections import defaultdict, OrderedDict
# 從tqdm.auto導入tqdm，用于顯示進度條。
from tqdm.auto import tqdm# 從IPython.display導入set_matplotlib_formats，用于設置matplotlib的圖形格式。
from IPython.display import set_matplotlib_formats
# 設置matplotlib圖形的格式為SVG和PDF，SVG格式適合網頁顯示，PDF格式適合打印。
set_matplotlib_formats('svg', 'pdf') 
# 導入matplotlib配置，用于設置圖形的全局參數。
import matplotlib
# 設置matplotlib圖形的線寬。
matplotlib.rcParams['lines.linewidth'] = 2.0# 確保matplotlib圖形在Jupyter Notebook中以inline方式顯示。
%matplotlib inline# 定義一個函數seed_all，用于設置所有隨機數生成器的種子，以確保實驗的可復現性。
def seed_all(seed=42):# 設置NumPy的隨機種子。np.random.seed(seed)# 設置Python內置random模塊的種子。random.seed(seed)# 設置PyTorch的隨機種子。torch.manual_seed(seed)# 調用seed_all函數，設置默認的隨機種子。
seed_all()

1.3.數據準備

為了本文的實驗驗證，我們將使用玩具圖像數據集(FashionMNIST)。這些數據集包含固定維度的觀測值，因此設計編碼器和解碼器相對簡單。通過這種方式，我們可以將注意力集中在概率性質的核心部分。

# 從torchvision.datasets導入FashionMNIST數據集。
from torchvision.datasets import FashionMNIST
# 導入torchvision的transforms模塊，用于數據預處理。
from torchvision import transforms
# 導入ToTensor轉換，用于將PIL圖像或Numpy數組轉換為`FloatTensor`。
from torchvision.transforms import ToTensor
# 從torch.utils.data導入random_split和Dataset，用于數據集的劃分和創建。
from torch.utils.data import random_split, Dataset
# 從torch.utils.data.dataloader導入DataLoader，用于創建數據加載器。
from torch.utils.data.dataloader import DataLoader
# 從torchvision.utils導入make_grid，用于將圖像集合排列成一個網格。
from torchvision.utils import make_grid
# 導入PyTorch的優化器模塊。
import torch.optim as opt# 設置數據集的路徑。
DATASET_PATH = "../../data"
# 根據是否有可用的GPU，設置運行設備。
my_device = torch.device("cuda:0") if torch.cuda.is_available() else torch.device("cpu")# 定義一個二值化轉換的Dataset類。
class Binarizer(Dataset):def __init__(self, ds, threshold=0.5):self._ds = ds  # 原始數據集self._threshold = threshold  # 二值化的閾值def __len__(self):# 返回數據集的大小。return len(self._ds)def __getitem__(self, idx):# 根據索引idx獲取數據，并進行二值化處理。x, y = self._ds[idx]return (x >= self._threshold).float(), y# 加載FashionMNIST數據集，并應用數據增強變換。
dataset = FashionMNIST(root=DATASET_PATH, train=True, download=True,transform=transforms.Compose([transforms.Resize(64), transforms.ToTensor()]))
# 打印出第一張圖片的形狀。
img_shape = dataset[0][0].shape
print("Shape of an image:", img_shape)# 設置驗證集的大小。
val_size = 1000
# 計算訓練集的大小。
train_size = len(dataset) - val_size
# 劃分訓練集和驗證集。
train_ds, val_ds = random_split(dataset, [train_size, val_size])# 打印訓練集和驗證集的大小。
print(len(train_ds), len(val_ds))# 設置是否將數據二值化的標志。
bin_data = True
if bin_data:# 如果需要，將訓練集和驗證集轉換為二值化數據集。train_ds = Binarizer(train_ds)val_ds = Binarizer(val_ds)# 設置批大小。
batch_size = 64
# 創建訓練集的數據加載器。
train_loader = DataLoader(train_ds, batch_size, shuffle=True, num_workers=2, pin_memory=True)
# 創建驗證集的數據加載器。
val_loader = DataLoader(val_ds, batch_size, num_workers=2, pin_memory=True)# 遍歷訓練集的迭代器。
for images, y in train_loader:# 打印一批圖像的形狀。print('images.shape:', images.shape)# 創建一個圖形，不顯示坐標軸。plt.figure(figsize=(16,8))plt.axis('off')# 將圖像集合排列成一個網格并顯示。plt.imshow(make_grid(images, nrow=16).permute((1, 2, 0)))plt.show()# 展示一張圖像后退出循環。break

2. 潛在變量模型

在本節中，我們將利用神經網絡來定義一個涉及潛在變量的模型，也就是對一組隨機變量的聯合概率分布進行建模，其中部分變量可以被觀察到，而另一部分則不能。

我們特別關注以下兩種隨機變量：

• 一個離散的潛在代碼 $Z\in \mathcal{Z}$
• 一張圖像 $X\in \mathcal{X}$，它是實數空間 ${\mathbb{R}}^D$ 的一個子集

圖像 $x$ 由 $C$ 個顏色通道、寬度 $W$ 和高度 $H$ 定義，因此 $\mathcal{X}$ 屬于 ${\mathbb{R}}^{C\times W\times H}$。由于我們設定了 $D=C\times W\times H$，$\mathcal{X}$ 是具有有限維度的，但這不是必須的（例如，在其他領域中，$\mathcal{X}$ 可能是無限的，包含任意長度的所有句子）。我們可以將像素強度視為離散或連續變量，前提是我們為每種情況選擇了恰當的概率質量函數或概率密度函數。

我們將探討兩種潛在代碼類型：一種是分類代碼 z ∈ { 1 , … , K } z \in \{1, \ldots, K\} z∈{1,…,K}，另一種是組合代碼 z ∈ { 0 , 1 } K z \in \{0, 1\}^K z∈{0,1}K。在這兩種情況下，$\mathcal{Z}$ 都是可數的，但這不是必須的（例如，$z$ 可以是自然數或任意長度的潛在序列）。

我們通過定義一個聯合概率密度函數來指定 $\mathcal{Z}$ 和 $\mathcal{X}$ 上的聯合分布：

$p_{ZX}(z,x|\theta )=p_Z(z|\theta )\times p_{X|Z}(x|z,\theta )$

這里的 $\theta$ 表示神經網絡的參數，這些網絡參數化了概率質量函數 $p_Z$ 和對于任何給定 $z$ 的條件概率密度函數 $p_{X|Z=z}$。

本文中的先驗分布是固定的，但在其他情況下可能并非如此。我們沒有其他預測變量作為條件，但在某些應用場景中可能會有（例如，在圖像描述任務中，我們可能對給定圖像 $x$ 的標題 $y$ 和潛在代碼 $z$ 的聯合分布感興趣；在圖像生成任務中，我們可能對給定標題 $y$ 的圖像 $x$ 和潛在代碼 $z$ 的聯合分布感興趣）。

2.1 先驗網絡

我們的討論首先從定義和描述一個組件開始，這個組件用于參數化先驗分布$p_Z$。

先驗網絡是一種神經網絡，其主要功能是為一批數據實例提供一個固定的先驗分布的參數化表達。

class PriorNet(nn.Module):  """  先驗網絡：用于參數化先驗分布的神經網絡。  在本實驗中，我們的先驗是固定的，因此該神經網絡的前向傳播  只是返回一個具有給定batch_shape的固定先驗。  """  def __init__(self, outcome_shape: tuple):  """  outcome_shape: 單個結果的形狀。  如果你使用一個整數k，我們將會把它轉換為(k,)的元組形式。  """  super().__init__()  if isinstance(outcome_shape, int):  # 如果outcome_shape是整數，則轉換為元組形式  outcome_shape = (outcome_shape,)  self.outcome_shape = outcome_shape  def forward(self, batch_shape):  """  返回批次對應的先驗分布對象。  Args:  batch_shape (tuple): 批次的形狀。  Returns:  td object: 表示先驗分布的torch.distributions對象（待實現）。  Raises:  NotImplementedError: 因為這個函數需要被實現。  """  raise NotImplementedError("需要實現此函數以返回先驗分布對象！")  # 注意：在實際實現中，您可能需要使用torch.distributions中的某個分布類來創建先驗分布對象。  
# 例如，如果您想要一個正態分布的先驗，您可以使用torch.distributions.Normal。

伯努利分布的乘積先驗

當我們的潛在編碼是一個$K$維的比特向量時，每個比特都可以視為數據點的一個屬性。對于這樣的編碼，我們為每一個坐標使用均勻分布的伯努利先驗：

$$p_Z(z)=\prod _{k=1}^K\text{Bernoulli}(z_k|0.5)$$

這意味著每個比特都有0.5的概率是1，0.5的概率是0。

均勻獨熱類別先驗

若潛在編碼是從一個離散集合 { 1 , … , K } \{1, \ldots, K\} {1,…,K}中選取的一個類別，我們可以為該類別使用均勻的先驗分布：

$$p_Z(z)=\text{Categorical}(z|K^{?1}{1}_K)$$

其中，$1_K$是一個$K$維的全1向量。這個先驗確保每個類別被選中的概率都是相等的，即$1/K$。

在實際應用中，我們可以使用“OneHotCategorical”分布來簡化操作，它會自動將類別分布的樣本轉換為獨熱編碼形式。

class BernoulliPriorNet(PriorNet):"""伯努利先驗網絡，用于D維位向量z：p(z) = ∏ p(z[d] | 0.5)，其中p是伯努利分布。"""def __init__(self, outcome_shape):super().__init__(outcome_shape)  # 調用基類的構造函數# 注冊一個不需要梯度的緩沖區logits，初始化為0self.register_buffer("logits", torch.zeros(self.outcome_shape, requires_grad=False).detach())def forward(self, batch_shape):# 計算分布的形狀shape = batch_shape + self.outcome_shape# 使用td.Independent來獲得多變量抽樣的概率質量函數（pmf）# 如果沒有td.Independent，我們將得到多個pmf而不是一個多變量結果空間的pmf# td.Independent將最右邊的維度解釋為結果形狀的一部分return td.Independent(td.Bernoulli(logits=self.logits.expand(shape)), len(self.outcome_shape))class CategoricalPriorNet(PriorNet):"""分類先驗網絡，用于z是K個類別集合中一個類別的一位有效編碼：p(z) = OneHotCategorical(z | torch.ones(K) / K)"""def __init__(self, outcome_shape):super().__init__(outcome_shape)  # 調用基類的構造函數self.register_buffer("logits", torch.zeros(self.outcome_shape, requires_grad=False).detach())def forward(self, batch_shape):shape = batch_shape + self.outcome_shape# OneHotCategorical是對Categorical的包裝，# 在抽取Categorical樣本后，td.OneHotCategorical使用onehot(sample, support_size)對其進行編碼# 在這里我們不需要td.Independent，因為OneHotCategorical是對多變量抽樣的概率分布# 這與伯努利先驗的乘積不同return td.OneHotCategorical(logits=self.logits.expand(shape))# 測試先驗網絡的函數
def test_priors(batch_size=3):prior_net = BernoulliPriorNet(7)print("\n伯努利先驗")print(f" outcome_shape={prior_net.outcome_shape}")p = prior_net(batch_shape=(batch_size,))print(f" 分布: {p}")z = p.sample()  # 抽取一個樣本print(f" 樣本: {z}")print(f" 形狀: sample={z.shape} log_prob={p.log_prob(z).shape}")prior_net = CategoricalPriorNet(7)print("\n分類先驗")print(f" outcome_shape={prior_net.outcome_shape}")p = prior_net(batch_shape=(batch_size,))print(f" 分布: {p}")z = p.sample()print(f" 樣本: {z}")print(f" 形狀: sample={z.shape} log_prob={p.log_prob(z).shape}")# 調用測試函數
test_priors()

伯努利先驗outcome_shape=(7,)
分布: Independent(Bernoulli(logits: torch.Size([3, 7])), 1)
樣本: tensor([[0., 0., 0., 1., 1., 1., 0.],[1., 0., 1., 0., 1., 0., 0.],[1., 0., 0., 1., 1., 1., 1.]])
形狀: sample=torch.Size([3, 7]) log_prob=torch.Size([3])分類先驗outcome_shape=(7,)
分布: OneHotCategorical()
樣本: tensor([[0., 0., 1., 0., 0., 0., 0.],[1., 0., 0., 0., 0., 0., 0.],[0., 0., 0., 0., 1., 0., 0.]])
形狀: sample=torch.Size([3, 7]) log_prob=torch.Size([3])

2.2 條件概率分布

本節我們將通過神經網絡來參數化條件概率分布（CPDs），具體做法是讓神經網絡學習并輸出某個概率質量函數（PMF）或概率密度函數（PDF）的參數。這一步驟對于構建潛在變量模型中的$p_{X|Z=z}$組件至關重要（并且，在后續的發展中，它也將對變分推斷中的$q_{Z|X=x}$組件有所幫助）。

我們的基本策略是，根據用戶選擇的輸入，通過神經網絡映射到由torch.distributions庫支持的PMF或PDF的參數上。

class CPDNet(nn.Module):  """  CPDNet類：一個用于參數化條件概率分布的神經網絡。  假設L是某個選定的分布，x ~ L 是具有outcome_shape形狀的一個結果。  CPDNet的前向傳播方法將多個輸入映射到L的pmf/pdf的參數上，  并返回一個表示L的pmf/pdf的torch.distributions對象。  """  def __init__(self, outcome_shape):  """  初始化方法。  outcome_shape: 單個結果的形狀。  如果傳入一個整數k，則將其轉換為元組形式(k,)。  """  super().__init__()  # 調用父類nn.Module的初始化方法  if isinstance(outcome_shape, int):  # 如果outcome_shape是整數，則轉換為元組形式  outcome_shape = (outcome_shape,)  self.outcome_shape = outcome_shape  def forward(self, inputs):  """  前向傳播方法。  根據輸入`inputs`預測并返回一個torch.distributions對象。  inputs: 形狀為batch_shape + (num_inputs,)的張量，  其中batch_shape是批次形狀，num_inputs是輸入特征的數量。  返回: 一個torch.distributions對象，表示根據輸入預測的條件概率分布。  注意: 該方法需要被子類重寫以實現具體的條件概率分布參數化邏輯。  """  raise NotImplementedError("請在此處實現具體的前向傳播邏輯")  # 注意：在實際使用中，子類應該實現forward方法以完成具體的條件概率分布參數化。

2.2.1 觀測模型

觀測模型定義了給定隱變量$Z=z$時，觀測變量$X$的分布。

如果像素強度是二值化的，我們可以使用$C\times W\times H$個伯努利分布的乘積來表示這個分布，并通過一個神經網絡來聯合參數化這些分布。具體來說，我們有：

$$p_{X|Z}(x|z,\theta )=\prod _{c=1}^C\prod _{w=1}^W\prod _{h=1}^H\mathrm{Bernoulli}(x_{c,w,h}|f_{c,w,h}(z;\theta ))$$

其中，$f_{c,w,h}(z;\theta )$是神經網絡$\mathbf{f}(z;\theta )$的輸出，表示在給定$z$和參數$\theta$時，位置$(c,w,h)$處像素強度為1的概率。這里，$\mathbf{f}(z;\theta )$是一個神經網絡架構，如全連接網絡或轉置卷積層的堆疊，通常被稱為解碼器。

如果像素強度是$[0,1]$范圍內的實數，我們需要選擇一個合適的概率密度函數（pdf）來參數化分布。在這種情況下，一個合適的選擇是連續伯努利分布，它是一個單參數分布，其支撐集是$[0,1]$，與伯努利分布類似。

接下來，我們將設計這個神經網絡$\mathbf{f}$。

class ReshapeLast(nn.Module):  """  輔助層，用于重塑張量的最右側維度。  可以作為 nn.Sequential 的一部分使用。  """  def __init__(self, shape: tuple):  """  shape: 所需的最右側維度形狀  """  super().__init__()  self._shape = shape  def forward(self, input):  # 將最后一個維度重塑為 self.shape  return input.reshape(input.shape[:-1] + self._shape)  def build_ffnn_decoder(latent_size, num_channels, width=64, height=64, hidden_size=512, p_drop=0.):  """  使用具有2個隱藏層的全連接神經網絡（FFNN）將潛在編碼映射到形狀為 [num_channels, width, height] 的張量。  latent_size: 潛在編碼的大小  num_channels: 輸出中的通道數  width: 圖像寬度  height: 圖像高度  hidden_size: 我們首先將 latent_size 映射到 hidden_size，然后使用前饋神經網絡將其映射到 [num_channels, width, height]  p_drop: 線性層之前的dropout率  """  decoder = nn.Sequential(  # 添加dropout層，以防止過擬合  nn.Dropout(p_drop),  # 第一個線性層，從 latent_size 映射到 hidden_size  nn.Linear(latent_size, hidden_size),  # 激活函數，增加模型非線性  nn.ReLU(),  # 再次添加dropout層  nn.Dropout(p_drop),  # 第二個線性層，保持 hidden_size 不變  nn.Linear(hidden_size, hidden_size),  # 再次使用激活函數  nn.ReLU(),  # 第三個dropout層  nn.Dropout(p_drop),  # 第三個線性層，從 hidden_size 映射到 num_channels * width * height  # 這一步是為了將特征展平，方便后續重塑  nn.Linear(hidden_size, num_channels * width * height),  # 使用 ReshapeLast 層將最后一個維度重塑為 [num_channels, width, height]  ReshapeLast((num_channels, width, height)),  )  return decoder

這樣就建立起了一個簡單的FFNN：

# 定義一個全連接神經網絡解碼器，該解碼器從10維的潛在編碼映射到輸出張量  
# 使用該解碼器來處理一個形狀為(5, 10)的張量，該張量包含5個樣本，每個樣本的潛在編碼是10維的  
# 這里使用了torch.zeros來生成一個所有元素都是0的張量作為示例輸入  # 計算解碼器輸出張量的形狀  
output_shape = build_ffnn_decoder(latent_size=10, num_channels=1)(torch.zeros((5, 10))).shape  # build_ffnn_decoder是一個全連接神經網絡解碼器函數，它接受兩個參數：  
# latent_size=10 表示潛在編碼的維度是10  
# num_channels=1 表示輸出張量的通道數是1  # torch.zeros((5, 10)) 生成一個形狀為(5, 10)的張量，其中所有元素都是0  
# 這個張量表示一個批處理大小為5的數據集，每個數據點的潛在編碼是一個10維的向量  # build_ffnn_decoder函數將上述張量作為輸入，并返回一個輸出張量  
# 輸出張量的形狀取決于解碼器的具體結構和num_channels參數  
# 在這里，我們假設解碼器會將10維的潛在編碼映射到一個具有num_channels個通道的圖像上  
# 但具體的寬度和高度需要由解碼器的設計決定，這里并未明確給出  # output_shape變量將保存解碼器輸出張量的形狀  
# 例如，如果解碼器將10維的潛在編碼映射到一個64x64像素的單通道圖像上，  
# 那么output_shape將會是torch.Size([5, 1, 64, 64])

torch.Size([5, 1, 64, 64])

FFNN解碼器的問題是輸出層的大小可能過大。

為了更好地適應我們的數據類型，一個具有適當歸納偏置的架構是卷積神經網絡（CNN），特別是轉置卷積神經網絡（transposed CNN）。接下來，我們將設計一個這樣的解碼器。

class MySequential(nn.Sequential):"""這是一個 nn.Sequential 的版本，它可以處理結構化批次數據（即，具有多個維度的批次數據），即使其中的某些 nn 層不支持結構化數據。思路是僅將 nn.Sequential 包裝在兩次 reshape 調用周圍，這些調用移除并恢復批次維度。"""def __init__(self, *args, event_dims=1):super().__init__(*args)  # 調用基類的構造函數self._event_dims = event_dims  # 存儲事件維度的數量def forward(self, input):# 記錄批次形狀batch_shape = input.shape[:-self._event_dims]# 記錄事件形狀event_shape = input.shape[-self._event_dims:]# 展平批次形狀并獲取輸出output = super().forward(input.reshape((-1,) + event_shape))# 恢復批次形狀return output.reshape(batch_shape + output.shape[1:])def build_cnn_decoder(latent_size, num_channels, width=64, height=64, hidden_size=1024, p_drop=0.):"""將潛在編碼映射到形狀為 [num_channels, width, height] 的張量。latent_size: 潛在編碼的大小num_channels: 輸出中的通道數width: 必須是 64 （目前是這樣）height: 必須是 64 （目前是這樣）hidden_size: 我們首先從 latent_size 映射到 hidden_size，然后使用轉置的 2D 卷積到 [num_channels, width, height]p_drop: 線性層之前的 dropout 比率"""if width != 64:raise ValueError("The width is hardcoded")  # 如果寬度不是64，拋出異常if height != 64:raise ValueError("The height is hardcoded")  # 如果高度不是64，拋出異常# TODO: 改變架構，使 width 和 height 不是硬編碼decoder = MySequential(        nn.Dropout(p_drop),  # Dropout層nn.Linear(latent_size, hidden_size),  # 線性層，從潛在大小到隱藏大小ReshapeLast((hidden_size, 1, 1)),  # 重塑最后一層的維度nn.ConvTranspose2d(hidden_size, 128, 5, 2),  # 轉置卷積層nn.ReLU(),  # 激活層nn.ConvTranspose2d(128, 64, 5, 2),  # 轉置卷積層nn.ReLU(),  # 激活層nn.ConvTranspose2d(64, 32, 6, 2),  # 轉置卷積層nn.ReLU(),  # 激活層nn.ConvTranspose2d(32, num_channels, 6, 2),  # 轉置卷積層event_dims=1  # 設置事件維度)return decoder

# 注釋：  
# 使用自定義的MySequential（假設已定義）作為容器，我們可以將解碼器設計為接受更復雜的批處理形狀。  
# 在這個例子中，我們創建了一個形狀為[3, 5, 10]的零張量，其中3可能表示外部批處理大小，  
# 5表示對于每個外部樣本，我們都有5個內部樣本（例如，多次從潛在空間抽取的樣本），  
# 10則是每個內部樣本的潛在編碼的維度。  
# build_cnn_decoder函數會基于給定的潛在編碼維度（latent_size=10）和輸出通道數（num_channels=1）  
# 來構建一個卷積神經網絡解碼器。  
# 最后，我們調用該解碼器并傳入零張量來檢查其輸出形狀。  
# 注意：這里假設MySequential可以正確處理多維度的輸入，并且解碼器本身也支持這種輸入形狀。
build_cnn_decoder(latent_size=10, num_channels=1)(torch.zeros((3, 5, 10))).shape

現在我們準備設計一款適用于圖像模型的CPDNet，其核心在于結合一個精心選擇的解碼器和一個恰當的分布模型。

以下代碼定義了兩個類，BinarizedImageModel 和 ContinuousImageModel，它們都繼承自 CPDNet 類（在代碼中沒有給出定義）。這兩個類分別實現了二值圖像模型和連續圖像模型，用于定義給定潛在變量$z$下的條件概率分布$p(X|Z=z)$。

class BinarizedImageModel(CPDNet):    """二值圖像模型類，用于定義給定潛在變量 z 的條件概率分布 X|Z=z。"""def __init__(self, num_channels, width, height, latent_size, decoder_type=build_ffnn_decoder, p_drop=0.):super().__init__((num_channels, width, height))  # 調用基類的構造函數# 初始化解碼器，將潛在變量映射到圖像空間self.decoder = decoder_type(latent_size=latent_size, num_channels=num_channels,width=width,height=height,p_drop=p_drop) def forward(self, z):"""返回條件概率分布 cpd X|Z=z。z: 批次形狀 + (潛在維度,)"""# 批次形狀 + (通道數, 寬度, 高度)h = self.decoder(z)        # 返回一個獨立分布的伯努利分布return td.Independent(td.Bernoulli(logits=h), len(self.outcome_shape))class ContinuousImageModel(CPDNet):    """連續圖像模型類，用于定義給定潛在變量 z 的條件概率分布 X|Z=z。"""# 類的構造函數和 forward 方法與二值圖像模型類似，不同之處在于這里使用的是連續伯努利分布def __init__(self, num_channels, width, height, latent_size, decoder_type=build_ffnn_decoder, p_drop=0.):super().__init__((num_channels, width, height))        self.decoder = decoder_type(latent_size=latent_size, num_channels=num_channels,width=width,height=height,p_drop=p_drop) def forward(self, z):"""返回條件概率分布 cpd X|Z=z。z: 批次形狀 + (潛在維度,)"""h = self.decoder(z)        # 返回一個獨立分布的連續伯努利分布return td.Independent(td.ContinuousBernoulli(logits=h), len(self.outcome_shape))# 以下是使用二值圖像模型的示例代碼# 創建觀測模型實例
obs_model = BinarizedImageModel(num_channels=img_shape[0],width=img_shape[1],height=img_shape[2],latent_size=10,p_drop=0.1,
)
print(obs_model)
# 將一批五個 z 映射到 5 個在 [1,64,64]-維二值張量上的分布
print(obs_model(torch.zeros([5, 10])))# 使用不同的解碼器# 創建使用不同解碼器的觀測模型實例
obs_model = BinarizedImageModel(num_channels=img_shape[0],width=img_shape[1],height=img_shape[2],latent_size=10,     p_drop=0.1, decoder_type=build_cnn_decoder
)
print(obs_model)
# 將一批五個 z 映射到 5 個在 [1,64,64]-維二值張量上的分布
print(obs_model(torch.zeros([5, 10])))

2.3 聯合概率分布

我們現在可以將先驗概率和觀測模型融合，形成聯合概率分布。聯合概率分布能夠支持一些關鍵的操作，例如邊緣概率密度的計算、后驗概率密度的評估，以及從該分布中進行抽樣。進行邊緣和后驗評估所需的計算可能是可行的，也可能不可行，具體情況如下所述。

通過聯合概率密度函數，我們可以使用以下公式計算$x$的邊緣概率密度：

$p_X(x|\theta )={\sum }_{z\in \mathcal{Z}}{p}_{ZX}(z,x|\theta )={\sum }_{z\in \mathcal{Z}}{p}_Z(z|\theta )p_{X|Z}(x|z,\theta )$

如果我們假設$\mathcal{Z}$是可數的，那么可以通過枚舉的方式來計算邊緣概率，所需的時間與$\mathcal{Z}$的大小成線性關系。然而，如果$\mathcal{Z}$是不可數無限集，或者其規模組合上非常大（例如，所有可能的$K$維位向量的空間），那么這種邊緣計算將是不可行的。

如果枚舉是可行的，我們還可以通過以下公式計算給定$x$條件下$z$的后驗概率：

$p_{Z|X}(z|x,\theta )=\frac{p_Z(z|\theta )p_{X|Z}(x|z,\theta )}{p_X(x|\theta )}$

當邊緣計算不可行時，我們可以通過直接應用Jensen不等式來獲得一個簡單的下界估計：

$\log p_X(x|\theta )=\log {\sum }_{z\in \mathcal{Z}}{p}_Z(z|\theta )p_{X|Z}(x|z,\theta )\ge {\sum }_{z\in \mathcal{Z}}{p}_Z(z|\theta )\log p_{X|Z}(x|z,\theta )$

利用蒙特卡洛方法，我們可以通過以下方式近似上述求和：

$\frac{1}{S}{\sum }_{s=1}^S\log p_{X|Z}(x|z_s,\theta )\text{其中?}{z}_s～p_Z$

通過重要性采樣，我們可以得到一個更優的下界估計，但這需要我們訓練一個近似分布，正如我們在變分推斷中所做的那樣。

需要記住的是，給定一個數據集$\mathcal{D}$，對數似然函數 $\mathcal{L}(\theta |\mathcal{D})={\sum }_{x\in \mathcal{D}}\log p_X(x|\theta )$ 需要進行邊緣概率密度的評估。如果精確的邊緣計算不可行，我們就無法評估 $\mathcal{L}(\theta |\mathcal{D})$ 以及它對 $\theta$ 的梯度。如果先驗概率是固定的，我們可以使用上述簡單的下界來估計梯度，但這種直接應用Jensen不等式的方法通常會產生一個寬松的界限。

下面定義了一個名為 JointDistribution 的類，它封裝了先驗網絡和條件概率分布（cpd）網絡來創建一個聯合概率分布。這個類提供了一些方法來處理聯合分布，包括抽樣、計算邊緣概率和后驗概率，以及估計對數邊緣密度的下界。

class JointDistribution(nn.Module):"""一個包裝器，用于將先驗網絡和條件概率分布網絡結合起來形成一個聯合分布。"""def __init__(self, prior_net: PriorNet, cpd_net: CPDNet):"""prior_net: 參數化 p_Z 的對象cpd_net: 參數化 p_{X|Z=z} 的對象"""super().__init__()self.prior_net = prior_netself.cpd_net = cpd_netdef prior(self, shape):return self.prior_net(shape)def obs_model(self, z):return self.cpd_net(z)def sample(self, shape):"""通過 prior_net(shape).sample() 返回 z，并通過 cpd_net(z).sample() 返回 x。"""pz = self.prior_net(shape)z = pz.sample()px_z = self.cpd_net(z)x = px_z.sample()return z, xdef log_prob(self, z, x):"""評估聯合結果的對數概率密度。"""batch_shape = z.shape[:-len(self.prior_net.outcome_shape)]        pz = self.prior_net(batch_shape)        px_z = self.cpd_net(z)return pz.log_prob(z) + px_z.log_prob(x)def log_marginal(self, x, enumerate_fn):"""返回 x 的對數邊緣密度。enumerate_fn: 枚舉先驗支持的功能（這對于邊緣化 p(x) = \int p(z, x) dz 是必要的）如果支持是一個（小的）可數有限集，這是有意義的。在這種情況下，可以使用enumerate=lambda p: p.enumerate_support()例如，Categorical 和 OneHotCategorical 支持此功能。如果支持是離散的（例如，位向量），你仍然可以明確地枚舉它，但你需要編寫自定義代碼，因為 torch.distributions 不會為你提供該功能。如果支持是不可數的、可數無限大的，或者無論如何都很大，你需要近似工具（例如變分推斷、重要性采樣等）。"""batch_shape = x.shape[:-len(self.cpd_net.outcome_shape)]pz = self.prior_net(batch_shape)        log_joint = []z = enumerate_fn(pz)px_z = self.cpd_net(z)log_joint = pz.log_prob(z) + px_z.log_prob(x.unsqueeze(0))return torch.logsumexp(log_joint, 0)def posterior(self, x, enumerate_fn):"""返回后驗分布 Z|X=x。由于代碼是離散的，我們通過 `enumerate_fn` 提供的窮盡枚舉，返回所有可能潛在代碼空間上的離散分布。"""batch_shape = x.shape[:-len(self.cpd_net.outcome_shape)]        pz = self.prior_net(batch_shape)        z = enumerate_fn(pz)px_z = self.cpd_net(z)log_joint = pz.log_prob(z) + px_z.log_prob(x.unsqueeze(0))log_joint = torch.swapaxes(log_joint, 0, -1)return td.Categorical(logits=log_joint)def naive_lowerbound(self, x, num_samples: int):"""返回 x 的對數邊緣密度的 MC 下界：log p(x) >= 1/S \sum_s log p(x|z[s])其中 z[s] ~ p_Z"""batch_shape = x.shape[:-len(self.cpd_net.outcome_shape)]pz = self.prior_net(batch_shape)log_probs = []for z in pz.sample((num_samples,)): px_z = self.cpd_net(z)log_probs.append(px_z.log_prob(x))log_probs = torch.stack(log_probs)return torch.mean(log_probs, 0)# 以下是測試聯合分布的函數
def test_joint_dist(latent_size=10, data_shape=(1, 64, 64), batch_size=2, hidden_size=32):    # 測試二值數據的模型# ...（此處省略了部分代碼，遵循上述類定義的邏輯）# 測試連續數據的模型# ...（此處省略了部分代碼，遵循上述類定義的邏輯）# 調用測試函數
test_joint_dist(10)

3. 學習過程

在訓練過程中，我們采用基于隨機梯度的最大似然估計法來估計模型參數$\theta$。對于可處理的模型，我們首先評估其對數似然函數：

$$\begin{array}{rl}\mathcal{L}(\theta |\mathcal{D})& =\sum _{x\in \mathcal{D}}\log p_X(x|\theta )\end{array}$$

其中，$\mathcal{D}$表示訓練數據集，$p_X(x|\theta )$表示給定參數$\theta$下數據$x$的概率。

接著，我們利用隨機小批量數據來估計對數似然函數關于參數$\theta$的梯度：

$$\begin{array}{rl}{?}_{\theta }\mathcal{L}(\theta |\mathcal{D})& \approx \frac{1}{S}\sum _{s=1}^S{?}_{\theta }\log p_X(x^{(s)}|\theta )\\ & \text{其中，}{x}^{(s)}\text{?是從數據集?}\mathcal{D}\text{?中隨機抽取的樣本}\end{array}$$

通過這種方式，我們可以利用小批量數據來近似計算整個數據集上的梯度，從而加速模型的訓練過程。

3.1 可操作的潛變量模型（LVMs）

一個由$K$個組件組成的混合模型在本質上是一個可操作的潛變量模型（LVM）：

$$\begin{array}{rl}{p}_X(x|\theta )& =\frac{1}{K}\sum _{z=1}^K{p}_{X|Z}(x|z,\theta )\end{array}$$

在這個模型中，$p_{X|Z=z}$ 是基于$z$的獨熱編碼的圖像模型。

# 創建一個聯合分布對象，該對象結合了先驗網絡（prior_net）和條件概率分布網絡（cpd_net）  
print(JointDistribution(  # 先驗網絡：一個分類先驗網絡，假設有10個類別（或稱為潛在變量/隱變量）  prior_net=CategoricalPriorNet(10),  # 條件概率分布網絡（CPDNet）：用于從給定的潛在變量生成圖像  cpd_net=BinarizedImageModel(  # 圖像通道數，例如RGB圖像為3，灰度圖像為1  num_channels=img_shape[0],  # 圖像的寬度  width=img_shape[1],  # 圖像的高度  height=img_shape[2],  # 潛在變量的維度大小，與先驗網絡中的類別數相對應  latent_size=10,  # 使用的解碼器類型，這里使用build_ffnn_decoder函數來構建解碼器  # 假設build_ffnn_decoder是一個函數，它返回一個全連接神經網絡（FFNN）解碼器  decoder_type=build_ffnn_decoder  )  
))

3.2 訓練流程

以下是用于通過精確的對數似然函數來評估和訓練潛變量模型（LVM）的詳細訓練流程及其輔助代碼。

def assess_exact(model: JointDistribution, enumerate_fn, dl, device):"""用于估計模型對數似然的包裝器。數據樣本是數據加載器中的所有數據點。model: 可以對 Z 進行精確邊緣化的聯合分布enumerate_fn: 用于枚舉一批數據的 Z 支持的算法將用于評估 `model.log_prob(batch, enumerate_fn)`dl: torch 數據加載器device: torch 設備"""L = 0data_size = 0with torch.no_grad():  # 禁用梯度計算for batch_x, batch_y in dl:  # 遍歷數據加載器中的批次# 計算并累加對數邊緣概率L = L + model.log_marginal(batch_x.to(device), enumerate_fn).sum(0)data_size += batch_x.shape[0]  # 更新數據點數量L = L / data_size  # 計算平均對數似然return L# ...def train_exact(model: JointDistribution, enumerate_fn, optimiser, training_data, dev_data,batch_size=64, num_epochs=10, check_every=10,    grad_clip=5.,report_metrics=['L'],num_workers=2,device=torch.device('cuda:0')):"""model: 可以對 Z 進行精確邊緣化的聯合分布enumerate_fn: 用于枚舉 Z 支持的功能（與 model.log_prob 結合使用）optimiser: pytorch 優化器training_data: 訓練用的 torchvision 數據集dev_data: 驗證用的 torchvision 數據集batch_size: 根據你的內存量可以設置更大num_epochs: 更多的迭代次數可以提高收斂性check_every: 設定檢查開發集性能的頻率device: 運行實驗的設備返回一個日志，記錄了訓練期間計算的數量（用于繪圖）"""# 創建訓練和驗證的數據加載器batcher = DataLoader(training_data, batch_size, shuffle=True, num_workers=num_workers, pin_memory=True)dev_batcher = DataLoader(dev_data, batch_size, num_workers=num_workers, pin_memory=True)total_steps = num_epochs * len(batcher)  # 總步數log = defaultdict(list)  # 記錄訓練和驗證的日志step = 0model.eval()  # 評估模式# 在設備上評估開發集的對數似然log['dev.L'].append((step, assess_exact(model, enumerate_fn, dev_batcher, device=device).item()))# 使用 tqdm 進度條進行訓練with tqdm(range(total_steps)) as bar:for epoch in range(num_epochs):for batch_x, batch_y in batcher:model.train()  # 訓練模式optimiser.zero_grad()  # 清零梯度# 計算損失并反向傳播loss = - model.log_marginal(batch_x.to(device), enumerate_fn).mean(0)log['loss'].append((step, loss.item()))loss.backward()# 梯度裁剪nn.utils.clip_grad_norm_(model.parameters(), grad_clip)optimiser.step()# 更新進度條bar_dict = OrderedDict()bar_dict['loss'] = f"{loss.item():.2f}"bar_dict[f"dev.L"] = "{:.2f}".format(log[f"dev.L"][-1][1])bar.set_postfix(bar_dict)bar.update()# 定期在開發集上評估性能if step % check_every == 0:model.eval()log['dev.L'].append((step, assess_exact(model, enumerate_fn, dev_batcher, device=device).item()))step += 1model.eval()  # 評估模式# 記錄最終的對數似然log['dev.L'].append((step, assess_exact(model, enumerate_fn, dev_batcher, device=device).item()))return log

以下是用于檢查從混合模型中抽取樣本的輔助函數或代碼片段。

def inspect_mixture_model(model: JointDistribution, support_size):  # 從先驗分布中抽取一些樣本進行展示  # _, x_ = model.sample((support_size, 5))  # 這行代碼原樣保留，但可能需要根據實際函數進行調整  # 假設這里從模型中抽取的樣本是圖像，并且我們將其重塑為合適的形狀  # x_ = x_.cpu().reshape(-1, 1, 64, 64)  # 將數據移至CPU并重新整形為圖像格式  # 創建一個繪圖窗口并設置其大小  plt.figure(figsize=(12,6))  # 關閉坐標軸顯示  plt.axis('off')  # 使用make_grid函數將多個圖像合并為一個網格，并重新排列其維度以便可視化  # 注意：make_grid函數通常來自torchvision.utils  plt.imshow(make_grid(x_, nrow=support_size).permute((1, 2, 0)))  # 設置圖的標題為“先驗樣本”  plt.title("先驗樣本")  # 顯示圖像  plt.show()  # 接下來，從每個組件中抽取樣本進行展示  # support_size 是抽取的樣本數量，latent_dim 是潛在空間的維度（但在此代碼中未直接使用）  # support = model.prior(tuple()).enumerate_support()  # 這行代碼假設可以枚舉先驗分布的支持集  # 假設我們從每個組件中抽取了5個樣本，并將它們重塑為圖像格式  # 注意：這里假設obs_model是一個可以從給定潛在變量生成圖像的方法  # x_ = model.obs_model(support).sample((5,)).cpu().reshape(-1, 1, 64, 64)  # 創建一個新的繪圖窗口并設置其大小  plt.figure(figsize=(12,6))  # 再次關閉坐標軸顯示  plt.axis('off')  # 使用make_grid函數將多個圖像合并為一個網格，并重新排列其維度以便可視化  plt.imshow(make_grid(x_, nrow=support_size).permute((1, 2, 0)))  # 設置圖的標題為“組件樣本”  plt.title("組件樣本")  # 顯示圖像  plt.show()

3.2.1.實驗驗證

# 確保實驗的可復現性，通過設置隨機種子。
seed_all()# 創建一個聯合分布模型，該模型由先驗網絡和條件概率分布網絡組成。
mixture_model = JointDistribution(# 先驗網絡，這里使用的是CategoricalPriorNet，它生成類別分布，參數為潛在類別的數量。prior_net=CategoricalPriorNet(10),# 條件概率分布網絡，這里使用的是BinarizedImageModel，它處理圖像數據。# 這個網絡可能是二值化的（binary），也可能是連續的（continuous），具體取決于數據預處理。cpd_net=BinarizedImageModel(num_channels=img_shape[0],  # 圖像的通道數。width=img_shape[1],  # 圖像的寬度。height=img_shape[2],  # 圖像的高度。latent_size=10,  # 潛在變量的維度。# 解碼器的構建函數，這里使用的是全連接神經網絡（feed-forward neural network）。decoder_type=build_ffnn_decoder,# 網絡中的dropout比例。p_drop=0.1,)
).to(my_device)  # 將模型移動到指定的設備上，例如GPU。# 打印模型的摘要信息。
print(mixture_model)# 創建模型的優化器，這里使用的是Adam優化器。
# 優化器會遍歷模型的所有參數，并使用給定的學習率和權重衰減系數進行優化。
mm_optim = opt.Adam(mixture_model.parameters(), lr=1e-3, weight_decay=1e-6)

# 調用train_exact函數來訓練混合模型。
# model參數是之前初始化的混合模型。
# optimiser參數是模型的優化器。
# enumerate_fn是一個函數，用于枚舉模型的支持點。
# training_data是訓練數據集。
# dev_data是開發/驗證數據集。
# batch_size是每個訓練批次的樣本數量。
# num_epochs是訓練周期數，更多的周期有助于模型更好地學習數據。
# check_every是檢查頻率，即每隔多少步在開發集上評估一次模型。
# grad_clip是梯度裁剪的閾值，用于防止梯度爆炸。
# device是模型運行的設備，例如GPU。
log = train_exact(model=mixture_model,optimiser=mm_optim,enumerate_fn=lambda p: p.enumerate_support(),training_data=train_ds,dev_data=val_ds,batch_size=256,num_epochs=1,  # 用更多的周期可以得到更好的模型性能check_every=10,grad_clip=5.,device=my_device
)# 創建一個圖形和兩個子圖，用于繪制訓練損失和開發集上的對數似然。
# sharex=True表示兩個子圖共享x軸，sharey=False表示不共享y軸。
# figsize設置圖形的大小。
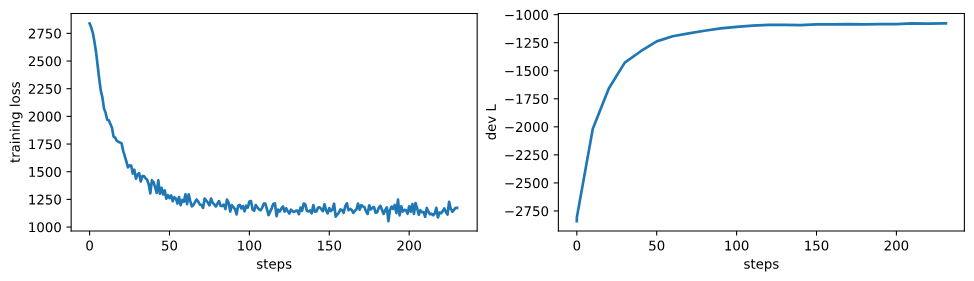
fig, axs = plt.subplots(1, 2, sharex=True, sharey=False, figsize=(12, 3))# 繪制訓練損失。取日志中'loss'鍵對應的數據，繪制其第一列（步驟）和第二列（損失值）。
_ = axs[0].plot(np.array(log['loss'])[:, 0], np.array(log['loss'])[:, 1])
# 設置第一個子圖的y軸標簽為"training loss"。
_ = axs[0].set_ylabel("training loss")
# 設置第一個子圖的x軸標簽為"steps"。
_ = axs[0].set_xlabel("steps")# 繪制開發集上的對數似然。取日志中'dev.L'鍵對應的數據，繪制其第一列（步驟）和第二列（對數似然值）。
_ = axs[1].plot(np.array(log['dev.L'])[:, 0], np.array(log['dev.L'])[:, 1])
# 設置第二個子圖的y軸標簽為"dev L"。
_ = axs[1].set_ylabel("dev L")
# 設置第二個子圖的x軸標簽為"steps"。
_ = axs[1].set_xlabel("steps")

inspect_mixture_model(mixture_model, 10)

混合模型在表達觀測模型的能力上相當有限，它最多只能將數據空間分割成$K$個不同的群組。

然而，因子模型則賦予了觀測模型高達$2^K$種不同的編碼可能性。接下來，我們將構建一個因子模型來克服這一限制。

3.3 難以求解的潛在變量模型（LVMs）

在某些情況下，對潛在變量進行邊緣化處理變得非常復雜（例如，當潛在空間 $\mathcal{Z}$ 是一個 $K$ 維度的二進制向量空間，且 $K$ 的值適中）或者實際上不可行（例如，當 $\mathcal{Z}$ 是一個從 1 到 $K$ 的整數集合，且 $K$ 很大，如 $K>10$）。這時，我們會采用變分推斷的方法，引入一個參數化的近似后驗分布 $q_{Z|X=x}$ 來估計模型的真實后驗分布 $p_{Z|X=x}$，并通過最大化證據下界（ELBO）來估計這個近似和聯合分布。對于單個觀測值 $x$，ELBO 公式如下：

$\mathcal{E}(\lambda ,\theta |\mathcal{D})={\mathbb{E}}_{x～\mathcal{D}}\left[\mathbb{E}\left[\log \frac{p_{ZX}(z,x|\theta )}{q_{Z|X}(z|x,\lambda )}\right]\right]$

$=\left({\mathbb{E}}_{x～\mathcal{D}}\left[\mathbb{E}[\log p_{ZX}(x|z,\theta )]\right]\right)?\left({\mathbb{E}}_{x～\mathcal{D}}\left[\mathrm{KL}(q_{Z|X=x}||p_Z)\right]\right)$

這里，內部期望是針對 $q_{Z|X}(z|x,\lambda )$ 來計算的。

當我們根據數據分布來計算期望時，ELBO 的兩個部分，即期望的對數似然 $\mathbb{E}[\log p_{ZX}(x|z,\theta )]$ 和 Kullback-Leibler 散度項 $\mathrm{KL}(q_{Z|X=x}||p_Z)$，與信息論中的兩個量——失真和速率有關。

我們選擇的近似分布應滿足以下條件：其支持集應包含在先驗分布的支持集中，它應足夠簡單以便于進行抽樣，并且足夠簡單以便于計算樣本的質量。如果可能的話，我們還希望它使得其他量（如熵、相對熵）也是容易計算的。

對于多變量 $z$，我們通常選擇一個分解式的概率分布族。例如，如果 $z$ 是一個 $D$ 維的位向量，則可能選擇如下形式的分布：

$q_{Z|X}(z|x,\lambda )={\prod }_{k=1}^K\mathrm{Bernoulli}(z_k|g_k(x;\lambda ))$

其中 $\mathbf{g}(x;\lambda )$ 位于區間 (0,1) 的 $K$ 維空間內。這種假設被稱為均場近似。

對于分類變量 $z$，原則上邊緣化是可行的（它需要的時間與可能的分類數 $K$ 成線性關系），但對于一些解碼器來說，即使 $K$ 次前向計算也可能太多，因此我們使用一個獨立參數化的分類分布：
$q_{Z|X}(z|x,\lambda )=\mathrm{Categorical}(z|\mathbf{g}(x;\lambda ))$

其中 $\mathbf{g}(x;\lambda )$ 位于 $K?1$ 維的簡單形空間 ${\Delta }_{K?1}$ 內。

3.4 推斷模型

為了構建推斷模型，我們設計了一個條件概率分布網絡（CPD nets），該網絡用于模擬潛變量的條件分布。

在進行下一步之前，我們首先需要設計一個“編碼器”，其功能是將圖像$x\in \mathcal{X}$映射到一個固定大小的向量上，這個向量可以作為圖像$x$的緊湊表示。接下來，我們將開發兩種編碼器：一種基于全連接神經網絡（FFNNs），另一種基于卷積神經網絡（CNNs）。

class FlattenImage(nn.Module):def forward(self, input):# 將輸入數據展平為 (batch_size, -1) 的形狀return input.reshape(input.shape[:-3] + (-1,))def build_ffnn_encoder(num_channels, width=64, height=64, output_size=1024, p_drop=0.):# 使用全連接層構建編碼器encoder = nn.Sequential(FlattenImage(),  # 展平圖像nn.Dropout(p_drop),  # dropout層nn.Linear(num_channels * width * height, output_size//2),  # 線性層nn.ReLU(),  # ReLU激活函數nn.Dropout(p_drop),  # dropout層nn.Linear(output_size//2, output_size//2),  # 線性層nn.ReLU(),  # ReLU激活函數nn.Dropout(p_drop),  # dropout層nn.Linear(output_size//2, output_size),  # 線性層)return encoderdef build_cnn_encoder(num_channels, width=64, height=64, output_size=1024, p_drop=0.):# 檢查是否修改了硬編碼的參數if width != 64 or height != 64 or output_size != 1024:raise ValueError("The width, height, and output_size are hardcoded")# 使用卷積層構建編碼器encoder = MySequential(nn.Conv2d(num_channels, 32, 4, 2),  # 卷積層nn.LeakyReLU(0.2),  # 泄漏ReLU激活函數nn.Conv2d(32, 64, 4, 2),  # 卷積層nn.LeakyReLU(0.2),  # 泄漏ReLU激活函數nn.Conv2d(64, 128, 4, 2),  # 卷積層nn.LeakyReLU(0.2),  # 泄漏ReLU激活函數nn.Conv2d(128, 256, 4, 2),  # 卷積層nn.LeakyReLU(0.2),  # 泄漏ReLU激活函數FlattenImage(),  # 展平圖像event_dims=3  # 設置事件維度)return encoder# 以下是使用構建的編碼器的示例代碼# 使用全連接神經網絡編碼器處理一批五個 [1, 64, 64] 維的圖像
# 將它們編碼為五個 1024 維的向量
build_ffnn_encoder(num_channels=1)(torch.zeros((5, 1, 64, 64))).shape# 結構化批次數據示例 (這里嘗試使用 (3,5) 批次形狀)
build_ffnn_encoder(num_channels=1)(torch.zeros((3, 5, 1, 64, 64))).shape# 使用卷積神經網絡編碼器處理一批五個 [1, 64, 64] 維的圖像
# 將它們編碼為五個 1024 維的向量
build_cnn_encoder(num_channels=1)(torch.zeros((5, 1, 64, 64))).shape# 由于使用了 MySequential，我們也可以處理結構化批次數據
# (這里嘗試使用 (3,5) 批次形狀)
build_cnn_encoder(num_channels=1)(torch.zeros((3, 5, 1, 64, 64))).shape

接下來，我們可以設計一些條件概率分布網絡（CPD nets），這些網絡能夠將圖像的編碼映射到關于$\mathcal{Z}$的概率質量函數（pmf）。

伯努利乘積模型

這種模型適用于參數化固定維度二進制向量的條件概率分布。

獨熱分類模型

這種模型則用于參數化來自有限集合的類別的獨熱編碼的條件概率分布。

代碼定義了幾個類，包括 BernoulliCPDNet 和 CategoricalCPDNet，它們都繼承自 CPDNet 類（在代碼中沒有給出定義）。這些類實現了條件概率分布網絡，用于建模給定輸入下潛在變量的分布。此外，還有一個 test_cpds 函數用于測試這些網絡，以及一個 InferenceModel 類，用于結合編碼器和條件概率分布網絡進行推斷。

class BernoulliCPDNet(CPDNet):"""輸出分布是伯努利分布的乘積。"""def __init__(self, outcome_shape, num_inputs: int, hidden_size: int=None, p_drop: float=0.):"""outcome_shape: 結果的形狀（整數或元組）如果是整數，我們將其轉換為單例元組num_inputs: forward 輸入的最右邊的維度hidden_size: CPDNet 的隱藏層大小（如果跳過則使用 None）p_drop: 在每個 Linear 層之前的 dropout 配置"""# ...（類的其余代碼）def forward(self, inputs):        # 計算并返回伯努利分布的獨立性h = self.encoder(inputs)return td.Independent(td.Bernoulli(logits=self.logits(h)), len(self.outcome_shape))class CategoricalCPDNet(CPDNet):"""輸出分布是分類分布的乘積。"""# 類的構造函數與 BernoulliCPDNet 類似，不同之處在于輸出分布def forward(self, inputs):        # 計算并返回分類分布h = self.encoder(inputs)return td.OneHotCategorical(logits=self.logits(h))# 以下是測試條件概率分布網絡的函數def test_cpds(outcome_shape, batch_size=3, input_dim=5, hidden_size=2):# 測試伯努利條件概率分布網絡cpd_net = BernoulliCPDNet(outcome_shape, num_inputs=input_dim, hidden_size=hidden_size) # ...（函數的其余代碼）# 測試不同的網絡配置
test_cpds(12)
test_cpds(12, hidden_size=None)
test_cpds((4, 5))# 以下是結合編碼器和條件概率分布網絡的推斷模型類class InferenceModel(CPDNet):def __init__(self, cpd_net_type, latent_size, num_channels=1, width=64, height=64, hidden_size=1024, p_drop=0., encoder_type=build_ffnn_encoder):        super().__init__(latent_size)self.latent_size = latent_size    # 將圖像編碼為 hidden_size 維的向量self.encoder = encoder_type(num_channels=num_channels,width=width, height=height,output_size=hidden_size,p_drop=p_drop)# 從 hidden_size 維的編碼映射到 Z|X=x 的 cpdself.cpd_net = cpd_net_type(latent_size, num_inputs=hidden_size, hidden_size=2*latent_size,p_drop=p_drop)def forward(self, x):# 執行推斷模型的前向傳播h = self.encoder(x)        return self.cpd_net(h)

最后但同樣關鍵的是，我們可以將編碼器與我們選擇的條件概率分布網絡（CPD net）相結合。

3.5 神經變分推斷

在訓練我們的生成模型時，我們將采用變分推斷方法，這需要同時訓練一個推斷模型。為了實現這一目標，我們將使用ELBO（證據下界）作為目標函數，并基于得分函數估計法來計算梯度。

盡管傳統的變分自編碼器（VAE）采用了不同的生成模型和梯度估計器，但在現代文獻中，我們常常將這種結合了神經網絡和變分推斷的模型統稱為變分自編碼器。

對于給定的數據點$x$，我們將通過蒙特卡洛估計法來計算ELBO關于$\lambda$的梯度，其表達式如下：

$${?}_{\lambda }\mathcal{E}(\lambda ,\theta |x)=\mathbb{E}\left[r(z,x;\theta ,\lambda ){?}_{\lambda }\log \frac{p_{ZX}(z,x|\theta )}{q_{Z|X}(z|x,\lambda )}\right]$$

其中，“獎勵”函數$r$定義為：

$$r(z,x;\theta ,\lambda )=\log p_{X|Z}(x|z,\theta )$$

然而，由于這個梯度估計器可能會產生較大的噪聲，因此通常通過引入控制變量來改進獎勵函數的估計。控制變量通常是關于$x$、$\theta$和$\lambda$的函數，但不依賴于我們評估獎勵函數的動作$z$。我們將實現這些控制變量作為獎勵函數的包裝器。接下來，我們將確定控制變量的API設計。

class VarianceReduction(nn.Module):"""我們將使用簡單的控制變量形式來減少方差。這些是對獎勵的變換，它們獨立于采樣的潛在變量，但理論上可以依賴于x，以及生成模型和推斷模型的參數。其中一些是可訓練的組件，因此它們也對損失有所貢獻。"""def __init__(self):super().__init__()def forward(self, r, x, q, r_fn):"""返回變換后的獎勵和對損失的貢獻。r: 一批獎勵x: 一批觀測數據q: 策略r_fn: 獎勵函數"""return r, torch.zeros_like(r)# ...class NVIL(nn.Module):"""一個生成模型 p(z)p(x|z) 和一個對該模型真實后驗 p(z|x) 的近似 q(z|x)。近似是為了最大化ELBO 而估計的，聯合分布也是如此。"""def __init__(self, gen_model: JointDistribution, inf_model: InferenceModel, cv_model: VarianceReduction):"""gen_model: 生成模型 p(z)p(x|z)inf_model: 近似后驗 q(z|x)，用于近似 p(z|x)cv_model: 獎勵的可選變換"""super().__init__()self.gen_model = gen_model        self.inf_model = inf_modelself.cv_model = cv_model# 以下是模型參數的獲取方法def gen_params(self):return self.gen_model.parameters()def inf_params(self):return self.inf_model.parameters()def cv_params(self):return self.cv_model.parameters()# 以下是采樣和條件采樣的方法def sample(self, batch_size, sample_size=None, oversample=False):# 從聯合分布中采樣# ...pz = self.gen_model.prior((batch_size,))samples = [None] * (sample_size or 1)        px_z = self.gen_model.obs_model(pz.sample()) if oversample else Nonefor k in range(sample_size or 1):if not oversample:px_z = self.gen_model.obs_model(pz.sample())samples[k] = px_z.sample()x = torch.stack(samples) return x if sample_size else x.squeeze(0)def cond_sample(self, x, sample_size=None, oversample=False):# 給定 x 條件下的采樣# ...qz = self.inf_model(x)samples = [None] * (sample_size or 1)        px_z = self.gen_model.obs_model(qz.sample()) if oversample else None        for k in range(sample_size or 1):if not oversample:px_z = self.gen_model.obs_model(qz.sample())samples[k] = px_z.sample()        x = torch.stack(samples) return x if sample_size else x.squeeze(0)# 以下是計算聯合概率密度的方法def log_prob(self, z, x):# 在生成模型下的聯合結果的對數概率密度# ...return self.gen_model.log_prob(z=z, x=x)# 以下是NVIL模型中使用的方法def DRL(self, x, sample_size=None):"""基于單個數據點但多個潛在樣本的模型的* 失真 D* 速率 R* 對數似然 L的蒙特卡洛估計。"""sample_size = sample_size or 1obs_dims = len(self.gen_model.cpd_net.outcome_shape)batch_shape = x.shape[:-obs_dims]with torch.no_grad():        qz = self.inf_model(x)pz = self.gen_model.prior(batch_shape)R = td.kl_divergence(qz, pz)D = 0ratios = [None] * sample_sizefor k in range(sample_size):z = qz.sample()px_z = self.gen_model.obs_model(z)ratios[k] = pz.log_prob(z) + px_z.log_prob(x) - qz.log_prob(z)D = D - px_z.log_prob(x)ratios = torch.stack(ratios, dim=-1)L = torch.logsumexp(ratios, dim=-1) - np.log(sample_size)            D = D / sample_sizereturn D, R, L# ...def elbo(self, x, sample_size=None):"""ELBO 的蒙特卡洛估計 = -D -R"""# ...D, R, _ = self.DRL(x, sample_size=sample_size)return -D -Rdef log_prob_estimate(self, x, sample_size=None):"""重要性采樣估計的對數 p(x)"""_, _, L = self.DRL(x, sample_size=sample_size)return Ldef forward(self, x, sample_size=None, rate_weight=1.):"""蒙特卡洛估計 - grad ELBO 的替代品x: [batch_size] + data_shapesample_size: 如果是1或更多，我們使用多個樣本sample_size 控制順序計算（for循環）cv: 用于減少方差的可選模塊"""sample_size = sample_size or 1obs_dims = len(self.gen_model.cpd_net.outcome_shape)batch_shape = x.shape[:-obs_dims]qz = self.inf_model(x)pz = self.gen_model.prior(batch_shape)D = 0sfe = 0reward = 0cv_reward = 0raw_r = 0cv_loss = 0for _ in range(sample_size):            z = qz.sample()                px_z = self.gen_model.obs_model(z)raw_r = px_z.log_prob(x) + pz.log_prob(z) - qz.log_prob(z)                r, l = self.cv_model(raw_r.detach(), x=x, q=qz, r_fn=lambda a: self.gen_model(a).log_prob(x))cv_loss = cv_loss + lsfe = sfe + r.detach() * qz.log_prob(z) D = D - px_z.log_prob(x)D = (D / sample_size)sfe = (sfe / sample_size)R = td.kl_divergence(qz, pz)cv_loss = cv_loss / sample_sizeelbo_grad_surrogate = (-D + sfe)        loss = -elbo_grad_surrogate + cv_lossreturn {'loss': loss.mean(0), 'ELBO': (-D -R).mean(0).item(), 'D': D.mean(0).item(), 'R': R.mean(0).item(), 'cv_loss': cv_loss.mean(0).item()}

以下是一個示例

nvil = NVIL(JointDistribution(BernoulliPriorNet(10),BinarizedImageModel(num_channels=img_shape[0],width=img_shape[1],height=img_shape[2],latent_size=10,     p_drop=0.1,decoder_type=build_ffnn_decoder)),InferenceModel(cpd_net_type=BernoulliCPDNet,latent_size=10, num_channels=img_shape[0], width=img_shape[1], height=img_shape[2],        encoder_type=build_ffnn_encoder),VarianceReduction()
)
nvil
for x, y in train_loader:print('x.shape:', x.shape)print(nvil(x))break

3.5.1 訓練算法

由于存在多達三個組件（其中某些控制變量可能具有其自己的參數），因此我們需要同時操作多達三個優化器。

class OptCollection:# 初始化OptCollection類的一個實例。# gen: 表示生成器(generator)的優化器。# inf: 表示判別器(inferior)的優化器。# cv: 可選參數，表示其他組件的優化器，如果存在的話。def __init__(self, gen, inf, cv=None):self.gen = gen  # 存儲生成器的優化器self.inf = inf  # 存儲判別器的優化器self.cv = cv    # 存儲其他組件的優化器，如果沒有則為None# 零化所有優化器的梯度。# 這通常在開始反向傳播之前調用。def zero_grad(self):self.gen.zero_grad()  # 零化生成器優化器的梯度self.inf.zero_grad()  # 零化判別器優化器的梯度if self.cv:            # 如果存在其他組件的優化器self.cv.zero_grad()  # 零化其他組件優化器的梯度# 更新所有優化器的參數。# 這通常在完成反向傳播后調用。def step(self):self.gen.step()  # 更新生成器優化器的參數self.inf.step()  # 更新判別器優化器的參數if self.cv:       # 如果存在其他組件的優化器self.cv.step()  # 更新其他組件優化器的參數

以下是用于評估和訓練模型的輔助代碼段。

from collections import defaultdict, OrderedDict
from tqdm.auto import tqdm# 評估模型的函數，用于估計模型的ELBO、失真度（Distortion）、速率（Rate）和對數似然（Log-likelihood）。
def assess(model, sample_size, dl, device):"""使用數據加載器中的所有數據點來估計模型的ELBO、失真度、速率和對數似然的包裝器。"""# 初始化變量D = 0  # 失真度R = 0  # 速率L = 0  # 對數似然data_size = 0  # 數據量# 不計算梯度with torch.no_grad():for batch_x, batch_y in dl:  # 遍歷數據加載器# 調用模型的DRL函數計算當前批次的D、R、LDx, Rx, Lx = model.DRL(batch_x.to(device), sample_size=sample_size)# 累加結果D = D + Dx.sum(0)R = R + Rx.sum(0)L = L + Lx.sum(0)data_size += batch_x.shape[0]  # 更新數據量# 計算平均值D = D / data_sizeR = R / data_sizeL = L / data_sizereturn {'ELBO': (-D - R).item(), 'D': D.item(), 'R': R.item(), 'L': L.item()}# 訓練VAE模型的函數。
def train_vae(model: NVIL, opts: OptCollection, training_data, dev_data,batch_size=64, num_epochs=10, check_every=10,sample_size_training=1,sample_size_eval=10,grad_clip=5.,num_workers=2,device=torch.device('cuda:0')):"""訓練VAE模型的函數。參數:- model: PyTorch模型- opts: 優化器集合OptCollection- training_data: 訓練數據- dev_data: 開發/驗證數據- batch_size: 批大小- num_epochs: 訓練周期數- check_every: 每隔多少步檢查一次開發集上的性能- sample_size_training: 訓練時的樣本大小- sample_size_eval: 評估時的樣本大小- grad_clip: 梯度裁剪閾值- num_workers: 使用的工作進程數- device: 運行實驗的設備返回:- 訓練過程中計算的數量的日志（用于繪圖）"""# 創建訓練和開發數據的數據加載器batcher = DataLoader(training_data, batch_size, shuffle=True, num_workers=num_workers, pin_memory=True)dev_batcher = DataLoader(dev_data, batch_size, num_workers=num_workers, pin_memory=True)# 初始化日志記錄器和其他變量total_steps = num_epochs * len(batcher)log = defaultdict(list)# 訓練循環step = 0# 評估模型在開發集上的性能model.eval()for k, v in assess(model, sample_size_eval, dev_batcher, device=device).items():log[f"dev.{k}"].append((step, v))# 使用tqdm顯示進度條with tqdm(range(total_steps)) as bar:for epoch in range(num_epochs):for batch_x, batch_y in batcher:# 設置模型為訓練模式model.train()# 零化梯度opts.zero_grad()# 計算損失字典loss_dict = model(batch_x.to(device), sample_size=sample_size_training,)# 記錄訓練損失for metric, value in loss_dict.items():log[f'training.{metric}'].append((step, value))# 反向傳播loss_dict['loss'].backward()# 梯度裁剪nn.utils.clip_grad_norm_(model.parameters(), grad_clip)    # 更新優化器opts.step()# 更新進度條bar_dict = OrderedDict()for metric, value in loss_dict.items():bar_dict[f'training.{metric}'] = f"{loss_dict[metric]:.2f}"for metric in ['ELBO', 'D', 'R', 'L']:bar_dict[f"dev.{metric}"] =  "{:.2f}".format(log[f"dev.{metric}"][-1][1])bar.set_postfix(bar_dict)bar.update()# 定期在開發集上評估模型if step % check_every == 0:model.eval()for k, v in assess(model, sample_size_eval, dev_batcher, device=device).items():log[f"dev.{k}"].append((step, v))step += 1# 訓練結束后，再次評估模型在開發集上的性能model.eval()for k, v in assess(model, sample_size_eval, dev_batcher, device=device).items():log[f"dev.{k}"].append((step, v))return log# 用于檢查樣本的函數，例如檢查VAE生成的樣本。
def inspect_discrete_lvm(model, dl, device):for x, y in dl:    # 生成先驗樣本x_ = model.sample(16, 4, oversample=True).cpu().reshape(-1, 1, 64, 64)plt.figure(figsize=(12,6))plt.axis('off')plt.imshow(make_grid(x_, nrow=16).permute((1, 2, 0)))    plt.title("先驗樣本")plt.show()# 顯示觀測樣本plt.figure(figsize=(12,6))plt.axis('off')plt.imshow(make_grid(x, nrow=16).permute((1, 2, 0)))    plt.title("觀測")plt.show()# 生成條件樣本x_ = model.cond_sample(x.to(device)).cpu().reshape(-1, 1, 64, 64)plt.figure(figsize=(12,6))plt.axis('off')plt.imshow(make_grid(x_, nrow=16).permute((1, 2, 0)))    plt.title("條件樣本")plt.show()break

3.5.2 方差縮減技巧

以下是一些用于減少方差的實用策略，如果這是您首次接觸這些概念，可以選擇先跳過。

class CentredReward(VarianceReduction):"""這個控制變量沒有可訓練的參數，它維護一個平均獎勵的運行估計，并通過對獎勵計算 reward - avg 來更新一批獎勵。"""def __init__(self, alpha=0.9):super().__init__()  # 調用父類的構造函數self._alpha = alpha  # 衰減系數self._r_mean = 0.  # 初始化平均獎勵def forward(self, r, x=None, q=None, r_fn=None):"""使獎勵居中并更新平均值的運行估計。"""        with torch.no_grad():  # 不計算梯度r_mean = torch.mean(r, dim=0)  # 計算獎勵的均值r = r - self._r_mean  # 居中獎勵self._r_mean = (1-self._alpha) * self._r_mean + self._alpha * r_mean.item()  # 更新平均獎勵估計return r, torch.zeros_like(r)  # 返回居中后的獎勵和零向量class ScaledReward(VarianceReduction):"""這個控制變量沒有可訓練的參數，它維護一個獎勵的標準差的運行估計，并通過計算 reward / max(stddev, 1) 來更新一批獎勵。"""def __init__(self, alpha=0.9):super().__init__()self._alpha = alphaself._r_std = 1.0  # 初始化標準差def forward(self, r, x=None, q=None, r_fn=None):"""通過運行估計的標準差來縮放獎勵，并同時更新估計。"""        with torch.no_grad():r_std = torch.std(r, dim=0)  # 計算獎勵的標準差r = r / self._r_std  # 標準化信號self._r_std = (1-self._alpha) * self._r_std + self._alpha * r_std.item()  # 更新標準差估計self._r_std = np.maximum(self._r_std, 1.)  # 確保縮放因子至少為1return r, torch.zeros_like(r)class SelfCritic(VarianceReduction):"""這個控制變量沒有可訓練的參數，它通過計算 reward - reward' 來更新一批獎勵，其中 reward' 是評估新的樣本 z' ~ Z|X=x 時的 (log p(X=x|Z=z')).detach()。"""def __init__(self):super().__init__()        def forward(self, r, x, q, r_fn):"""標準化獎勵并更新運行估計的均值/標準差。"""with torch.no_grad():z = q.sample()  # 從分布中采樣zr = r - r_fn(z, x)  # 更新獎勵return r, torch.zeros_like(r)class Baseline(VarianceReduction):"""一個輸入依賴的基線，實現為一個多層感知器（MLP）。通過均方誤差調整可訓練參數。"""def __init__(self, num_inputs, hidden_size, p_drop=0.):super().__init__()self.baseline = nn.Sequential(FlattenImage(),  # 將圖像展平nn.Dropout(p_drop),nn.Linear(num_inputs, hidden_size),nn.ReLU(),nn.Dropout(p_drop),nn.Linear(hidden_size, 1)  # 輸出一個值)def forward(self, r, x, q=None, r_fn=None):"""返回 r - baseline(x) 和基線的損失。"""r_hat = self.baseline(x)  # 計算基線預測r_hat = r_hat.squeeze(-1)  # 壓縮維度loss = (r - r_hat)**2  # 計算損失return r - r_hat.detach(), loss  # 返回更新后的獎勵和損失class CVChain(VarianceReduction):"""控制變量鏈，可以串聯多個控制變量。"""def __init__(self, *args):super().__init__()# 添加模塊到當前類if len(args) == 1 and isinstance(args[0], OrderedDict):for key, module in args[0].items():self.add_module(key, module)else:for idx, module in enumerate(args):self.add_module(str(idx), module)def forward(self, r, x, q, r_fn):         loss = 0  # 初始化損失for cv in self._modules.values():  # 遍歷所有控制變量r, l = cv(r, x=x, q=q, r_fn=r_fn)  # 更新獎勵和損失loss = loss + l  # 累加損失return r, loss  # 返回更新后的獎勵和總損失

3.5.3.實驗

# 設置隨機種子以確保結果的可復現性（雖然這里沒有直接顯示seed_all()的具體實現）  
seed_all()  # 創建一個NVIL（神經變分推斷和學習）模型  
# NVIL模型由聯合分布（JointDistribution）、推理模型（InferenceModel）和方差縮減策略（VarianceReduction）組成  
model = NVIL(  # 聯合分布：由BernoulliPriorNet（先驗網絡）和BinarizedImageModel（二值化圖像模型）組成  JointDistribution(  # 先驗網絡，用于生成10維的潛在變量  BernoulliPriorNet(10),  # 圖像模型，它接收10維的潛在變量作為輸入，并預測與給定圖像尺寸相對應的圖像分布  BinarizedImageModel(  num_channels=img_shape[0],  # 圖像通道數  width=img_shape[1],         # 圖像寬度  height=img_shape[2],        # 圖像高度  latent_size=10,             # 潛在變量的大小  p_drop=0.1                  # dropout的概率  )  ),  # 推理模型，用于近似后驗分布  InferenceModel(  latent_size=10,                # 潛在變量的大小  num_channels=img_shape[0],     # 圖像通道數  width=img_shape[1],            # 圖像寬度  height=img_shape[2],           # 圖像高度  cpd_net_type=BernoulliCPDNet   # 控制變分分布的網絡類型  ),  # 方差縮減策略：這里暫時沒有使用任何方差縮減策略  VarianceReduction(), # 不使用方差縮減  # 在NVIL論文中，他們使用了以下方差縮減策略：  # CVChain(  #     CentredReward(),        # 中心化獎勵  #     #Baseline(np.prod(img_shape), 512), # 如果你使用訓練過的基線，可以這樣使用  #     #ScaledReward()         # 縮放獎勵  # )  
).to(my_device)  # 將模型移動到指定的設備（如GPU）  # 創建優化器集合  
# 對于生成模型的參數和推理模型的參數，我們分別使用RMSprop優化器  
opts = OptCollection(  opt.RMSprop(model.gen_params(), lr=5e-4, weight_decay=1e-6),  # 生成模型的參數  opt.RMSprop(model.inf_params(), lr=1e-4),                    # 推理模型的參數  # 如果你使用的基線具有可訓練的參數，你需要為這些參數也設置一個優化器  # opt.RMSprop(model.cv_params(), lr=1e-4, weight_decay=1e-6) # 你需要這個如果你的基線有可訓練的參數  
)  # 顯示模型的結構或信息（這取決于model對象的實現）  
model

# 初始化日志記錄器，用于記錄訓練過程中的各種數據。
log = train_vae(# 傳入要訓練的模型。model=model,# 傳入優化器集合，用于更新模型參數。opts=opts,# 傳入訓練數據集。training_data=train_ds, # 傳入驗證數據集，用于評估模型性能。dev_data=val_ds,# 設置批大小，即每次迭代中使用的樣本數量。batch_size=256, # 設置訓練周期數，更多的周期可能有助于模型更好地收斂。num_epochs=3,# 設置檢查頻率，即每隔多少步在驗證集上評估一次模型。check_every=100,# 設置訓練時使用的樣本大小。sample_size_training=1,# 設置評估時使用的樣本大小。sample_size_eval=1,# 設置梯度裁剪的閾值，用于防止梯度爆炸問題。grad_clip=5.,# 設置運行模型的設備，例如GPU或CPU。device=my_device
)

# 獲取日志記錄器中所有的鍵名。
log_keys = log.keys()# 根據日志中是否包含'training.cv_loss'鍵，創建一個包含3個或4個子圖的圖形。
# figsize參數設置圖形的大小。
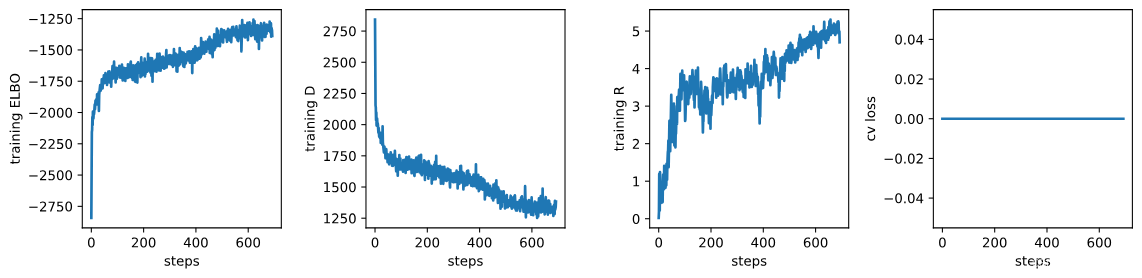
fig, axs = plt.subplots(1, 3 + int('training.cv_loss' in log), sharex=True, sharey=False, figsize=(12, 3))# 繪制訓練過程中的ELBO值。
# 取日志中'training.ELBO'鍵對應的數據，繪制其第一列（步驟）和第二列（ELBO值）。
_ = axs[0].plot(np.array(log['training.ELBO'])[:, 0], np.array(log['training.ELBO'])[:, 1])
# 設置y軸標簽為"training ELBO"。
_ = axs[0].set_ylabel("training ELBO")
# 設置x軸標簽為"steps"。
_ = axs[0].set_xlabel("steps")# 繪制訓練過程中的D值。
_ = axs[1].plot(np.array(log['training.D'])[:, 0], np.array(log['training.D'])[:, 1])
_ = axs[1].set_ylabel("training D")
_ = axs[1].set_xlabel("steps")# 繪制訓練過程中的R值。
_ = axs[2].plot(np.array(log['training.R'])[:, 0], np.array(log['training.R'])[:, 1])
_ = axs[2].set_ylabel("training R")
_ = axs[2].set_xlabel("steps")# 如果日志中包含'training.cv_loss'鍵，則在第四個子圖中繪制控制變量鏈的損失值。
if 'training.cv_loss' in log:_ = axs[3].plot(np.array(log['training.cv_loss'])[:, 0], np.array(log['training.cv_loss'])[:, 1])_ = axs[3].set_ylabel("cv loss")_ = axs[3].set_xlabel("steps")# 使用tight_layout調整子圖布局，h_pad和w_pad參數分別設置水平和垂直間距。
fig.tight_layout(h_pad=1.2, w_pad=1.2)

# 創建一個圖形和4個共享x軸但不共享y軸的子圖。
# figsize參數設置圖形的大小。
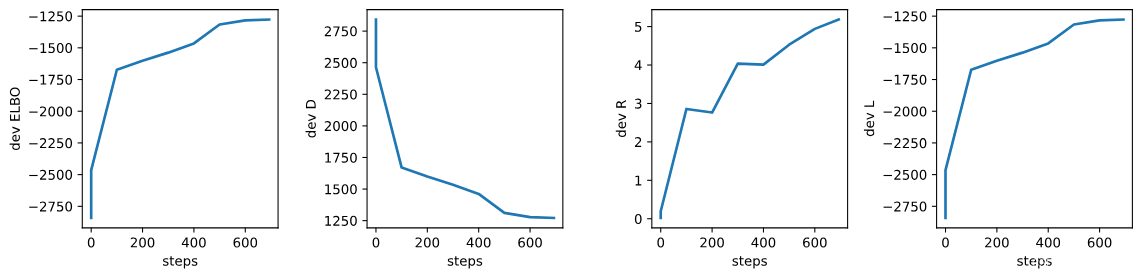
fig, axs = plt.subplots(1, 4, sharex=True, sharey=False, figsize=(12, 3))# 繪制開發集上的ELBO值。
# 取日志中'dev.ELBO'鍵對應的數據，繪制其第一列（步驟）和第二列（ELBO值）。
_ = axs[0].plot(np.array(log['dev.ELBO'])[:, 0], np.array(log['dev.ELBO'])[:, 1])
# 設置第一個子圖的y軸標簽為"dev ELBO"。
_ = axs[0].set_ylabel("dev ELBO")
# 設置第一個子圖的x軸標簽為"steps"。
_ = axs[0].set_xlabel("steps")# 繪制開發集上的D值。
_ = axs[1].plot(np.array(log['dev.D'])[:, 0], np.array(log['dev.D'])[:, 1])
_ = axs[1].set_ylabel("dev D")
_ = axs[1].set_xlabel("steps")# 繪制開發集上的R值。
_ = axs[2].plot(np.array(log['dev.R'])[:, 0], np.array(log['dev.R'])[:, 1])
_ = axs[2].set_ylabel("dev R")
_ = axs[2].set_xlabel("steps")# 繪制開發集上的L值。
_ = axs[3].plot(np.array(log['dev.L'])[:, 0], np.array(log['dev.L'])[:, 1])
_ = axs[3].set_ylabel("dev L")
_ = axs[3].set_xlabel("steps")# 使用tight_layout調整子圖布局，h_pad和w_pad參數分別設置水平和垂直間距。
fig.tight_layout(h_pad=1.2, w_pad=1.2)

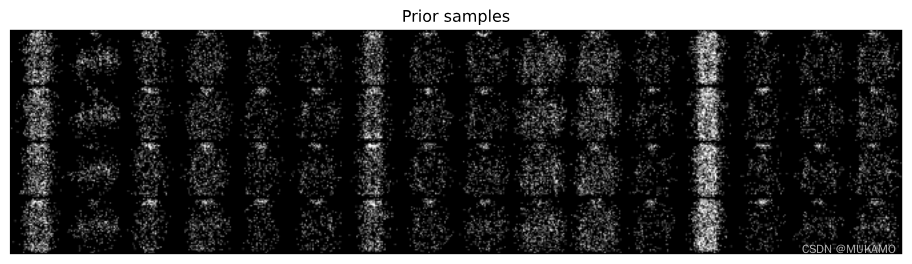
# 調用 inspect_discrete_lvm 函數來檢查或可視化離散潛在變量模型  
# 參數：  
#   model: 模型對象，即已經定義好的離散潛在變量模型  
#   DataLoader(val_ds, 64, num_workers=2, pin_memory=True): 用于加載驗證數據集的數據加載器  
#     val_ds: 驗證數據集  
#     64: 批處理大小（每批加載64個樣本）  
#     num_workers=2: 使用2個工作線程來加載數據  
#     pin_memory=True: 如果在GPU上運行，將數據加載到固定內存中以提高效率  
#   my_device: 設備對象，指定模型應在哪個設備上運行（如 'cuda:0' 表示第一個GPU）  
inspect_discrete_lvm(model, DataLoader(val_ds, 64, num_workers=2, pin_memory=True), my_device)

4. 總結和展望

4.1 總結

本文深入探討了使用深度學習進行概率建模的方法，尤其集中在變分自編碼器（VAE）和神經變分推斷（NVIL）的應用上。從預備知識到模型建立，再到訓練與評估，文章提供了一套完整的流程。

• 預備知識：涵蓋了PyTorch庫的使用、數據預處理、隨機種子設置等基礎操作。
• 模型建立：介紹了如何構建具有離散潛在變量的模型，包括先驗網絡、條件概率分布網絡，以及聯合概率分布模型。
• 訓練流程：討論了最大似然估計和變分推斷兩種方法，以及如何使用優化器更新模型參數。
• 評估與可視化：提供了評估模型性能的方法，并通過Matplotlib對結果進行了可視化展示。

4.2 展望

盡管本文所討論的方法在理論上和實踐上都具有重要意義，但仍有一些潛在的研究方向和應用場景值得進一步探索：

• 模型改進：當前的模型可能在表達能力和泛化性能上有所限制，未來的工作可以探索更復雜的網絡結構或引入新的歸納偏置。
• 算法優化：訓練過程可能需要更高效的算法來加速收斂或提高參數估計的準確性，例如通過改進優化器或引入先進的正則化技術。
• 應用拓展：本文的方法可以應用于更廣泛的領域，如自然語言處理、計算機視覺等，探索這些方法在不同領域的應用將是一個有趣的研究方向。
• 方差縮減技術：本文提到了一些減少方差的技術，但這一領域仍然有待深入研究，以發現更有效的策略來提高訓練過程的穩定性和效率。
• 可擴展性研究：隨著數據規模的增長，研究如何擴展模型以處理大規模數據集也是一個重要的方向。

4.2.1.提高方向

• 你可以嘗試使用連續的輸出分布和CNN編碼器/解碼器。
• 嘗試打開和關閉基線。
• 使用變分推斷（VI），你應該能夠使用更大的$K$值的混合模型，甚至可以與CNN解碼器一起使用。
• 你可以改變數據集（例如，使用SVHN，其圖像是彩色的，因此你將使用3個通道）。
• 你可以嘗試（半）監督潛在編碼（因為這些數據集提供了一定程度的監督）。為此，你可以使用基于模型組件的對數似然旁側損失，該模型組件預測給定潛在編碼的圖像類別的概率質量函數$p_{Y|Z}(y|z,?)$。

參考文獻

本文的撰寫參考了以下文獻和資源，為讀者提供了進一步閱讀和研究的起點：

1. Kingma, D. P., & Welling, M. (2013). Auto-Encoding Variational Bayes. In ICLR.
2. Rezende, D. J., & Mohamed, S. (2014). Variational Inference with Normalizing Flows. In ICML.
3. Goodfellow, I., et al. (2014). Generative Adversarial Networks. In NIPS.
4. Salimans, T., et al. (2015). Markov Chain Monte Carlo without Likelihoods. In ICML.
5. Schulman, J., et al. (2015). Gradient Estimation Using Stochastic Computation Graphs. In ICLR.