介紹

石墨烯算法是一種新興的優化算法，靈感來自于石墨烯的結構和特性。石墨烯是一種由碳原子構成的二維蜂窩狀晶格結構，具有優異的機械、電學和熱學性能。石墨烯算法通過模擬石墨烯原子之間的相互作用和遷移，來求解復雜的優化問題

基本概念

石墨烯的結構：
石墨烯由碳原子組成，每個碳原子與其他三個碳原子通過共價鍵連接，形成一個蜂窩狀的二維晶格結構。這種結構使得石墨烯具有非常高的強度和導電性。

石墨烯算法的靈感：
石墨烯算法借鑒了石墨烯的這種晶格結構和原子遷移特性，通過模擬碳原子在二維平面上的移動和相互作用，來尋找優化問題的最優解

算法步驟

初始化：
初始化一組解，稱為“碳原子”，并將它們隨機分布在二維平面上。這些解代表了問題的初始解集。

評估適應度：
計算每個碳原子的適應度值，根據適應度函數評估每個解的優劣。

更新位置：
根據某種規則更新碳原子的位置，模擬碳原子在二維平面上的遷移。這種遷移可以通過模擬退火、粒子群算法或其他元啟發式方法來實現。

局部搜索：
在每次迭代中，對每個碳原子進行局部搜索，進一步優化其位置。局部搜索可以通過梯度下降或其他局部優化方法來實現。

選擇與替換：
根據適應度值選擇較優的碳原子，并用它們替換較差的碳原子，形成新的解集。

迭代：
重復上述步驟，直到達到預定的迭代次數或滿足收斂條件。

石墨烯算法的優點

全局搜索能力強：
石墨烯算法能夠在廣闊的搜索空間中找到全局最優解，避免陷入局部最優。

收斂速度快：
通過模擬碳原子的快速遷移和局部優化，石墨烯算法具有較快的收斂速度。

適應性強：
石墨烯算法可以處理各種類型的優化問題，包括連續、離散和混合優化問題

石墨烯算法的應用

石墨烯算法可以應用于許多實際問題，如：

工程優化：
用于結構優化、路徑規劃、資源分配等工程領域的問題。

機器學習：
用于神經網絡訓練、特征選擇、超參數優化等機器學習任務。

數據挖掘：
用于聚類分析、關聯規則挖掘、分類等數據挖掘任務。

金融優化：
用于投資組合優化、風險管理、期權定價等金融領域的問題

本文代碼

定義期權定價模型：我們可以使用Black-Scholes模型來計算歐式期權的理論價格。
設計石墨烯優化算法：模擬石墨烯原子之間的相互作用和遷移，以找到最優的期權定價參數。
整合并實現：將期權定價模型和石墨烯算法整合在一起。

期權定價模型（Black-Scholes）

Black-Scholes模型用于計算歐式看漲期權（Call Option）和看跌期權（Put Option）的價格：

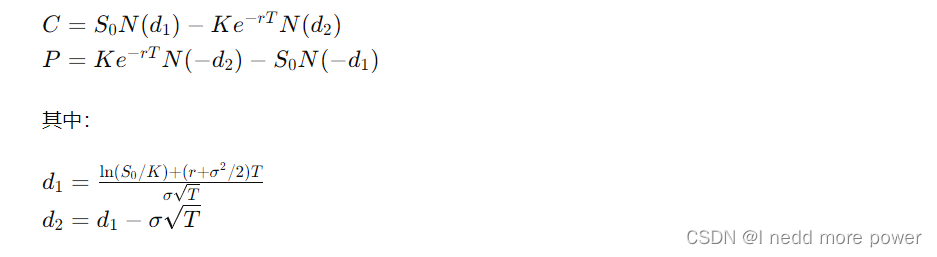
核心代碼

Graphene_Option_Pricing.m

function [best_params, best_fitness] = Graphene_Option_Pricing(S0, K, r, T, market_price, is_call)% 參數初始化dim = 1;  % 需要優化的參數維度：波動率σlower_bound = [0.01];  % 下界：波動率upper_bound = [1.0];  % 上界：波動率max_iter = 500;  % 最大迭代次數pop_size = 30;  % 種群大小% 適應度函數：計算Black-Scholes理論價格與市場價格的均方誤差fitness_func = @(params) calculate_fitness(params, S0, K, r, T, market_price, is_call);% 石墨烯優化算法[best_params, best_fitness] = Graphene_Optimization(dim, lower_bound, upper_bound, max_iter, pop_size, fitness_func);disp('Best parameters found:');disp(best_params);disp('Fitness of best parameters:');disp(best_fitness);% 驗證找到的最佳波動率參數optimal_sigma = best_params(1);% 使用最佳波動率參數計算期權價格if is_callmodel_price = Black_Scholes_Call(S0, K, r, optimal_sigma, T);elsemodel_price = Black_Scholes_Put(S0, K, r, optimal_sigma, T);end% 打印模型價格和市場價格進行比較disp('Optimal sigma:');disp(optimal_sigma);disp('Model option price with optimal sigma:');disp(model_price);disp('Market option price:');disp(market_price);
endfunction fitness = calculate_fitness(params, S0, K, r, T, market_price, is_call)sigma = params(1);if is_callmodel_price = Black_Scholes_Call(S0, K, r, sigma, T);elsemodel_price = Black_Scholes_Put(S0, K, r, sigma, T);end
endfunction C = Black_Scholes_Call(S0, K, r, sigma, T)d1 = (log(S0 / K) + (r + 0.5 * sigma^2) * T) / (sigma * sqrt(T));d2 = d1 - sigma * sqrt(T);C = S0 * normcdf(d1) - K * exp(-r * T) * normcdf(d2);
endfunction P = Black_Scholes_Put(S0, K, r, sigma, T)d1 = (log(S0 / K) + (r + 0.5 * sigma^2) * T) / (sigma * sqrt(T));d2 = d1 - sigma * sqrt(T);P = K * exp(-r * T) * normcdf(-d2) - S0 * normcdf(-d1);
endfunction [best_solution, best_fitness] = Graphene_Optimization(dim, lower_bound, upper_bound, max_iter, pop_size, fitness_func)% 初始化positions = lower_bound + (upper_bound - lower_bound) .* rand(pop_size, dim);% 主循環for iter = 1:max_iter% 更新位置for i = 1:pop_size% 模擬碳原子的遷移new_position = positions(i, :) + rand(1, dim) .* (best_solution - positions(i, :));new_position = max(min(new_position, upper_bound), lower_bound);new_fitness = fitness_func(new_position);% 局部搜索if new_fitness < fitness(i)positions(i, :) = new_position;fitness(i) = new_fitness;end% 更新最優解if new_fitness < best_fitnessbest_fitness = new_fitness;best_solution = new_position;endend% 記錄迭代過程中的最優值（可選）disp(['Iteration ', num2str(iter), ': Best Fitness = ', num2str(best_fitness)]);end
end

run_graphene_option_pricing.m

function run_graphene_option_pricing% 示例使用
S0 = 100;  % 當前股票價格
K = 100;  % 執行價格
r = 0.05;  % 無風險利率
T = 1;  % 到期時間（年）
market_price = 10;  % 市場期權價格
is_call = true;  % 是否為看漲期權[best_params, best_fitness] = Graphene_Option_Pricing(S0, K, r, T, market_price, is_call);
disp('Best parameters for sigma:');
disp(best_params);
disp('Best fitness:');
disp(best_fitness);end

說明

初始化：初始化石墨烯算法的種群，包括參數的上下界、最大迭代次數和種群大小。
適應度函數：計算理論價格和市場價格之間的均方誤差。
Black-Scholes模型：計算歐式看漲期權和看跌期權的價格。
石墨烯優化算法：通過模擬石墨烯原子的遷移和相互作用，找到最佳的期權定價參數。
結果輸出：輸出最佳參數和相應的適應度值。

效果

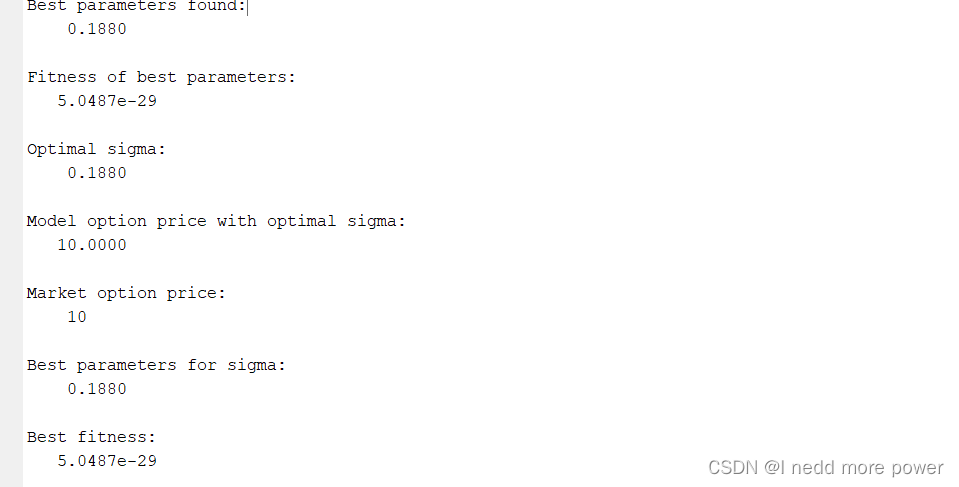
完整代碼獲取

微信掃一掃，回復"石墨烯優化算法"即可查看完整代碼