【Python實戰因果推斷】2_因果效應異質性2

CATE with Regression

Evaluating CATE Predictions

CATE with Regression

我想你可能已經預料到了：與應用因果推理中的大多數情況一樣，答案往往從線性回歸開始。但在走這條路之前，讓我們把事情變得更具體一些。假設你在一家遍布全國的連鎖餐廳工作。這項業務的一個關鍵組成部分是了解何時應該給顧客打折。為此，該公司在全國范圍內進行了一項為期三年的實驗，在連鎖店中的六家不同餐廳隨機提供折扣。數據存儲在以下數據框中：

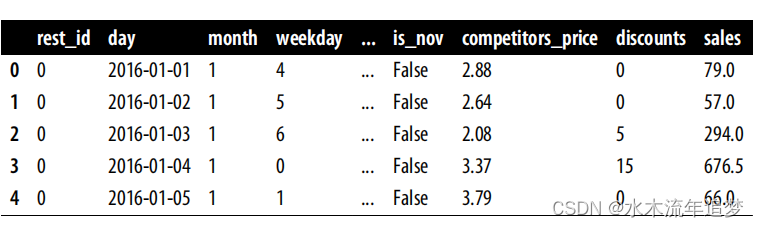您的目標是了解何時是打折的最佳時機。在這些數據中，每家餐廳和每一天都有一行數據。這與本書中使用的大多數示例有些不同，以前的示例以顧客為單位。現在，單位是日-餐廳組合。即便如此，你仍然可以運用以前的推理方法，只是你要 "對待"（給予折扣）的不是顧客，而是 "對待 "日。您也可以在每一天的每家餐廳采用不同的價格，但我們還是把問題簡化為保持各餐廳的價格一致。

您可以將這一業務問題視為 CATE 估算問題。如果您能創建一個模型，輸出每一天的銷售額對折扣的敏感度以及協變量，即 $\frac\partial{\partial t}E[Sales(t)|X]$ ，那么，您就可以使用該模型來決定何時打折以及打多少折。

現在你有了更具體的東西可以利用，讓我們來看看回歸如何幫助你。回想一下，您當時的情況很復雜。您需要預測 $\frac{\delta Y_{i}}{\delta T_{i}}$ ，但遺憾的是，它是不可觀測的。所以你不能簡單地使用多項式回歸算法，然后將其作為目標。但也許你并不需要觀察? $\frac{\delta Y_{i}}{\delta T_{i}}$ ?來預測它。

例如，假設您對數據擬合了以下線性模型： $y_i=\beta_0+\beta_1t_i+\beta_2X_i+e_i$

如果在治療上加以區分，結果會如下： $\frac{\delta y_i}{\delta t_i}=\beta_1$ ? 即在隨機治療的情況下ATE。

由于可以通過估計前面的模型得到 $\widehat{\beta}_{1}$ ，因此甚至可以說，即使無法觀察到斜率，也可以預測斜率。在這個例子中，預測相當簡單。您預測的是每個人的恒定值 $\widehat{\beta}_{1}$ 。這是件好事，但并不是您想要的。這是 ATE，而不是 CATE。這對您計算何時給予折扣沒有任何幫助，因為每個單位（日和餐廳組合）得到的斜率預測都是一樣的。

要改進它，可以做以下簡單的改變： $y_i=\beta_0+\beta_1t_i+\beta_2X_i+\beta_3t_iX_i+e_i$ ，這樣就可以預測出以下坡度： $\frac{\widehat{\delta y_i}}{\delta t_i}=\widehat{\beta_1}+\widehat{\beta_3}X_i$ 其中， $\beta_3$ 是 X 特征的向量系數！

每個由不同 Xi 定義的實體都會有不同的斜率預測。換句話說，斜率預測會隨著 X 的變化而變化。直觀地說，包含治療與協變因素之間的交互作用可以讓模型了解效果如何隨著這些協變因素的變化而變化。這就是回歸如何為您提供估計 CATE 的方法，即使您無法直接預測它。
理論就講到這里。讓我們來看看如何編寫代碼。首先，您需要定義協變量。在本例中，協變量基本上是日期的特定特征，如月份、星期以及是否是節假日。我還加入了競爭對手的平均價格，因為這可能會影響顧客對每家餐廳折扣的反應。

一旦有了協變量，就需要將它們與治療進行交互。* 運算符就可以做到這一點。它為左側和右側創建一個加法項，再加上一個交互項。例如，a*b 將在回歸中包含 a、b 和 a * b 項。在你的例子中，結果如下：

$sales_i=\beta_0+\beta_1discount_i+\beta_2X_i^\star discount_i+\beta_3X_i+e_i$

import statsmodels.formula.api as smf
X = ["C(month)", "C(weekday)", "is_holiday", "competitors_price"]
regr_cate = smf.ols(f"sales ~ discounts*({'+'.join(X)})",data=data).fit()

估算出模型后，就可以從參數估算值中提取預測斜率：

$\frac{\delta sales_i}{\delta discounts_i}=\widehat{\beta_1}+\widehat{\beta_3}X_i$

其中，β1 是折扣系數，β3 是交互系數向量。您可以直接從擬合模型中提取這些參數，但獲得斜率預測的更簡便方法是使用導數的定義： $\frac{\delta y}{\delta t}=\frac{y(t+\epsilon)-y(t)}{(t+\epsilon)-t}$ ,? $\epsilon$ 趨近0，?您可以用 1 代替 $\epsilon$ ?來近似地理解這一定義： $\frac{\delta y}{\delta t}\approx\hat{y}(t+1)-\hat{y}(t)$ ,?其中 y 由模型預測值給出。由于這是一個線性模型，因此近似值是精確的。

換句話說，您將用模型做出兩個預測：一個通過原始數據，另一個通過原始數據，但處理量增加了一個單位。這兩個預測之間的差異就是您的 CATE 預測。下面是一些代碼：

ols_cate_pred = (regr_cate.predict(data.assign(discounts=data["discounts"]+1))-regr_cate.predict(data))

好了，您有了 CATE 模型及其預測。但仍有一個潛伏的問題：它到底有多好？換句話說，如何評估這個模型？您可能已經知道，比較實際值和預測值在這里是行不通的，因為實際治療效果并不是在單位水平上觀察到的。

Evaluating CATE Predictions

如果您有傳統數據科學的背景，您可能會發現這種 CATE 預測看起來很像常規的機器學習預測，但卻有一個無法在單位層面觀察到的隱秘目標。這意味著，傳統機器學習中使用的大量模型評估技術（如交叉驗證）在這里仍然適用，而其他技術則需要一些調整。

因此，為了保持傳統，我們將數據分為訓練集和測試集。既然有時間維度，那就用它吧。訓練集將包含 2016 年和 2017 年的數據，測試集則包含 2018 年以后的數據：

train = data.query("day<'2018-01-01'")
test = data.query("day>='2018-01-01'")

現在，讓我們重試之前的 CATE 回歸模型，但只使用訓練數據進行估計，并對測試集進行預測：

X = ["C(month)", "C(weekday)", "is_holiday", "competitors_price"]regr_model = smf.ols(f"sales ~ discounts*({'+'.join(X)})",data=train).fit()cate_pred = (regr_model.predict(test.assign(discounts=test["discounts"]+1))-regr_model.predict(test))

為了增加趣味性，讓我們用一個純粹的預測性機器學習模型來衡量這個回歸模型。這個機器學習模型只是試圖預測結果 Y：

from sklearn.ensemble import GradientBoostingRegressorX = ["month", "weekday", "is_holiday", "competitors_price", "discounts"]y = "sales"np.random.seed(1)ml_model = GradientBoostingRegressor(n_estimators=50).fit(train[X],train[y])ml_pred = ml_model.predict(test[X])

最后，讓我們把一個非常糟糕的模型也納入比較范圍。這個模型簡單地輸出-1 和 1 之間的隨機數。這顯然是無稽之談，但也是一個值得關注的有趣基準。歸根結底，你想知道用 CATE 模型分配治療是否會比隨機分配更好，這就是最后一個模型的作用。

為了方便起見，我將所有數據存儲在一個新的數據幀 test_pred：

np.random.seed(123)test_pred = test.assign(ml_pred=ml_pred,cate_pred=cate_pred,rand_m_pred=np.random.uniform(-1, 1, len(test)),)

有了模型之后，就該想辦法評估和比較它們了。也就是說，你必須面對ground truth是不可觀測的這一事實。正如你很快就會看到的，訣竅在于認識到，盡管你無法測量單個個體的治療效果，但你可以估計很小群體的治療效果。因此，如果你想用 CATE 來評估你的模型，就必須依賴于群體層面的指標。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/diannao/35992.shtml
繁體地址，請注明出處：http://hk.pswp.cn/diannao/35992.shtml
英文地址，請注明出處：http://en.pswp.cn/diannao/35992.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！