1、主要解決問題類型

1.1 預測分析（Prediction）

線性回歸可以用來預測一個變量（通常稱為因變量或響應變量）的值，基于一個或多個輸入變量（自變量或預測變量）。例如，根據房屋的面積、位置等因素預測房價。

1.2 異常檢測（Outlier Detection）

線性回歸可以幫助識別數據中的異常值。異常值可能會影響回歸模型的準確性，因此檢測和處理異常值是線性回歸分析的重要一環。

1.3 關聯分析（Association）

線性回歸可以幫助確定兩個或多個變量之間的關系強度和方向。它可以顯示自變量與因變量之間是正相關還是負相關，以及相關性的強度。

2、線性回歸模型

2.1 什么是線性回歸模型

模型表達式：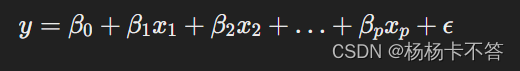

• y 是因變量（要預測的目標）
• x1,x2,…,xp 是自變量（特征或解釋變量）
• β0,β1,…,βp 是模型的參數，表示因變量與自變量之間的影響關系
• ? 是誤差項，表示模型無法解釋的隨機誤差。

2.2 如何判斷某個問題是否適合使用線性回歸模型？

1. 線性關系假設：線性回歸模型假設因變量與自變量之間的關系是線性的。因此，首先需要檢驗自變量和因變量之間是否存在大致的線性關系。可以通過繪制散點圖觀察變量之間的關系來初步判斷。
2. 連續性和正態性假設：線性回歸模型通常假設自變量和因變量是連續的，并且誤差項 ? 是獨立同分布的，并且服從正態分布。如果數據違反這些假設，可能需要考慮其他類型的模型。
3. 數據量：通常來說，線性回歸對數據量的要求并不高，但是如果數據量非常少或者變量之間的關系非常復雜，可能需要考慮更復雜的模型。
4. 預測的需求：如果任務是預測一個連續的數值型目標變量，而且認為這些預測可以通過自變量的線性組合來實現，那么線性回歸也是一個合適的選擇。

2.3 NILM中的線性回歸模型

2.3.1 負載識別問題

在NILM中，負載識別是一個核心問題，即通過總電力消耗數據來識別和分離出各個電器的能耗。線性回歸模型可以應用于以下情況：

問題描述： 根據總電力消耗（因變量）和不同電器的特征（自變量，如電流波形、功率特征等），建立線性回歸模型來預測每個電器的能耗。

實際案例： 假設我們有一個家庭的總電力消耗數據以及每個電器在不同時間段內的功率特征。我們可以利用線性回歸模型來擬合這些數據，從而識別出在該家庭中運行的各種電器，比如冰箱、空調、洗衣機等。

求解過程如下

1. 數據的收集與準備

首先，我們需要收集如下數據：

• 總電力消耗數據： 在監測點（例如家庭電表）上采集的總電力消耗時間序列數據。
• 各個電器的特征數據： 這些特征數據可以包括電器的功率特性、波形數據（如電流波形）、電壓特征等。這些數據通常是通過傳感器或NILM系統采集的。

2. 模型設定

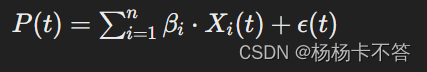
• P(t) 是在時刻 ?? 的總電力消耗
• Xi(t) 是第 ?? 個電器的特征數據，如功率特征
• βi 是模型的系數，表示第 ?? 個電器的能耗
• ?(t) 是誤差項，表示模型無法解釋的隨機誤差。

3. 模型擬合

接下來的步驟是通過擬合模型來估計系數 ????，這里使用最小二乘法來優化模型參數。
假設我們有以下數據：

我們可以將數據集分為訓練集和測試集，然后按照上述步驟建立線性回歸模型。例如，可以使用Python中的Scikit-Learn庫來實現：

from sklearn.linear_model import LinearRegression
import numpy as np# 假設已經有了總電力消耗數據 P 和電器特征數據 X# 創建線性回歸模型
model = LinearRegression()# 擬合模型
model.fit(X, P)# 打印模型系數（電器的能耗）
print("Coefficients (beta):", model.coef_)
print("Intercept (beta_0):", model.intercept_)

4. 模型評估與驗證

完成模型擬合后，需要對模型進行評估和驗證：

• 評估模型擬合度： 通過比較模型預測的總電力消耗與實際觀測值之間的差異來評估模型的擬合度。
• 驗證識別準確性： 使用未見過的數據集來驗證模型的負載識別能力，即模型是否能夠準確識別和分離不同電器的能耗。

2.3.1.1 簡單的負載識別（使用線性回歸模型）

1. 數據準備

• P 是總電力消耗數據，假設是一個長度為 n 的 numpy 數組。
• X1 和 X2 是兩個電器的功率特征數據，每個也是長度為 n 的 numpy 數組。

2. 特征矩陣X的構建

• 使用 np.vstack 將每個電器的特征數據堆疊為一個矩陣，每列對應一個電器的特征數據。
• 使用 .T 進行轉置，以確保每行對應相同時間點的數據。

3. 模型擬合

• 創建 LinearRegression 對象，并使用 fit 方法擬合模型，將 X 作為自變量，P 作為因變量。

4.模型系數

• model.coef_ 返回每個電器的能耗系數（即模型的斜率）。
• model.intercept_ 返回模型的截距項（即 β0）。

代碼實現如下：

import numpy as np
from sklearn.linear_model import LinearRegression# 假設有以下數據：
# 總電力消耗數據 P，假設是一個長度為 n 的 numpy 數組
P = np.array([100, 150, 200, 180, 210])# 電器特征數據 X，假設有兩個電器，每個電器的特征數據也是長度為 n 的 numpy 數組
X1 = np.array([20, 30, 40, 35, 45])  # 電器1的功率特征
X2 = np.array([15, 25, 30, 20, 28])  # 電器2的功率特征# 將電器特征數據整合成一個特征矩陣 X，每一列對應一個電器的特征數據
X = np.vstack([X1, X2]).T  # 轉置是為了確保每行對應同一個時間點的數據# 創建并擬合線性回歸模型
model &#