PID原理及控制算法詳解

文章目錄

1. 概念

1.1 PID框圖

1.2 具體示例：無人機高度控制

2. PID原理

3. 常用術語

4. 計算過程

4.1 比例控制（Proportional）

4.2 積分控制（Integral）

4.3 微分控制（Derivative）

5. 代碼實現邏輯

7. 串級PID和代碼實現

6. 模擬仿真

1. 概念

PID是應用最廣泛的閉環控制方法之一，是一種常用的反饋控制方法，對于每個PID控制器由三個部分組成：比例控制（Proportional）、積分控制（Integral）和微分控制（Derivative）。

一般而言，目標值和反饋值為同種物理量，輸出值可以是施加在被控物體上的控制量
舉例：對物體進行位置控制時，目標值=目標位置，反饋值=當前位置，輸出值=施加的驅動力大小，PID就能實時計算出驅動力使物體到達目標位置。

控制程序一般會定時運行PID算法，在每次運行時，先計算出誤差=目標值-反饋值，然后分別由P、I、D三個環節根據誤差計算出輸出分量，三個分量加和即為最終輸出值。

1.1 PID框圖

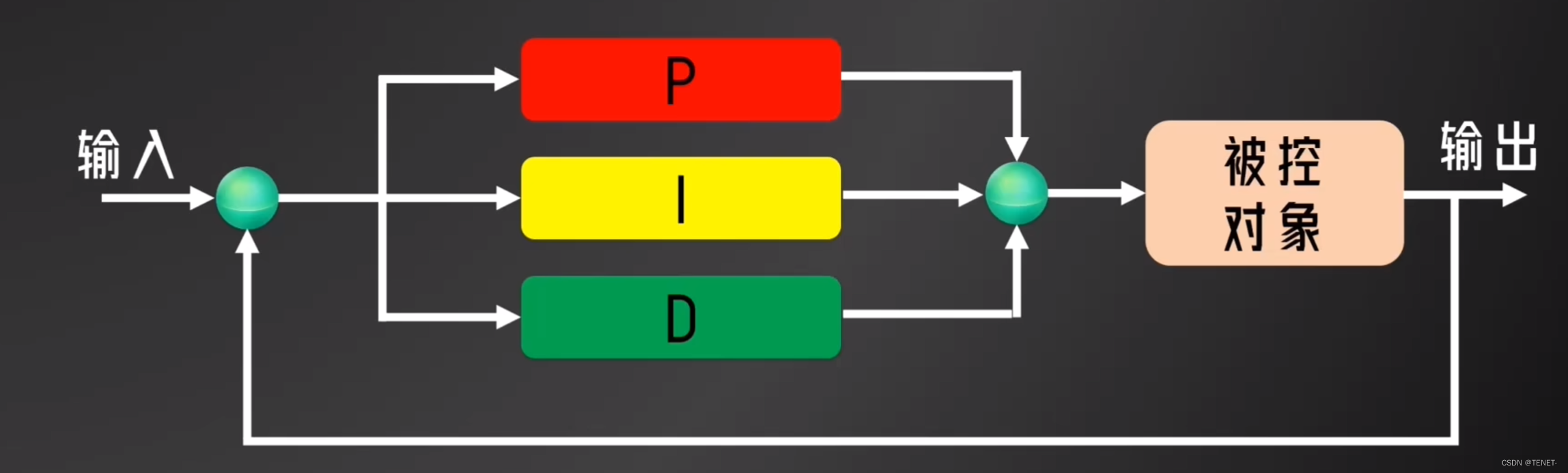
上圖就是PID的信號框圖，表示了PID的運行過程：

為系統指定一個目標值。PID將目標值與被控對象（無人機）當前的反饋量作差得到誤差。PID將誤差值分別經過三個環節計算得到輸出分量，三個分量加起來得到PID的輸出。將PID的輸出施加到被控對象上，使反饋量向目標值靠攏。

PID三個環節的作用

由控制無人機案例我們可以總結出PID三個環節各自的主要作用和效應：

比例環節：起主要控制作用，使反饋量向目標值靠攏，但可能導致振蕩。
積分環節：消除穩態誤差，但會增加超調量。
微分環節：產生阻尼效果，抑制振蕩和超調，但會降低響應速度。

PID中物理量的設計

我們在設計PID時主要關注三個量：目標值、反饋值、輸出值。PID會根據目標值和反饋值計算輸出值。

需要強調的是，PID并不知道被控對象是什么，它僅負責進行數值計算，而我們——作為控制系統的設計者，就需要為PID指定這三個量所對應的實際物理量，這在不同的控制系統中是不一樣的。

如何確定實際物理量

我為大家總結了一個常用準則：

目標值和反饋值：
- 通常為同種物理量，就是你需要控制的物理量。
輸出值：
- 通常是直接驅動被控對象的控制量。
- 輸出量作用在被控對象上需要經過時間積累才會產生反饋量的變化，換言之，輸出值通常為反饋值對于時間的低階物理量。例如：目標值和反饋值為位置，則輸出值可以為速度或加速度。

對于線性關系的兩個物理量（只差一個系數），可以直接替換。例如：目標和反饋值為無人機的位置，根據上一條準則，輸出值可以為加速度。但我們無法直接控制加速度，只能控制推力大小，由于由于高度的變化是由推力產生的，且推力與加速度只差一個系數（F=ma），因此可以將輸出值直接定為推力。

1.2 具體示例：無人機高度控制

目標值（Setpoint）：無人機希望達到的高度，例如10米。
反饋值（Measured Value）：無人機當前的實際高度，例如8米。
誤差（Error）：
- 目標高度與實際高度的差值。誤差 = 目標高度 - 實際高度 = 10米 - 8米 = 2米。
輸出值（Output）：
- 控制電機的推力大小，以使無人機的高度向目標高度靠攏。
- 由于推力與加速度成正比，我們可以將輸出值設為推力。通過調整推力來改變無人機的加速度，從而改變高度。

2. PID原理

這是一個通過PID控制水管進出水流量的例子。讓我們詳細解釋這個例子：

圖示說明

閥門：水管中間有一個閥門，通過調節閥門的開度來控制水流量。
PID控制器：控制系統通過PID控制器來調節閥門，以控制水流量。
流量傳感器：水管上有流量傳感器，用來測量當前的實際流量。

工作原理

設定值：系統有一個預期流量值（設定值），這是希望達到的水流量。比如2L/S.
測量值：流量傳感器實時測量當前的實際流量。
誤差計算：PID控制器將實際流量與預期流量進行比較，得到誤差值（誤差 = 預期流量 - 實際流量）。
控制輸出：
- 比例控制（P）：根據當前誤差值直接調節閥門的開度。誤差越大，調整幅度越大。
- 積分控制（I）：根據誤差隨時間的累積來調節閥門，以消除持續的偏差。積分控制能消除系統的穩態誤差。
- 微分控制（D）：根據誤差變化的速度來調節閥門，預見并平滑誤差的變化，減少超調和振蕩。

實際操作

啟動時：當系統啟動時，PID控制器根據初始誤差進行較大的調整，使流量迅速接近設定值。
穩定階段：當實際流量接近設定值時，比例控制器的作用減小，積分控制器確保誤差歸零，微分控制器平滑誤差變化，避免波動。
擾動響應：當系統受到外部擾動（如水壓變化）時，PID控制器會重新計算誤差，并調整閥門，以重新達到設定的流量值。

3. 常用術語

被控對象：需要控制的對象。例如，溫度控制中的加熱器、速度控制中的電機等。
目標值（Setpoint）：期望被控對象達到的狀態量。例如，溫度控制中的期望溫度、速度控制中的目標速度。
反饋值（Measured Value）：被控對象當前時刻的狀態量。例如，當前的溫度、當前的速度。
增益（Gain）：比例、積分和微分部分的放大系數，分別是Kp、Ki和Kd。
輸出量（Output）：PID的計算結果，用于調整被控對象的控制力。例如，加熱器的功率、驅動電機的電壓。
誤差（Error）：目標值與反饋值之間的差異。公式為：誤差 = 目標值 - 反饋值。
穩態誤差（Steady-State Error）：系統在穩定狀態下仍然存在的誤差。例如，加入干擾后仍存在的誤差。
階躍輸入（Step Input）：在系統穩定狀態下，目標值發生突然變化。例如，目標溫度從20°C突然升高到25°C。
階躍響應（Step Response）：階躍輸入后，被控對象的響應狀態，能夠代表系統的控制性能。
瞬態響應（Transient Response）：系統從初始狀態到達到穩態的過渡過程，包括上升時間、超調量和調節時間等。
響應速度（Response Speed）：階躍輸入后，被控對象再次到達目標值的速度。
超調量（Overshoot）：階躍輸入后，被控對象到達目標值后超出目標值的距離。

4. 計算過程

這里用無人機的高度控制來舉例

4.1 比例控制（Proportional）

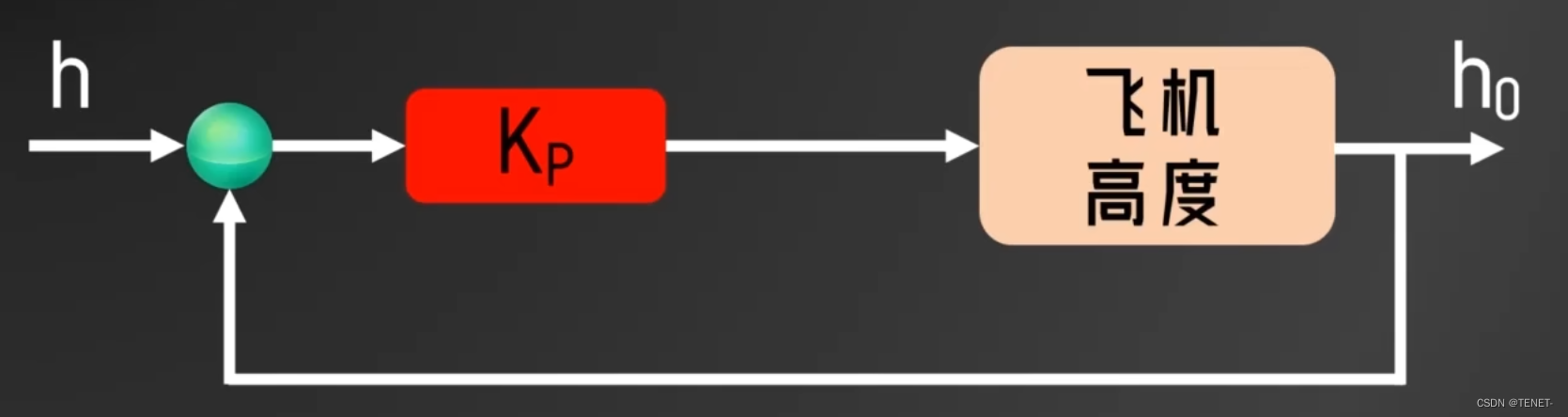
假如讓無人機懸停在10米的高度，但此時高度為2米，所以此時誤差(error)為8米，假設Kp=0.5，比例控制每次調節的高度就為：

Kp * error

所以第一次調節為 0.5*8=4，此時誤差變為4米。

第二次調節：0.5*4=2，此時誤差變為2米。

依次進行調節，誤差逐漸變小。這個過程就叫做比例調節。

Kp值越大，系統反應速度越快，無人機更快靠近誤差。

但是比例控制的缺點為兩點：

干擾：容易受到外界干擾，比如此時有持續的風將無人機向下吹，導致無人機同一周期向下1米，此時比例控制的計算結果為0.5*2=1，所以，這會導致無人機永遠保持在八米的高度，誤差保持在2米。這也叫做穩態誤差。
震蕩：Kp值越大，系統反應速度越快，無人機更快靠近誤差，但同時無人機在接近目標高度時，產生的震蕩也越嚴重。

為了消除穩態誤差的問題，就需要用到積分控制（Integral）。

為了消除系統震蕩的問題，就需要用到微分控制（Derivative）。

4.2 積分控制（Integral）

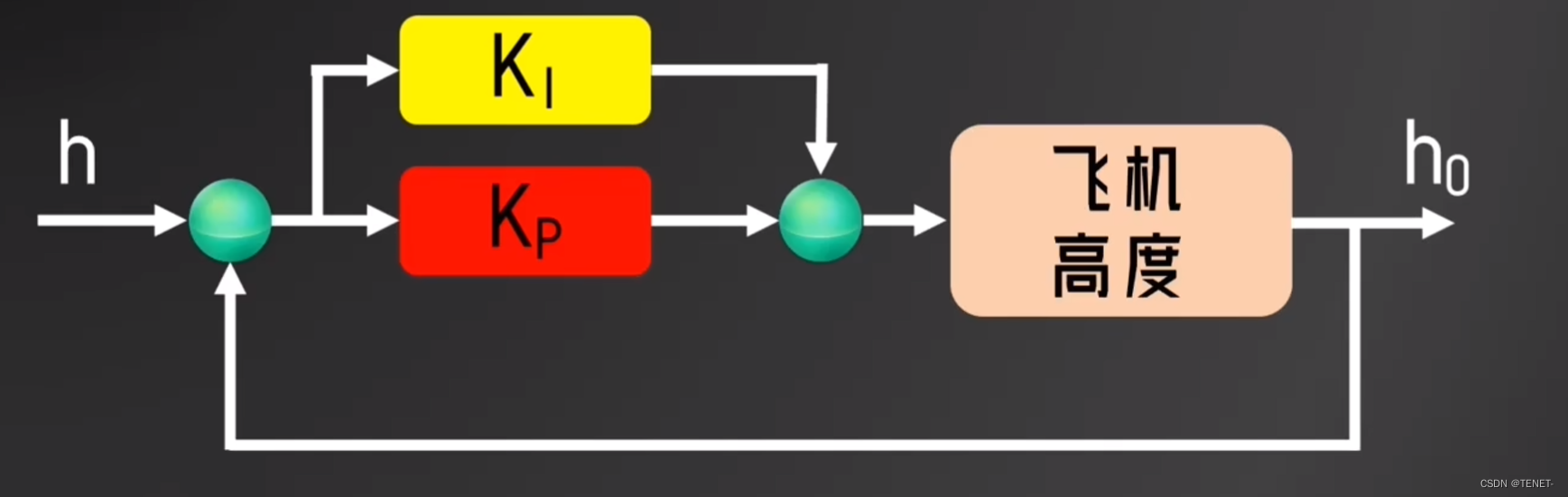
積分控制是對之前計算的所有的誤差求和，也就是在離散的情況下做累加，比如無人機經過兩次調節，第一次誤差為8米，第二次誤差為4米，加起來就是12米，假如Ki=0.1，計算結果為：

?0.1*12=1.2，所以及時有向下持續的風影響無人機，由于積分控制，無人機還是會向上走1.2米。

所以積分控制會對誤差進行累計，從而提供更大的升力，讓無人機慢慢的朝著目標點靠近，最終誤差消除為0。

所以經過第三次調節，累計誤差從12調整到了12.8，那么第四次調節的結果0.1*12.8=1.28。

但此時無人機距離目標高度僅為0.8米，如果還是調節1.28米，就會出現過沖現象。

此時就需要使用微分控制進行更細致的調節。

4.3 微分控制（Derivative）

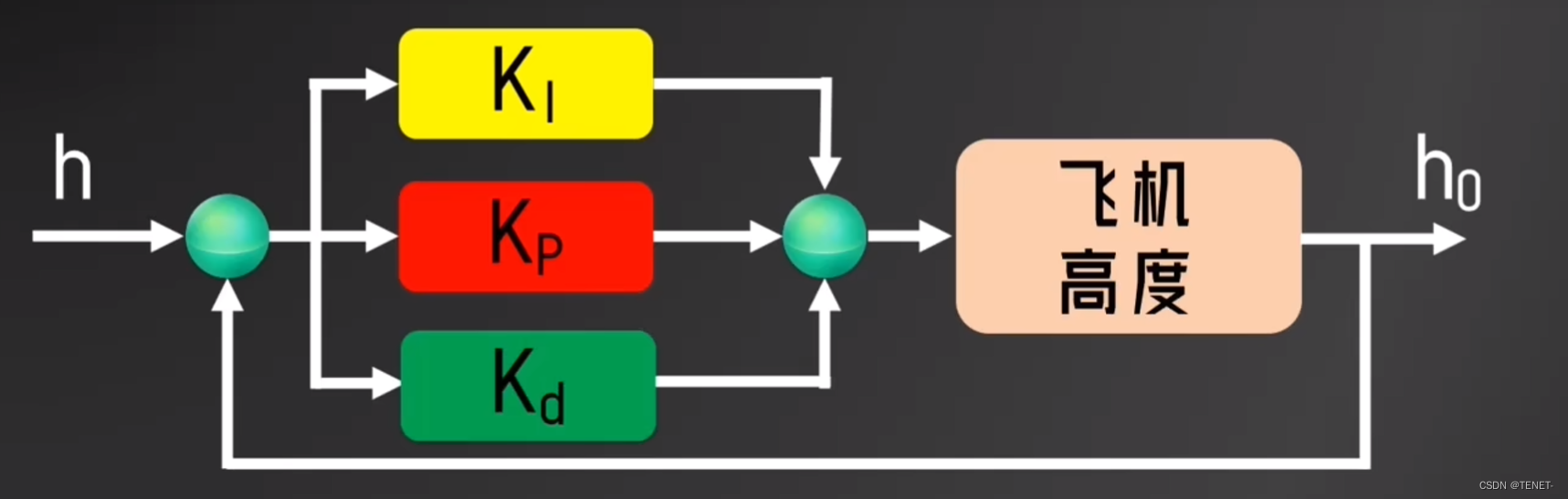
微分控制就是通過當前時刻與前一刻誤差量的差值對未來做預測。如果差值為正，就表示誤差在變大，為負就表示誤差在減小。如果誤差在變大，就會加大控制強度，讓誤差降下來。如果誤差減小，就會減小控制強度，讓無人機平穩緩和的到達指定值。

這里也就相當于對距離求微分：

d(error)/dt = 速度

微分控制算法可以對無人機的速度做出響應，當無人機的速度過快時，微分控制會抵消一部分由比例控制計算出來的升力，從而減緩系統的震蕩。所以當我們提高Kd的值，系統的震蕩會逐步減小。

但無論是比例，積分還是微分控制，數值調的過大，無人機就會出現過沖現象。

5. 代碼實現邏輯

這段偽代碼實現了一個基本的PID控制算法。

previous_error := 0
integral := 0loop:error := setpoint - measured_value //計算誤差integral := integral + error * dt //計算積分derivative := (error - previous_error) / dt //計算微分output := Kp * error + Ki * integral + Kd * derivative //計算控制輸出previous_error := error //更新前一次誤差wait(dt) //等待并循環goto loop