1. 堆的基本了解

? ? ? ? 堆（heap）是計算機科學中一種特殊的數據結構，通常被視為一個完全二叉樹，并且可以用數組來存儲。堆的主要應用是在一組變化頻繁（增刪查改的頻率較高）的數據集中查找最值。堆分為大根堆和小根堆，大根堆中任意節點的值都大于其子樹中節點的值，而小根堆則相反。堆的存儲方式遵循層序遍歷的規則，這樣可以高效地利用存儲空間。在數組中，根節點的下標為0，節點的左右孩子的下標可以通過特定的公式計算得出。堆的實現通常利用動態數組，這樣可以快速擴展容量而不造成空間浪費。

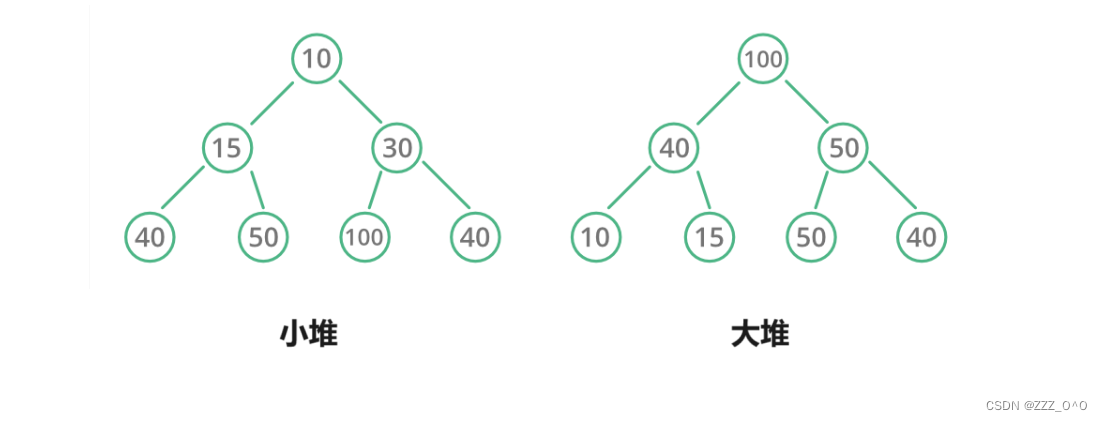
堆的一些性質：1.堆中某個結點的值總是不大于或不小于其父結點的值；

? ? ? ? ? ? ? ? ? ? ? ? ?2.堆總是一棵完全二叉樹。

2. 堆的實現

?我們知道堆的邏輯結構是一個完全二叉樹，但是其物理結構仍然是一個數組，所以實現堆創建一個數組即可。

typedef int HPDateType;typedef struct Heap
{HPDateType* a;int size;int capacity;
}HP;void HPInit(HP* php)
{assert(php);php->a = NULL;php->capacity = php->size = 0;
}
void HPDesTroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}void Swap(HPDateType* p1, HPDateType* p2)
{HPDateType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDateType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[child]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HPPush(HP* php, HPDateType x)
{if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDateType* tmp = (HPDateType*)realloc(php->a, sizeof(HPDateType) * newcapacity);if (tmp = NULL){perror("realloc");return;}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}
void AdjustDown(HPDateType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void HPPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}HPDateType HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}

2.1 堆的插入

大堆的父節點均大于子節點，小堆恰好相反，自然實現邏輯各不相同，這里主要有兩個主要的思想就是"父子值交換"，"父子址交換"。解釋就是（以小堆為例）：

如果對一個已有的小堆插入新的數據（葉子），如果這個葉子與他的父節點相比更小，就與父節點交換，再與交換后節點所屬的父節點對比，如果還是小于就繼續交換。

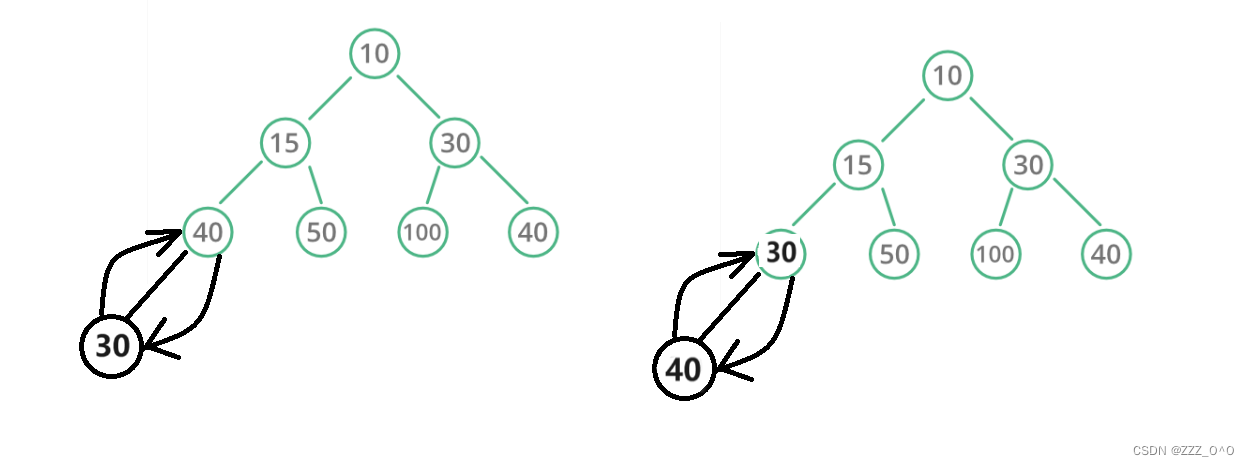
?代碼解釋如下：?

當要插入數據時先將其放在葉子節點（數組尾部），通過AdjustUp函數可以實現向上比較的動作，當然插入前判斷空間是否充足，適當擴容即可。

void AdjustUp(HPDateType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[child]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HPPush(HP* php, HPDateType x)
{if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDateType* tmp = (HPDateType*)realloc(php->a, sizeof(HPDateType) * newcapacity);if (tmp = NULL){perror("realloc");return;}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}

2.2 堆的刪除

堆的刪除就是將根節點與葉子節點交換后直接刪除交換后的葉子節點（即最初的跟節點數據），然后將交換后的根節點逐漸向下交換，如圖所示：

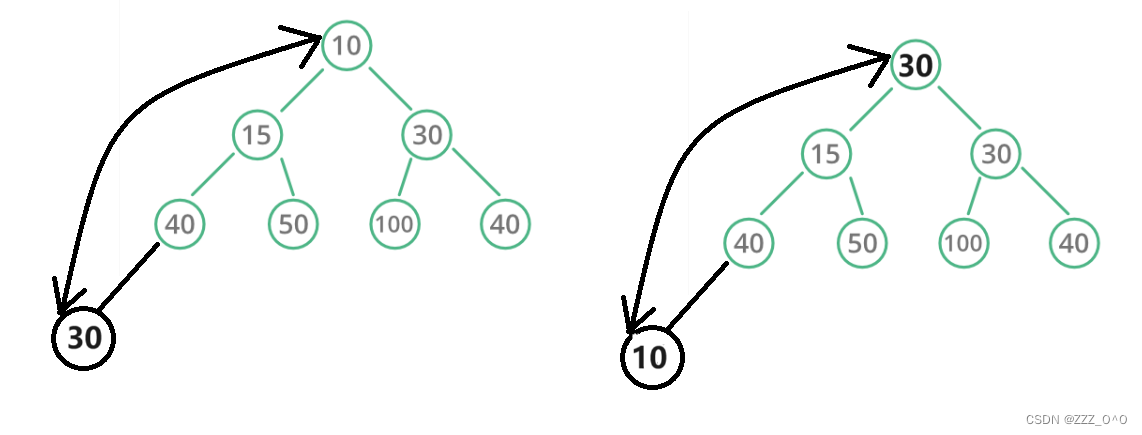
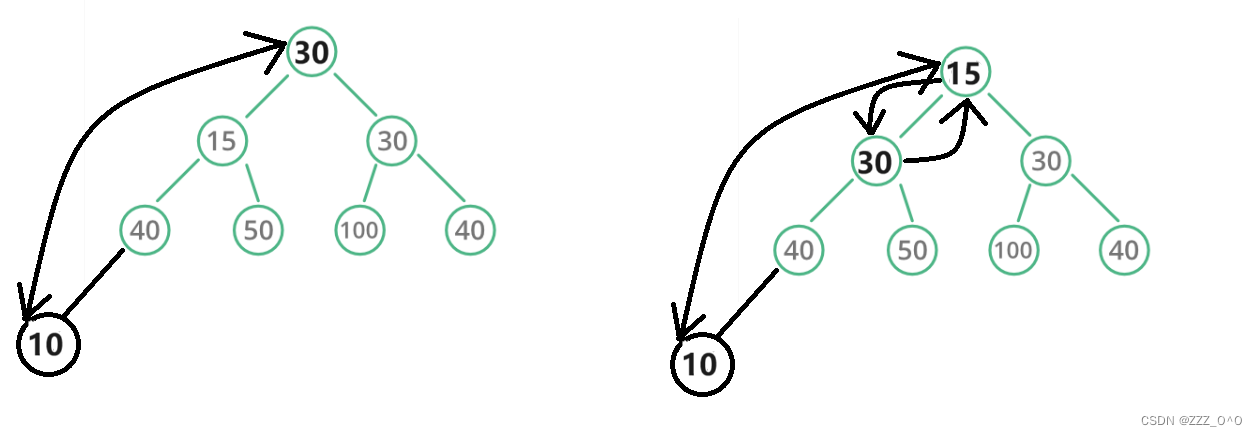?通過代碼展示就是，先交換根節點與葉子結點（即數組頭尾交換）然后直接刪除交換后的葉子結點。創建一個AdjustDown函數，逐層下沉交換后的跟節點，保持仍然是一個堆。

void AdjustDown(HPDateType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void HPPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}

3.堆排序

主要思路：升序建大堆，降序建小堆

解釋：以升序為例，創建一個大堆，即根節點為最大的數據，此時要排序，就直接將根節點與葉子結點交換（數組首尾交換），然后數組末尾的下標向前移動（此時數組末尾的數據不會參與后續運算），然后將交換后的跟節點使用AdjustDown函數下沉，以此類推，最后原數組就是一個升序排列。同理小堆也是如此。

為什么升序不用小堆呢，因為小堆每一次運算都要再次創建一個數組，浪費更多的內存，可以使用但是不推薦。同理這也是為什么降序使用小堆。

具體代碼如下

void HeapSort(int* a, int n)
{// 降序，建小堆// 升序，建大堆for (int i = 1; i < n; i++){AdjustUp(a, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}