6.2.2 快速排序

【問題】快速排序(quick?sort)的分治策略如下（圖6-5)。
(1)劃分：（選定一個記錄作為軸值，以軸值為基準將整個序列劃分為兩個子序列，軸值的位置在劃分的過程中確定，并且左側子序列的所有記錄均小于或等于軸值，右側子序列的所有記錄均大于或等于軸值。
(2)?求解子問題：分別對劃分后的每一個子序列進行遞歸處理。
(3)?合并：由于對子序列的排序是就地進行的，所以合并不需要執行任何操作。

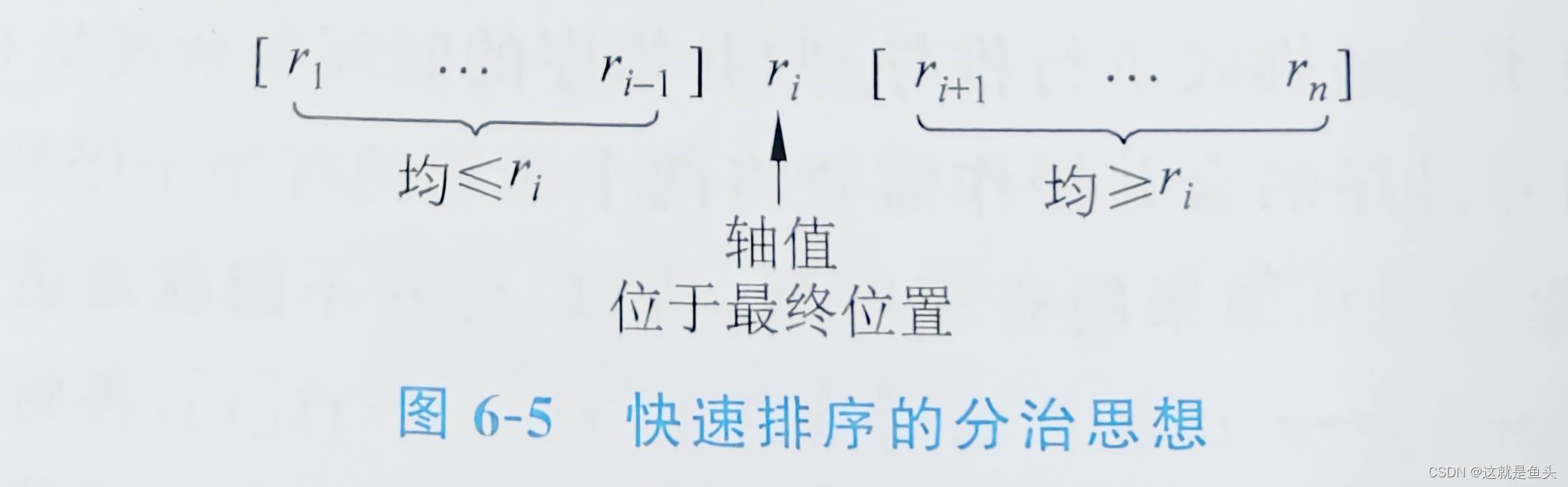
【想法】首先對待排序記錄序列進行劃分，刻分的軸值應該遵循平衡子問題的原則，使劃分后兩個子序列的長度盡量相等。軸值的選擇有很多方法，例如，可以隨機選出一個記錄作為軸值，從而期望劃分是較平衡的。假設以第一個記錄作為軸值，圖6-6給出了、個劃分的例子（黑體框代表軸值）。

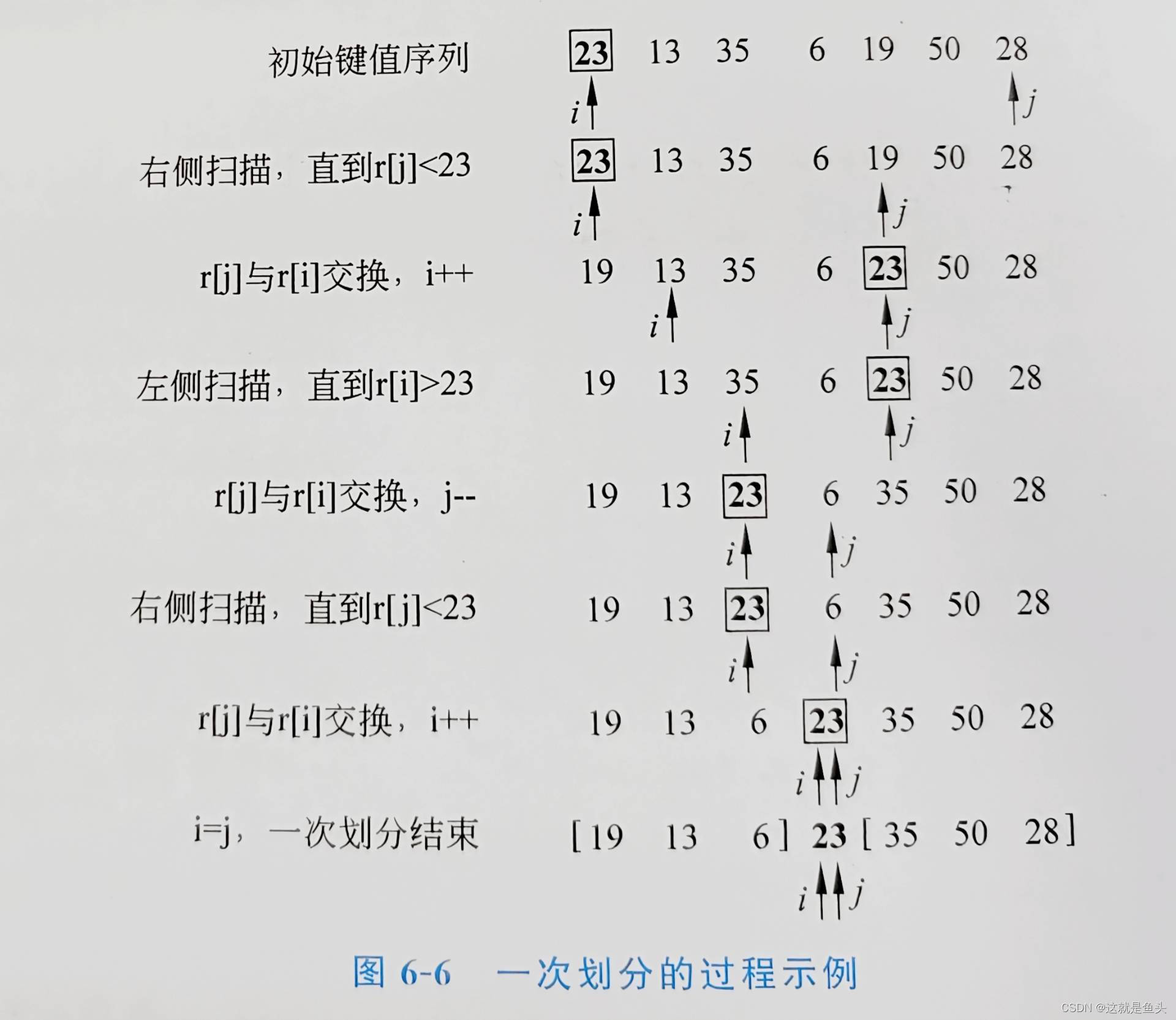
????????以軸值為基準將待排序序列劃分為兩個子序列后，對每一個子序列分別進行遞歸處理。圖6-7所示是一個快速排序的完整的例子。

【算法實現】設函數Partition實現對序列r[first]~r[end]進行劃分，函數QuickSort實現快速排序，程序如下。

#include <iostream>
using namespace std;

int Partition(int r[ ], int first, int end)
{
int temp, i = first, j = end;
while (i < j)
{
while (i < j && r[i] <= r[j]) j--; //右側掃描
if (i < j)
{
temp = r[i]; r[i] = r[j]; r[j] = temp; //將較小記錄交換到前面
i++;
}
while (i < j && r[i] <= r[j]) i++; //左側掃描
if (i < j)
{
temp = r[i]; r[i] = r[j]; r[j] = temp; //將較大記錄交換到后面
j--;
}
}
return i; //返回軸值記錄的位置
}

void QuickSort(int r[ ], int first, int end) //快速排序
{
if (first < end)
{
int pivot = Partition(r, first, end); //劃分，pivot是軸值的位置
QuickSort(r, first, pivot-1); //對左側子序列進行快速排序
QuickSort(r, pivot+1, end); //對右側子序列進行快速排序
}
}
int main( )
{
int i, n = 8, r[8] = {8,3,2,6,7,1,5,4};
? ? QuickSort(r, 0, n-1);

? ? for (i = 0; i < n; i++)
? ? ? ? std::cout << r[i] << " "; ?// 打印排序后的元素

? ? std::cout << std::endl;

? ? return 0;
}
?

【算法分析】?最好情況下，每次劃分對一個記錄定位后，該記錄的左側子序列與右側子序列的長度相同。在具有n個記錄的序列中，一次劃分需要對整個待劃分序列掃描一遍，所需時間為O(n),則有：

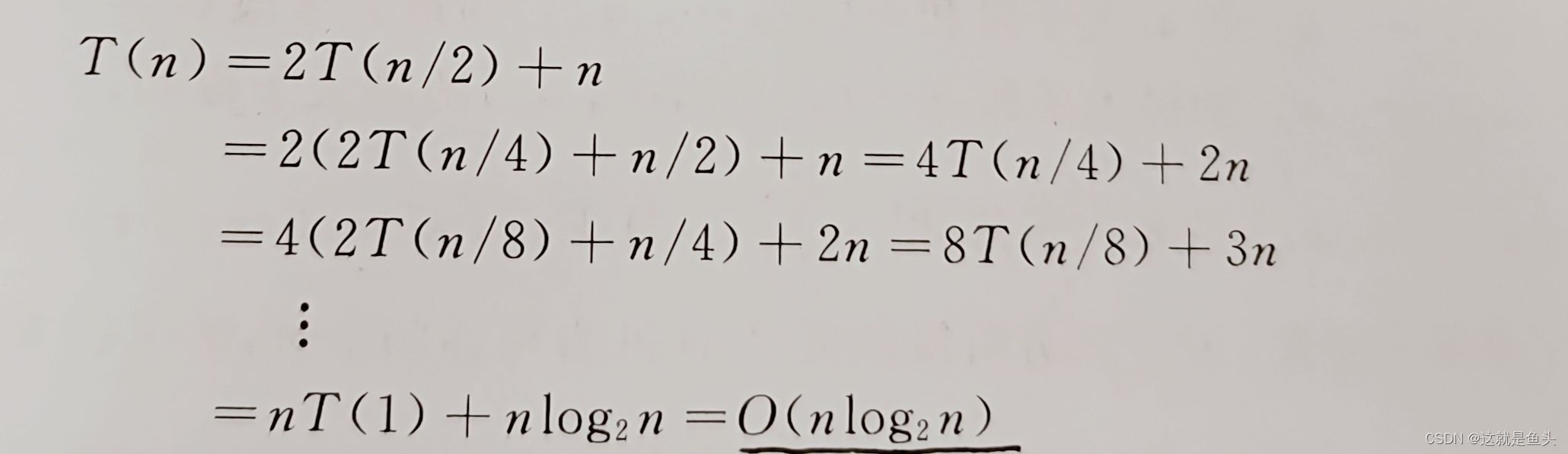
????????最壞情況下，待排序記錄序列正序或逆序，每次劃分只得到一個比上一次劃分少一個記錄的子序列（另一個子序列為空）。此時，必須經過n-1次遞歸調用才能把所有記錄定位，而且第i趟劃分需要經過n-i次比較才能找到第i個記錄的位置，因此，時間復雜度為：

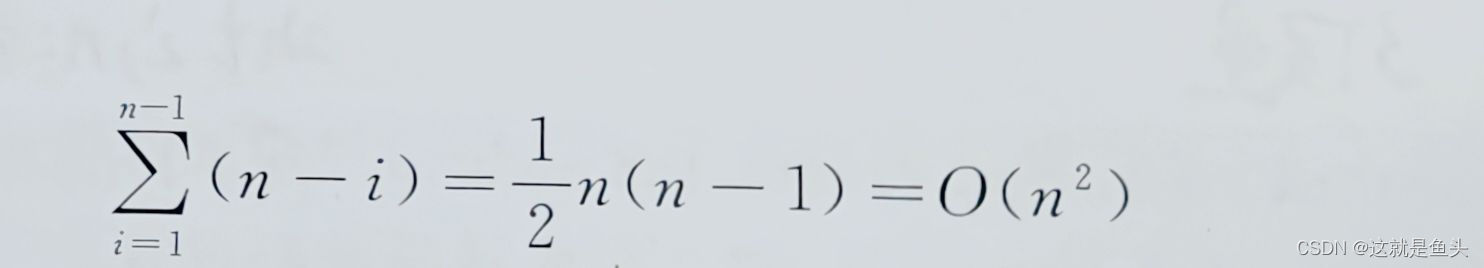
????????平均情況下，設軸值記錄的關鍵碼第k小(1<=k<=n),則有：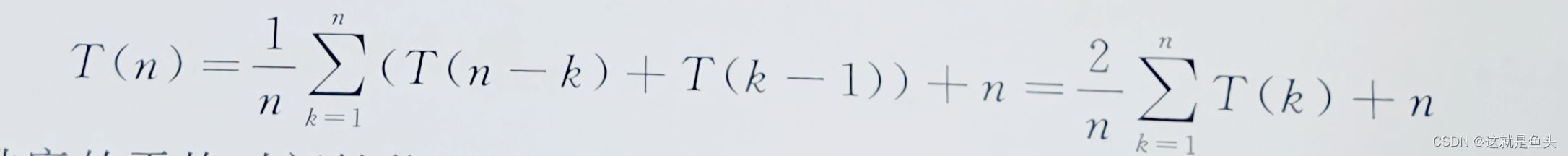

????????這是快速排序的平均時間性能，可以用歸納法證明，其數量級也為O(nlog以2為底n)。
????????由于快速排序是遞歸執行的，需要一個工作棧來存放每一層遞歸調用的必要信息，棧
的最大容量與遞歸調用的深度一致。最好情況下要進行[log以2為底n]次遞歸調用，棧的深度為O(log,n);最壞情況下，要進行n-1次遞歸調用，棧的深度為O(n);平均情況下，棧的深度為O(log以2為底n).

6.3.1??最大子段和問題

應用實例
????????國際期貨市場某種商品在某個月的第1,2，...，31天的價格漲幅分別記為a1,?a2,...,a31,若某天的價格下跌，這天的漲幅就是負值。如果想知道在連續哪些天，該商品的價格具有最高漲幅，究竟漲了多少，這個問題就可以抽象為最大子段和問題。

【算法實現】?最大子段和問題是按照位置進行劃分的，設變量?center?表示序列的中間位置，數組a[n]存放整數序列，程序如下。

#include <iostream>
using namespace std;

int MaxSum(int a[ ], int left, int right)
{
int sum = 0, midSum = 0, leftSum = 0, rightSum = 0;
int i, center, s1, s2, lefts, rights;
if (left == right) //如果序列長度為1，直接求解
sum = a[left];
else
{
center = (left + right)/2; //劃分
leftSum = MaxSum(a, left, center); //對應情況①，遞歸求解
rightSum = MaxSum(a, center+1, right); //對應情況②，遞歸求解
s1 = 0; lefts = 0; //以下對應情況③，先求解s1
for (i = center; i >= left; i--)
{
lefts += a[i];
if (lefts > s1) s1 = lefts;
}
s2 = 0; rights = 0; //再求解s2
for (i = center + 1; i <= right; i++)
{
rights += a[i];
if (rights > s2) s2 = rights;
}
midSum = s1 + s2; //計算情況③的最大子段和
if (midSum < leftSum) sum = leftSum; //合并解，取較大者
else sum = midSum;
if (sum < rightSum) sum = rightSum;
}
return sum;
}
int main( )
{
? int max, n = 6, r[6] = {-20, 11, -4, 13, -5, -2};
? ? max = MaxSum(r, 0, n - 1);
? ? cout << "最大子段和是：" << max << endl;
? ? return 0;

}
?