????????復數移相，也稱為復數相位旋轉，就是在原有復數的基礎上，不改變模數，只把相位角做一定的偏移。

文章目錄

前言

三角函數移相

復數乘法移相

分析和應用

總結

---

前言

??????? 見《【研發日記】Matlab/Simulink技能解鎖(二)——在Function編輯窗口Debug》

????????見《【研發日記】Matlab/Simulink技能解鎖(三)——在Stateflow編輯窗口Debug》

????????見《【研發日記】Matlab/Simulink技能解鎖(四)——在Simulink Debugger窗口調試》

????????見《【研發日記】Matlab/Simulink技能解鎖(五)——七個Simulink布線技巧》

????????見《【研發日記】Matlab/Simulink技能解鎖(六)——六種Simulink模型架構》

?????

三角函數移相

????????三角函數移相法，是利用模數和實部虛部之間的三角函數關系，從原復數求得新復數。在Simulink中建立的移相函數，如下所示：

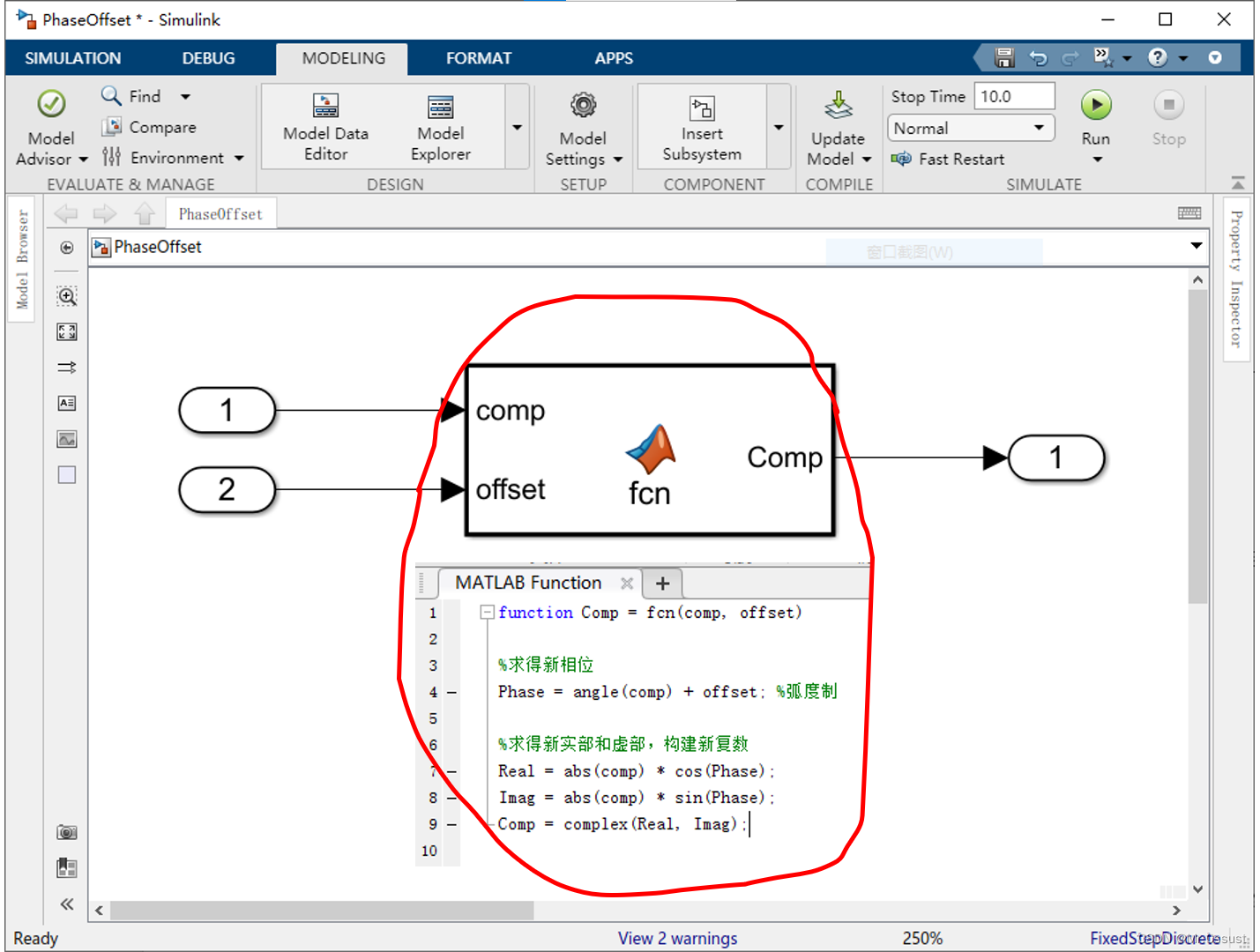
????????Tips： offset的范圍在-π到π之間，輸入接口要做溢出處理。

????????上述模型編譯出來的代碼，如下所示：

#include "PhaseOffset.h"
#include "PhaseOffset_private.h"/* External inputs (root inport signals with default storage) */
ExtU_PhaseOffset_T PhaseOffset_U;/* External outputs (root outports fed by signals with default storage) */
ExtY_PhaseOffset_T PhaseOffset_Y;/* Real-time model */
static RT_MODEL_PhaseOffset_T PhaseOffset_M_;
RT_MODEL_PhaseOffset_T *const PhaseOffset_M = &PhaseOffset_M_;
real_T rt_atan2d_snf(real_T u0, real_T u1)
{real_T y;int32_T u0_0;int32_T u1_0;if (rtIsNaN(u0) || rtIsNaN(u1)) {y = (rtNaN);} else if (rtIsInf(u0) && rtIsInf(u1)) {if (u0 > 0.0) {u0_0 = 1;} else {u0_0 = -1;}if (u1 > 0.0) {u1_0 = 1;} else {u1_0 = -1;}y = atan2(u0_0, u1_0);} else if (u1 == 0.0) {if (u0 > 0.0) {y = RT_PI / 2.0;} else if (u0 < 0.0) {y = -(RT_PI / 2.0);} else {y = 0.0;}} else {y = atan2(u0, u1);}return y;
}/* Model step function */
void PhaseOffset_step(void)
{real_T Out1_tmp;real_T Phase;/* MATLAB Function: '<Root>/MATLAB Function' incorporates:*  Inport: '<Root>/In1'*  Inport: '<Root>/In2'*/Phase = rt_atan2d_snf(0.0, PhaseOffset_U.In1) + PhaseOffset_U.In2;Out1_tmp = fabs(PhaseOffset_U.In1);/* Outport: '<Root>/Out1' incorporates:*  MATLAB Function: '<Root>/MATLAB Function'*/PhaseOffset_Y.Out1.re = Out1_tmp * cos(Phase);PhaseOffset_Y.Out1.im = Out1_tmp * sin(Phase);
}/* Model initialize function */
void PhaseOffset_initialize(void)
{/* Registration code *//* initialize non-finites */rt_InitInfAndNaN(sizeof(real_T));
}/* Model terminate function */
void PhaseOffset_terminate(void)
{/* (no terminate code required) */
}

復數乘法移相

????????當一個復數乘以另一個相位角為θ的復數時，那么前者的相位就會偏移θ。如果后者是單位復數（模數為1），那么前者的模數不變，只跟隨θ旋轉相位角。用這種算法建立的移相函數如下所示：

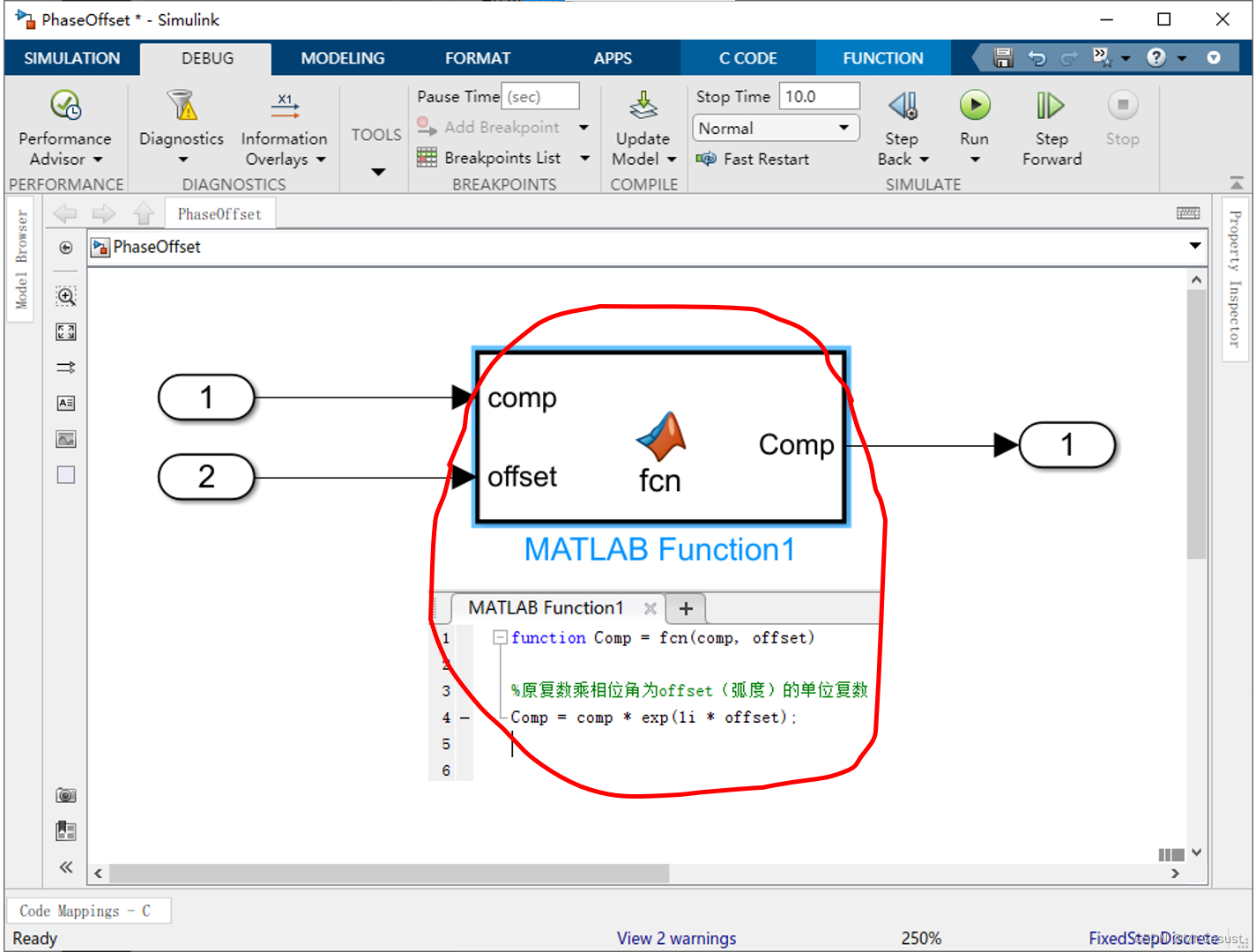
????????Tips：exp(1i * offset) = cos(offset) + sin(offset)i。

????????上述模型編譯出來的代碼，如下所示：

#include "PhaseOffset.h"
#include "PhaseOffset_private.h"/* External inputs (root inport signals with default storage) */
ExtU_PhaseOffset_T PhaseOffset_U;/* External outputs (root outports fed by signals with default storage) */
ExtY_PhaseOffset_T PhaseOffset_Y;/* Real-time model */
static RT_MODEL_PhaseOffset_T PhaseOffset_M_;
RT_MODEL_PhaseOffset_T *const PhaseOffset_M = &PhaseOffset_M_;/* Model step function */
void PhaseOffset_step(void)
{real_T r;real_T y_re;/* MATLAB Function: '<Root>/MATLAB Function1' incorporates:*  Inport: '<Root>/In2'*/if (PhaseOffset_U.In2 == 0.0) {y_re = exp(PhaseOffset_U.In2 * 0.0);r = 0.0;} else {r = exp(PhaseOffset_U.In2 * 0.0 / 2.0);y_re = r * cos(PhaseOffset_U.In2) * r;r *= r * sin(PhaseOffset_U.In2);}/* Outport: '<Root>/Out1' incorporates:*  Inport: '<Root>/In1'*  MATLAB Function: '<Root>/MATLAB Function1'*/PhaseOffset_Y.Out1.re = PhaseOffset_U.In1 * y_re;PhaseOffset_Y.Out1.im = PhaseOffset_U.In1 * r;
}/* Model initialize function */
void PhaseOffset_initialize(void)
{/* (no initialization code required) */
}/* Model terminate function */
void PhaseOffset_terminate(void)
{/* (no terminate code required) */
}

分析和應用

????????復數移相在嵌入式軟件開發中應用非常廣泛，尤其是在電源設計和電機控制領域。上述兩種移相算法都能實現相同的功能，但是具體運算過程略有差別，可以從兩者的C代碼中進行分辨。

????????三角函數移相主要用到的運算是arctan()、abs()、cos()、sin()等，復數乘法移相主要用到的運算是e^()、cos()、sin()等，其中的abs()實質是平方和開方，e^()也是n次方，所以底層運算基本上都是一樣的。

????????在matlab函數中，復數乘法移相的運算步驟更加精簡。在底層C代碼中，三角函數移相的運算步驟更加精簡。

????????綜上，可以根據自己的開發理念選取合適的移相算法。如果注重運行高效，就選擇三角函數移相。如果注重開發代碼精煉的，就選擇復數乘法移相。

總結

????????以上就是本人在研發中使用Simulink開發復數移相算法時，一些個人理解和分析的總結，主要介紹了兩種移相算法的工作原理，展示了算法運行的效果，并分析了這兩種算法的特點和適用場景。

????????后續還會分享另外幾個最近解鎖的Matlab/Simulink新技能，歡迎評論區留言、點贊、收藏和關注，這些鼓勵和支持都將成文本人持續分享的動力。

????????另外，上述例程使用的Demo工程，可以到筆者的主頁查找和下載。

---

????????版權聲明，原創文章，轉載和引用請注明出處和鏈接，侵權必究！