墨色規則與血色節點：C++紅黑樹設計與實現探秘

前言

??? ?前幾天攻克了AVL樹，我們已然是平衡二叉樹的強者。但旅程還未結束，下一個等待我們的，是更強大、也更傳奇的**終極BOSS**——紅黑樹。它不僅是map和set的強大心臟，更是C++ STL皇冠上的明珠。準備好了嗎？讓我們一起揭開它的神秘面紗。

1.紅黑樹的概念

1.1.紅黑樹是什么

??? ?紅黑樹是一科二叉搜索樹，他的每個節點增加一個存儲為代表著該節點的顏色，和它的名字一樣，節點的顏色可以是紅色或者是黑色。通過對任何一條根到葉子的路徑上各個節點的顏色進行約束，紅黑樹確保沒有一條路徑會比其他路徑長出2倍，因而是接近平衡的。

??? ?紅黑樹是被很多條規則進行束縛的二叉搜索樹，通過這些規則，可以保證紅黑樹沒有一條路徑會比其他路徑長出2倍，并且保持其相對平衡，下面我來講述一下這些規則。

1.2.紅黑樹的規則

??? ?1.每個節點不是黑色的就是紅色的（這肯定，不然不會被叫做紅黑樹了）。

??? ?2.根節點必須是黑色的

??? ?3.如果一個節點是紅色的，則它的兩個孩子節點必須是黑色的，也就是說任意一條路徑上并不會出現連續的紅色的節點。

??? ?4.對于任意的一個節點，從該節點到其所有的NULL節點的簡單路徑上，均包含著相同數目的黑色節點。

??? ?以上便就是紅黑樹的四條規則，其實《算法導論》上也是補充了一個知識點：每個葉子節點（NULL）都是黑色的規則。他這里所指的葉子節點不是傳統意義上的葉子節點，而是我們所說的空節點，有些書籍上也把NULL叫做外部節點。NULL是為了方便準確的標志處所有路徑，《算法導論》在后續實現的細節中忽略了NULL節點，所以我們知道這個概念即可。下面我放幾張紅黑樹的示意圖。

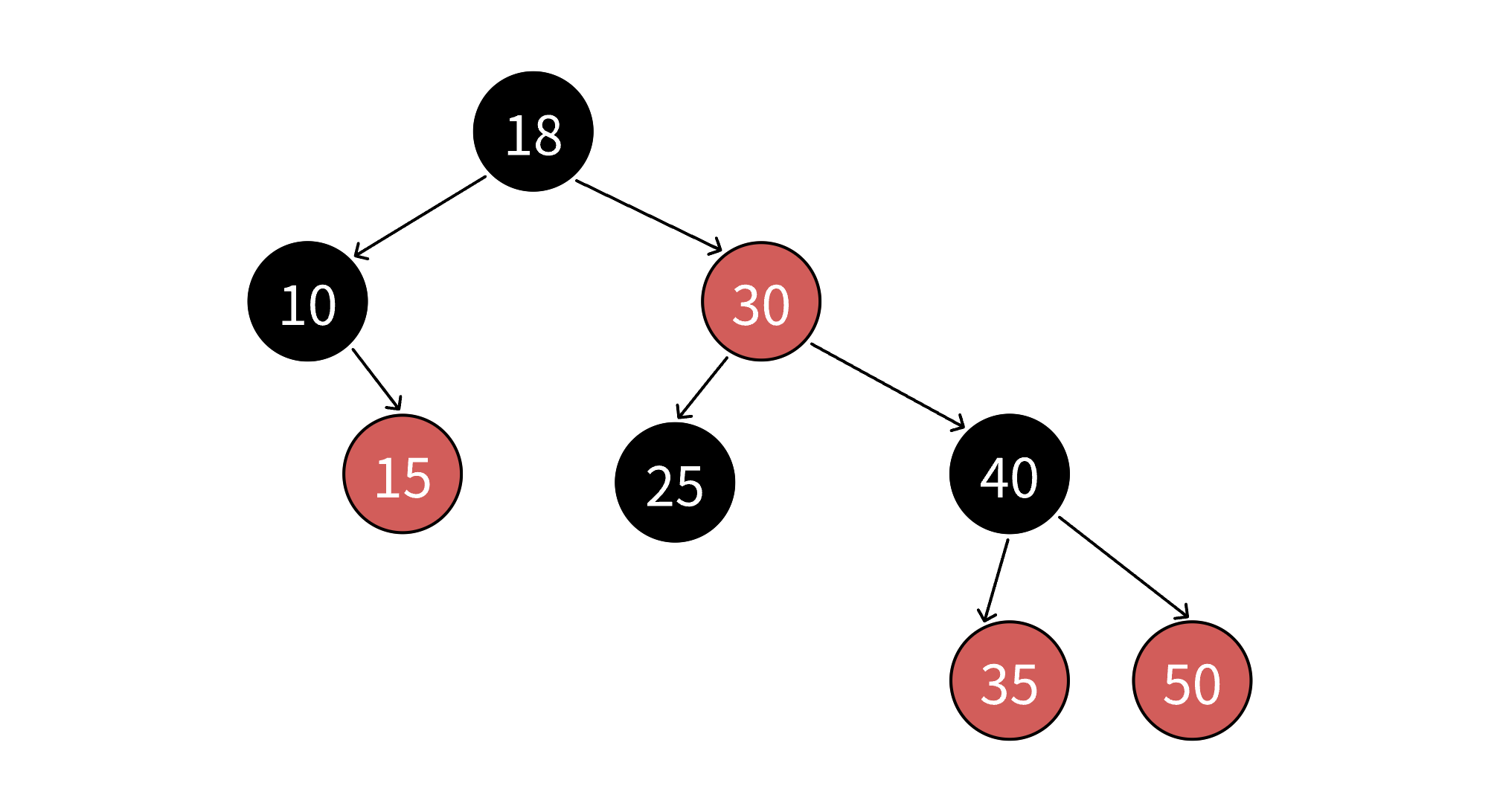
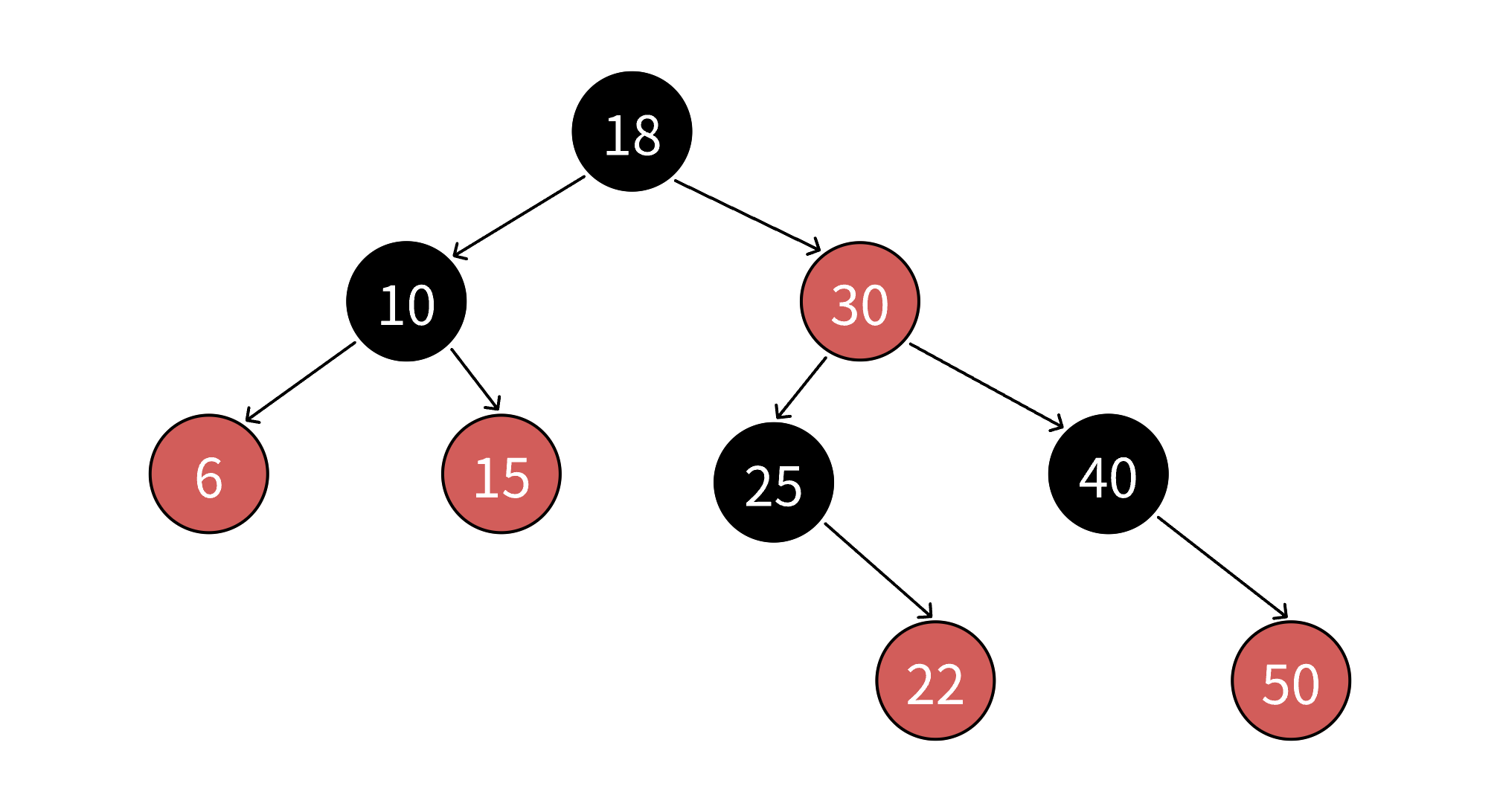
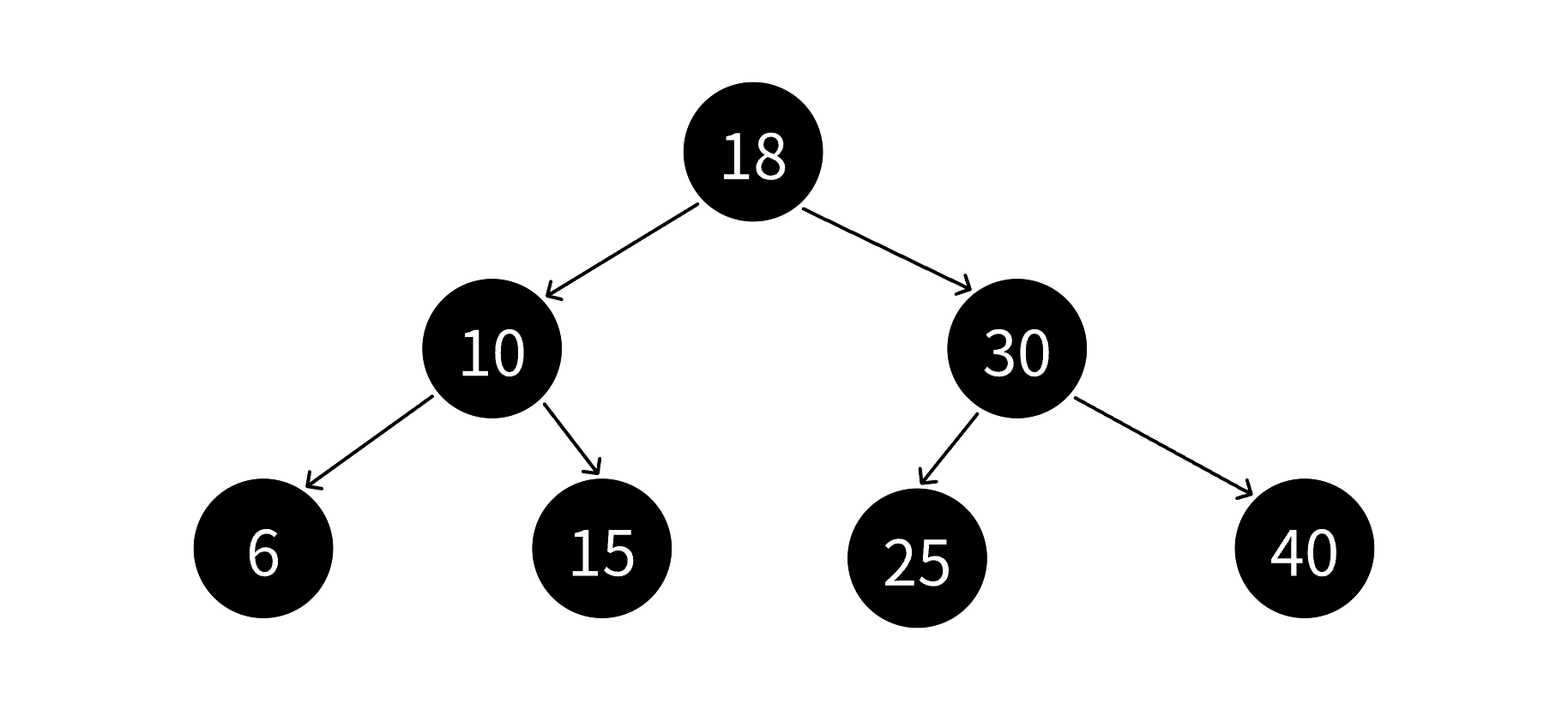
1.3.紅黑樹如何確保最長路徑不超過最短路徑的兩倍

??? ?由規則4可以知道，每條路徑上有著數量相同的黑色節點，所以在極端場景下，就比如上面最后一個圖，一條路上全都是黑色節點，最短路徑其實就是一條路上全是黑色節點，我們將最短路徑的長度記作bh。

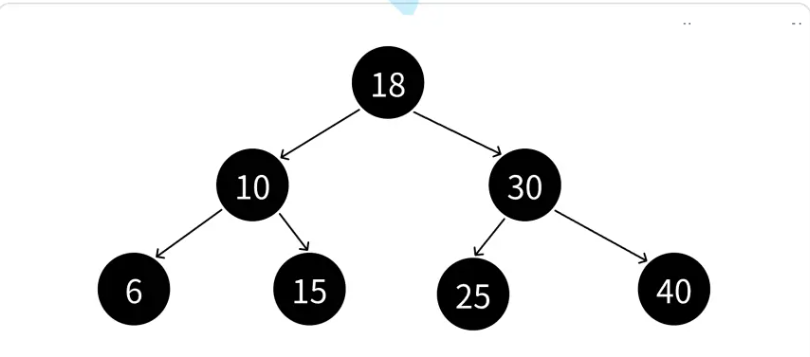
??? ?在看規則2和規則三，我們可以清楚的知道，一條路上不會出現連續的紅色節點，所以我們容易知道最長路徑應該是一紅一黑交織組成，所以最長路徑的長度是2bh。

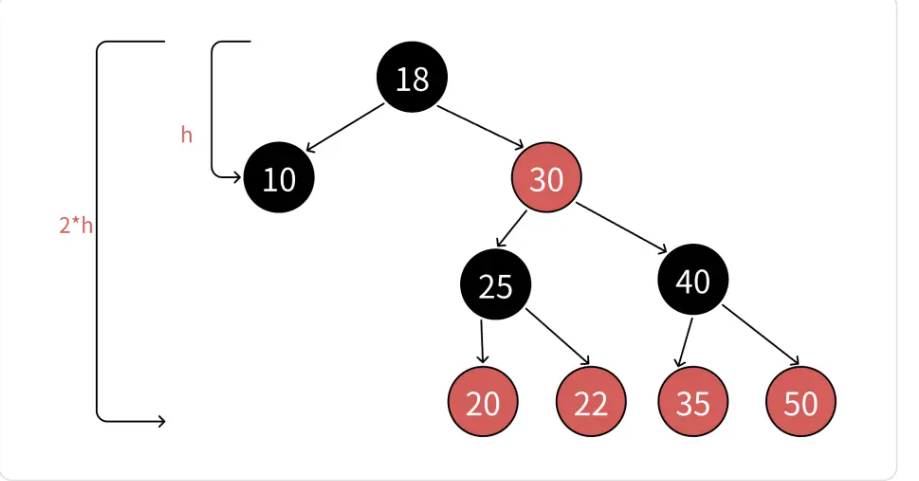
??? ?根據紅黑樹的規則，我們可以知道一般情況下的紅黑樹的路徑是由數量不等的紅黑節點組成的，一紅一黑交織進行和全是黑的是不太容易出現的，所以假設紅黑樹一條路徑的長度為h，所以bh<=h<=2bh，即紅黑樹的最長路徑不會是最短路徑的兩倍。

1.4.紅黑樹的效率問題

??? ?我們假設紅黑樹的節點個數為N，最短路徑的長度為h，所以可知：2^h - 1 <= N < 2^2*h - 1，由此可以推出h大約等于logN，也就是紅黑樹搜查的效率問題最差也是2 * logN，時間復雜度終歸還是O（log（N））。

??? ?紅黑樹的表達相對AVL樹是要更抽象一些的，AVL樹可以根據高度更加直觀的看出樹的平衡，而紅黑樹則是需要根據四條規則的顏色進行約束，間接的實習了近似平衡，他們的效率都是同一檔次的，但是相對而言，插入相同數量的節點，紅黑樹的旋轉次數變的更少了，因為它對平衡的把控并不是那么的嚴格。

2.紅黑樹的實現

2.1.紅黑樹的結構

??? ?在我們書寫平衡樹的代碼之前，通常我們需要先完善一下它的結構，就比如其中最基礎的，它的每個節點應該存儲什么的數據，紅黑樹也是一個典型的三叉鏈，所以它的節點需要包含它的父節點以及左右孩子節點，并且由于紅黑樹是通過顏色進行平衡的位置，我們還需要設置好一個聯合體來確定節點的顏色，我們默認顏色就是紅色，并且紅黑樹也是通過Key和Value進行存放數據的，Key就好比我們開車進入商場停車場的車牌號，而Value就是記錄進入停車場的時間的，由此來確定需要繳納多少錢。所以由此來看Key就是一個標記，而紅黑樹真正的核心應該是Value。下面我來展示一下紅黑樹結構相關的代碼。

enum Colour
{RED,BLACK
};
// 這里我們默認按key/value結構實現
template<class K, class V>
struct RBTreeNode  //struct不用域作用限定符默認就是
{// 這里更新控制平衡也要加入parent指針pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;  //存放節點的顏色RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr),_col(RED){}
};
template<class K,class V>
class RBTree
{typedef RBTreeNode<K,V> Node;
public:
private:Node* _root = nullptr;
}

2.2.紅黑樹的查找

??? ?紅黑樹的查找和二叉搜索樹的查找是一樣的，代碼也是比較類似的，它們的效率都是log(N)，所以我就不在細講了，看不懂的讀者可以加我主頁的微信詢問我。

Node* Find(const K& key)
{Node* cur = _root; //代替根節點去便利while (cur){if (cur->_kv.first > key){cur = cur->_left;}else if (cur->_kv.first < key){cur = cur->_right;}else{return cur;}}return NULL;
}

3.紅黑樹的插入

??? ?下面我們就進入到了紅黑樹最難的部分（刪除不算）：紅黑樹的插入，紅黑樹的插入的復雜程度還是和AVL數比較類似的，但是我個人感覺紅黑樹相對AVL樹更加抽象一些，因為它不僅僅涉及到了旋轉，還有變色的操作，依次來維持它的那四條規則，廢話不多說，接下來我們進入紅黑樹的插入講解。

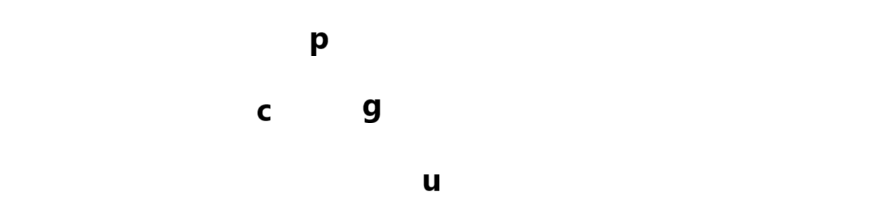
??? ?在講插入過程的時候事先說明一下：假設我們把新增的節點叫做c(cur)，c的父親則標記為p（parent），p的父親節點標記為g（grandfather），p的兄弟節點表姐為u（uncle）。

3.1.紅黑樹插入一個值的大致過程

??? ?插入一個值是按照二叉搜索樹的規則來進行的，插入后的值我們需要讓其符合紅黑樹的四條規則。如果是空樹插入，那么插入的必然就是黑色節點，因為根節點必須是黑色的；如果是非空樹插入，那么插入的節點一定是紅色的，因為第四條規則約束著，如果插入的是黑色節點，那么第四條規則就被破壞了。非空樹在插入的時候，插入的節點必須是紅色節點，如果其父節點是黑色的，那么并沒有違法規則，插入成功。如果其父節點是紅色的，那么就違反了第三條規則。進一步的分析，c是紅色，p也是紅色，那么g必然是黑色的（如果g也是紅色的那么就說明在沒有插入c的時候此樹已經違反規則了），這三個的顏色都已經定了，所以關鍵的變化還得看u的變化，分別需要分為以下四種情況討論，在討論之前，我先把插入的相關代碼放到下面（和二叉搜索樹差不多）。

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;  //根節點一定是黑色的}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{//cout << "重復節點不可插入" << endl;  //數據少可以這么寫，數據多，就會很難受，循環多次才結束return false;}}//走到這說明插入成功了cur = new Node(kv);cur->_col = RED; //新插入的結點一定是紅色//開始進行變色處理//和父親結點進行配對if (parent->_kv.first < kv.first){//比父親結點大，插在右邊parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;  //這個一定不可以忘掉
}

3.2.情況一：變色

1.講解

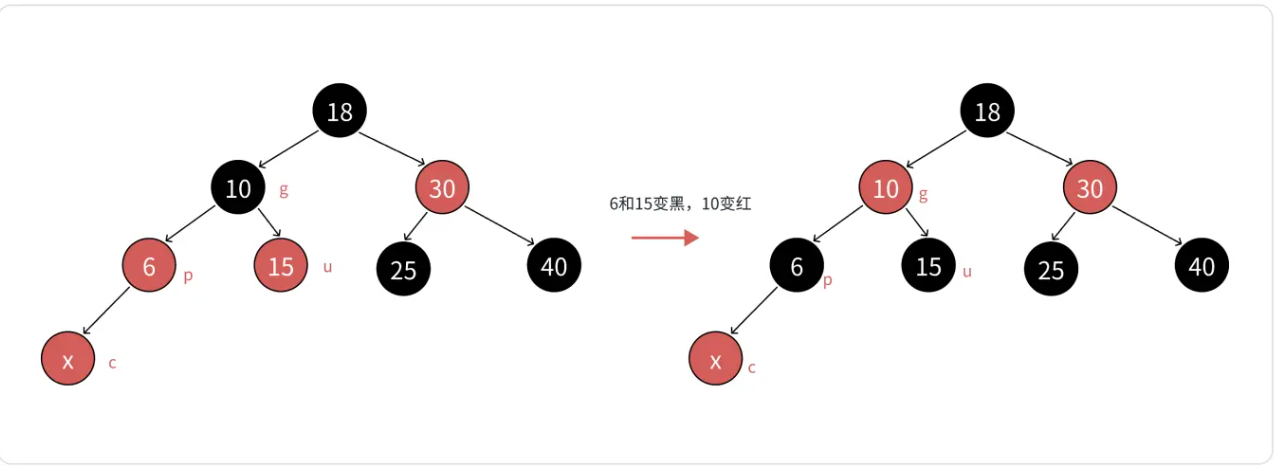
??? ?如上圖所示，如果c是紅的，p為紅，g為黑，u存在并且是紅色的話，那么我們就需要進行變色處理，即將p和u都變為黑色，g變紅。再把g當做新的c，繼續往上進行更新。可能很多讀者不曉得我這么做的原因，下面我將進行解釋。

??? ?因為p和u均是紅色，g是黑色，把p和u都變為黑色，左右子樹都多增加了一個黑色節點，g變為了紅色，因為著p和u所在的支路上黑色節點的個數是沒有變化的，這樣就沒有違反規則四，并且同時解決了紅色節點的孩子還是紅色節點的問題；至于為何讓g變為新的c，因為g的父節點我們并不知曉是什么顏色的，倘若還是黑色，那就皆大歡喜，不用在往上進行遍歷了；但是如果是紅色，那么我們還需進行變色處理。不過還有一種情況，就是g就是整棵樹的根，那么我們就需要把g變為黑色，因為紅黑樹的根節點是黑色的。

??? ?當然，上圖是屬于第一種變色的特殊情況，和AVL樹類似，我們還需了解抽象狀態下的AVL樹的變色，如下圖所示。

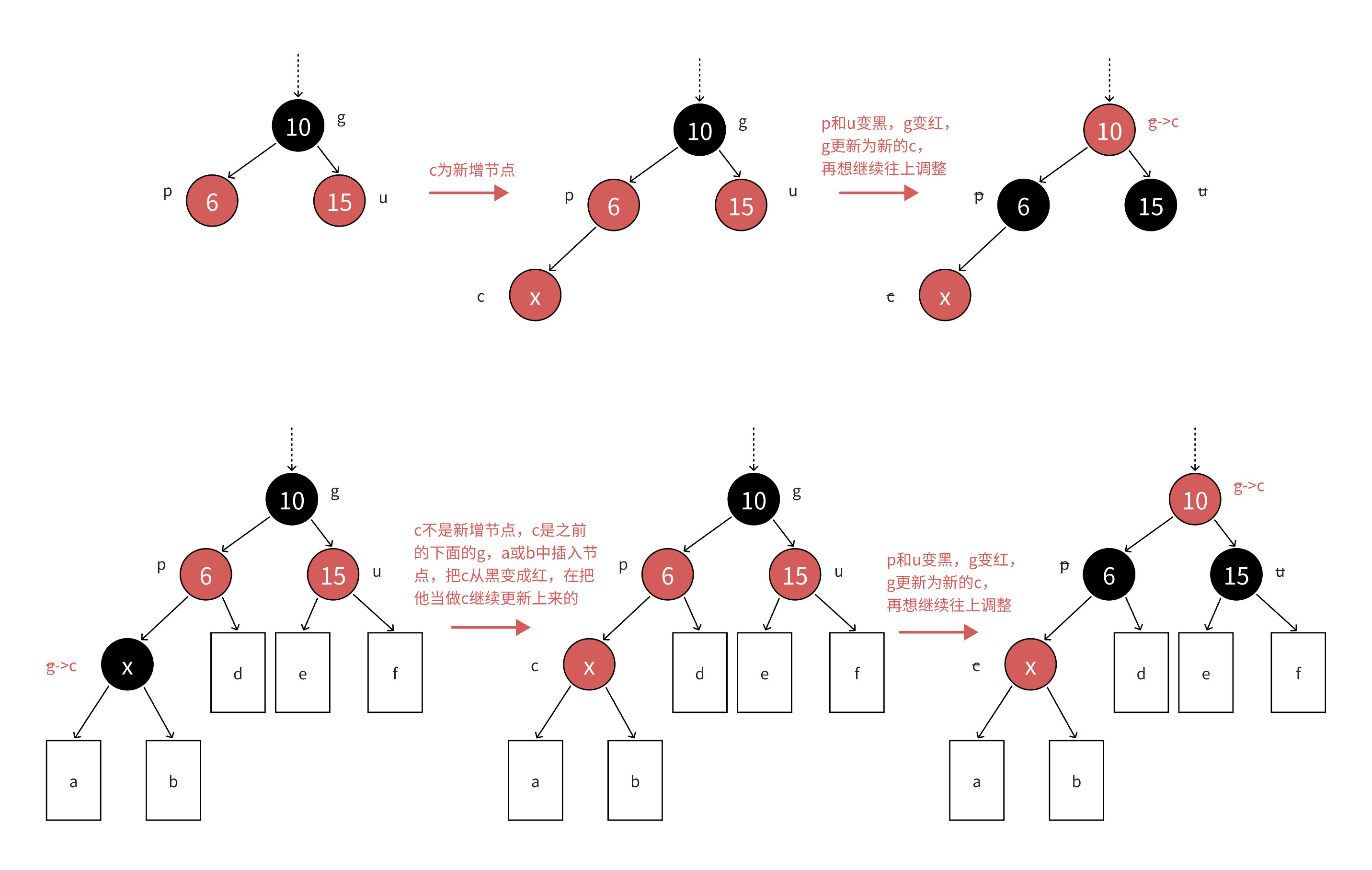
??? ?上圖則是對變色進行了比較抽象的表達，d，e，f代表著每條路徑上有hb個黑色節點的子樹，a/b則代表著每條路徑上擁有hb-1個黑色節點的根為紅的子樹，其中hb>=0，下面這個情況就形象的代表了當我們在a或者b中進行了一次變色，傳遞到上面時，可能也會讓上面進行變色處理。當然不，情況一僅僅設計了變色的處理，而不涉及旋轉，所以左右子樹都是相同的變色處理，以上就是情況一的講解，下面我們進入代碼的講解。

2.代碼

??? ?此時我們還需要劃分此時的父親節點是左子樹還是右子樹，下面我們就單拿左子樹為例，因為左右子樹都是差不多的，掌握了一種，另一種也是會更為輕松的掌握。

??? ?剛開始，我們需要先把g節點表示出來，即p節點的父親節點，因為我們進行變色處理以后，需要往上進行更新，所以變色的操作應該是一次次循環的過程。

while (parent && parent->_col == RED)
{Node* grandfather = parent->_parent;
}

??? ?我們需要通過if語句確認p節點是在左邊的，之后我們需要把u節點表示出來，如果此時u節點存在并且u節點就是紅色的，那么就符合情況一，之后我們先把p和u節點都染成黑色的，再把g節點變為紅色的，做完這些操作以后，我們就需要更新一下c和p節點了更新結束，代表一次變色成功，繼續往上進行更新。

if (grandfather->_left == parent)
{Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){//單純的變色處理grandfather->_col = RED;parent->_col = BLACK;uncle->_col = BLACK;//在往上進行查詢cur = grandfather;parent = cur->_parent;}
}
1.完整變色（p節點在左邊）
while (parent && parent->_col == RED)
{Node* grandfather = parent->_parent;//先來節點都是左邊的情況if (grandfather->_left == parent){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){//單純的變色處理grandfather->_col = RED;parent->_col = BLACK;uncle->_col = BLACK;//在往上進行查詢cur = grandfather;parent = cur->_parent;}}
}
2.完整變色（p節點在右邊）
if(grandparent->_right == parent)
{Node* uncle = grandfather->_left;if (uncle&& uncle->_col == RED){grandfather->_col = RED;parent->_col = BLACK;uncle->_col = BLACK;//在往上進行查詢節點是否正確cur = grandfather;parent = cur->_parent;}
}

3.3.情況二：單旋+變色

1.講解

??? ?又看到了我們的老朋友：單旋了，上次我們和它見面還是AVL樹，沒想到到了紅黑樹，它又來追殺我們了（┭┮﹏┭┮），不過紅黑樹的單旋其實和AVL樹是類似的，這意味著我們可以直接使用AVL樹的單旋代碼（(#^.^#)），下面我通過一個特殊的例子來給各位講解情況二。

??? ?如果c是紅色，p是紅色，g為黑，u不存在或者u是黑色的時候，這個時候我們就不能單單依靠表變色進行紅黑樹的修正了，因為這樣會違反規則四；如果u不存在，那么c一定就是新的節點；如果u是黑的，那么c一定不是新的節點，而是因為之前c本來就是黑色的節點，但是由于進行了變色處理，導致c變成了紅色節點。

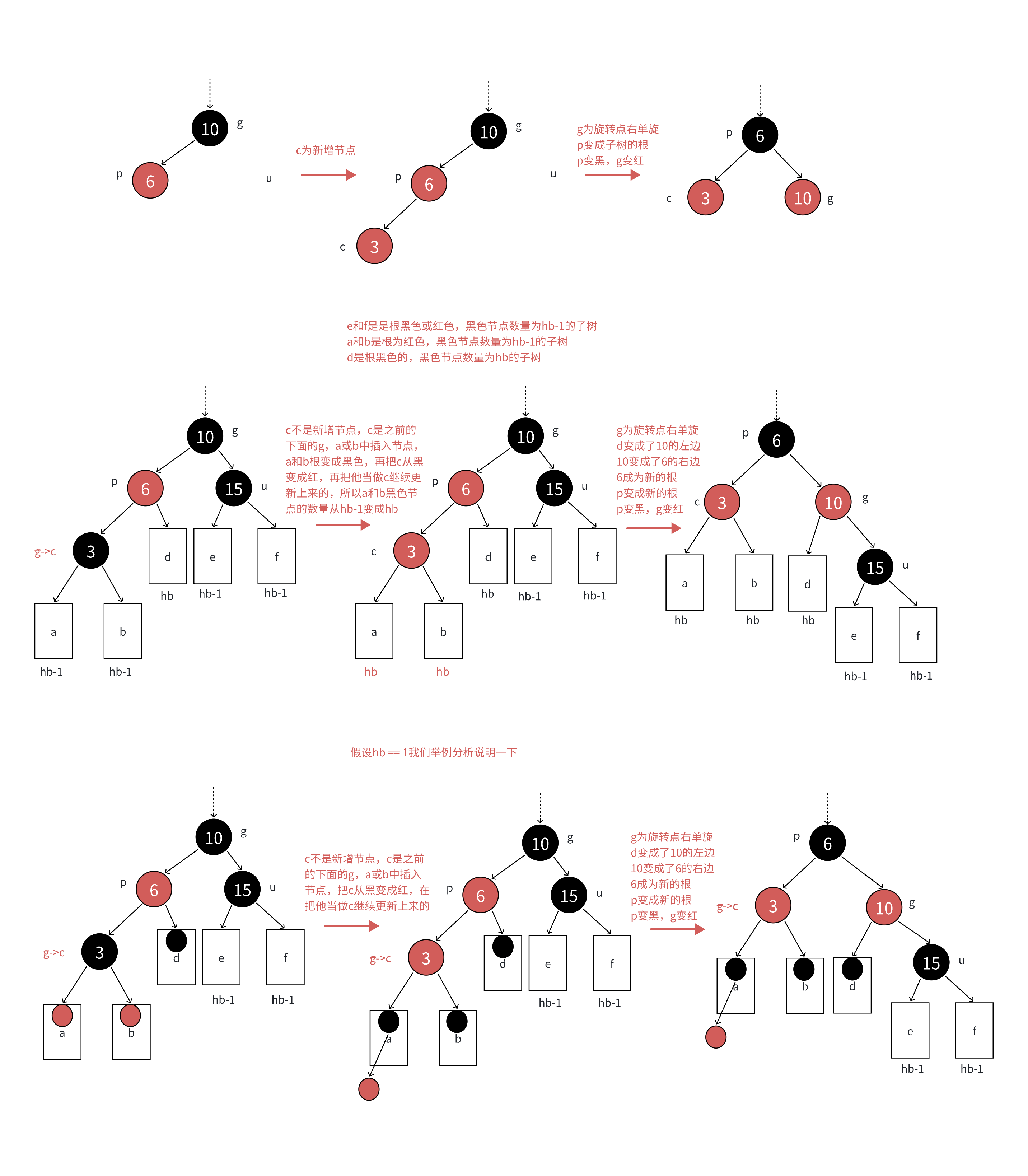
??? ?如果p是g的左子樹，如上圖所示，c是p的左子樹，那么我們就以g為旋轉點，先進行一次右單旋，如下圖所示。

??? ?此時我們需要讓g變為紅色，p變為黑色即可。此時p變成了這棵子樹新的根了，這樣子樹黑色節點的數量不變，沒有連續的紅色節點，并且還不需要往上進行更新了，因為p的父親無論是啥都沒會違反這些規則了。

??? ?如果p是g的右子樹，c是p的右，如上圖所示，那么我們還是以g為旋轉點，但是是左單旋，如下圖所示。

??? ?此時我們需要讓p變為黑色，g變為紅色即可，p變為了新子樹的根，這樣子樹的黑色節點的數量并沒有改變，沒有連續的紅色節點，并且還不需要往上進行更新了。

??? ?當然，我們學完了特殊情況，還需要知曉一些抽象情況，下面我就放上一張圖片，希望各位讀者自行閱讀。

2.代碼

??? ?首先我們需要先知曉，此時的情況二也是在循環之中的，此時我們還是以右單旋為例進行講解，當c為p的左孩子時，意味著此時我們需要單旋進行處理（前提是u節點為黑色或者是空），那么此時我們需要進行單旋處理，單旋的話我們直接把AVL樹的單旋copy過來即可（忘了的看我上一篇文章），之后在進行相應的變色處理即可。下面我把兩個完整代碼展示出來。

1.右單旋+變色
if(uncle -> col == black || uncle == nullptr)
{if(parent -> left == cur){//右單旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;break;  //無須在往上走了}
}
2.左單旋+變色
if(uncle -> col == black || uncle == nullptr)
{if(parent -> right == cur){//進行左單旋處理RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}
}

3.情況三：雙旋+變色

??? ?既然都有單旋這種情況了，那么雙旋也是必不可少的，當然，雙旋的代碼還是和AVL樹是一樣的（(#^.^#)），減少了很大部分的工作量。

1.講解

??? ?情況三的顏色情況其實和情況二是類似的，它們均是c和p都是紅色，g為黑色，u是不存在或者為黑色，所以下面我們進入雙旋情況的講解。

??? ?如果p是g的左，c是p的右，此時我們僅僅依靠單旋是不可以進行紅黑樹的糾正的，所以此時我們就需要通過雙旋進行調整，我們先以p為旋轉點進行一次左旋，在以g進行一次右旋，如下圖所示。

??? ?此時我們僅需讓c變為黑色，g變為紅色即可，c變成了這棵樹新的根，這樣做黑色節點的數目沒有改變，沒有連續的紅色節點了，因為g是黑色，此時無論他的父節點是什么，都不會影響結果了。

??? ?如果此時p是g的有孩子，c是p的左孩子，這個時候我們也是需要雙旋進行處理的，先以p為旋轉點進行右旋，再以g為旋轉點進行左旋，之后把c變為黑色，g為紅色即可。

??? ?以上是紅黑樹情況二的特殊情況，下面我們來看看一般情況，即抽象表達，看一看下圖的圖，我相信你會懂的。

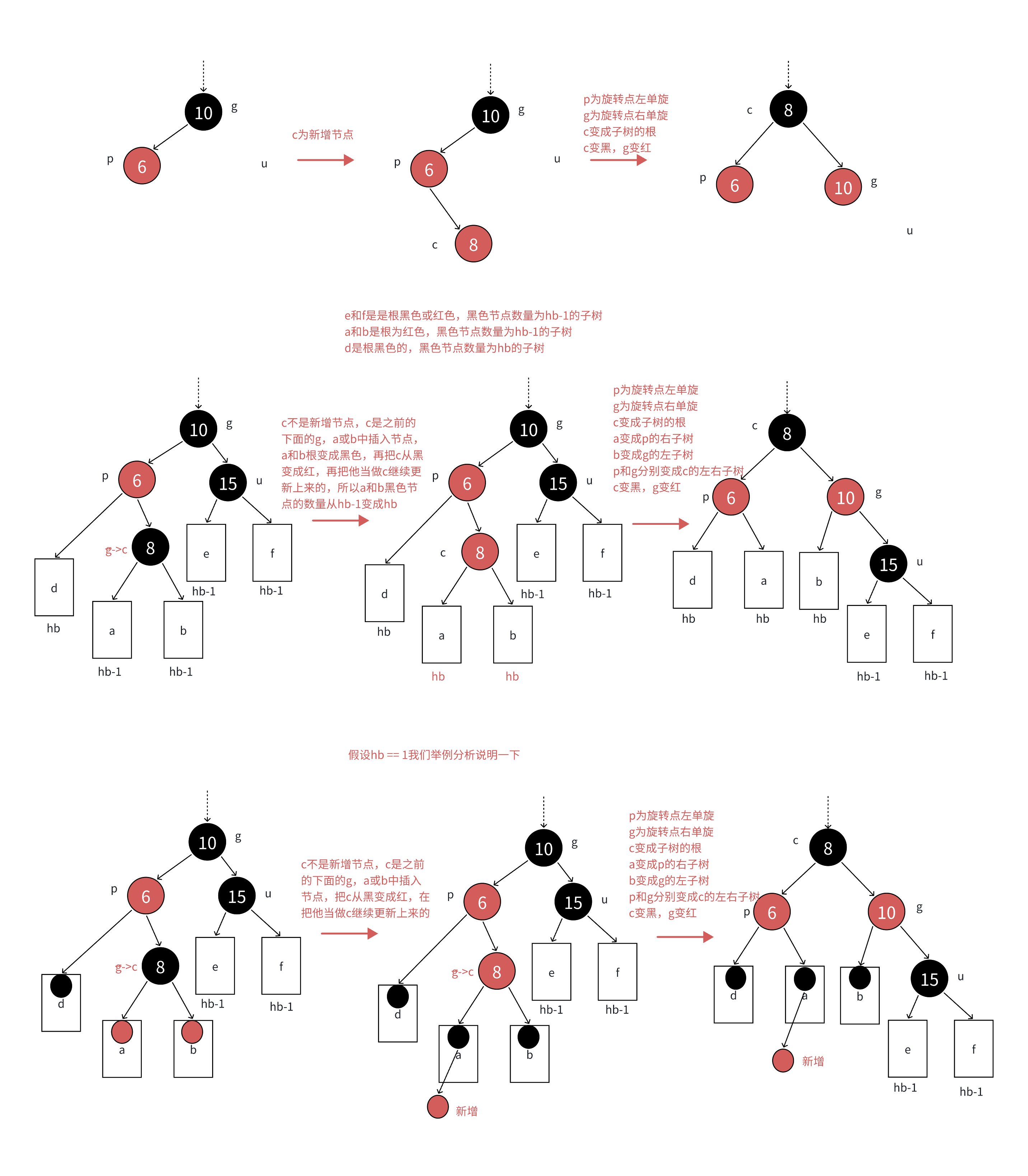
2.代碼

??? ?我個人認為情況三的代碼比較容易，各位讀者通過我上面的講解應該就知曉代碼如何書寫了，所以我下面直接放代碼（不會的讀者可以私信詢問我）。

如果p是g的左孩子
//左右雙旋轉
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
如果p是g的右孩子
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;

4.紅黑樹的驗證

1.如何驗證

??? ?此時我們已經講述完了紅黑樹相關知識點的講解，可能有很多讀者想知道自己寫的紅黑樹是否是正確的，下面我將給各位講述一下如何驗證自己寫的紅黑樹。此時我們需要檢驗四條規則，如果滿足這四條規則，那么說明這棵樹就是一顆非常棒的紅黑樹。

??? ?1.規則一枚舉顏色類型，天然的實現保證了節點非紅即黑。

??? ?2.規則二直接檢查根部即可

??? ?3.規則三進行前序遍歷檢查，遇到紅色節點檢查孩子不太方便，因為孩子是有兩個的，并且不一定就是存在的，反過來檢查顏色就方便多了。

??? ?4.規則四進行前序遍歷，遍歷過程中用形參記錄根到當前節點的黑色節點的數量，前序遍歷遇到黑色節點就++blackNum，走到空就計算一條路徑黑色節點的數量。以任意一條路徑的黑色節點數量作為基準，依次比較即可。

2.相關代碼

bool Check(Node* root, int blackNum, const int refNum)
{if (root == nullptr){// 前序遍歷走到空時，意味著一條路徑走完了//cout << blackNum << endl;if (refNum != blackNum){cout << "存在黑色結點的數量不相等的路徑" << endl;return false;}return true;}// 檢查孩子不太方便，因為孩子有兩個，且不一定存在，反過來檢查父親就方便多了if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在連續的紅色結點" << endl;return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);
}

5.紅黑樹的刪除

??? ?和AVL樹一樣，由于我現在并沒有掌握紅黑樹的刪除，所以各位讀者如果想要理解可以看一下其他博主的博文，小編目前還不會這個，希望我以后會掌握。

6.完整代碼

#pragma once
#include<iostream>
#include<vector>
#include<assert.h>
#include<ctime>
//這里將要進行紅黑樹的實現namespace wang
{using namespace std;//先設置好相應的顏色以及結點的相關屬性（這里我就直接拷貝了）enum Colour{RED,BLACK};// 這里我們默認按key/value結構實現template<class K, class V>struct RBTreeNode  //struct不用域作用限定符默認就是{// 這里更新控制平衡也要加入parent指針pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;  //存放節點的顏色RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr),_col(RED){}};template<class K, class V>class RBTree{typedef RBTreeNode<K, V> Node;private:void RotateR(Node* parent){//進行旋轉處理Node* subl = parent->_left;  //將來要成為父親的Node* sublR = subl->_right;parent->_left = sublR;if (sublR){//如果這個結點存在的話，讓它的父親結點成為parentsublR->_parent = parent;}//此時需要先把P的父親結點保存起來Node* ppnode = parent->_parent;subl->_right = parent;parent->_parent = subl;if (ppnode == nullptr){_root = subl; //證明剛才要調整的parent就是根節點subl->_parent = ppnode;}else{if (subl->_kv.first > ppnode->_kv.first){ppnode->_right = subl;}else{ppnode->_left = subl;}subl->_parent = ppnode;}}void RotateL(Node* parent){//左單旋處理Node* subL = parent->_right;Node* subLL = subL->_left;Node* ppnode = parent->_parent;parent->_right = subLL;if (subLL){subLL->_parent = parent;}//開啟最復雜的一集subL->_left = parent;parent->_parent = subL;if (ppnode == nullptr){_root = subL;subL->_parent = nullptr;}else{if (subL->_kv.first > ppnode->_kv.first){ppnode->_right = subL;}else{ppnode->_left = subL;}subL->_parent = ppnode;   //這個忘加了，想事要想全，這點我確實是大意了}}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}public://插入pair類型的結點bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;  //根節點一定是黑色的}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{//cout << "重復節點不可插入" << endl;  //數據少可以這么寫，數據多，就會很難受，循環多次才結束return false;}}//走到這說明插入成功了cur = new Node(kv);cur->_col = RED; //新插入的結點一定是紅色//開始進行變色處理//和父親結點進行配對if (parent->_kv.first < kv.first){//比父親結點大，插在右邊parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;  //這個一定不可以忘掉while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//先來節點都是左邊的情況if (grandfather->_left == parent){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){//單純的變色處理grandfather->_col = RED;parent->_col = BLACK;uncle->_col = BLACK;//在往上進行查詢cur = grandfather;parent = cur->_parent;}//uncle不存在或者存在且為黑色else{if (parent->_left == cur){//右單旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//左右雙旋轉RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}//旋轉之后肯定就是一個很好的紅黑樹了}//如果是父親結點是右子樹else{Node* uncle = grandfather->_left;if (uncle&& uncle->_col == RED){grandfather->_col = RED;parent->_col = BLACK;uncle->_col = BLACK;//在往上進行查詢節點是否正確cur = grandfather;parent = cur->_parent;}//叔叔節點要不是黑的要不就是空的else{if (parent->_right == cur){//進行左單旋處理RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//先雙旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}//根節點一定是黑色的//_root->_col = BLACK;}_root->_col = BLACK;return true;  //此時說明插入成功}Node* Find(const K& key){Node* cur = _root; //代替根節點去便利while (cur){if (cur->_kv.first > key){cur = cur->_left;}else if (cur->_kv.first < key){cur = cur->_right;}else{return cur;}}return NULL;}void InOrder(){_InOrder(_root); //復用一下就好了，遍歷需要root，平常root對象是穿不了的，所以放在一個函數里面，復用一下}bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){// 前序遍歷走到空時，意味著一條路徑走完了//cout << blackNum << endl;if (refNum != blackNum){cout << "存在黑色結點的數量不相等的路徑" << endl;return false;}return true;}// 檢查孩子不太方便，因為孩子有兩個，且不一定存在，反過來檢查父親就方便多了if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在連續的紅色結點" << endl;return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);}bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED)return false;// 參考值int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);}int Height(){return _Height(_root);}int Size(){return _Size(_root);}protected:int _Size(Node* root){if (root == nullptr)return 0;return _Size(root->_left) + _Size(root->_right) + 1;}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}private:Node* _root = nullptr;};void TestRBTree1(){RBTree<int, int> t;// 常規的測試用例//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };// 特殊的帶有雙旋場景的測試用例int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : a){/*if (e == 14){int x = 0;}*/t.Insert({ e, e });//cout << "Insert:" << e << "->";//cout << t.IsBalanceTree() << endl;}t.InOrder();cout << t.IsBalance() << endl;}void TestRBTree2(){const int N = 1000000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand() + i);}size_t begin2 = clock();RBTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}size_t end2 = clock();cout << t.IsBalance() << endl;cout << "RBTree Insert:" << end2 - begin2 << endl;cout << "RBTree Height:" << t.Height() << endl;cout << "RBTree Size:" << t.Size() << endl;size_t begin1 = clock();// 確定在的值/*for (auto e : v){t.Find(e);}*/// 隨機值for (size_t i = 0; i < N; i++){t.Find((rand() + i));}size_t end1 = clock();cout << "RBTree Find:" << end1 - begin1 << endl << endl;}}

7.小結

??? ?本篇文章到這里也就結束了，這篇文章如果我沒記錯我前前后后大約一周才寫完的，因為我好久沒用C++了，導致我忘記了紅黑樹的相關知識點，所以我其實算是邊學習邊寫博客，所以文章可能會有錯誤，希望讀者不要狠狠的噴小編，小編目前就是個fw，希望我會逐漸掌握自己已經遺忘的知識點，如果文章有錯誤可以在評論區指出，我一定會認真更改的，一起學習的時光總是短暫的，那么各位大佬們，我們下一篇文章見啦！

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/bicheng/98131.shtml
繁體地址，請注明出處：http://hk.pswp.cn/bicheng/98131.shtml
英文地址，請注明出處：http://en.pswp.cn/bicheng/98131.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

大數據時代時序數據庫選型指南：為何 Apache IoTDB 成優選（含實操步驟）

大數據時代時序數據庫選型指南：為何 Apache IoTDB 成優選（含實操步驟）

在數字經濟加速滲透的今天&#xff0c;工業物聯網&#xff08;IIoT&#xff09;、智慧能源、金融交易、城市運維等領域每天產生海量 “帶時間戳” 的數據 —— 從工業設備的實時溫度、電壓&#xff0c;到電網的負荷波動&#xff0c;再到金融市場的每秒行情&#xff0c;這類 “時…
閱讀更多...
MAZANOKE+cpolar讓照片存儲無上限

MAZANOKE+cpolar讓照片存儲無上限

文章目錄前言1. 關于MAZANOKE2. Docker部署3. 簡單使用MAZANOKE4. 安裝cpolar內網穿透5. 配置公網地址6. 配置固定公網地址總結當工具開始理解用戶的需求痛點時&#xff0c;MAZANOKE與cpolar這對搭檔給出了“輕量化”的解決方案。它不追求浮夸的功能堆砌&#xff0c;卻用扎實的…
閱讀更多...
正則表達式 - 元字符

正則表達式 - 元字符

正則表達式中的元字符是具有特殊含義的字符&#xff0c;它們不表示字面意義&#xff0c;而是用于控制匹配模式。基本元字符. (點號)匹配除換行符(\n)外的任意單個字符示例&#xff1a;a.b 匹配 "aab", "a1b", "a b" 等^ (脫字符)匹配字符串的開始…
閱讀更多...
suricata源碼解讀-事務日志

suricata源碼解讀-事務日志

注冊事務日志線程模塊 void TmModuleTxLoggerRegister (void) {tmm_modules[TMM_TXLOGGER].name "__tx_logger__";tmm_modules[TMM_TXLOGGER].ThreadInit OutputTxLogThreadInit;tmm_modules[TMM_TXLOGGER].Func OutputTxLog;tmm_modules[TMM_TXLOGGER].ThreadExi…
閱讀更多...
【CSS】層疊上下文和z-index

【CSS】層疊上下文和z-index

z-index 的作用范圍受“層疊上下文&#xff08;stacking context&#xff09;”影響。&#x1f539; 1. z-index 的基本作用 控制元素在 同一個層疊上下文&#xff08;stacking context&#xff09; 內的堆疊順序。值越大&#xff0c;顯示層級越靠上。&#x1f539; 2. 什么是層…
閱讀更多...
自動化腳本的降本增效實踐

自動化腳本的降本增效實踐

一、自動化腳本的核心價值自動化腳本通過模擬人類操作完成重復性任務&#xff0c;其核心價值體現在三個維度&#xff1a;首先&#xff0c;在時間成本方面&#xff0c;標準化的數據處理流程可縮短90%以上的操作耗時&#xff1b;其次&#xff0c;在人力成本上&#xff0c;單個腳本…
閱讀更多...
【C語言】第七課 字符串與危險函數??

【C語言】第七課 字符串與危險函數??

C語言中的字符串處理既是基礎&#xff0c;也是安全漏洞的重災區。理解C風格字符串的底層原理及其危險函數的運作方式&#xff0c;對于編寫安全代碼和進行逆向工程分析至關重要。 &#x1f9e9; C風格字符串的本質 C風格字符串本質上是以空字符\0&#xff08;ASCII值為0&#xf…
閱讀更多...
Mac安裝hadoop

Mac安裝hadoop

1.在terminal中檢查是否安裝brew命令 brew --version 如果沒有安裝&#xff0c;在terminal中執行命令&#xff0c;安裝brew /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)" 安裝完成后&#xff0c;再重新打…
閱讀更多...
多語言編碼Agent解決方案（4）-Eclipse插件實現

多語言編碼Agent解決方案（4）-Eclipse插件實現

Eclipse插件實現&#xff1a;支持多語言的編碼Agent集成 本部分包含Eclipse插件的完整實現&#xff0c;包括多語言支持、命令注冊、API調用和UI集成。插件使用Java開發&#xff0c;基于Eclipse Plugin Development Environment (PDE)。 1. Eclipse插件目錄結構 eclipse-plugin/…
閱讀更多...
風險規則引擎-RPA 作為自動化依賴業務決策流程的強大工具

風險規則引擎-RPA 作為自動化依賴業務決策流程的強大工具

機器人流程自動化&#xff08;RPA&#xff09;聽起來好像跟機器人統治世界似的&#xff0c;但其實不是那么回事。RPA 就是一套能在電腦上運行的程序&#xff0c;能快速、高效地自動完成日常重復的工作。RPA 讓你能夠設置一些軟件“機器人”來執行特定的任務。RPA 的一個大好處就…
閱讀更多...
漏洞無效化學習

漏洞無效化學習

一、基礎概念與原理1. 核心定義漏洞無效化&#xff08;Vulnerability Mitigation&#xff09;&#xff1a;并非直接修補漏洞本身&#xff0c;而是通過技術手段降低漏洞被成功利用的概率。其目標是讓攻擊者即使發現漏洞也無法達成攻擊目的。 關鍵思路&#xff1a;通過訪問控制、…
閱讀更多...
「Vue 項目中實現智能時間選擇：帶業務規則的級聯選擇器」

「Vue 項目中實現智能時間選擇：帶業務規則的級聯選擇器」

#創作靈感公司業務需要&#xff0c;某個時間節點前可以選擇到月&#xff0c;某個時間節點后只能選擇季度vue2 Vant2javascriptimport { Cascader, Field, Form, Popup, Button } from vant; import vant/lib/index.css;export default {name: CascaderPage,components: {VanCa…
閱讀更多...
day1———Qt———應用程序界面設置

day1———Qt———應用程序界面設置

1&#xff0c;定義一個Mystring類代替string的功能#include <iostream> #include <string.h>using namespace std; class Mystring {friend ostream &operator<<(ostream &cout,const Mystring &s);friend istream &operator>>(istrea…
閱讀更多...
apache實現LAMP＋apache(URL重定向)

apache實現LAMP＋apache(URL重定向)

1.apache實現LAMPLAMP是指一組通常一起使用來運行動態網站的自由軟件名稱首字母的縮寫a.L是指Linux操作系統b,.A是指Apache&#xff0c;用來提供Web服務c.M指MySQL&#xff0c;用來提供數據庫服務d.P指PHP&#xff0c;是動態網站的一種開發語言1.1php運行方式說明php是腳本語言…
閱讀更多...
SAConv可切換空洞卷積

SAConv可切換空洞卷積

SAConv可切換空洞卷積 帶來的改進機制時可切換的空洞卷積 是一種創新型卷積網絡 專門為增強物體檢測和分割任務&#xff0c;中特征提取去設計 SAC核心時相同的輸入兒子應用到不同空洞率去進行卷積&#xff0c;設計特別開關函數融合這些不同卷積的成果 該方法可讓網絡更靈活的適…
閱讀更多...
基于Matlab的霧霾天氣和夜間車牌識別系統

基于Matlab的霧霾天氣和夜間車牌識別系統

在復雜天氣和低光照環境下&#xff0c;車牌識別系統的準確率和穩定性顯著下降&#xff0c;嚴重影響交通管理與智能監控的可靠性。本文針對霧霾天氣和夜間環境下車牌圖像特征模糊、對比度低、噪聲干擾嚴重的問題&#xff0c;提出了一種融合圖像增強與模板匹配的車牌識別方法。系…
閱讀更多...
華為云/本地化部署K8S-查看容器日志

華為云/本地化部署K8S-查看容器日志

華為云日志查看 目前工作的大部分情況下&#xff0c;通過華為云LTS云日志服務就可以滿足日常需求。 不過上線時過來支援的開發老哥更習慣于從容器里查看日志&#xff0c;也一并記錄下以備不時之需。 1.登錄服務節點服務器 點擊左側三個橫線&#xff0c;選擇 應用服務-云容器引擎…
閱讀更多...
【MySQL 死鎖：從 “業務卡頓“ 到 “根因定位“ 的實戰指南】

【MySQL 死鎖：從 “業務卡頓“ 到 “根因定位“ 的實戰指南】

MySQL 死鎖&#xff1a;從 “業務卡頓” 到 “根因定位” 的實戰指南 后端開發必看&#xff1a;MySQL死鎖排查與預防全攻略線上系統突然報出Deadlock found when trying to get lock; try restarting transaction&#xff0c;用戶操作卡頓甚至超時&#xff0c;排查時卻對著一堆…
閱讀更多...
從虛擬化基石到云原生架構的降維打擊：用dd/mkfs玩轉namespace隔離，解鎖Docker/K8S資源密碼，看透物理機到云服務器的進化之路

從虛擬化基石到云原生架構的降維打擊：用dd/mkfs玩轉namespace隔離，解鎖Docker/K8S資源密碼，看透物理機到云服務器的進化之路

本篇摘要 本文圍繞虛擬化與容器化技術展開&#xff0c;涵蓋架構演進、Docker/K8S優勢與挑戰、namespace隔離實操&#xff08;如主機名/PID隔離&#xff09;、磁盤操作&#xff08;dd/mkfs/df/mount&#xff09;等&#xff0c;對比虛擬機與容器差異&#xff0c;闡明技術原理與架…
閱讀更多...
自動化測試的概念

自動化測試的概念

文章目錄自動化測試能夠取代人工測試嗎&#xff1f;回歸測試自動化分類自動化測試金字塔為啥單元測試的性價比這么高呢&#xff1f;那為啥UI自動化測試的性價比沒有組件測試的高呢&#xff1f;web自動化測試舉例引入自動化測試的準備工作自動化測試的簡單示例自動化測試能夠取代…
閱讀更多...
最新文章

Copyright @ 2022~2023