目錄
引言:
MEX Count
? ? ? ? 題意分析
? ? ? ? 邏輯梳理
? ? ? ? 代碼實現
結語:
引言:
? ? ? ? 本來,今天我是想著出倆題或三題題解的,但是在打第一題的時候就天塌了,導致今天就只搓了一道題,這題的難度在CF中為1300的水準,但我感覺這題的難度實則不止1300,因為前幾天1400的題里,都沒有遇到這么棘手的,可能是我數學方面的能力不足,以至于這題耗費我巨大心力,而且,最惡心的是,這題的題目翻譯還翻譯錯了,導致我找錯誤找半天都沒找出來,具體下面會講,接下來,我們進入今天的題目講解----------->
?????????????????????????????????????????????????????????????
MEX Count
? ? ? ? 接下來,我們先來看題目
? ? ? ? 題意分析
? ? ? ? 這是題目的鏈接Problem - 2124C - Codeforces
? ? ? ? 不想跳轉的可看下圖

? ? ? ??
? ? ? ? 看完題目后,是不是很抽象,第一行就看不懂了,所以我又用了別的翻譯插件來翻譯這個題目,如圖
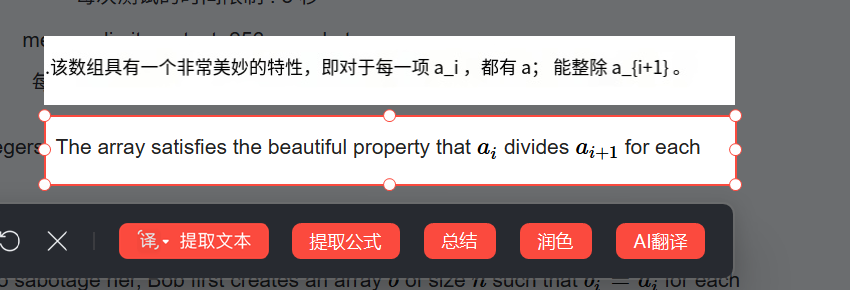
? ? ? ? 看這個翻譯是不是很明顯,就是ai可以整除ai+1,但好巧不巧,這個翻譯也是錯的,所以我遭不住了,題目的實際意思其實是,一個數組a,這個數組是i+1位置下的元素可以整除i位置下的元素
? ? ? ? 那么,這個弄清楚后,后面的翻譯就沒問題了,很清晰,就是對a數組進行操作,給定一個變量x,然后對a數組中的元素乘任意個數的x,得到一個新的數組b
? ? ? ? 題目輸入的就是這個數組b,然后讓我們求出可能得x中的任意一個值即可
? ? ? ? 那么,題目就講解完了,接下來我們進行邏輯梳理
? ? ? ? 邏輯梳理
? ? ? ? 首先,我們先來分析下a數組和b數組的區別
? ? ? ? 同一個下標下,b數組的元素是由a數組元素乘上未知個x得到的,因為是對a數組的元素進行乘的操作,所以b數組整體的最大公因數肯定不會低于a數組的最大公因數
? ? ? ? 我們再來思考下還有啥能找的現成的,那就還有相鄰下標下a元素變成b元素的方式若不同對公因數的影響
? ? ? ? 第一種 i 下標的a元素和?i+1下標下的a元素都不乘x,這時這倆個的公因數無變化
? ? ? ? 第二種 i 下標的a元素乘了x,i+1下標下的a元素沒乘x。或反之,這種情況下,倆個的公因數亦沒有變化
? ? ? ? 第三種 i和i+1下標下的a元素都乘了x,這時候,公因數就會變大了
? ? ? ? 那么,通過這三種情況,我們先來假設第一種情況
? ? ? ? b數組如果本來就是a數組,那么這個時候因為a數組中臨近的下一個元素總是他前面元素的倍數,所以我們可以從后往前進行遍歷,通過一次次的迭代最小公約數,然后尋找最大公倍數來得到可能得x。講起來很抽象,那么,我們來通過圖文來理解
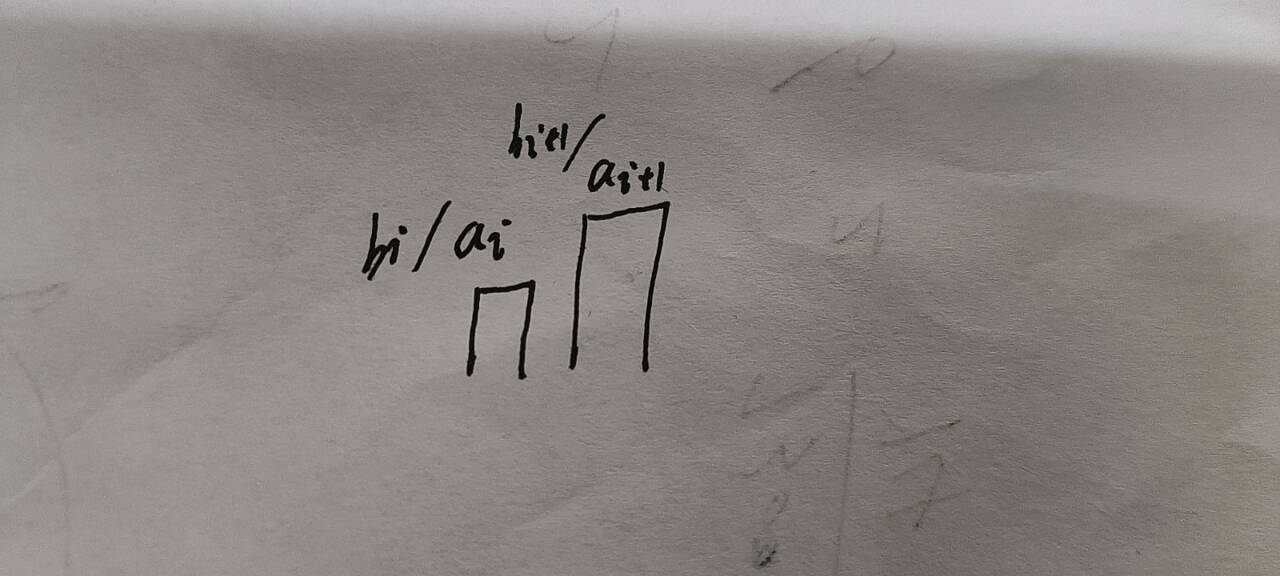
? ? ? ? 如圖。因為現在是第一種情況,所以a數組的數據即為b數組的數據,那么,我們將ai與ai+1的元素進行取最大公因數,得到的就是ai,然后我們再將上一次得到的最小公倍數與ai/現在的最大公因數 這倆個數進行求最小公倍數的操作得到一個新的最小公倍數(這個即到目前為止,不看前面的元素,可以使用的最小的x)
? ? ? ? 這種我們可以把他當做是那種將一個大份的元素拆解成一個個小份的元素進行一次次演算,得到每次的最佳值,再用最佳值去進行操作即可,直到走到底部為止
? ? ? ? 那為什么進行先前最小公倍數與ai/現在的最大公因數來求這次的最小公倍數這個操作得到的最小公倍數就是滿足條件的值呢,那我們來徐徐道來
? ? ? ? 先前的最小公倍數? ? 即只管后面那些數組時,x的最小值
? ? ? ? ai/現在的最大公因數? ? ? ? 即該下標下的這個元素的剩余的因數
? ? ? ? 如果想要乘任意次來達到數據的變化條件,就需要得到上面倆個數據的最小公倍數,這樣就可以使加上當前下標后的數組也滿足使用x來達到現在的b數組
? ? ? ? 所以就一路推下去就好了
? ? ? ? 其余倆種情況也是同理,原理我上面也講的差不多了,太過玄乎了,所以這里就不展開講了,這個的邏輯是否完全準確我也沒有把握,但是我把我能想到的情況都推敲了下,都沒什么問題,代碼也AC了,接下來,邏輯梳理講完了,我們來進入代碼實現的環節。?
???????? ? ? 代碼實現
? ? ? ? ? ? ? ? 上面的邏輯理清楚后,代碼實現其實就很簡單了,只需要打一個求最大公約數的函數和一個求最小公倍數的函數就可以了,然后再循環里調用一下就好了,gcd函數為最大公約數,lcm函數為最小公倍數,求這倆個數的函數應該都會實現吧,這里就不講了,接下來就上AC源代碼啦
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <vector>
using namespace std;int t;
long long a[600010];long long gcd(long long x, long long y)
{if (y == 0)return x;return gcd(y, x % y);
}long long lcm(long long x,long long y)
{long long k = gcd(x, y);return x / k * y;
}void solve()
{long long Gcd = 0;long long Lcm = 1;int n;a[0] = 1;cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];}for (int i = n; i > 0; i--){Gcd = gcd(Gcd, a[i]);Lcm = lcm(Lcm, a[i] / Gcd);}cout << Lcm << endl;
}int main()
{cin >> t;while (t--){solve();}return 0;
}? ? ? ? 那么,這題就講完啦
結語:
? ? ? ? 今日算法講解到此結束啦,希望對你們有所幫助,謝謝觀看,如果覺得不錯可以分享給朋友喲。但不得不說,這題是真的折磨,燃盡了,一個1300的題花的時間比2道1400的題還久






)







------休眠函數sleep_for和sleep_until)





