強化學習-CH9 策略梯度方法

當策略被表示為函數時，通過優化目標函數可以得到最優策略。 這種方法稱為策略梯度。策略梯度方法是基于策略的，而之前介紹的方法都是基于值的。其本質區別在于基于策略的方法是直接優化關于策略參數的目標函數。

9.1 策略表示：從表格到函數

表格形式：

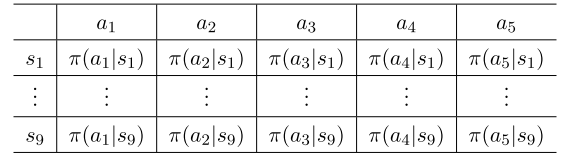
函數形式：

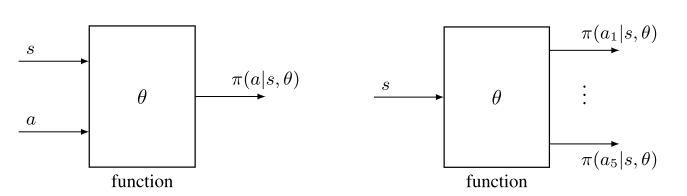
區別：

（1）定義最優策略：當用表格表示時，如果策略可以最大化每個狀態值，即其狀態值大于或等于其他任意策略的狀態值，則將其定義為最優策略。 當用函數表示時，如果策略可以最大化一個標量目標函數，則將其定義為最優策略。

（2）更新政策：當用表格表示時，可以通過直接更改表中的條目來更新策略。 當用參數化函數表示策略時，不能再以這種方式更新策略。 相反，它只能通過改變參數θ來更新。

（3）檢索一個動作的概率： 在表格的情況下，可以通過查找表中的相應條目直接獲得動作的概率。 在函數表示的情況下，需要在函數中輸入（s, a）來計算其概率。

9.2 目標函數：定義最優策略

目標函數1：平均狀態值

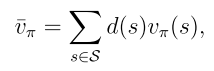
d(s)是狀態s的權重，也可以理解為狀態s的概率分布，因此可以重寫為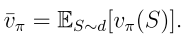

如何選擇d(s):

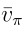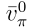（1）第一種也是最簡單的情況是d與策略π無關。 在這種情況下，將d表示為d0，并將表示為，以表明分布與策略無關。

（2）第二種情況是d依賴于策略π。 在這種情況下，通常選擇d為dπ，它是π下的平穩分布。

等價表達式：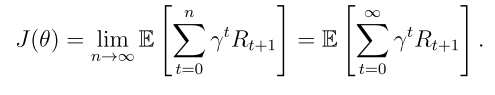

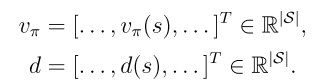
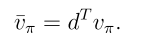
目標函數2：平均獎勵

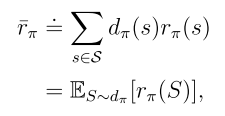
其中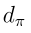是平穩分布，且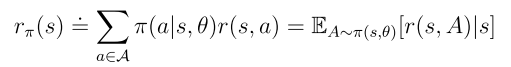是從狀態s出發的即時獎勵的期望值。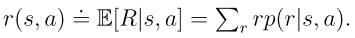

等價表達式：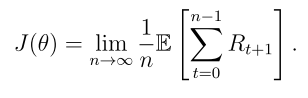

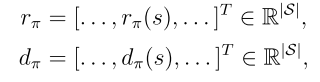
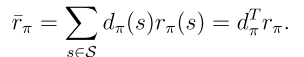
所有這些目標函數都是π的函數。 因為π是由θ參數化的，所以這些函數是θ的函數。 換句話說，不同的θ值可以產生不同的目標函數值。因此，可以尋找θ的最優值來最大化這些函數值。 這是策略梯度方法的基本思想。

9.3 目標函數的梯度

定理9.1（策略梯度定理）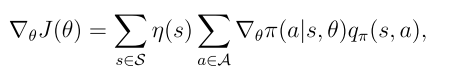

等價形式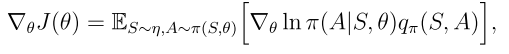

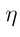是狀態的概率分布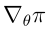，是π關于θ的梯度

9.4 蒙特卡羅策略梯度

用梯度上升算法來最大化目標函數以獲得最佳策略

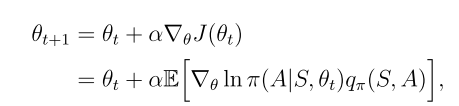
用隨機梯度替換真實梯度

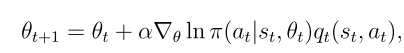
20150037)]

用隨機梯度替換真實梯度

[外鏈圖片轉存中…(img-Sa4XqvJh-1757420150037)]