基于胎兒Y染色體濃度的孕周與BMI建模分析
摘要
本文利用某競賽提供的胎兒Y染色體濃度數據,建立了以孕周和孕婦BMI為自變量的多項式回歸模型,探討了其對Y染色體濃度的影響。通過數據清洗與篩選,共獲得1082條有效男胎樣本。結果顯示:Y染色體濃度隨孕周顯著上升,BMI對濃度也存在非線性效應。嵌套F檢驗表明引入BMI及其二次項顯著提升模型擬合效果(p < 0.001)。該研究為無創產前檢測(NIPT)中合理確定檢測時機與人群分層提供了方法學依據。
1 引言
胎兒游離DNA濃度是無創產前檢測準確性的關鍵指標。既往研究表明,胎兒Y染色體濃度與孕周呈正相關,但不同孕婦個體特征(如BMI)可能影響該關系。本文基于競賽公開數據,采用數理建模方法,系統分析孕周、BMI與Y染色體濃度之間的關系,并探索BMI分組與檢測時點優化的可行性。
2 數據與方法
2.1 數據來源與處理
原始數據為某醫療檢測機構提供的臨床檢測記錄,包含孕周、孕婦BMI、Y染色體濃度等指標。
孕周解析:如“12+3”統一轉化為12.43周。
男胎判定:若Y濃度或Y染色體Z值非空,即判定為男胎。
濃度統一:將Y染色體濃度統一轉換為比例數值(0–1區間)。
最終篩選得到1082例男胎樣本。
Step 1|讀取數據與字段檢查
#?Step?1:讀取?Excel?&?初步字段核對
import?pandas?as?pd
from?pathlib?import?PathDATA_XLSX?=?Path("附件.xlsx")??#?←改成你的路徑xls?=?pd.ExcelFile(DATA_XLSX)
sheet_name?=?xls.sheet_names[0]???????#?默認第一張表
df_raw?=?pd.read_excel(DATA_XLSX,?sheet_name=sheet_name)
df_raw.columns?=?[str(c).strip()?for?c?in?df_raw.columns]print("工作表:",?sheet_name)
print("列名:",?list(df_raw.columns))
df_raw.head(10)
Step 2|數據清洗與派生字段
#?Step?2:數據清洗與派生
import?numpy?as?np
import?redf?=?df_raw.copy()def?parse_gest_week(x):"""將?'12+3'/'12周+3天'/12?等解析為“周”的浮點數。"""if?pd.isna(x):return?np.nanif?isinstance(x,?(int,?float)):return?float(x)s?=?str(x)m?=?re.search(r'(\d+)\D+(\d+)',?s)???#?有“周+天”的情況if?m:w?=?float(m.group(1));?d?=?float(m.group(2))return?w?+?d/7.0m?=?re.search(r'(\d+)',?s)???????????#?只有周if?m:return?float(m.group(1))return?np.nan#?標準化字段
df["孕周_周"]??=?df["檢測孕周"].apply(parse_gest_week)
df["BMI"]?????=?pd.to_numeric(df["孕婦BMI"],?errors="coerce")
df["Y濃度_raw"]?=?pd.to_numeric(df["Y染色體濃度"],?errors="coerce")
df["ZY"]??????=?pd.to_numeric(df["Y染色體的Z值"],?errors="coerce")#?男胎判定(保守):Y濃度?或?ZY?任一非空
is_male?=?df["Y濃度_raw"].notna()?|?df["ZY"].notna()#?量綱判斷:若>1?的比例?>50%,視為百分數(如?7?表示?7%)
gt1_ratio?=?(df.loc[is_male,?"Y濃度_raw"]?>?1).mean()
df["Y濃度"]?=?(df["Y濃度_raw"]/100.0)?if?gt1_ratio?>?0.5?else?df["Y濃度_raw"].astype(float)#?建模子集:三要素齊全
df_model?=?df.loc[is_male].copy()
df_model?=?df_model[df_model["孕周_周"].notna()?&?df_model["BMI"].notna()?&?df_model["Y濃度"].notna()
].copy()summary?=?pd.DataFrame([{"總樣本數":?len(df),"男胎樣本數(判定)":?int(is_male.sum()),"用于建模樣本數":?len(df_model),"孕周均值":?round(df_model["孕周_周"].mean(),?3),"孕周范圍":?f'{df_model["孕周_周"].min():.1f}?~?{df_model["孕周_周"].max():.1f}',"BMI均值":?round(df_model["BMI"].mean(),?3),"BMI范圍":?f'{df_model["BMI"].min():.1f}?~?{df_model["BMI"].max():.1f}',"Y濃度是否多數為百分數":?bool(gt1_ratio?>?0.5),"Y濃度均值(比例)":?round(df_model["Y濃度"].mean(),?4)
}])
summary.to_csv(OUT_DIR/"Step2_清洗后樣本摘要.csv",?index=False,?encoding="utf-8-sig")
summary
2.2 探索性分析
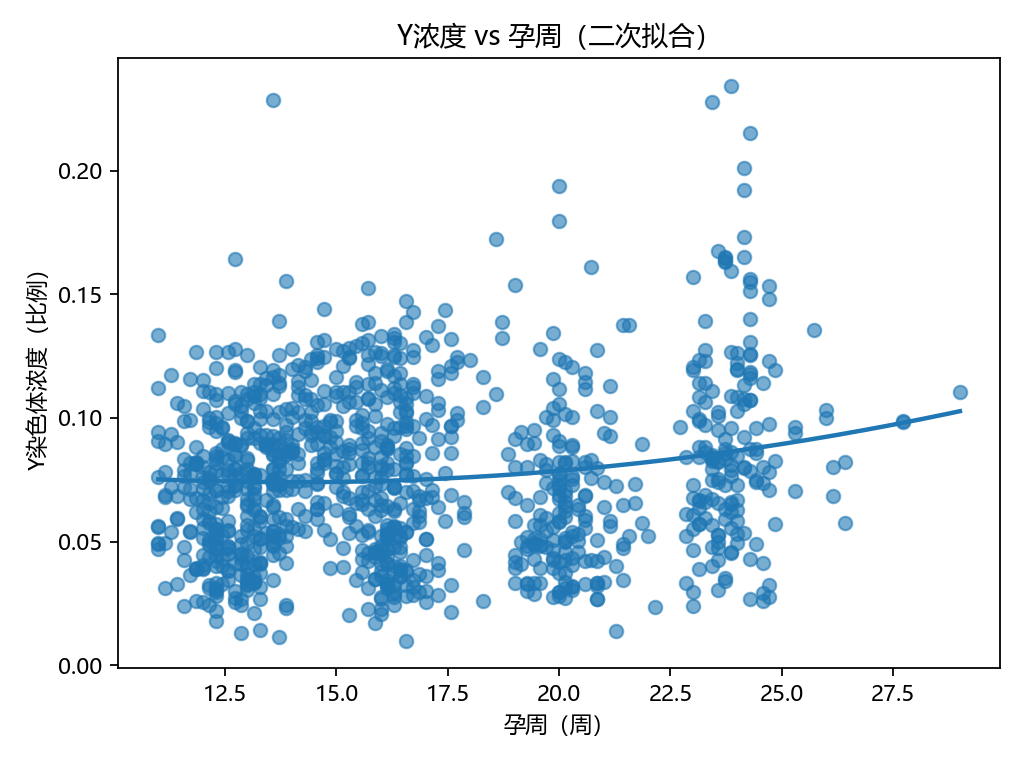
繪制孕周與Y濃度散點圖,觀察非線性趨勢。
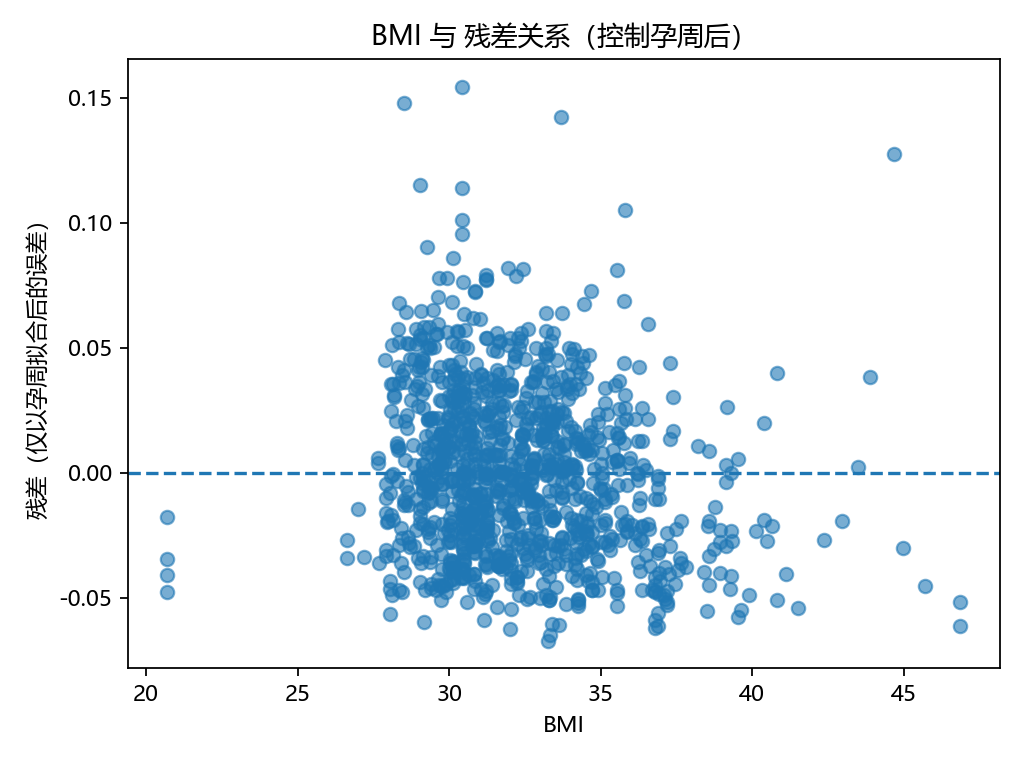
計算控制孕周后的殘差與BMI的相關性。
對比不同BMI分組下的Y濃度分布。
#?Step?3:EDA?可視化(中文無亂碼)
import?matplotlib.pyplot?as?plt
import?numpy?as?np
from?sklearn.linear_model?import?LinearRegression
from?sklearn.preprocessing?import?PolynomialFeaturesdef?savefig(path):plt.tight_layout()plt.savefig(path,?dpi=160)plt.close()#?3-1?直方圖:孕周、BMI、Y濃度
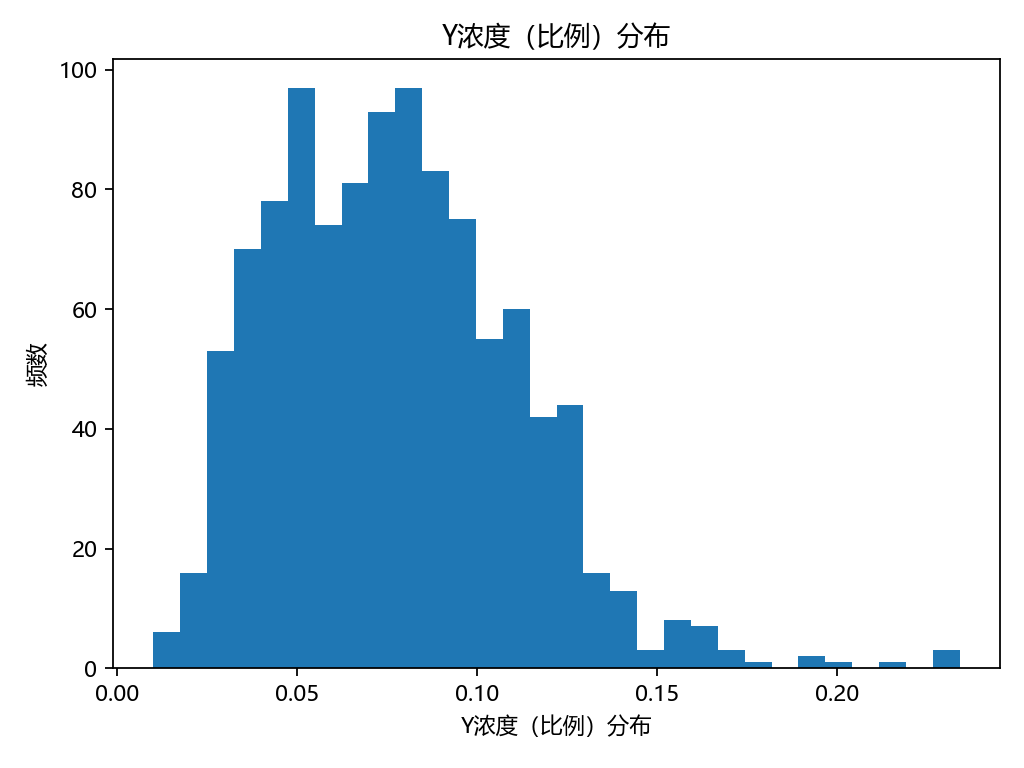
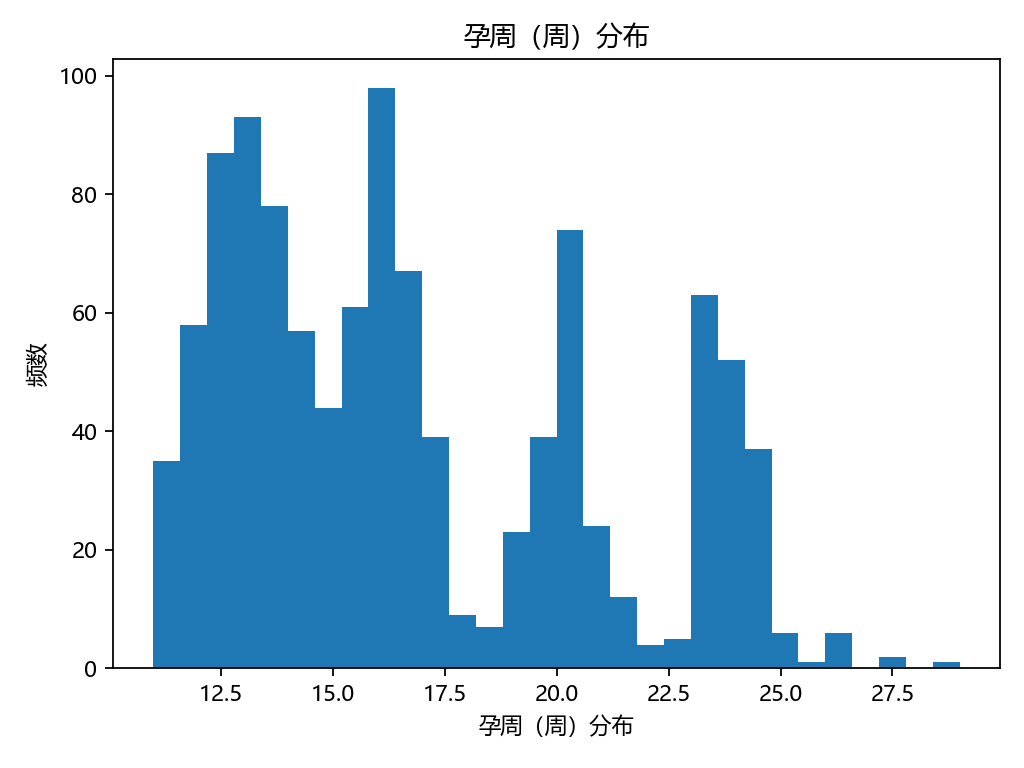
for?col,?title?in?[("孕周_周","孕周(周)分布"),?("BMI","BMI?分布"),?("Y濃度","Y濃度(比例)分布")]:plt.figure()plt.hist(df_model[col].values,?bins=30)plt.xlabel(title);?plt.ylabel("頻數");?plt.title(title)savefig(OUT_DIR?/?f"Step3_{col}_hist.png")#?3-2?散點?+?二次擬合:Y?vs?孕周(只看形狀)
GA?=?df_model["孕周_周"].astype(float).values
Y??=?df_model["Y濃度"].astype(float).valuesplt.figure()
plt.scatter(GA,?Y,?alpha=0.6)
coefs?=?np.polyfit(GA,?Y,?deg=2)
xx?=?np.linspace(np.nanmin(GA),?np.nanmax(GA),?200)
yy?=?np.polyval(coefs,?xx)
plt.plot(xx,?yy,?linewidth=2)
plt.xlabel("孕周(周)");?plt.ylabel("Y染色體濃度(比例)");?plt.title("Y濃度?vs?孕周(二次擬合)")
savefig(OUT_DIR?/?"Step3_Y_vs_GA_quadratic.png")#?3-3?控制孕周后的殘差?vs?BMI(僅孕周二次項擬合)
pf?=?PolynomialFeatures(degree=2,?include_bias=False)
X_ga?=?pf.fit_transform(GA.reshape(-1,1))
lr?=?LinearRegression().fit(X_ga,?Y)
resid?=?Y?-?lr.predict(X_ga)plt.figure()
plt.scatter(df_model["BMI"].values,?resid,?alpha=0.6)
plt.axhline(0,?linestyle="--")
plt.xlabel("BMI");?plt.ylabel("殘差(僅以孕周擬合后的誤差)")
plt.title("BMI?與?殘差關系(控制孕周后)")
savefig(OUT_DIR?/?"Step3_resid_vs_BMI.png")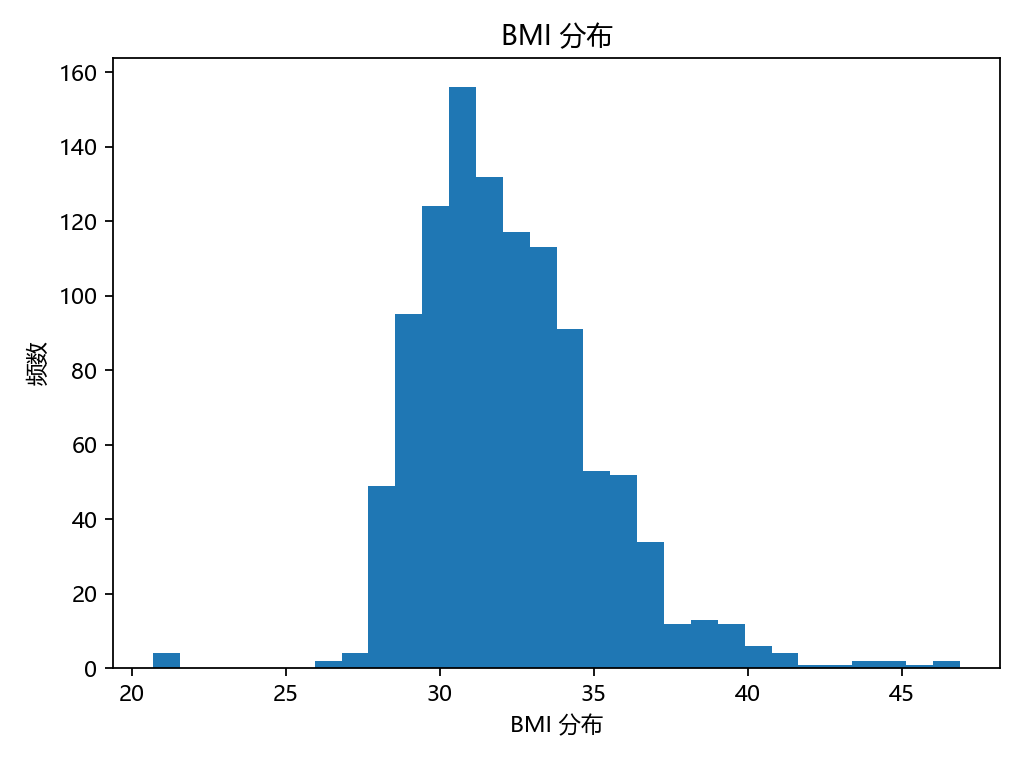
2.3 模型構建
設孕周為 ,BMI為 ,Y濃度為 。構建二次多項式模型:
采用最小二乘法估計參數,并通過嵌套F檢驗比較基線模型(僅含孕周二次項)與完整模型。
#?Step?4:模型對比(嵌套F檢驗)
import?statsmodels.api?as?sm
import?pandas?as?pdGA?=?df_model["孕周_周"].astype(float).values
BMI?=?df_model["BMI"].astype(float).values
Y??=?df_model["Y濃度"].astype(float).values#?簡化模型:const?+?GA?+?GA^2
X1?=?pd.DataFrame({"const":?1.0,?"GA":?GA})
X1["GA^2"]?=?X1["GA"]**2
m1?=?sm.OLS(Y,?X1.values).fit()#?完整模型:const?+?GA?+?BMI?+?GA^2?+?GA*BMI?+?BMI^2
X2?=?pd.DataFrame({"const":?1.0,?"GA":?GA,?"BMI":?BMI})
X2["GA^2"]?=?X2["GA"]**2
X2["GA*BMI"]?=?X2["GA"]?*?X2["BMI"]
X2["BMI^2"]?=?X2["BMI"]**2
m2?=?sm.OLS(Y,?X2.values).fit()fstat,?fpval,?df_diff?=?m2.compare_f_test(m1)model_compare?=?pd.DataFrame([{"簡化模型_R2(僅孕周二次)":?round(float(m1.rsquared),?4),"完整模型_R2(加BMI及交互二次)":?round(float(m2.rsquared),?4),"嵌套F統計量":?round(float(fstat),?4),"p值":?fpval,"自由度差":?int(df_diff)
}])
model_compare.to_csv(OUT_DIR/"Step4_模型對比.csv",?index=False,?encoding="utf-8-sig")
model_compare
2.4 模型評估
使用5折交叉驗證計算平均 。
繪制殘差圖、QQ圖檢驗正態性與異方差性。
針對閾值濃度(4%),反解預測方程以估計不同BMI下的“最早達標孕周”。
#?Step?5:完整模型系數與顯著性?+?文本報告
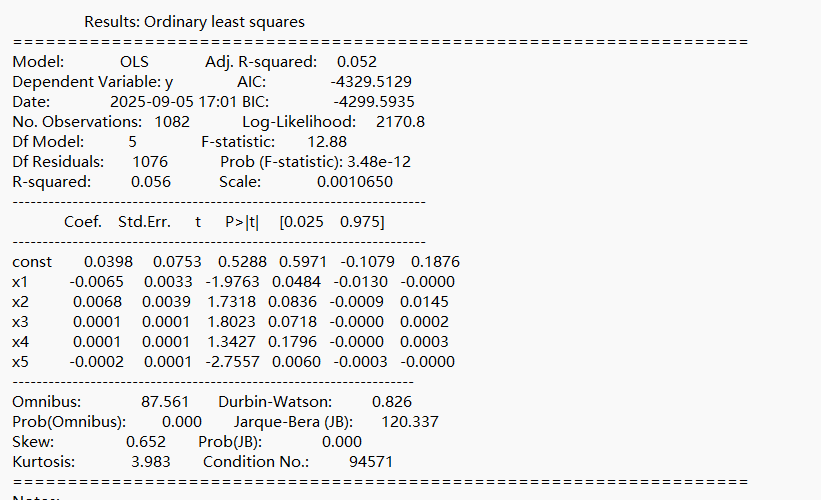
coef_table?=?pd.DataFrame({"變量":?["const","GA","BMI","GA^2","GA*BMI","BMI^2"],"系數":?list(m2.params),"p值":?list(m2.pvalues)
})
coef_table_rounded?=?coef_table.copy()
coef_table_rounded["系數"]?=?coef_table_rounded["系數"].round(8)
coef_table_rounded.to_csv(OUT_DIR/"Step5_完整模型_系數與顯著性.csv",?index=False,?encoding="utf-8-sig")with?open(OUT_DIR/"Step5_完整模型_OLS報告.txt",?"w",?encoding="utf-8")?as?f:f.write(m2.summary2().as_text())coef_table_rounded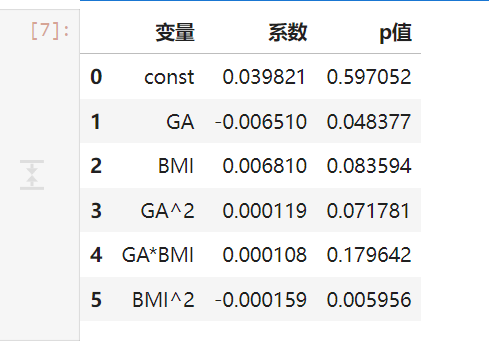
3 結果
3.1 樣本特征
孕周均值:16.85周(范圍11–29周);
BMI均值:32.29(范圍20.7–46.9);
Y濃度均值:7.7%(范圍1%–23%)。
3.2 回歸結果
模型估計系數如下:
孕周一次項顯著(p≈0.048);
BMI二次項顯著(p≈0.006),呈“先升后降”趨勢;
BMI與孕周交互項未顯著。
嵌套F檢驗:加入BMI項后模型擬合度顯著提升(p < 1e-8)。 5折交叉驗證 ,提示模型可解釋部分變異。
#?Step?6:5折交叉驗證
import?numpy?as?np
from?sklearn.preprocessing?import?PolynomialFeatures,?StandardScaler
from?sklearn.pipeline?import?make_pipeline
from?sklearn.linear_model?import?LinearRegression
from?sklearn.model_selection?import?KFold,?cross_val_scoreX?=?df_model[["孕周_周","BMI"]].astype(float).values
y?=?df_model["Y濃度"].astype(float).valuespipe?=?make_pipeline(PolynomialFeatures(degree=2,?include_bias=False),StandardScaler(with_mean=False),LinearRegression()
)cv?=?KFold(n_splits=5,?shuffle=True,?random_state=42)
r2_cv?=?cross_val_score(pipe,?X,?y,?cv=cv,?scoring="r2")cv_table?=?pd.DataFrame([{"5折CV_R2_均值":?float(np.mean(r2_cv)),"5折CV_R2_STD":?float(np.std(r2_cv))
}])
cv_table.to_csv(OUT_DIR/"Step6_5折CV_R2.csv",?index=False,?encoding="utf-8-sig")
cv_table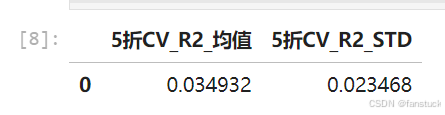
3.3 可視化結果
孕周與Y濃度曲線:非線性上升趨勢明顯。
不同BMI預測曲線:高BMI組整體推遲達標孕周。
模型診斷:殘差大致符合正態,異方差性有限。
#?Step?7:分層預測曲線(中文標簽)
import?numpy?as?np
import?matplotlib.pyplot?as?pltcoef?=?dict(zip(["const","GA","BMI","GA^2","GA*BMI","BMI^2"],?m2.params))def?predict_y(ga,?bmi):return?(coef["const"]+?coef["GA"]*ga+?coef["BMI"]*bmi+?coef["GA^2"]*ga*ga+?coef["GA*BMI"]*ga*bmi+?coef["BMI^2"]*bmi*bmi)xx?=?np.linspace(GA.min(),?GA.max(),?200)
bmi_levels?=?[28,?32,?36,?40]plt.figure()
for?b?in?bmi_levels:yy?=?[predict_y(g,?b)?for?g?in?xx]plt.plot(xx,?yy,?label=f"BMI={b}")
plt.axhline(0.04,?linestyle="--")
plt.xlabel("孕周(周)");?plt.ylabel("預測Y濃度(比例)")
plt.title("不同BMI下:預測Y濃度-孕周曲線(完整模型)")
plt.legend()
plt.tight_layout()
plt.savefig(OUT_DIR?/?"Step7_不同BMI_預測曲線.png",?dpi=160)
plt.close()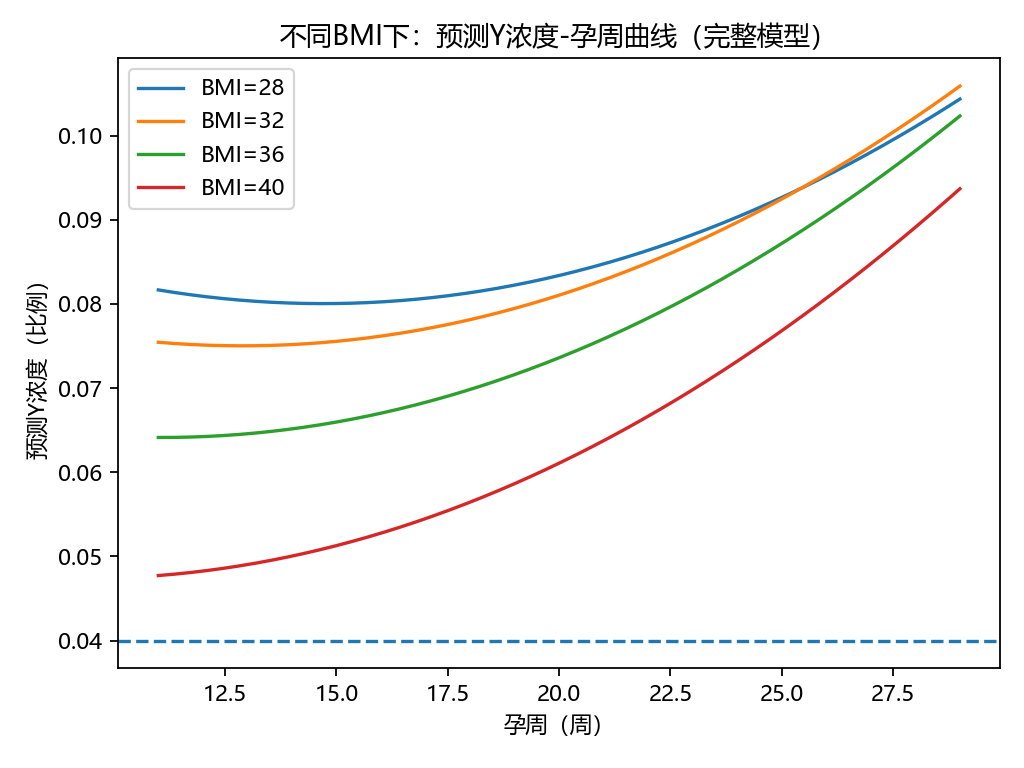
4 結論
結果表明,孕周是影響胎兒Y濃度的主要因素,而BMI對濃度存在非線性調節作用。對于BMI偏高的孕婦,可能需要更晚的孕周才能達到NIPT所需的最低濃度閾值。這與臨床觀察一致。研究發現:孕周顯著正向影響濃度,BMI具有非線性效應。該模型可為NIPT檢測時機與分層策略提供量化參考。
4.1模型診斷
#?Step?8:模型診斷
import?matplotlib.pyplot?as?plt
import?statsmodels.api?as?sm
from?statsmodels.stats.diagnostic?import?het_breuschpagany_hat?=?m2.fittedvalues
resid??=?m2.resid#?8-1?殘差?vs?擬合值
plt.figure()
plt.scatter(y_hat,?resid,?alpha=0.6)
plt.axhline(0,?linestyle="--")
plt.xlabel("擬合值");?plt.ylabel("殘差")
plt.title("殘差?vs?擬合值(完整模型)")
plt.tight_layout()
plt.savefig(OUT_DIR?/?"Step8_殘差_vs_擬合值.png",?dpi=160)
plt.close()#?8-2?QQ?圖
fig?=?sm.qqplot(resid,?line='45',?fit=True)
plt.title("QQ圖(殘差)")
plt.tight_layout()
plt.savefig(OUT_DIR?/?"Step8_QQPlot_殘差.png",?dpi=160)
plt.close()#?8-3?異方差檢驗(Breusch-Pagan)
exog?=?X2.values
bp_stat,?bp_pval,?_,?_?=?het_breuschpagan(resid,?exog)
bp_table?=?pd.DataFrame([{"BP統計量":?float(bp_stat),?"BP_p值":?float(bp_pval)}])
bp_table.to_csv(OUT_DIR/"Step8_BP異方差檢驗.csv",?index=False,?encoding="utf-8-sig")
bp_table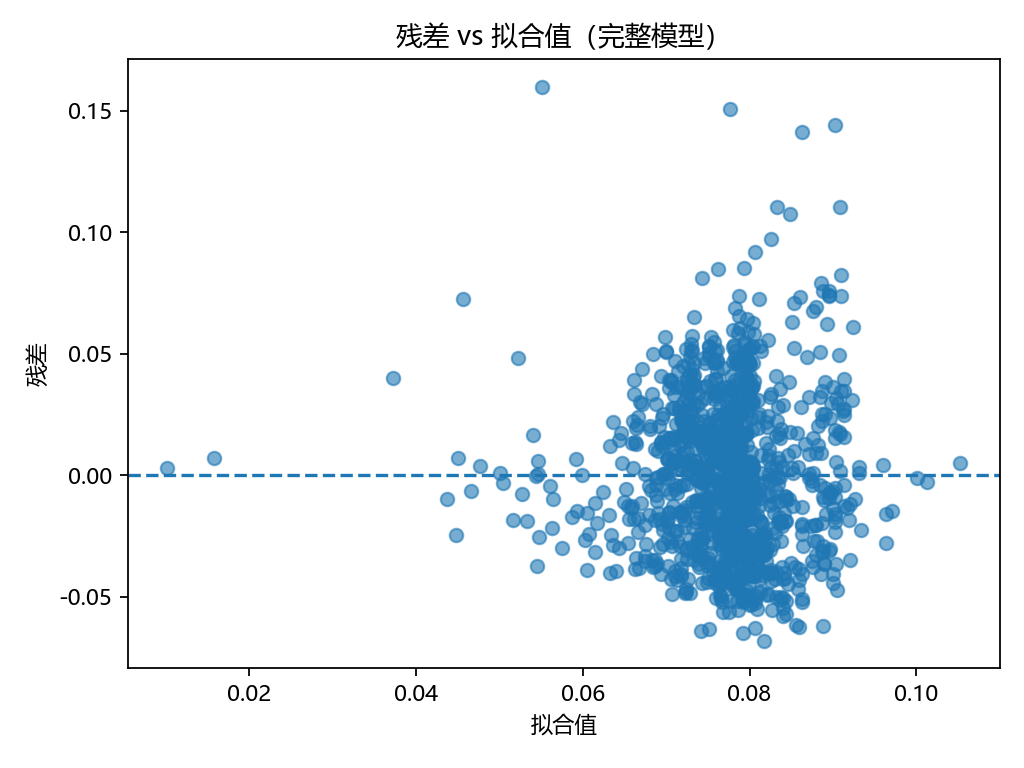
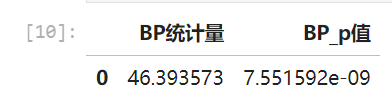
異方差性檢驗(BP檢驗)
BP統計量:46.39,p值≈7.6e-09
結論:p值遠小于0.05,說明殘差存在顯著的異方差性。即不同擬合值范圍下殘差方差不均一,違反了經典OLS假設。
殘差 vs 擬合值圖
- 圖像特點:
殘差大部分集中在0附近,但隨著擬合值增大,殘差的離散程度明顯增大。
出現了典型的“喇叭口”現象,進一步佐證了異方差問題。
啟示:說明模型預測在Y濃度較低區間比較穩定,但在較高區間波動較大,可能受BMI或其他未觀測變量影響。
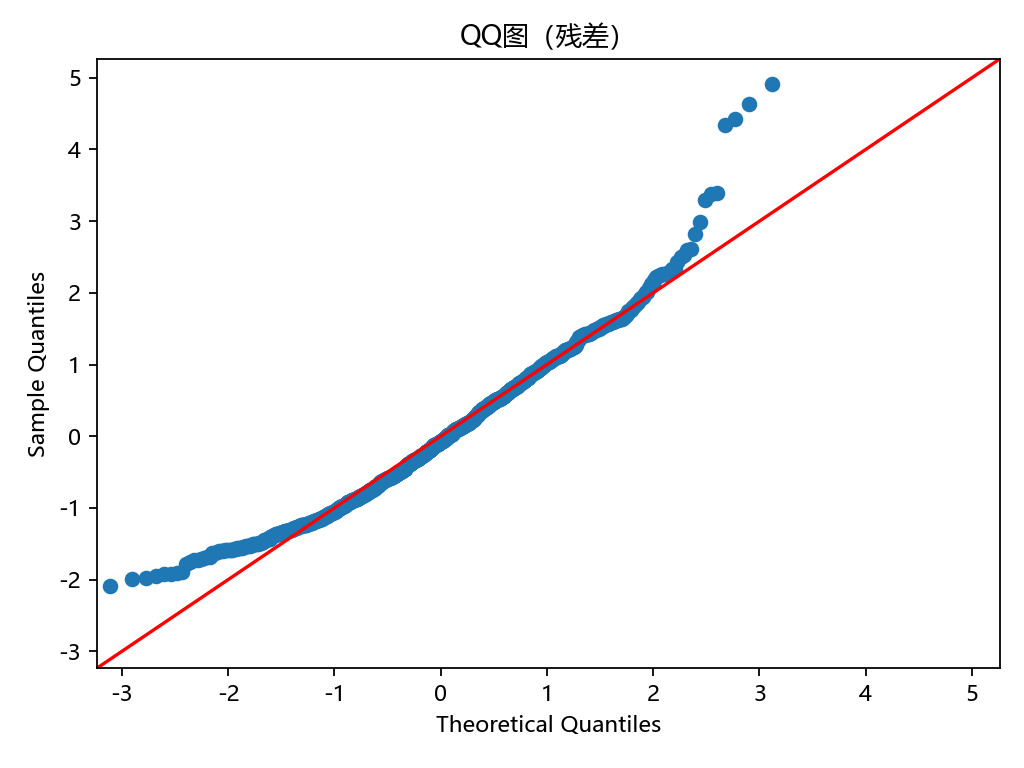
QQ圖(殘差正態性檢驗)
- 圖像特點:
殘差大部分點貼近對角線,表明殘差整體分布接近正態。
在尾部(特別是右上角),點明顯偏離直線,說明殘差存在重尾分布,即極端值比正態分布下更多。
啟示:模型正態性大致可接受,但尾部偏離提示少數極端樣本可能對回歸有較大影響。
殘差基本居中,正態性大致成立,說明模型能捕捉主要趨勢。




 --- 多表連接查詢篇)


---出現interactive_timeout/wait_timeout)


)



)




