【排序算法】④堆排序

系列文章目錄

?第一篇：【排序算法】①直接插入排序-CSDN博客

第二篇：【排序算法】②希爾排序-CSDN博客

第三篇：【排序算法】③直接選擇排序-CSDN博客

第四篇：【排序算法】④堆排序-CSDN博客

第五篇：【排序算法】⑤冒泡排序-CSDN博客

第六篇：【排序算法】⑥快速排序：Hoare、挖坑法、前后指針法-CSDN博客

第七篇：【排序算法】⑦歸并排序-CSDN博客

目錄

系列文章目錄

前言

一、堆是什么？

二、實現堆排序

1.堆排序所需要的堆函數

HeapCreate：堆的構建

核心算法BigADjustUp：(大堆)向上調整算法

HeapPopBig：刪除節點

核心算法BigADjustDown：向下調整算法

HeapDestory：堆的銷毀

2.堆排序代碼

三、分析堆排序

總結

前言

堆排序是指利用二叉樹（堆）這種數據結構所設計的一種排序算法，它是選擇排序的一種。

值得注意的是：排升序要建大堆，排降序建小堆。

一、堆是什么？

想要了解堆是什么，首先需要明白什么是完全二叉樹

完全二叉樹：

1. 二叉樹：由一個根節點加上兩棵別稱為左子樹和右子樹的二叉樹組成。

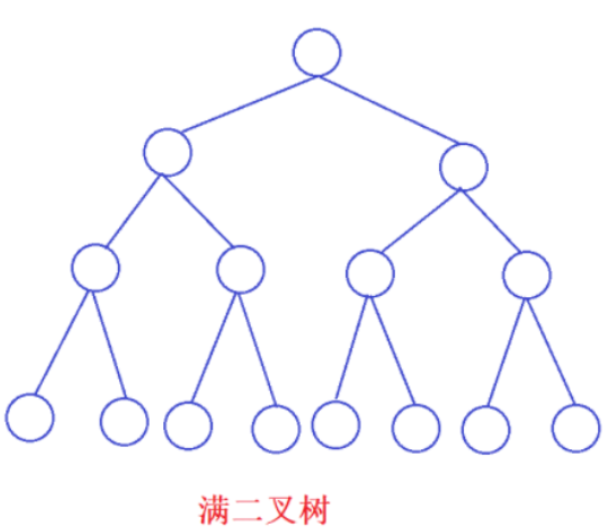
2. 滿二叉樹：一個二叉樹，如果每一個層的結點數都達到最大值，則這個二叉樹就是滿二叉樹。
3. 完全二叉樹：完全二叉樹是效率很高的數據結構，完全二叉樹是由滿二叉樹而引出來的。對于深度為K的，有n個結點的二叉樹，當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。要注意的是滿二叉樹是一種特殊的完全二叉樹。

堆的定義：

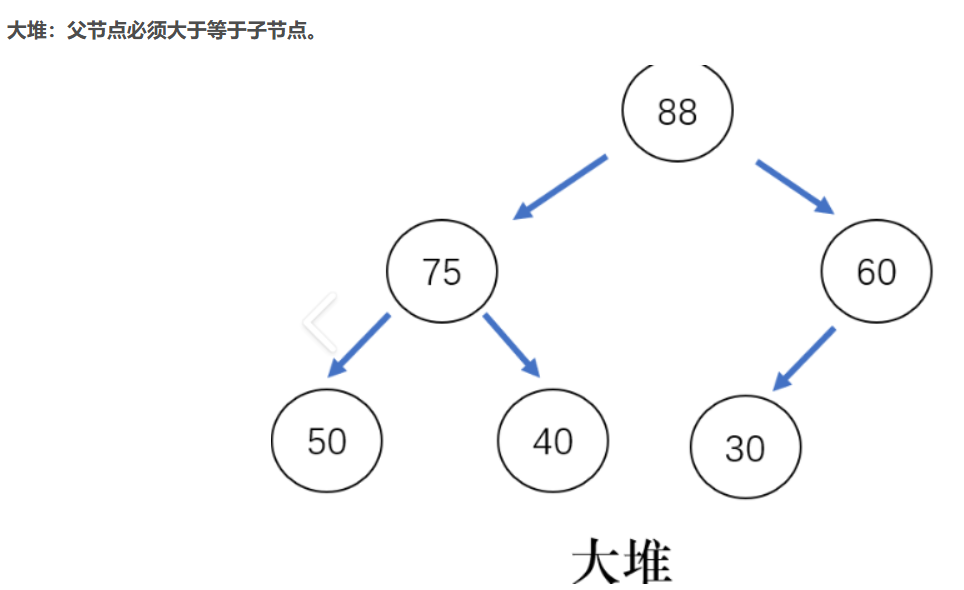
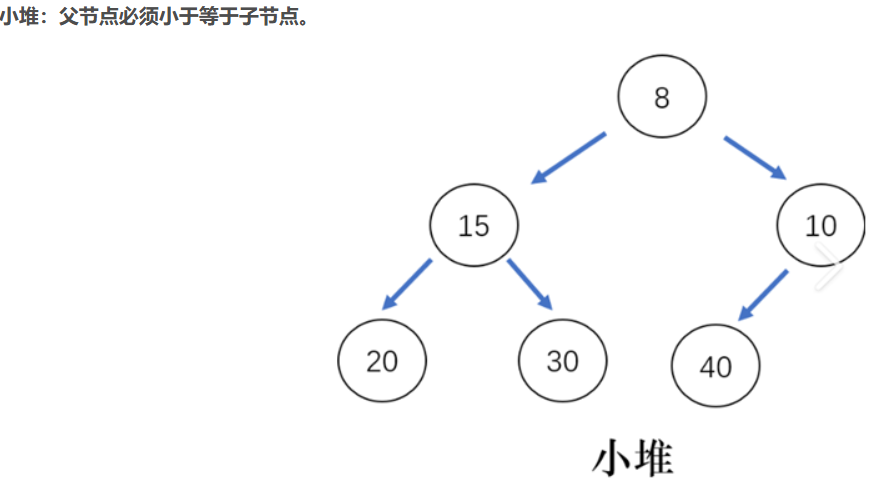
如果有一個碼的集合K = {k0 ，k1 ，k2 ，…，kn-1 }，把它的所有元素按完全二叉樹的順序存儲方式存儲在一個一維數組中，并滿足：ki <= k2i+1且ki <= k2i+2( ki>=k2i+1 且ki >=k2i+2 ) i = 0，1，2…，則稱為小堆(或大堆).

簡單來說：

完全二叉樹由于其性質非常適合使用順序結構存儲，所以，現實中我們通常把堆使用順序結構的數組來存儲。

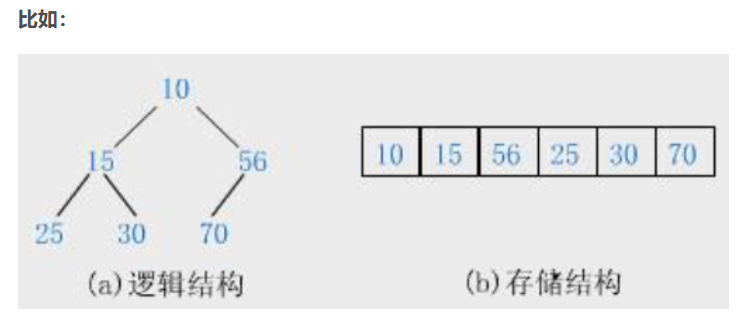
于是我們可以推出堆的數據結構：

typedef int HPDataType;typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;

上面是簡述堆的概念，目的是為堆排序準備。若是之前未接觸過堆這種數據結構的讀者，強烈建議先看看鏈接文章：【數據結構】二叉樹①-堆-CSDN博客

二、實現堆排序

本文以外部建堆實現堆排升序為例進行介紹，至于本地建堆或者堆排降序由于核心思想未變，可同理得出。

1.堆排序所需要的堆函數

HeapCreate：堆的構建

通過傳入數組a和數據個數nums，直接將傳入的數組構造成小堆。

// 堆的初始化，并構建傳入數組：為堆排序
void HeapCreateBig(Heap* hp, HPDataType* a, int nums)
{if(!hp||!a)return;HPDataType* temp = (HPDataType*)malloc(sizeof(HPDataType) * nums);if (temp){hp->_a = temp;hp->_capacity = nums;hp->_size = nums;}else{perror("HeapCreate malloc fail");exit(-1);}for (int i = 0; i < nums; ++i){hp->_a[i] = a[i];BigADjustUp(hp, i);}
}

上述代碼的核心在于最后的for循環：

①在循環中，將外部a數組的數據一個一個賦予給malloc出來堆中的數組；

②每賦予一個值，便調用依次BigADjustUp函數。

核心算法BigADjustUp：(大堆)向上調整算法

假設有一個數組，在邏輯上看做一顆完全二叉樹。我們通過從根節點開始的向上調整算法可以把它調整成一個大堆。

假設該數組為：

int a[] = { 17,15,28,22,13,5,9 };

可以看到該數組中的內容并不符合大堆要求。

向上調整算法核心思路：

①默認數組第一個元素為根節點數據；

②之后每Push進一個數據，便與它的父節點比較，若父節點數據小于子節點數據，則交換，然后將父節點(下標)賦值給子節點，再計算新父節點，重復上述步驟，直至子節點到根結點處（下標為0時）。

③中途若父節點數據大于等于子節點數據（滿足小堆要求），則break跳出循環。

代碼參考：

//大堆調整：
void BigADjustUp(Heap* hp, int loc)
{assert(hp);HPDataType* a = hp->_a;int child = loc;int parent = (child - 1) / 2;while (child > 0){if (a[parent] < a[child]){swap(&a[parent], &a[child]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}

解釋：

①父節點（parent）、子節點（child）在代碼中表示的是數組下標；

②loc，即location位置的意思，記錄Push數據在數組中的下標；

③計算新父節點：（左孩子或者右孩子的下標-1）/ 2就==他們父節點的下標，比如數組下標1與數組下標2的父節點在數組中就是下標0；

④每push進一個數據，先讓他做當前位置對應的左或者右孩子（該位置肯定是是葉節點），然后通過向上調整算法，若數據大于父節點中的數據，則交換、上升。

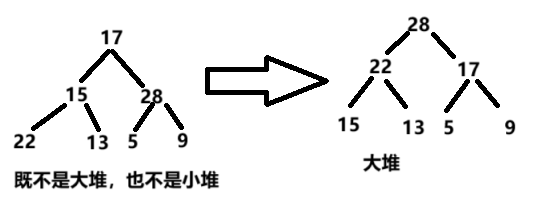
用該算法調整后：

int a[] = { 17，15，28，22，13，5，9 };

調整后：{28，22，17，15，13，5 ，9}；

HeapPopBig：刪除節點

將堆頂元素與數組最后一個元素交換，_size--，然后調用向下調整算法。

// 堆的刪除:為堆排序
void HeapPopBig(Heap* hp)
{assert(hp);assert(hp->_a);swap(&hp->_a[0], &hp->_a[hp->_size - 1]);hp->_size--;BigADjustDown(hp, 0);
}

將堆頂元素與最后一個元素交換位置后，重要的是調用BigADjustDown（）函數，使得堆能繼續成立。

核心算法BigADjustDown：向下調整算法

向下調整算法有一個前提：左右子樹必須是堆，才能調整。

堆的刪除，即刪除堆頂元素需要用到第二個核心算法——向下調整算法。

我們先說明堆刪除的思想：將堆頂元素與數組最后一個元素交換，然后_size--。

也就是說，向下調整算法的核心目標是：將堆頂所在的元素調整到適合它的位置。

算法思路：

①選擇該父節點對應的左/右孩子節中值較大的那一個，與父節點的值交換（一開始是根節點）；

②將交換的孩子節點當作新一輪的父節點，重復①；

③直到數組末尾，或者中途遇到小于或等于，滿足小堆條件退出。

void BigADjustDown(Heap* hp, int loc)
{assert(hp);HPDataType* a = hp->_a;//parent與child均為下標int parent = loc;int lchild = parent * 2 + 1, rchild = (parent + 1) * 2, max_child = 0;while (parent < hp->_size){max_child = a[lchild] > a[rchild] ? lchild : rchild;if (hp->_a[max_child] > hp->_a[parent] && max_child < hp->_size){swap(&hp->_a[parent], &hp->_a[max_child]);parent = max_child;lchild = parent * 2 + 1;rchild = (parent + 1) * 2;}else{break;}}}

解釋：

①新父節點下標：已知父節點的數組下標，那么該節點的左孩子數組下標=父節點下標*2+1，右孩子數組下標=（父節點下標+1）*2。如父節點數組下標為0，則左孩子為0*2+1，右孩子為（0+1)*2。

②BigADjustDown是配合HeapPopBig使用的，所以不要忘了實際場景是：堆頂與末尾數據進行了交換，需要BigADjustDown重新調整堆。

這也是為什么排升序要建大堆，排降序建小堆的原因：因為實現機制是將堆頂數據倒插到數組尾，大堆堆頂是數組數據最大的，故為升序；小堆堆頂是數組最小的，故為降序。

HeapDestory：堆的銷毀

記得將無用指針置空，防止野指針。

// 堆的銷毀
void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_capacity = hp->_size = 0;hp->_a = NULL;
}

2.堆排序代碼

//堆排序:升序
void HeapSortUp(int* a, int n)
{if (!a)return;Heap he;HeapCreateBig(&he, a, n);int cnt = n;while (cnt){HeapPopBig(&he);cnt--;}for (int i = 0; i < n; ++i)a[i] = he._a[i];HeapDestory(&he);
}

解釋：

①將傳入的數組通過HeapCreateBig構建起大堆；

②while循環，通過利用HeapPopBig每循環一次將堆頂（最大數據）移動至數組末尾，由于HeapPopBig一次成員變量_size便會--（數組尾下標不斷向前），當循環結束后成員變量數組_a存儲的數據便是升序排列；

這里利用HeapPopBig刪除機制，將堆頂逐漸移動至數組尾，但注意不是真正的刪除了而是堆中的_size--了（下次再向堆中push數據就會將原數據覆蓋），實際如果不再push那么這些數據是依然存在的。

③最后的for循環將排好的堆內數組挨個賦值給外部數組，之后再銷毀堆。

?以上述調整后：{28，22，17，15，13，5 ，9}的數組為例模仿代碼執行，

while中HeapPopBig執行情況：

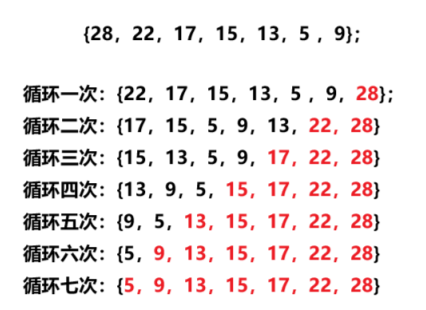
三、分析堆排序

特性總結：
1.同樣是選擇排序，相比直接選擇排序，堆排序使用堆來選數，效率高了很多。
2. 時間復雜度：建堆過程為O(n)，每次調整（彈出）為O(log n)，總共n次調整，所以整體時間復雜度為O(n log n)
3. 空間復雜度：本文中的代碼實現為O(N)（也可以采取另一種原地建堆的方法，那樣空間復雜度為O(1)）；
4. 穩定性：不穩定，交換堆頂和末尾元素時，可能破壞相同元素的相對順序。