算法	相關知識點	可以通過點擊	以下鏈接進行學習	一起加油！
斐波那契數列模型	路徑問題

多狀態問題通常涉及多個決策點和狀態轉換，解決起來復雜且計算量大。動態規劃作為一種強大的算法工具，能夠通過將問題分解為子問題并逐步求解，顯著提升解決這類問題的效率。本文將探討如何運用動態規劃技術有效處理復雜的多狀態問題，幫助讀者理解其背后的原理，并展示如何設計高效的狀態轉移方程以優化問題求解過程。

🌈個人主頁：是店小二呀
🌈C/C++專欄：C語言\ C++
🌈初/高階數據結構專欄： 初階數據結構\ 高階數據結構
🌈Linux專欄： Linux
🌈算法專欄：算法
🌈Mysql專欄:Mysql

🌈你可知:無人扶我青云志 我自踏雪至山巔

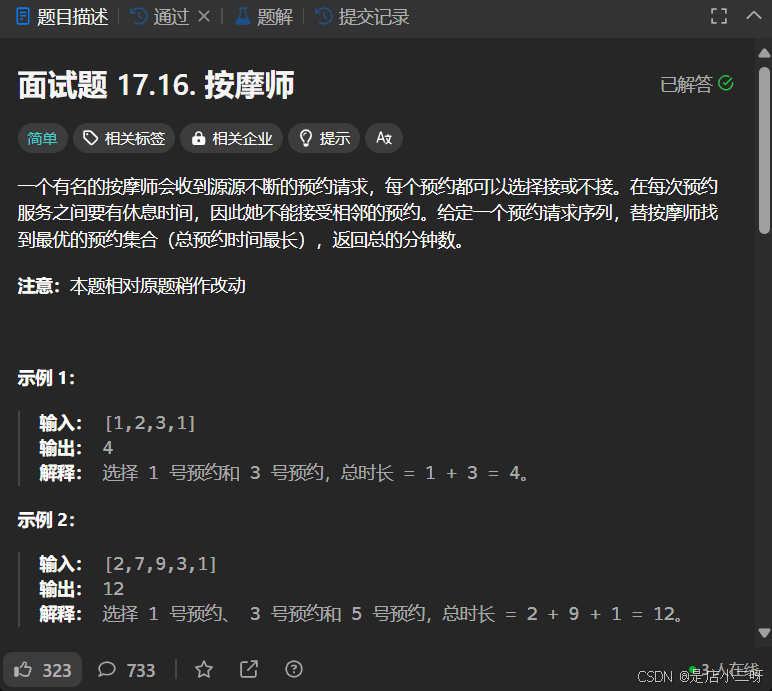
面試題 17.16. 按摩師

【題目】：面試題 17.16. 按摩師

【算法思路】

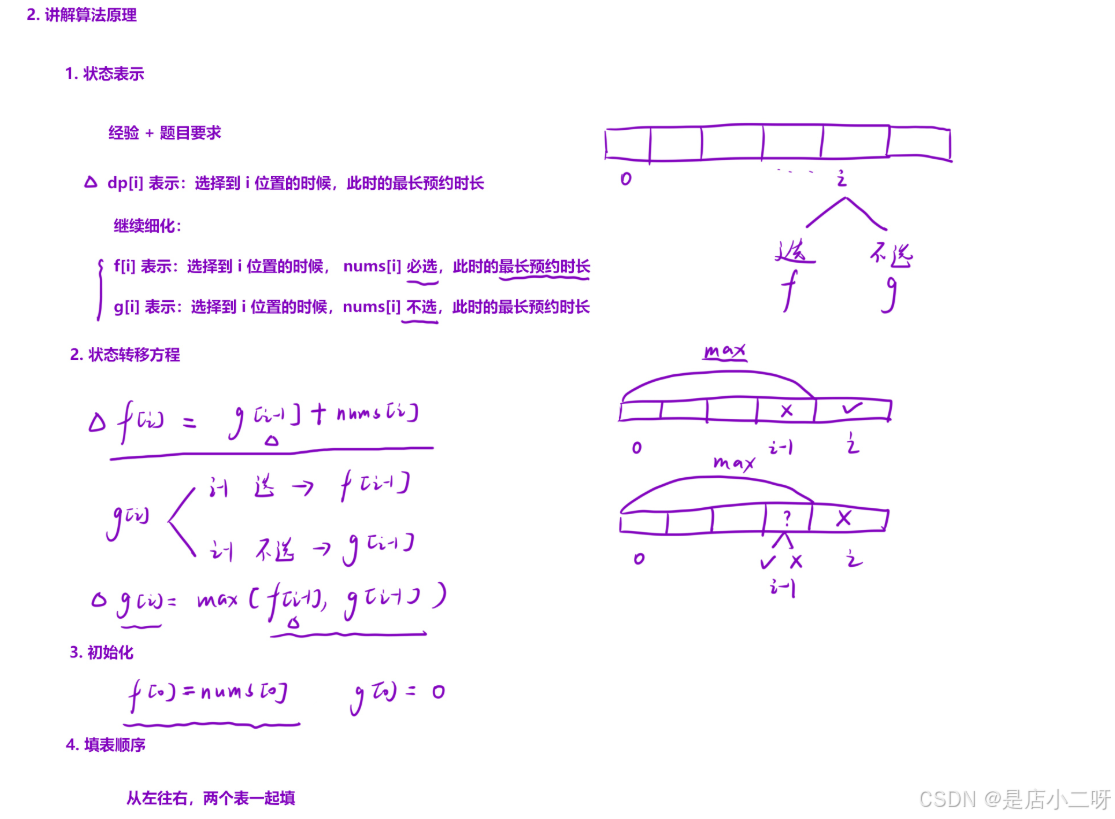
通過題目分析，狀態可以表示為選擇到第 i 位置時的最長預約時長。進一步細化后，題目提供了兩種狀態：是否選擇 nums[i]，這會影響最終結果。為此，我們可以創建兩個 DP 表，分別表示選擇或不選擇 nums[i] 的情況，并根據不同狀態進行處理。

題目要求不能連續選擇，因此我們需要根據狀態的定義以及與前一個狀態之間的關系，推導出狀態轉移方程。對于不選擇 nums[i] 的情況，上一狀態的選擇與否都會影響當前的最長預約時長，這與具體的選擇策略密切相關

解決問題的關鍵在于，通過在第 i 位置引入多種狀態，利用動態規劃（DP）來求解。結合題目需求，我們需要確保DP表之間的狀態連續性，從而推導出合理的狀態轉移方程。

【代碼實現】

class Solution {
public:int massage(vector<int>& nums) {int n = nums.size();if(n == 0) return 0;///1.為多狀態創建dp表vector<int> f(n);vector<int> g(n);//2.初始化f[0] = nums[0];//3.填表for(int i = 1; i < n; i++){f[i] = g[i - 1] + nums[i];g[i] = max(f[i - 1], g[i - 1]);}//4.返回值return max(f[n - 1],g[n - 1]);}
};

---

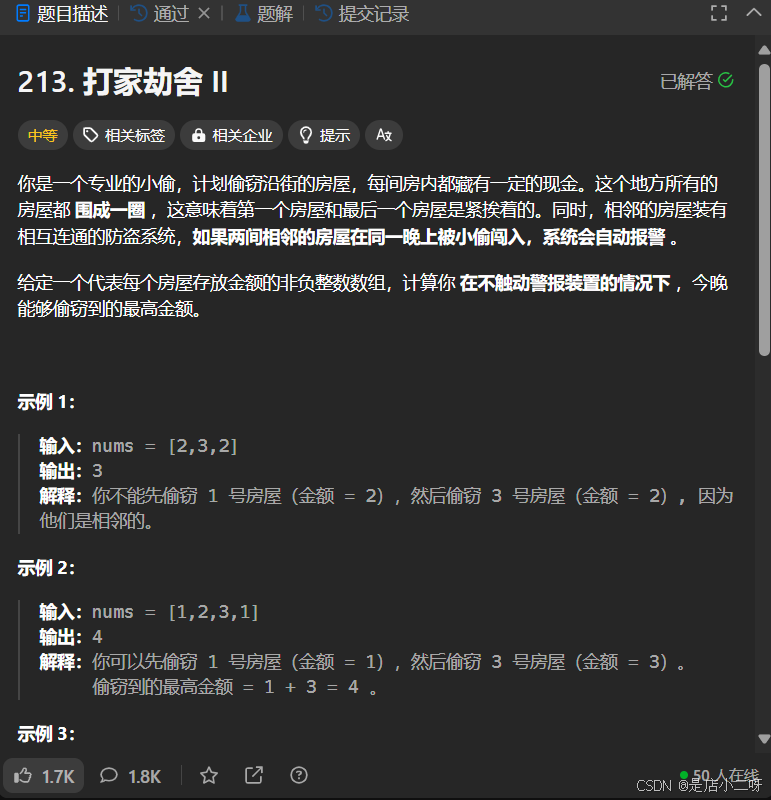
213. 打家劫舍 II

【題目】：213. 打家劫舍 II

【算法思路】

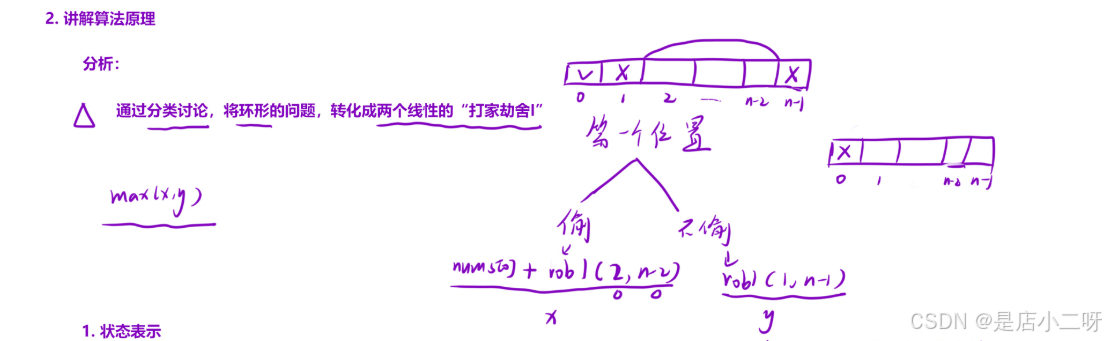
繪圖分析是一種快速的問題分析方法。通過畫圖分析，我們可以根據第一個位置是否選擇，分成兩個部分。剩余部分的處理方式與“面試題 17.16. 按摩師”的解法類似，使用簡單的多狀態動態規劃（DP）方法即可解決。

在解決問題的過程中，可以根據一些特殊條件將問題劃分為子問題，從而使用相同的邏輯來處理這些子問題，這樣有助于簡化并有效解決其中可能存在的特殊情況。

【代碼實現】

class Solution {
public:int rob(vector<int>& nums) {   int n = nums.size();int ret =max ( nums[0] + rob1(nums, 2, n - 2), rob1(nums,1, n - 1));return ret;}int rob1(vector<int>& nums, int left, int rigth){if(left > rigth) return 0;//1.創建db表int n = nums.size();vector<int> f(n);auto g = f;//2.初始化f[left] = nums[left];//3.填表for(int i = left + 1; i <= rigth; i++){f[i] = g[i - 1] + nums[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[rigth],g[rigth]);}
};

---

740. 刪除并獲得點數

【題目】：740. 刪除并獲得點數

【算法思路】

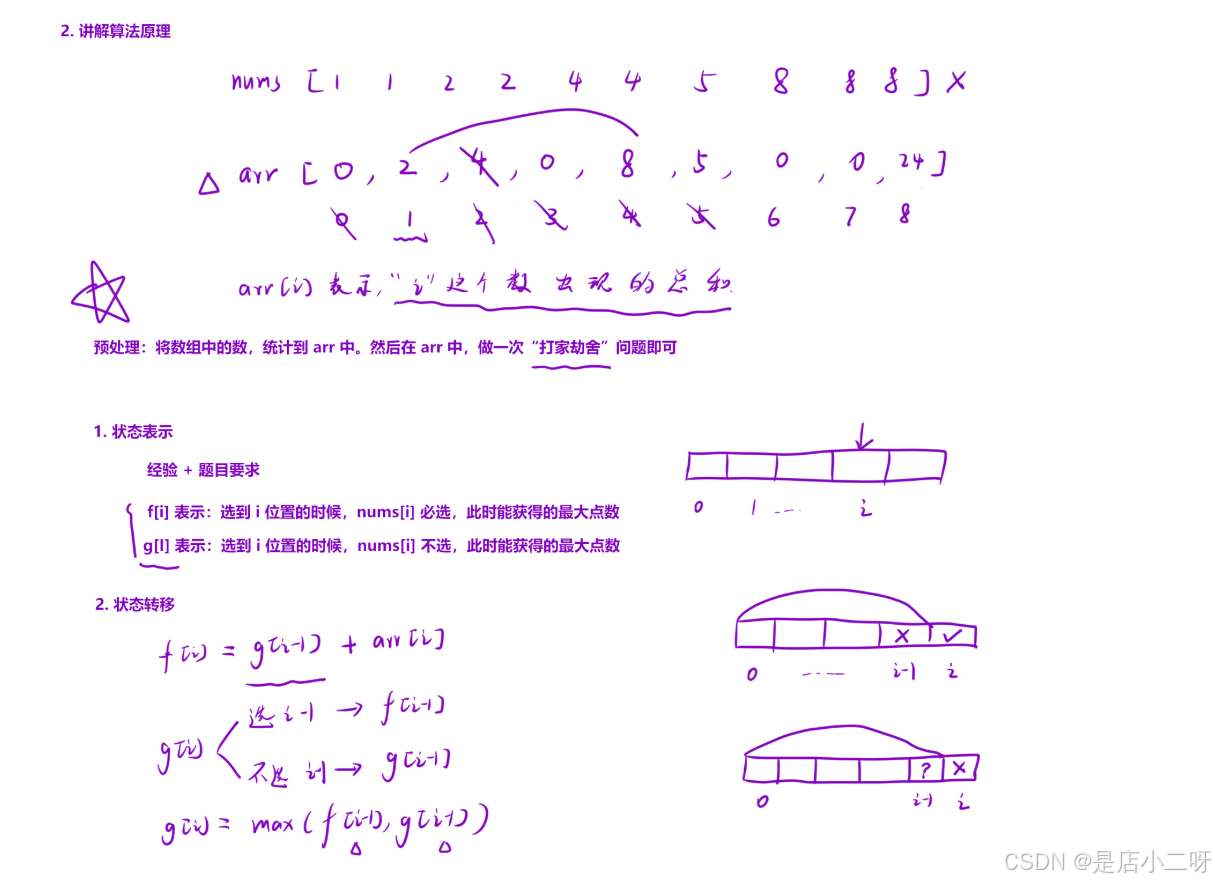
有些題目可能需要預處理，才能更容易發現使用動態規劃（DP）來解決問題。例如，在這道題中，直接從題目入手使用DP并不可取。我們需要刪除 nums[i] - 1 和 nums[i] + 1 這些元素，換句話說，要跳過這些無法相加的元素。

同時，題目要求獲取最大值，通常在這種情況下，若需要快速查找元素，需要連續下標訪問，哈希表是一個常見的選擇。但在這里，我們只需要根據數組下標來查找元素，元素代表相加點數，數值為下標方便操作，因此可以用數組的下標值作為哈希表的替代，通過這種方式進行DP操作更加簡便。

【代碼實現】

class Solution {
public:int deleteAndEarn(vector<int>& nums) {//1.預處理const int N = 10001;int arr[N] = {0};for(auto x : nums) arr[x] += x;//2.創建dp表vector<int> f(N);auto g = f;//3.填表操作for(int i = 1; i < N; i++){f[i] = g[i - 1] + arr[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[N - 1], g[N - 1]);}
};

---

LCR 091. 粉刷房子

【題目】：LCR 091. 粉刷房子

【算法思路】

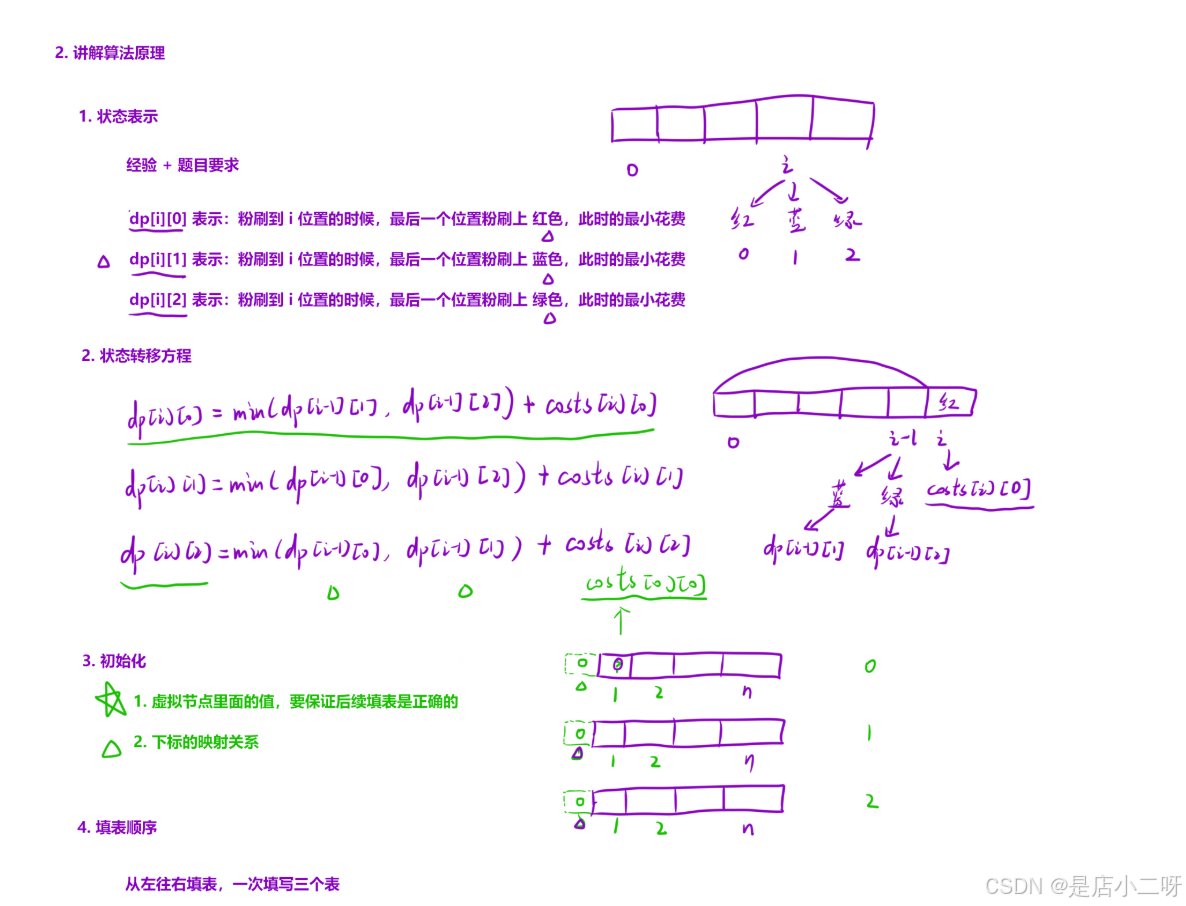
屬于很典型的簡單多狀態dp問題，在i位置時候，通過選擇顏色，此時的最小花費。dp細分為三種顏色，在該i位置的最小花費，然后跟最近一次狀態，寫出狀態轉移方程。三個狀態表示相互作用，相互呼應，最后判斷最小就行了。這里建議搞個虛擬節點。

【代碼分析】

我們可以搭建一個二維數組，其中每個元素代表一個分化的DP表，用來記錄在第 i 位置選擇某種顏色時的最小花費。

根據分析出的狀態轉移方程，可以通過另外兩個DP表獲取前兩個狀態的最小值，并加上當前顏色的花費，從而計算出當前狀態的最小花費。可以將這兩個二維數組視作疊加在一起，三個DP表根據狀態轉移方程共同處理問題，通過這種方式有效地求解最小花費。

感覺面向過程有點難，不如選擇面向對象編程，對于這些問題的處理。

【虛擬節點】

虛擬節點需要保證后續填表正確性，那么可以圖像結合狀態轉移方程，決定虛擬節點初始化數值。

【代碼實現】

class Solution {
public:int minCost(vector<vector<int>>& costs) {int n = costs.size();//1.多狀態 創建dp表vector<vector<int>> dp(n + 1,vector<int>(3));//2.初始化操作dp[0][0] = dp[0][1] = dp[0][2] = 0;for(int i = 1; i <= n; i++){dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0];dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1];dp[i][2] = min(dp[i - 1][1], dp[i - 1][0]) + costs[i - 1][2]; }return min(dp[n][1], min(dp[n][2], dp[n][0]));}
};

---

309. 買賣股票的最佳時機含冷凍期

【題目】：309. 買賣股票的最佳時機含冷凍期

【算法思路】

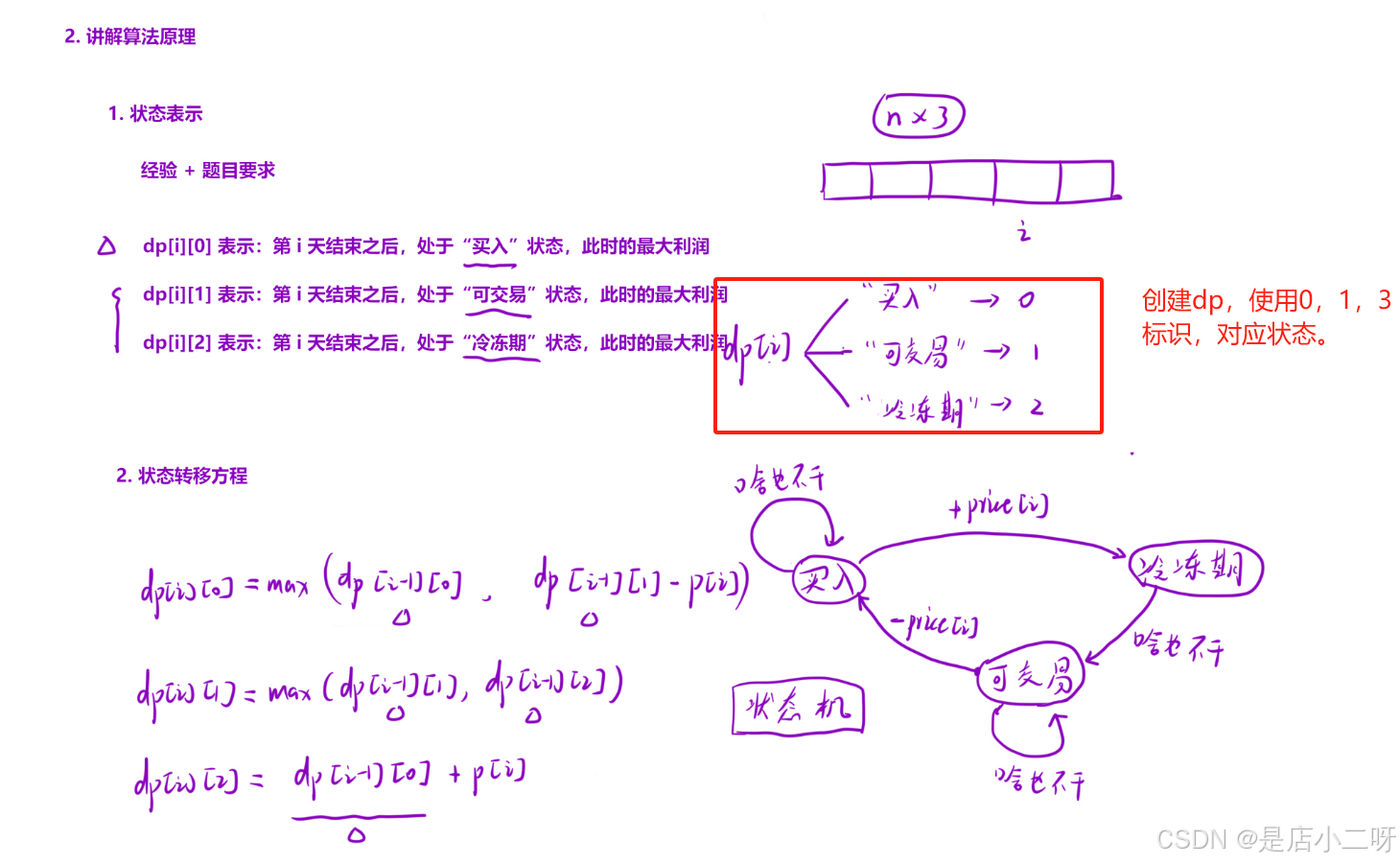
結合上道題經驗，遇到狀態超過兩種，可以使用0，1，2標識不同狀態標識，dp[i] [0]、dp[i] [1]、dp[i] [2]表示i位置，巴拉巴拉狀態。

常用手段是畫出"狀態機"分析狀態之間轉化，方便寫出動態轉移方程和初始化處理。這里選擇以為i位置結束，所表示狀態。根據狀態機某個位置，結合最近一次位置結合題目分析，寫出然后得到當前位置數值，從而得到狀態轉移方程。

【代碼實現】

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();//1.創建多狀態dp表vector<vector<int>> dp(n, vector<int>(3));//2.初始化dp[0][0] = -prices[0];dp[0][1] = dp[0][2] = 0;//3.填表for(int i = 1; i < n; i++){dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);dp[i][2] = dp[i - 1][0] + prices[i];}return max(dp[n - 1][1], max(dp[n - 1][2], dp[n - 1][0]));}
};

---

714.買賣股票的最佳時機含手續費

【題目】：714. 買賣股票的最佳時機含手續費

【算法思路】

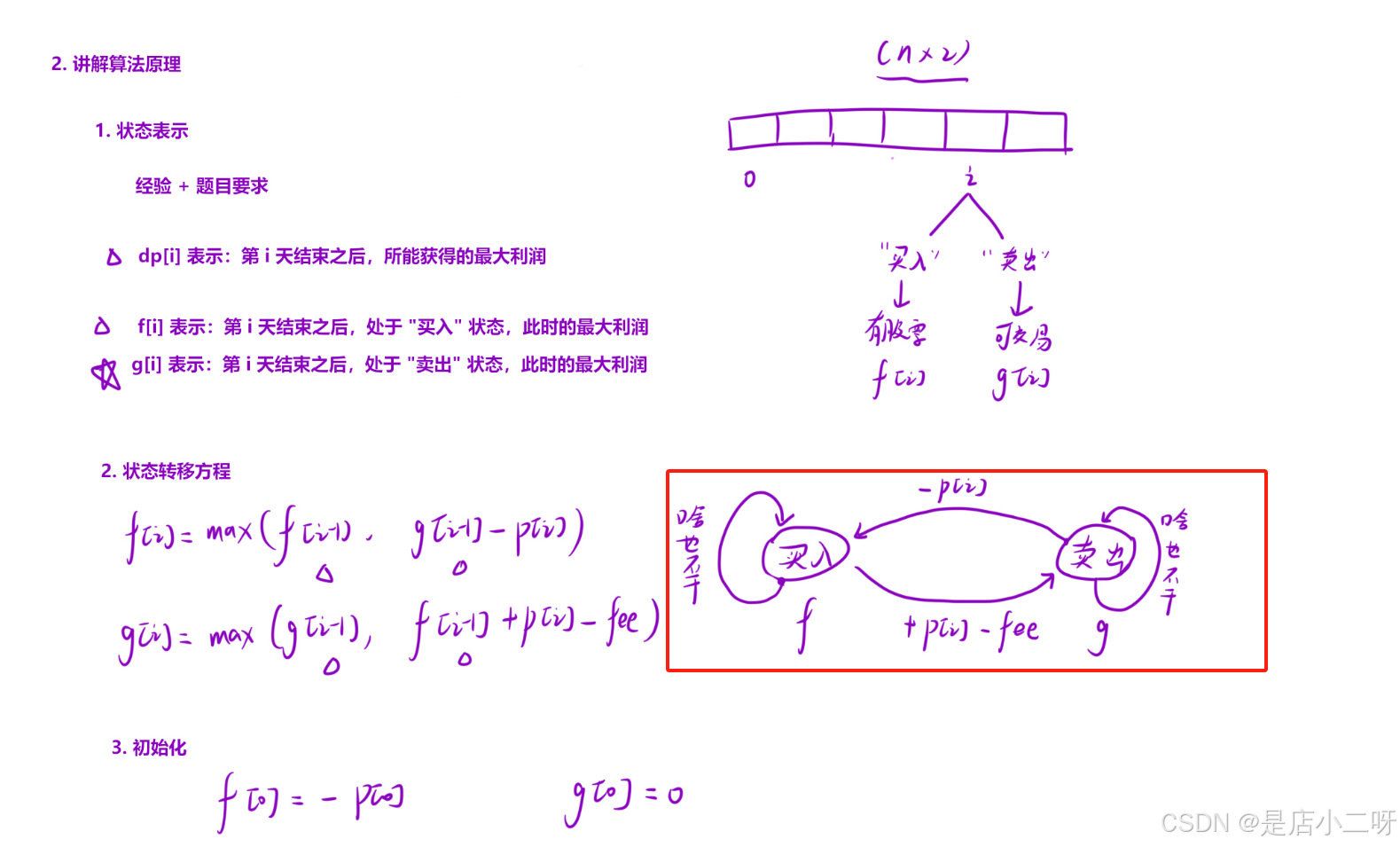
首先，根據經驗和題目要求，得出狀態轉移方程。然后選擇合適的i位置進行狀態分析，得到買入狀態和可交易狀態的表示。

接下來，可以通過關聯最近一次的位置來確定狀態轉移方程，或者繪制狀態機圖，將所有狀態轉化過程進行分析。最后，初始化相關位置，通過狀態轉移方程確定初始位置，并在圖中進行分析。

【代碼實現】

class Solution {
public:int maxProfit(vector<int>& prices, int fee) {//1.創建dp表int n = prices.size();vector<int> f(n);auto g = f;//2.初始化f[0] = -prices[0];g[0] = 0;//3.填表操作for(int i = 1; i < n; i++){f[i] = max(f[i - 1], g[i - 1] - prices[i]);g[i] = max(g[i - 1], f[i - 1] + prices[i] - fee);}return g[n- 1];}
};

---

123. 買賣股票的最佳時機 III

【題目】：123. 買賣股票的最佳時機 III

【算法思路】

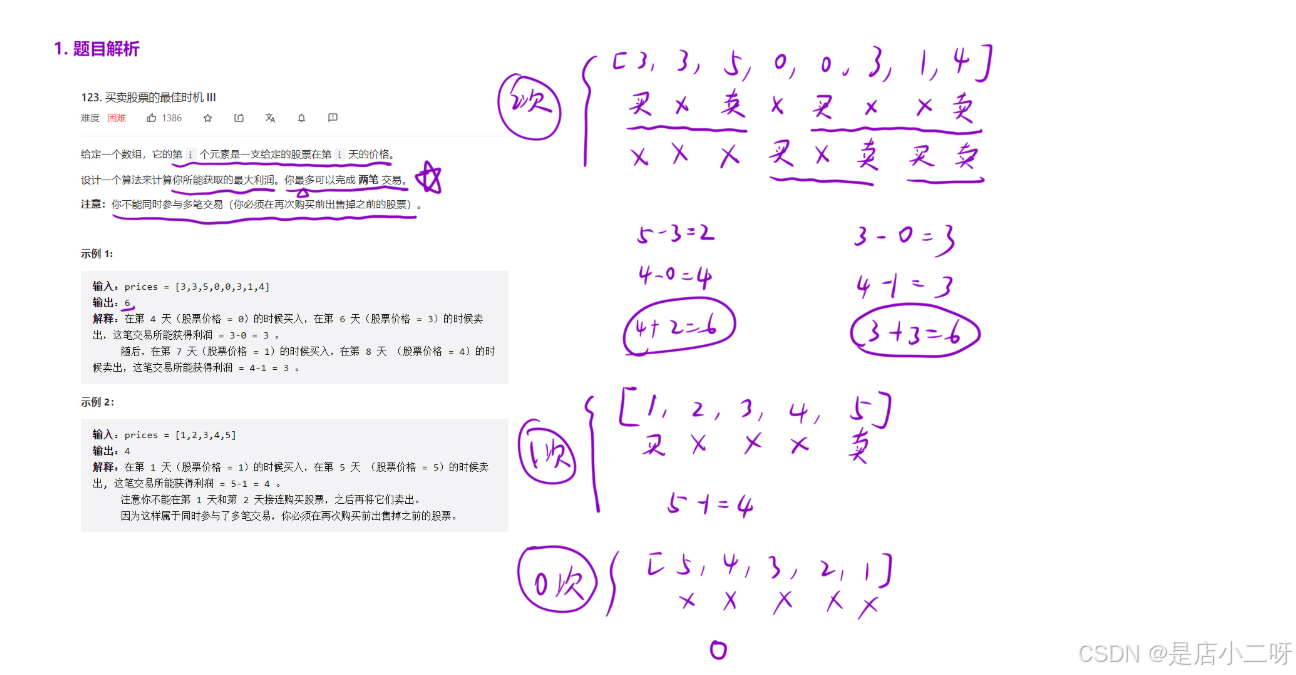
在解決問題之前，我們需要結合題目和樣例進行繪圖模擬，直觀地展示整個過程。在這里，'最多’的含義是指從0到最大范圍，而并非一定要選擇這么多。

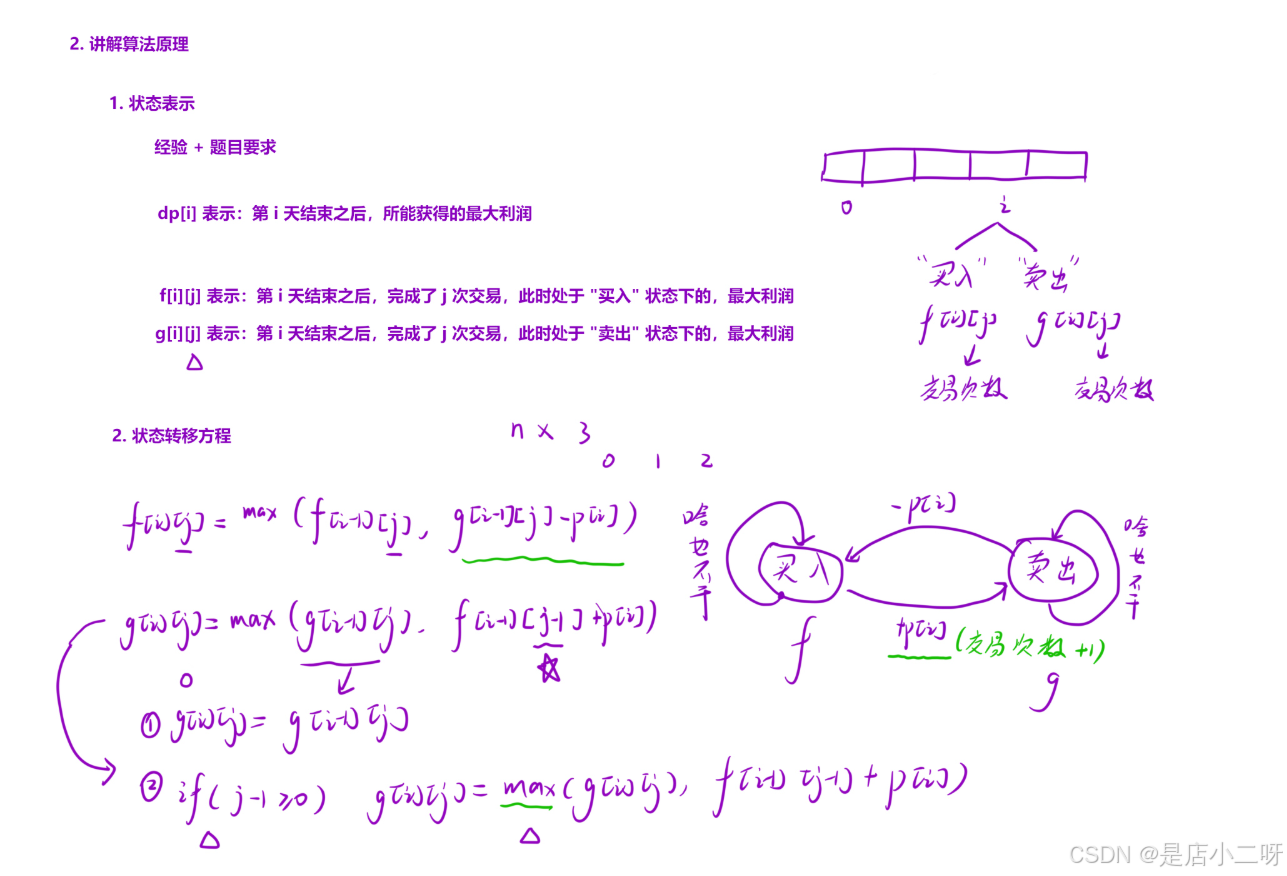
首先，根據’經驗 + 題目要求’得到初步的狀態表示，并通過 i 位置進行分析。如果發現該狀態表示不夠充分，可以增加一個位置來表示’完成了多少次交易’。

接下來，繪制狀態機并推導出狀態轉移方程。在處理狀態轉移方程時，需考慮所有細節。例如，題目中的狀態轉移方程可能會涉及越界問題，需在初始化過程中解決這個隱含問題。

特別需要注意的是，第一行位置的初始化應為[1, n - 1]并設置為無窮小，以避免不必要的干擾。此外，初始化某些位置時，要確保它們不會影響后續位置的正確計算，或者確保后續位置能夠正確更新。

【代碼實現】

class Solution {
public:const int INT = -0x3f3f3f3f;int maxProfit(vector<int>& prices) {//1.創建dp表int n = prices.size();vector<vector<int>> f(n, vector<int>(3,INT));auto g = f;//2.初始化f[0][0] = -prices[0];g[0][0] = 0;//3.填表操作for(int i = 1; i < n; i++){for(int j = 0; j < 3; j++){f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);g[i][j] = j - 1 >= 0 ? max(g[i - 1][j], f[i - 1][j - 1] + prices[i]) : g[i - 1][j];}}int ret = 0;for(int j = 0; j < 3; j++)ret = max(ret, g[n - 1][j]);return ret;}
};

---

188. 買賣股票的最佳時機 IV

【題目】：188. 買賣股票的最佳時機 IV

【算法思路】

首先處理 k 的值，考慮到 k 可能超過所需的總天數，通過數學方法將 k 調整到一個合理范圍內。

這道題算法思路同上道題一樣，主要畫出"狀態機"分析狀態轉移方程，同時需要分析狀態轉移方程出現的問題。

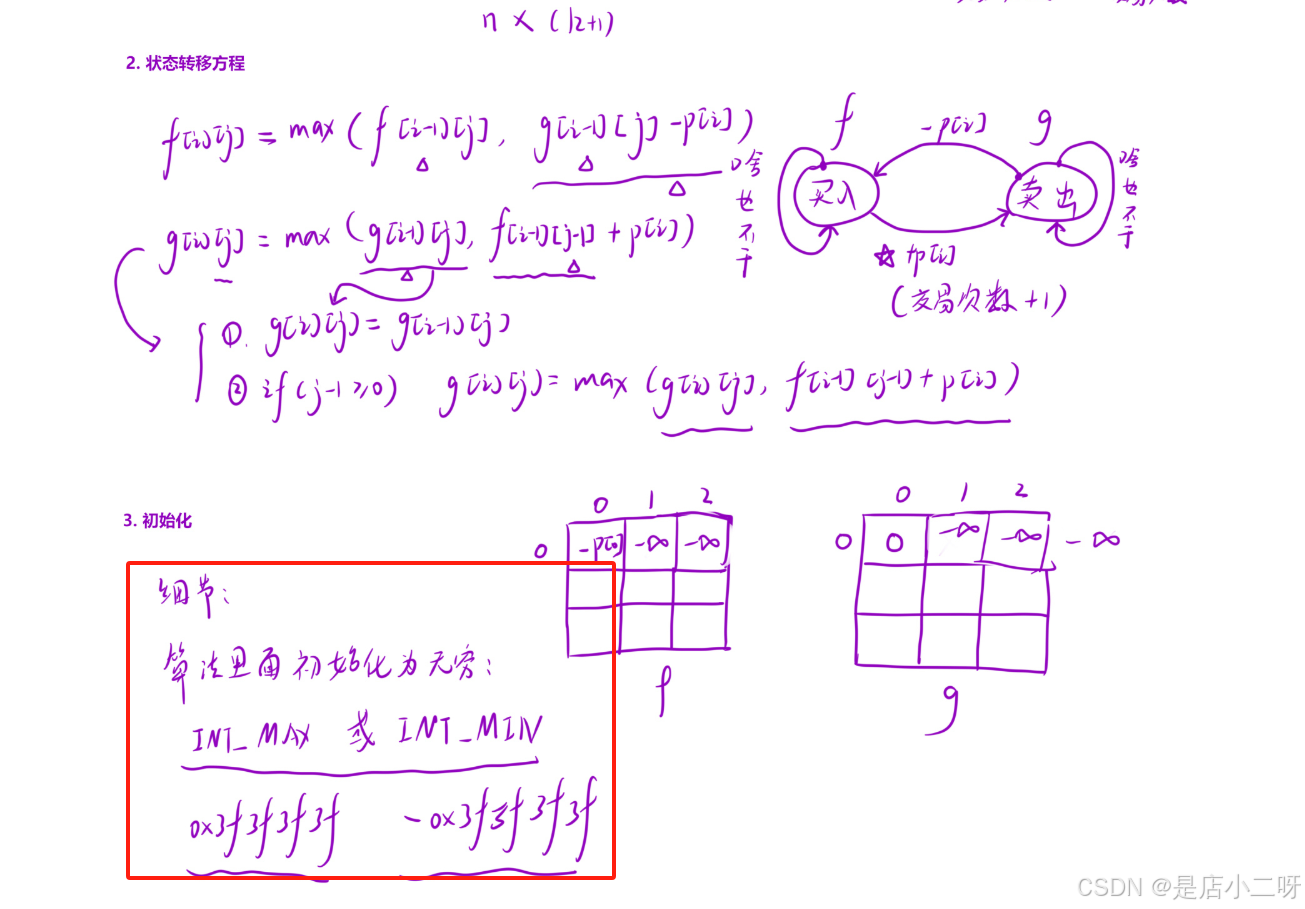
【代碼實現】

class Solution {
public:const int INF = -0x3f3f3f3f;int maxProfit(int k, vector<int>& prices) {     int n = prices.size();       k = min(k, n/2);//1.創建dp表      vector<vector<int>> f(n, vector<int>(k + 1, INF));auto g = f;//2.初始化f[0][0] = -prices[0];g[0][0] = 0;//3.填表操作for(int i = 1; i < n; i++){for(int j = 0; j <= k; j++){f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if(j - 1 >= 0)g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);}}int ret = 0;for(int j = 0; j <= k; j++) ret = max(ret, g[n - 1][j]);return ret;}
};

快和小二一起踏上精彩的算法之旅！關注我，我們將一起破解算法奧秘，探索更多實用且有趣的知識，開啟屬于你的編程冒險！