網址：主站

工具補充

1. sort 函數的使用規則

• 作用：對容器元素進行排序，默認升序。
• 語法：sort(起始迭代器, 結束迭代器, 比較規則)
  • 前兩個參數是排序范圍：[begin, end)（包含begin，不包含end）。
  • 第三個參數可選：自定義比較規則（默認用 < 比較，即升序）。
• 代碼場景：
  sort(jobs.begin(), jobs.end(), [](const vector<int>& a, const vector<int>& b) { return a[1] < b[1]; })
  表示按 jobs 中每個子數組的第二個元素（結束時間）升序排序。
  • 為什么用 <？因為比較規則返回 true 時，a 會排在 b 前面。a[1] < b[1] 意味著“結束時間小的 job 排在前面”，即升序。

2. begin() 和 end() 迭代器

• 迭代器：可理解為“容器元素的指針”，用于訪問容器元素。
• begin()：返回指向容器第一個元素的迭代器。
• end()：返回指向容器最后一個元素之后的迭代器（標記范圍終點，不指向實際元素）。
• 用途：搭配算法（如 sort）指定操作范圍，形成 [begin, end) 左閉右開區間，確保遍歷/排序不越界。

3. Lambda 表達式（匿名函數）

• 格式：[捕獲列表](參數列表) { 函數體 }
  此處 [] 表示無捕獲，(const vector<int>& a, const vector<int>& b) 是參數，{ return a[1] < b[1]; } 是函數體。
• 作用：臨時定義短小的函數，作為 sort 等算法的自定義比較規則。
• 代碼場景：告訴 sort 如何比較兩個 job——用它們的結束時間（a[1] 和 b[1]）比較，實現按結束時間排序。

4. rbegin() 反向迭代器

• 作用：返回容器的反向起始迭代器，指向容器最后一個元素（與 begin() 方向相反）。
• 代碼場景：dp.rbegin() 指向 map 中鍵最大的元素（因為 map 按鍵升序排列，最后一個元素鍵最大）。
  dp.rbegin()->second 即獲取當前最大時間對應的最大利潤（不選擇當前工作時的最大利潤）。

5. ->second 訪問 map 的值

• map 存儲的是鍵值對（pair<key, value>），迭代器指向 pair 對象。
• ->first：訪問鍵（key）；->second：訪問值（value）。
• 代碼場景：dp 中鍵是時間，值是該時間的最大利潤。prev(...)->second 即獲取“開始時間前的最大利潤”。

6. prev() 函數

• 作用：返回迭代器的前一個位置（即 --iterator 的結果），需迭代器支持 -- 操作（如 map 的迭代器）。
• 代碼場景：prev(dp.upper_bound(begin)) 用于獲取“最后一個鍵 <= begin 的元素迭代器”（配合 upper_bound 查找）。

7. 二分相關庫函數匯總

核心邏輯關聯

代碼通過 sort 按結束時間排序 jobs，用 map 存儲“時間-最大利潤”映射，借助 upper_bound+prev 快速找到不沖突的歷史最大利潤，用 rbegin 獲取當前最大利潤，最終通過動態規劃選擇最優解。這些工具共同實現了高效的時間復雜度（O(nlogn)）。

排序算法

排序關鍵指標：

1. 時空復雜度；
2. 排序穩定性：
   • 排序后相對位置沒有發生改變，單單排int類型意義不大，但是對于復雜的數據，比如訂單數據，有訂購時間和用戶id，那如果是穩定排序，排序后相同用戶id依然會按照交易日期有序排列；
   • 如果用不穩定排序，相同用戶id的訂單相對位置可能變化，
3. 是否原地排序：是否不需要額外的輔助空間，只需要常數級別額外空間？能否最直接操作原數組？

1. 選擇排序【不穩定】

• 遍歷一遍數組，找到最小值
• 與數組第一個元素交換
• 接著從第二個開始重復以上操作

void sort(vector<int>& nums) {int n = nums.size();// sortedIndex 是一個分割線// 索引 < sortedIndex 的元素都是已排序的// 索引 >= sortedIndex 的元素都是未排序的// 初始化為 0，表示整個數組都是未排序的int sortedIndex = 0;while (sortedIndex < n) {// 找到未排序部分 [sortedIndex, n) 中的最小值int minIndex = sortedIndex;for (int i = sortedIndex + 1; i < n; i++) {if (nums[i] < nums[minIndex]) {minIndex = i;}}// 交換最小值和 sortedIndex 處的元素int tmp = nums[sortedIndex];nums[sortedIndex] = nums[minIndex];nums[minIndex] = tmp;// sortedIndex 后移一位sortedIndex++;}
}

• 空間復雜度是 O(1)，是個原地排序。
• 時間復雜度 $O(n^2)$，嵌套for循環
• 數組本來有序性對算法執行次數的影響：無影響，即便原本有序，也會執行$O(n^2)$
• 非穩定排序：交換操作使排序失去了穩定性，無法維持原來相等元素的相對位置。

2. 冒泡排序【擁有穩定性】

選擇排序三大問題：

• 不穩定，交換導致改變相同元素相對位置
• 時間復雜度與初始有序度無關，即便一開始是完全有序，時間復雜度還是$O(n^2)$
• 執行次數大概是$(n^2)/2$，無法優化

1. 優化穩定性

選擇排序將最小值交換到最前面，

• 最小值放到前面這一步本身不會破壞穩定性，

• 將最前面的值放到最小值的位置，自然就破壞了最前面值原本的穩定性。

• 所以，我們還是將最小值放到最前面，但是最前面的值不再直接放到最小值位置，而是整體向后移動。

// 對選擇排序進行第一波優化，獲得了穩定性
void sort(vector<int>& nums) {int n = nums.size();int sortedIndex = 0;while (sortedIndex < n) {// 在未排序部分中找到最小值 nums[minIndex]int minIndex = sortedIndex;for (int i = sortedIndex + 1; i < n; i++) {if (nums[i] < nums[minIndex]) {minIndex = i;}}// 優化：將 nums[minIndex] 插入到 nums[sortedIndex] 的位置// 將 nums[sortedIndex..minIndex] 的元素整體向后移動一位int minVal = nums[minIndex];// 數組搬移數據的操作for (int i = minIndex; i > sortedIndex; i--) {nums[i] = nums[i - 1];}nums[sortedIndex] = minVal;sortedIndex++;}
}

獲得了穩定性，但是執行效率降低了，因為變成了雙層for循環外加一次for循環，執行次數遠大于$n^2/2$。

第一次雙層for循環找到最小值
第二次for循環將最小值插入，并且整體后移

2. 優化時間復雜度
繼續優化時間復雜度，合并上面兩次for循環，實現了冒泡排序的本質：倒序遍歷n次，每次都邊找最小值邊排序，即交換逆序對

• n次倒序遍歷nums[sortedIndex…]
• 如果發現了逆序對就交換順序
• 這樣nums[sortedIndex…]的最小值就是慢慢移動到nums[sortedIndex]
• 全程只交換相鄰逆序對，完全不動相同元素，所以穩定排序。
• 冒泡排序，從尾部向頭部冒泡

void sortVector<vector<int>& nums> {int n = nums.size();// sortedIndex前面都是有序的int sortedIndex = 0;	// n次遍歷！每次把當前最小的值pop到最前面也就是sortedIndex = 0位置while (sortedIndex = 0) {  for (int i = n - 1; i > sortedIndex; i-- ) {// 如果發現一次逆序對(前>后)就交換if (nums[i - 1] > nums[i]) {// swap交換逆序對int tmp = nums[i];nums[i] = nums[i-1];nums[i-1] = tmp;}}// 成功把最小值pop到前面一次sortedIndex++; 										}
}

這個算法的名字叫做冒泡排序，因為它的執行過程就像從數組尾部向頭部冒出水泡，每次都會將最小值頂到正確的位置。

3. 提前終止
還有個優化點，那就是選擇排序和目前的冒泡排序都是與數組原始有序性無關的，即便已經有序，也會執行$O(n^2)$次，我們可以想辦法檢測有序性提前終止程序。
flag編程：用這個標記編程的思想，如果某次倒序遍歷完全沒有找到逆序對，沒有發生swap，則說明已經有序，不需要繼續執行程序！
只需要加一個bool值，記錄每次倒序遍歷是否發生swap即可！

void sortVector<vector<int>& nums> {int n = nums.size();int sortedIndex = 0;	while (sortedIndex = 0) {  // 設置flag, 初始化沒有發生swapbool swapped = false; for (int i = n - 1; i > sortedIndex; i-- ) {if (nums[i - 1] > nums[i]) {int tmp = nums[i];nums[i] = nums[i-1];nums[i-1] = tmp;// 如果發生了swap，設為truebool swapped = true;}}// 如果某次遍歷完全沒有swap,說明已經有序，退出程序if (!swapped) break; sortedIndex++; 										}
}

3. 插入排序【逆向思維】【撲克牌抓牌】

對選擇排序不穩定的問題，我們有一些解決辦法了：

• 保住穩定性：我們提出了一次for循環找到最小值，最小值放在最前面，然后再一次for循環把其他元素都逐一往后排，保住了排序的穩定性；
• 冒泡排序：倒序遍歷 + 交換逆序對 + flag編程提前終止
• 成功合并了for循環，還有其他方法把while里面的兩個for優化成一個for循環么？

逆向思維：

• 前面兩種算法都是在后面 nums[sortedIndex…] 中找到最小值，然后將其插入到 前面nums[sortedIndex] 的位置，這兩步操作就是兩次for循環。
• 反過來想，能不能在nums[0…sortedIndex-1] 這個部分有序的數組中，找到 nums[sortedIndex] 應該插入的位置，然后進行插入呢？
  • 有序數組 nums[0…sortedIndex-1] 找到應該插入的位置，很自然想到用二分查找，這樣就可以把第一次for循環$O(n)$優化為$O(log(n))$
  • 但是找到后還得交換，又是一次for循環
  • 還不如繼續用冒泡的思想，一邊找一邊換？

// 對選擇排序進一步優化，向左側有序數組中插入元素
// 這個算法有另一個名字，叫做插入排序
void sort(vector<int>& nums) {int n = nums.size();// 維護 [0, sortedIndex) 是有序數組int sortedIndex = 0;while (sortedIndex < n) { // 將 nums[sortedIndex] 插入到有序數組 [0, sortedIndex) 中// 依舊是倒序遍歷，交換逆序對！for (int i = sortedIndex; i > 0; i++) {if (nums[i] < nums[i-1]) {int tmp = nums[i];nums[i] = nums[i-1];nums[i-1] = tmp;} else { // 到了該到的位置了！換不下去了！break;}}sortedIndex++;}

插入排序就像是打撲克，把新抓到的牌放到已經排好序的牌中：

1. 原地排序算法：空間復雜度
2. 時間復雜度依舊是$O(n^2)$，實際操作次數大約是$n^2/2$次
3. 穩定排序：只有在 nums[i] < nums[i - 1] 的情況下才會交換元素，所以相同元素的相對位置不會發生改變。
4. 與初始有序度強相關：
   • 初始有序度高，僅有個別元素逆序，則內層負責swap的for循環幾乎不操作，時間復雜度接近$O(n)$；
   • 初始完全逆序，插入排序效率極低，每次都與nums[0…sortedIndex-1] 所有元素交換，總時間復雜度極為接近$O(n^2)$。
   • 插入排序的實際操作次數會小于冒泡排序的

4.

理解h有序數組：

• 間隔h位置，是有序的數組

希爾排序是基于選擇排序進行優化的

• 插入排序的問題：上來就想一步到位，直接把亂序數組變成1有序數組
• 希爾的概念是不著急，先變成16有序數組，然后8有序數組，4，2，最后變成1有序數組，完成排序！

插入排序三步改動實現希爾排序：見代碼

// 希爾排序本質：對h有序數組進行插入排序
// 逐步縮小h
void sort(vector<int>& nums) {int n = nums.size();// 設置生成函數 2^(k-1)// 即 h = 1，2，3，4，...int h = 1;while (h < n/2) {	// h放到最大h = 2 * h;}// 改動一：插入排序所有邏輯套在h的while循環中while (h >= 1) {// 改動二：sortedIndex 初始值設置為 h ，而不是1int sortedIndex = h;while (sortedIndex < n) {// 改動三：把比較和交換元素的步長設置為h，而不是相鄰元素 // 依舊是倒序遍歷，交換逆序對（相隔h）！// 原來是： for (int i = sortedIndex; i > 0; i--) {for (int i = sortedIndex; i >= h; i-=h) {if (nums[i] < nums[i-h]) { // 減1都換成減hint tmp = nums[i];nums[i] = nums[i-h];nums[i-h] = tmp;} else { // 到了該到的位置了！換不下去了！break;}}sortedIndex++;}// 按照遞增函數的規則，縮小hh /= 2;}
}

• 時間復雜度終于低于$O(n^2)$
• 原地排序：空間復雜度 $O(1)$
• 不穩定排序，打亂了相同元素的順序！

5. 快速排序【妙用二叉樹前序位置】

6.

7.

8.

9.

10.

數據結構

鏈表題

數組題

雙指針

滑窗

二分搜索基本框架

思路很簡單，細節是魔鬼！
整型溢出在二分查找里面都不算事；
到底是給mid加一還是減一？
while 里面到底是 <= 還是 <?
要是沒有正確理解細節，二分對我來說就是玄學算法！

二分查找問題常見的三個場景：

• 尋找一個數；
• 尋找左側邊界；
• 尋找右側邊界；
  并且深入細節：
• while 里面 是否要帶等號？
• mid 是否 應該 +1？

計算 mid 需要防止溢出：

• left + (right - left) / 2
• 結果 其實與 (left + right) / 2 結果相同，但是有效防止了left right太大導致相加溢出的情況

二分查找的一個技巧：

• 不用else
• 把所有情況的else if 寫清楚，展示所有細節

int binarySearch(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (...) {int mid = left + (right - left) / 2;if (nums[mid] == target) {...} else if (nums[mid] < target) {left = ...} else if (nums[mid] > target) {right = ...}}
}

… 里面就是關鍵

尋找一個數字——最基本二分搜索

標準的二分搜索框架，搜索目標元素的索引，若不存在則返回 -1

class Solution {
public:// 標準的二分搜索框架，搜索目標元素的索引，若不存在則返回 -1int search(vector<int>& nums, int target) {int left = 0;// 注意int right = nums.size() - 1;while(left <= right) {int mid = left + (right - left) / 2;if(nums[mid] == target) {return mid;   } else if (nums[mid] < target) {// 注意left = mid + 1;} else if (nums[mid] > target) {// 注意right = mid - 1;}}return -1;}
};

細節一：為什么while循環的條件是 <= 而不是 < ？

• 因為初始化右指針right時，賦值是 n - 1，是最后一個元素索引，而不是 n；
• 搜索區間被定義為了一個閉區間 [left, right] ，而不是 [left, right) 左閉右開；
• 那寫成閉區間搜索，何時停止搜索呢?
  • 能找到target的情況，當然就是 nums[mid] == target時；
  • 找不到target的情況，就需要搜索區間 [left, right] 為空的時候停止搜索，注意 [left, right] 當 left == right 時，搜索區間還有一個元素！所以是 left > right 時退出while循環，比如 left == right + 1 ，搜索區間 [right + 1, right] 此時才沒有元素！
• 因此，while 的循環條件就是，left <= right ！
• 如果不小心把上面的寫成 while (left < right) 那么顯然就少了 [right , right] 這個搜索情況沒檢查

細節二：為什么是 left = mid + 1 ，right = mid - 1？
有的代碼是 不加一減一的為啥這里是都加一減一？
這個很簡單理解：
當我們知道mid處的值nums[mid] 根本不是我們要找的target！我們就沒有必要留著mid這個位置了！
自然要去[mid+1, right] 或者[left, mid-1]尋找target了！
mid位置已經尋找過，沒有，自然就是要去掉mid位置。

細節三：這樣寫的缺陷？
如果target在nums中不止只有一個！要尋找其左右邊界，這個算法是做不到的！
比如說給你有序數組 nums = [1,2,2,2,3]，target 為 2，此算法返回的索引是 2，沒錯。但是如果我想得到 target 的左側邊界，即索引 1，或者我想得到 target 的右側邊界，即索引 3，這樣的話此算法是無法處理的。

尋找左側邊界的二分搜索

函數簽名：返回target的左側邊界索引，如果沒有的話返回的是什么？

int left_bound(vector<int>& nums, int target) {
}

這次我用左閉右開 [left, right)

int left_bound(vector<int>& nums, int target) {int right = nums.size();  // 左閉右開 [ l, r )int left = 0;while (left < right) {   	// int mid = left + (right - left) / 2;if (nums[mid] == target) { // 即便是找到了target ，right = mid;         // 收縮上邊界，繼續往左找左邊界		} else if (nums[mid] > target) {right = mid;			// 右開，[left, right)更新為[left, mid)} else if (nums[mid] < target) {left = mid + 1;			// 左閉，[left, right)更新為[mid+1, right)}}	// left == right 時退出循環！ x x t t t x x // 如果找到了target左邊界，return left;
}

細節一：這里while 的循環條件沒有等號了？
因為這次是左閉右開，初始化時：right = n，[left, right) 當left == right 時，搜索區間為空，退出搜索！

細節二：為什么是 left = mid + 1 和 right = mid？
還是因為左閉右開的搜索區間，[left, right) ，當 檢查過 nums[mid] ，并且確定mid 不是我們要找的，下一步應該是去mid 左側或者右側的 左閉右開的區間搜索 [ left , mid) 不包含

• [ left ， mid) 不包含 mid
• [mid + 1，right) 才不含mid

細節三：為什么該算法能夠搜索左側邊界？
上一題的解法就已經可以找到target，但是它的問題在于，只要找到一個target馬上就返回，如果要找target的左邊界，那就需要縮小搜索區間的上界right！

• 即便是找到了 ，即 nums[mid] == target
• 這時候，不返回結果，而是選擇繼續縮小上邊界
• 也就是 right = mid ， 假設mid 左邊還有 target！繼續搜索[left, mid)
• 不斷向左收縮，達到鎖定左側邊界的目的。

細節四：target 不存在時返回什么？
如果 nums 中不存在 target 這個值，計算出來的這個索引含義是什么？如果我想讓它返回 -1，怎么做？
**直接說結論：如果 target 不存在，搜索左側邊界的二分搜索返回的索引是大于 target 的最小索引。**舉個例子，nums = [2,3,5,7], target = 4，left_bound 函數返回值是 2，因為元素 5 是大于 4 的最小元素。

變通一：在一個有序數組中，找到「小于 target 的最大元素的索引」？
// 比如說輸入 nums = [1,2,2,2,3]，target = 2，函數返回 0，因為 1 是小于 2 的最大元素。
// 再比如輸入 nums = [1,2,3,5,6]，target = 4，函數返回 2，因為 3 是小于 4 的最大元素。
答案就是left_bound(nums, target) - 1

int floor(vector<int>& nums, int target) {return left_bound(nums, target) - 1;
}

變通二：如果想讓 target 不存在時返回 -1？
現在left_bound(nums, target)的代碼是：

• 若target存在，返回左側邊界索引
• 若target不存在，返回第一個大于target的元素的索引
  關鍵：
• 分析，target 不存在也是我們搜索出來的結果，也就是不斷收縮左右邊界，最后逼近它可能存在的 區間，有三個可能：
• target 如果存在，在 nums 之中，即不在最前也不在最后邊，這種情況，我們對比 找到的nums[left] 是否 就是我們要找的 target就行！
• 如果 target 比 nums都大？這時，left_bound 會返回 nums.size()，
• 如果 target 比 nums 都小? 這時，left_bound 會返回 -1，
  總結：不存在還分兩種情況，索引越界即<0 或者 >= nums.size() 時直接返回 - 1；
  第二種情況是：找到了一個 left 在索引范圍內，需要判斷 找到的這個值 就是target 的左邊界還是 比 target大的一個元素，target不存在

// 如果不存在 target 不返回 比其大的第一個 元素
int left_bound(vector<int>& nums, int target) {int right = nums.size();  // 左閉右開 [ l, r )int left = 0;while (left < right) {   	// int mid = left + (right - left) / 2;if (nums[mid] == target) { // 即便是找到了target ，right = mid;         // 收縮上邊界，繼續往左找左邊界		} else if (nums[mid] > target) {right = mid;			// 右開，[left, right)更新為[left, mid)} else if (nums[mid] < target) {left = mid + 1;			}}	// 索引越界檢查if (left < 0 || left >= nums.size()) {return -1;}// 檢查nums[left] 是不是 targetreturn nums[left] == target ? left : -1;
}

提示：其實上面的 if 中 left < 0 這個判斷可以省略，因為對于這個算法，left 不可能小于 0
// 你看這個算法執行的邏輯，left 初始化就是 0，且只可能一直往右走，那么只可能在右側越界
// 不過我這里就同時判斷了，因為在訪問數組索引之前保證索引在左右兩端都不越界是一個好習慣，沒有壞處
// 另一個好處是讓二分的模板更統一，降低你的記憶成本，因為等會兒尋找右邊界的時候也有類似的出界判斷

二分搜索最關鍵的一點就是 明確搜索區間！

當然也可以改為左右都閉的寫法！
關鍵還是在于，即便是找到了target，也繼續收縮右邊界！

int left_bound(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;// 搜索區間為 [left, right]while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {// 搜索區間變為 [mid+1, right]left = mid + 1;} else if (nums[mid] > target) {// 搜索區間變為 [left, mid-1]right = mid - 1;} else if (nums[mid] == target) { 	// 即便是找到了也繼續收縮！！// 收縮右側邊界right = mid - 1;}}// 判斷 target 是否存在于 nums 中// 如果越界，target 肯定不存在，返回 -1if (left < 0 || left >= nums.size()) {return -1;}// 判斷一下 nums[left] 是不是 targetreturn nums[left] == target ? left : -1;
}

尋找右側邊界的二分查找

左閉右開寫法：

• 關鍵點：即便是搜索到了target也不返回，而是收縮左邊界！即 left = mid + 1!!
  即：

// 增大 left，鎖定右側邊界
if (nums[mid] == target) {left = mid + 1;// 這樣想: mid = left - 1
}

左閉右開的循環條件是 left <= right!
因為[left, right)， left == right 區間內還有一個元素，需要繼續搜索
只有 left == right + 1時才退出循環！即便是已經確定mid就是要找的target！
left = mid + 1;
可以寫成mid = left - 1
那么答案就要返回left - 1!

所以關鍵點：

• while 循環條件 有等號
• 收縮左邊界，left = mid + 1
• 因為第二點，當mid就是target時有：mid = left - 1，返回target的索引就是left - 1!!

注意這些地方就可以寫出搜索右側邊界的代碼right_bound！

int right_bound(vector<int>& nums, int target) {int left = 0, right = nums.size();while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] == target) {// 注意left = mid + 1;} else if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid;}}// 注意return left - 1;
}

當target 不存在時返回的是什么呢？
當 target 不存在時，right_bound 返回值的含義

直接說結論，和前面講的 left_bound 相反：如果 target 不存在，搜索右側邊界的二分搜索返回的索引是小于 target 的最大索引。

如果不存在target想改成返回-1也和前面類似“

// 計算出left - 1后
// 判斷 target 是否存在于 nums 中
// left - 1 索引越界的話 target 肯定不存在
if (left - 1 < 0 || left - 1 >= nums.size()) {return -1;
}
// 判斷一下 nums[left - 1] 是不是 target
return nums[left - 1] == target ? (left - 1) : -1;

也可以改為兩端都閉的寫法！

int right_bound(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {// 這里改成收縮左側邊界即可left = mid + 1;}}// 最后改成返回 left - 1if (left - 1 < 0 || left - 1 >= nums.size()) {return -1;}return nums[left - 1] == target ? (left - 1) : -1;
}

閉區間寫法中 ，是當 left = right + 1時退出循環 即 right = left - 1時候退出！
而還是因為找到target時，要求繼續收縮左邊界：left = mid + 1
因此右側邊界位置是 mid = left - 1 = right

其實將搜索區間統一成兩端都閉更好記憶！

總結一下：將邏輯進行統一

邏輯統一
梳理一下這些細節差異的因果邏輯：

第一個，最基本的二分查找算法：

因為我們初始化 right = nums.length - 1
所以決定了我們的「搜索區間」是 [left, right]
所以決定了 while (left <= right)
同時也決定了 left = mid+1 和 right = mid-1因為我們只需找到一個 target 的索引即可
所以當 nums[mid] == target 時可以立即返回

第二個，尋找左側邊界的二分查找：

因為我們初始化 right = nums.length
所以決定了我們的「搜索區間」是 [left, right)
所以決定了 while (left < right)
同時也決定了 left = mid + 1 和 right = mid因為我們需找到 target 的最左側索引
所以當 nums[mid] == target 時不要立即返回
而要收緊右側邊界以鎖定左側邊界

第三個，尋找右側邊界的二分查找：

因為我們初始化 right = nums.length
所以決定了我們的「搜索區間」是 [left, right)
所以決定了 while (left < right)
同時也決定了 left = mid + 1 和 right = mid因為我們需找到 target 的最右側索引
所以當 nums[mid] == target 時不要立即返回
而要收緊左側邊界以鎖定右側邊界又因為收緊左側邊界時必須 left = mid + 1
所以最后無論返回 left 還是 right，必須減一

對于尋找左右邊界的二分搜索，比較常見的手法是使用左閉右開的「搜索區間」，我們還根據邏輯將「搜索區間」全都統一成了兩端都閉，便于記憶，只要修改兩處即可變化出三種寫法：

int binary_search(vector<int>& nums, int target) {int left = 0, right = nums.size()-1; while(left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1; } else if(nums[mid] == target) {// 直接返回return mid;}}// 直接返回return -1;
}int left_bound(vector<int>& nums, int target) {int left = 0, right = nums.size()-1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {// 別返回，鎖定左側邊界right = mid - 1;}}// 判斷 target 是否存在于 nums 中if (left < 0 || left >= nums.size()) {return -1;}// 判斷一下 nums[left] 是不是 targetreturn nums[left] == target ? left : -1;
}int right_bound(vector<int>& nums, int target) {int left = 0, right = nums.size()-1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {// 別返回，鎖定右側邊界left = mid + 1;}}// 由于 while 的結束條件是 right == left - 1，且現在在求右邊界// 所以用 right 替代 left - 1 更好記if (right < 0 || right >= nums.size()) {return -1;}return nums[right] == target ? right : -1;
}

總結：

1、分析二分查找代碼時，不要出現 else，全部展開成 else if 方便理解。把邏輯寫對之后再合并分支，提升運行效率。

2、注意「搜索區間」和 while 的終止條件，如果存在漏掉的元素，記得在最后檢查。

3、如需定義左閉右開的「搜索區間」搜索左右邊界，只要在 nums[mid] == target 時做修改即可，搜索右側時需要減一。

4、如果將「搜索區間」全都統一成兩端都閉，好記，只要稍改 nums[mid] == target 條件處的代碼和返回的邏輯即可，推薦拿小本本記下，作為二分搜索模板。

最后我想說，以上二分搜索的框架屬于「術」的范疇，如果上升到「道」的層面，二分思維的精髓就是：通過已知信息盡可能多地收縮（折半）搜索空間，從而增加窮舉效率，快速找到目標。

lc.34 排序數組中查找元素的第一個和最后一個位置！

給你一個按照非遞減順序排列的整數數組 nums，和一個目標值 target。請你找出給定目標值在數組中的開始位置和結束位置。

如果數組中不存在目標值 target，返回 [-1, -1]。

你必須設計并實現時間復雜度為 O(log n) 的算法解決此問題。

示例 1：

輸入：nums = [5,7,7,8,8,10], target = 8
輸出：[3,4]

二維搜索應用泛化

也就是什么問題可以用到二分搜索算法？

什么問題可以運用二分搜索算法技巧？

首先，你要從題目中抽象出一個自變量 x，一個關于 x 的函數 f(x)，以及一個目標值 target。

同時，x, f(x), target 還要滿足以下條件：

1、f(x) 必須是在 x 上的單調函數（單調增單調減都可以）。

2、題目是讓你計算滿足約束條件 f(x) == target 時的 x 的值。

上述規則聽起來有點抽象，來舉個具體的例子：

給你一個升序排列的有序數組 nums 以及一個目標元素 target，請你計算 target 在數組中的索引位置，如果有多個目標元素，返回最小的索引。

這就是「搜索左側邊界」這個基本題型，解法代碼之前都寫了，但這里面 x, f(x), target 分別是什么呢？

我們可以把數組中元素的索引認為是自變量 x，函數關系 f(x) 就可以這樣設定：

// 函數 f(x) 是關于自變量 x 的單調遞增函數
// 入參 nums 是不會改變的，所以可以忽略，不算自變量
int f(int x, vector& nums) {
return nums[x];
}

其實這個函數 f 就是在訪問數組 nums，因為題目給我們的數組 nums 是升序排列的，所以函數 f(x) 就是在 x 上單調遞增的函數。

最后，題目讓我們求什么來著？是不是讓我們計算元素 target 的最左側索引？

是不是就相當于在問我們「滿足 f(x) == target 的 x 的最小值是多少」？

畫個圖，如下：

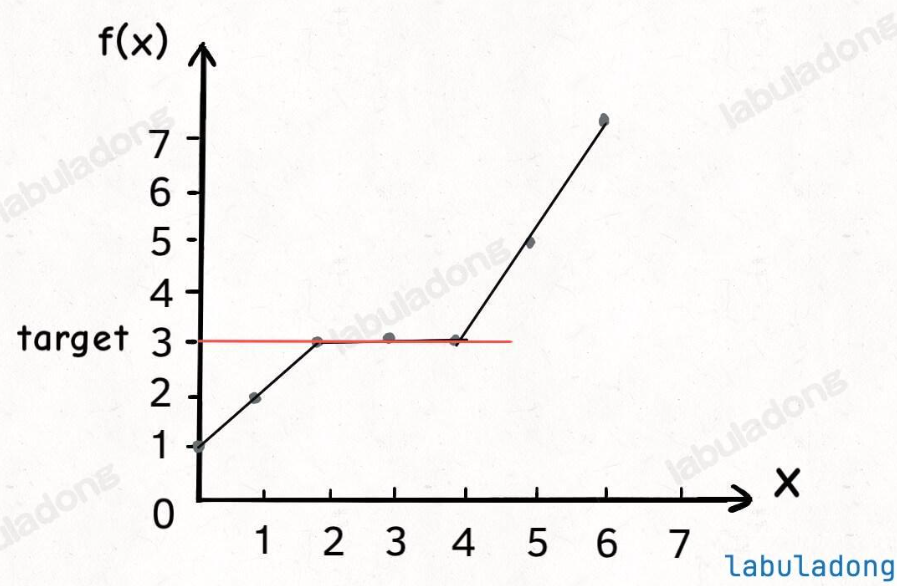
如果遇到一個算法問題，能夠把它抽象成這幅圖，就可以對它運用二分搜索算法。

二分搜索代碼框架

想要運用二分搜索解決具體的算法問題，可以從以下代碼框架著手思考：

// 函數 f 是關于自變量 x 的單調函數
int f(int x) {// ...
}// 主函數，在 f(x) == target 的約束下求 x 的最值
int solution(vector<int>& nums, int target) {if (nums.size() == 0) return -1;// 問自己：自變量 x 的最小值是多少？int left = ...;// 問自己：自變量 x 的最大值是多少？int right = ... + 1;while (left < right) {int mid = left + (right - left) / 2;if (f(mid) == target) {// 問自己：題目是求左邊界還是右邊界？// ...} else if (f(mid) < target) {// 問自己：怎么讓 f(x) 大一點？// ...} else if (f(mid) > target) {// 問自己：怎么讓 f(x) 小一點？// ...}}return left;
}

具體來說，想要用二分搜索算法解決問題，分為以下幾步：

1、確定 x, f(x), target 分別是什么，并寫出函數 f 的代碼。

2、找到 x 的取值范圍作為二分搜索的搜索區間，初始化 left 和 right 變量。

3、根據題目的要求，確定應該使用搜索左側還是搜索右側的二分搜索算法，寫出解法代碼。

下面用幾道例題來講解這個流程。

lc875. 愛吃香蕉的珂珂

珂珂喜歡吃香蕉。這里有 n 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警衛已經離開了，將在 h 小時后回來。

珂珂可以決定她吃香蕉的速度 k （單位：根/小時）。每個小時，她將會選擇一堆香蕉，從中吃掉 k 根。如果這堆香蕉少于 k 根，她將吃掉這堆的所有香蕉，然后這一小時內不會再吃更多的香蕉。

珂珂喜歡慢慢吃，但仍然想在警衛回來前吃掉所有的香蕉。

返回她可以在 h 小時內吃掉所有香蕉的最小速度 k（k 為整數）。

示例 1：

輸入：piles = [3,6,7,11], h = 8
輸出：4
珂珂每小時最多只能吃一堆香蕉，如果吃不完的話留到下一小時再吃；如果吃完了這一堆還有胃口，也只會等到下一小時才會吃下一堆。

他想在警衛回來之前吃完所有香蕉，讓我們確定吃香蕉的最小速度 K。函數簽名如下：

int minEatingSpeed(vector<int>& piles, int H);

1、確定 x, f(x), target 分別是什么，并寫出函數 f 的代碼。
自變量 x 是什么呢？回憶之前的函數圖像，二分搜索的本質就是在搜索自變量。

所以，題目讓求什么，就把什么設為自變量，珂珂吃香蕉的速度就是自變量 x。

那么，在 x 上單調的函數關系 f(x) 是什么？

顯然，吃香蕉的速度越快，吃完所有香蕉堆所需的時間就越少，速度和時間就是一個單調函數關系。

所以，f(x) 函數就可以這樣定義：

若吃香蕉的速度為 x 根/小時，則需要 f(x) 小時吃完所有香蕉。

代碼實現如下：

// 定義：速度為 x 時，需要 f(x) 小時吃完所有香蕉
// f(x) 隨著 x 的增加單調遞減
int f(vector<int>& piles, int x) {int hours = 0;int n = piles.size();// for (int i = 0; i < n; i++) {}return hours;
}

前綴和

差分

隊列/棧

實現隊列/棧

經典

單調棧

單調隊列

二叉樹&遞歸

二叉樹核心框架

遞歸 + 遍歷

遞歸 + 分解

層序遍歷

數據結構設計

LRU

LFU

經典設計

圖論

圖結構通用代碼

圖的邏輯結構

圖的邏輯結構構成：

• 節點vertex
• 邊edge

圖節點的邏輯結構：

// 圖節點實現
class Vertex {
public:int id;std::vector<Vertex*> neighbors;
};

圖其實就是多叉樹：

// 多叉樹節點結構
class TreeNode {
public:int val;std::vector<TreeNode*> children;
};

以上只是邏輯上的構成，實際應用中，很少用這個 Vertex類。

鄰接表和鄰接矩陣實現圖結構

比如一幅圖：

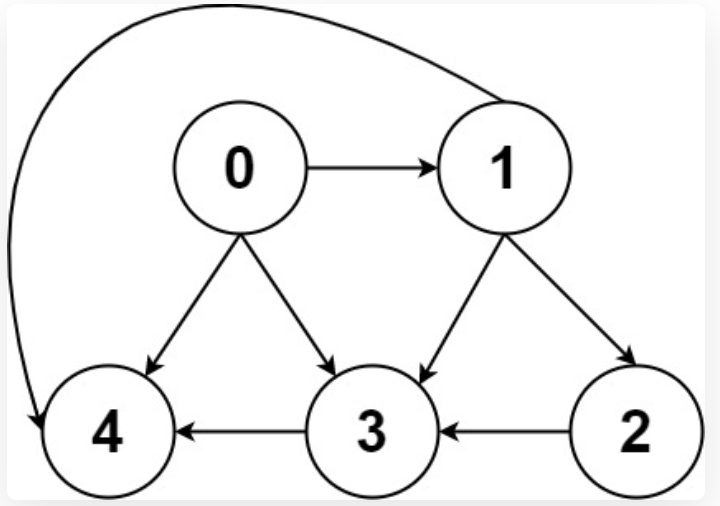
有兩種表示方法：

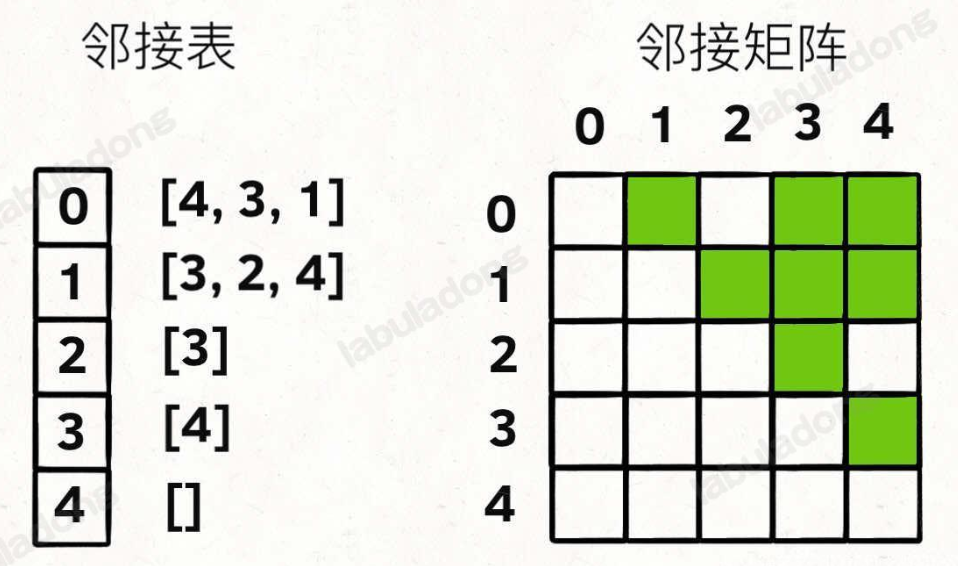
鄰接表很直觀，我把每個節點 x 的鄰居都存到一個列表里，然后把 x 和這個列表映射起來，這樣就可以通過一個節點 x 找到它的所有相鄰節點。

鄰接矩陣則是一個二維布爾數組，我們權且稱為 matrix，如果節點 x 和 y 是相連的，那么就把 matrix[x][y] 設為 true（上圖中綠色的方格代表 true）。如果想找節點 x 的鄰居，去掃一圈 matrix[x][…] 就行了

// 鄰接表：graph[x] 存儲 x 指向的 所有鄰居節點
vector<vector<int>> graph;// 鄰接矩陣：matrix[x][y] 記錄 x 是否有 一條指向 y 的邊
vector<vector<bool>> matrix;

分別適用于不同場景
分析兩種存儲方式的空間復雜度，對于一幅有 V 個節點，E 條邊的圖，鄰接表的空間復雜度是
O
(
V
+
E
)
O(V+E)，而鄰接矩陣的空間復雜度是
O
(
V
2
)
O(V
2
)。

所以如果一幅圖的 E 遠小于 V^2（稀疏圖），那么鄰接表會比鄰接矩陣節省空間，反之，如果 E 接近 V^2（稠密圖），二者就差不多了。

在后面的圖算法和習題中，大多都是稀疏圖，所以你會看到鄰接表的使用更多一些。

鄰接矩陣的最大優勢在于，矩陣是一個強有力的數學工具，圖的一些隱晦性質可以借助精妙的矩陣運算展現出來。不過本文不準備引入數學內容，所以有興趣的讀者可以自行搜索學習。

這也是為什么一定要把圖節點類型轉換成整數 id 的原因，不然的話你怎么用矩陣運算呢？

環檢測

拓撲排序

二分圖判定

并查集

最小生成樹

Dijkstra 最短路徑算法

DFS / 回溯

BFS

動態規劃

動歸核心框架

子序列問題

背包問題

0-1背包問題

物品有兩個屬性：重量wt 和 價值 val
背包有兩個屬性：載重W 和 容量N（最多裝幾個物品）
問：最多能裝多少價值的東西？

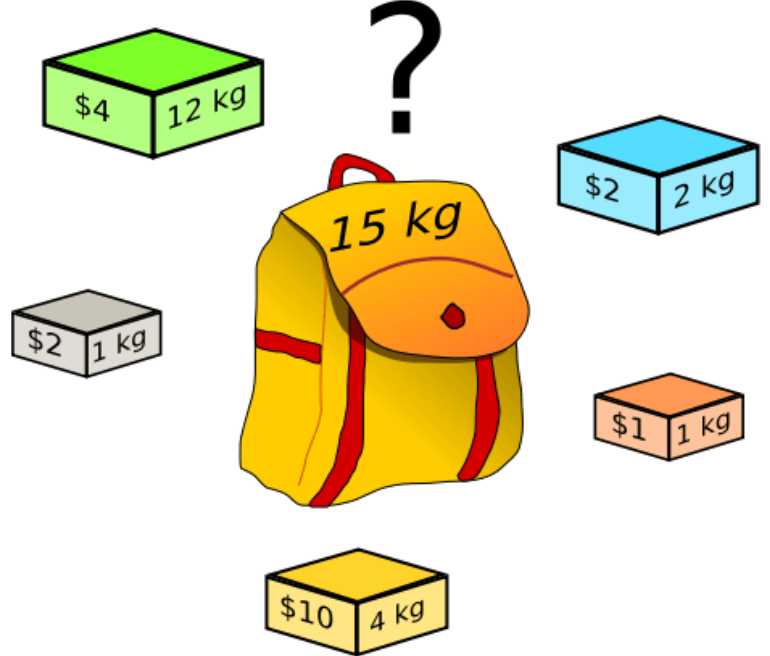
解法：動態規劃
第一步：確定「狀態」和「選擇」
從背包的狀態和物品的狀態出發：

• 狀態：即描述當前問題的局面（即背包的狀態和物品的狀態，不涉及選擇），從「可選擇的前i個物品 」「可用的容量 」；

• 選擇：對于每件商品，選擇「裝進背包」或者「不裝進背包」；

  自頂而下的代碼框架：

  for 狀態1 in 狀態1的所有取值：for 狀態2 in 狀態2的所有取值：for ...dp[狀態1][狀態2][...] = 擇優(選擇1，選擇2...)
  

第二步：定義dp數組， 某個狀態的最優解

• 從狀態出發：涉及兩個東西的狀態，所以需要二維數組dp[ ][ ]；

• dp[ i ][ w ] 定義為：前 i 個物品情況下（ 選擇了某些物品，背包容量剩余 w ）此時，選擇i 以及 w的情況，價值最大為dp[i][w]；

• 例如： dp[3][5] = 6，表示：對于給定的一堆物品，一個背包，若限制從前三個物品選，當選了某些東西，容量為5時最優，價值為6；

• base case：dp[0][…] = dp[][0] = 0，物品數為0或者背包空間為0時，就是base case，為0；

  // 注意，最多N個物品，最大W的容量
  int[][] dp[N][W];
  dp[0][...] = 0;
  dp[...][0] = 0;
  for i in [1...N]:for w in [1...W]:dp[i][w] = max {把物品 i 放進背包不放 i}
  return dp[N][W];
  

第三步：根據「選擇」，思考狀態轉移的邏輯

從dp定義出發：dp[i][w] 表示：對于前 i 個物品（從 1 開始計數），當前背包的容量為 w 時，這種情況下可以裝下的最大價值是 dp[i][w]。
關鍵的選擇是：

• 如果沒有把第i個物品放入背包（w沒有變）：dp[i][w]直接繼承dp[i-1][w]，dp[i][w] = dp[i-1][w]
• 如果把第i個物品放入背包：dp[i][w] = val[i] + dp[i-1][W-wt[i-1]];(要在剩余容量的限制下，在前i-1個里面挑選，求最大值，也就是dp[i-1][W-wt[i-1]])

for i in [1..N]:for w in [1..W]:dp[i][w] = max(dp[i-1][w],dp[i-1][w - wt[i-1]] + val[i-1])
return dp[N][W]

最后一步：邊界條件處理

#include <cassert>
// W 背包限重，wt[]，val[]
int knapsack(int W, vector<int>& wt, vector<int>& val) {int N = val.size();// 定義dp 并直接初始化0// dp[i][w] 限制前i個可選 + 限重w 時的最大價值vector<int> dp(N + 1, vector<int>(W + 1));for (int i = 1; i <= N; i++) { 			// 狀態1：for (int w = 1; w <= W; w++) {		// 狀態2：// 注意處理，可能有的物品wt[i]重量大于當前限重w// 則直接跳過dp[i][w]?那只能說明不能選i// 強制不選i，即dp[i][w] = dp[i-1][w]if (wt[i] > w) {dp[i][w] = dp[i-1][w];}else { dp[i][w] = max(val[i] + dp[i-1][w-wt[i]] // 選擇1dp[i-1][w]				 // 選擇2);}}}return dp[N][W];
}

474. 一和零

vector<int> dp(N+1, vector<int>(W + 1));
dp[i][w]	// 只能【選前i個物品】，【限重w】情況下，最大價值為dp[i][w]

dp[i][j][k]	// 只能【選前i個物品】，【0 最大限制j個】【1 最大限制k個】情況下，最大數量為dp[i][j][k]

class Solution {
public:int findMax(vector<string>& strs, int m, int n) {// 定義dp：dp[][][]// 如果只能選前i個元素，最多選j個0，最多選k個1；// 可以裝的最大字符串數為 dp[i][j][k]// 注意三維數組的定義方式l = strs.size();vector<vector<vector<int>>> dp(l + 1, vector<vector<int>>(m + 1, vector<int>(n + 1, 0)));// base case：dp[0][...][...] = 0 沒有任何字符串可選時，最大可裝的數量是0// 從 base case 開始狀態轉移 ， 從 1 到 nfor (int i = 1; i <= l; i++) {// 注意存在一個索引偏移，dp[i][][] 的i是第i個的意思，對應到strs 的當前char索引是i-1string curStr = strs[i - 1];// 統計當前curStr(物品)的0數量和1數量(重量)int zeroCount = 0;int oneCount = 0;for (char c : curStr) {if (c == '0') zeroCount++;else oneCount++;}// 根據要不要選 curStr 進行狀態轉移for (int j = 0; j <= m;j++) {for (int k = 0; k <= n;k++) {// 檢查當前物品curStr的重量zeroCount oneCount是否小于背包容量限制為j和kif (j >= zeroCount && k >= oneCount) {dp[i][j][k] = max(dp[i - 1][j][k],1 + dp[i - 1][j - zeroCount][k - oneCount]										);} else {					// 背包容量不足時，強制選擇不放curStr！dp[i][j][k] = dp[i - 1][j][k];	// }}} }// return dp[l][m][n];}
};

1262. 可以被3整除的最大和

// 定義dp
dp = vector<int>(nums.size());

class Solution {
public:int maxSumDivThree(vector<int>& nums) {// 定義：nums[0..i] 中，和 3 相除余數為 j 的最大和是 dp[i][j]// 3 is dp[i][j]int n = nums.size();// dp[0][0/1/2]要作為base case，所以總共有n+1個情況vector<vector<int>> dp(n + 1, vector<int>(3, INT_MIN));// base casedp[0][0] = 0;dp[0][1] = INT_MIN;dp[0][1] = INT_MIN;// 狀態轉移方程：根據第i個數字nums[i]以及前i-1個數字的余數情況dp[i-1][1/2/3]// 來推導前i個數字的余數情況 dp[i][0/1/2] for (int i = 1; i <= nums; i++) {int curNum = nums[i - 1]; if (curNum % 3 == 0) {	// 當前元素curNum余數0，則前面元素和余數是多少，加上curNum之后還是多少，就看要不要加curNum【選擇】dp[i][0] = max(curNum + dp[i - 1][0], dp[i - 1][0]);dp[i][1] = max(curNum + dp[i - 1][1], dp[i - 1][1]);dp[i][2] = max(curNum + dp[i - 1][2], dp[i - 1][2]);} else if (curNum % 3 = 1) { 	// 選不選余數為1的curNum？dp[i][0] = max(curNum + dp[i - 1][2], dp[i - 1][0]);dp[i][1] = max(curNum + dp[i - 1][0], dp[i - 1][1]);dp[i][2] = max(curNum + dp[i - 1][1], dp[i - 1][2]);} else { // curNum余數是2dp[i][0] = max(curNum + dp[i - 1][1], dp[i - 1][0]);dp[i][1] = max(curNum + dp[i - 1][2], dp[i - 1][1]);dp[i][2] = max(curNum + dp[i - 1][0], dp[i - 1][2]);		}}// 最后返回前i個元素的能被3整除最大和，即余數為0，dp[n][0]return dp[n][0];}
};

1235. 規劃兼職工作

這次物品變成了不同的工作，每份工作有開始時間、結束時間、以及對應的價值，收益。
當然不可能分身，所以同一個時刻只能做一份工作，返回最大收益。
這也是0-1的變種問題：
0-1的狀態是【前i個物品】【限重w】情況下，【選擇】選不選當前的物品，使得當前價值最大；
這里的物品就是工作，工作有【開始時間】【結束時間】【收益】三個屬性，打包到一起，【選擇】選不選當前的工作，使得收益最大。
狀態是：【前i個工作可選】？直接用endTime作為可選時間吧！

class Solution {
public:int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {// 物品的三個屬性打包到一起，方便排序int n = profit.size();vector<vector<int>> jobs(n, vector<int>(3));for (int i = 0; i < n;i++) {jobs[i] = {startTime[i], endTime[i], profit[i]};}// 用sort(起始，結束（開區間）， 排序規則 )；按end時間排序sort(jobs.begin(), jobs.end(), [](const vector<int> a, vector<int> b) {return a[1] < b[1];});// 至此已經按照一定順序排列好了 “物品”map<int, int> dp;for (const auto& job : jobs) {// 提取出job的三個屬性  int begin = job[0];int end = job[1];int value = job[2];// 進行選擇，窮舉所有選擇dp[end] = max(// 選當前job，收益增加value，但是[begin, end)這段時間被占用了！// [begin, end)時間段內的工作都不行，[0,begin)內的任務可以// 用二分手段查找第一個結束時間大于等于begin的dp結果：dp.upper_bound(begin)// 這個的前一個prev就是不在[begin, end)區間內的選擇的最大收益// 最后一個鍵 <= begin 的元素迭代器// dp<int, int> 第一個元素鍵是截至end ： 第二個元素值是收益value + prev(dp.upper_bound(begin))->second,// 不選當前job，則當前job[end]的值直接繼承上一個end的值(保存現有最大值)dp.rbegin()->second; // rbegin()指向容器最后一個元素);}return dp.rbegin()->second;}
};

子集背包問題——LC.416 分割等和子集

輸入一個只包含正整數的非空數組 nums，請你寫一個算法，判斷這個數組是否可以被分割成兩個子集，使得兩個子集的元素和相等。
比如說輸入 nums = [1,5,11,5]，算法返回 true，因為 nums 可以分割成 [1,5,5] 和 [11] 這兩個子集。
如果說輸入 nums = [1,3,2,5]，算法返回 false，因為 nums 無論如何都不能分割成兩個和相等的子集。

這個問題看起來和背包沒啥關系啊？
0-1背包問題：求出【可裝載重量W】【N個物品（每個物品價值v，重量w）】情況下，求出背包可裝載最大價值。
分割子集要求：判斷能否分割成兩個和相等的子集，實際上，如果有一個子集可以湊成sum/2，另一半必然就是sum/2呀！
所以問題轉化成了，背包【可裝載重量 = sum/2】【N個物品（每個物品有重量nums[I]）】，問能不能恰好裝滿背包。

解法：
第一步：明確【狀態】和【選擇】

• 狀態：跟0-1背包一樣的，【可選擇的物品】【背包當前容量】
• 選擇：當前物品【裝】【不裝】

第二步：dp數組定義？base case？

• dp[i][j] = x：對于前i個物品可選（i從1開始計數？）， 背包容量j時，x為true表示可以裝滿，false表示不能恰好裝滿
• base case：沒有物品可選時，dp[0][…] = 0；容量為0時，天然裝滿dp[…][0] = true；
• 最終返回的：N個物品時，能不能剛好湊到sum/2，return dp[N][sum/2]
• 舉例：dp[4][9] 若只在前4個物品選擇，有一種方案能夠恰好把容量9的背包裝滿；或對于這道題，若只在前4個數字選擇，存在一個子集的和為9；

第三步：根據【選擇】分析狀態轉移的邏輯
也就是裝不裝第i個物品的問題（）：

• 不裝：直接繼承dp[i-1][j]
• 裝：取決于dp[i-1][j - nums[i]]，如果裝了第 i 個物品，就要看背包的剩余重量 j - nums[i-1] 限制下是否能夠被恰好裝滿。如果 j - nums[i-1] 的重量可以被恰好裝滿，那么只要把第 i 個物品裝進去，也可恰好裝滿 j 的重量；否則的話，重量 j 肯定是裝不滿的。

注意點：

• 上述分析都是第i個物品，所以與真實的nums索引差1
• 和為奇數的時候，必不可分
• 第i個物品（索引為i-1）的重量（nums[i - 1]） 大于背包總容量j時候，強制選擇不裝，裝不了！

class Solution {
public:	bool canPartition(vector<int>& nums) {// 求sumint sum = 0;for (int num : nums) sum += num;// sum 為奇數，直接falseif (sum % 2 != 0) return false;// sum 偶數，繼續int W = sum / 2;	// 定義dp[i][j]： i范圍是0~n，j范圍是0~Wint n = nums.size();vector<vector<int>> dp(n + 1, vector<int>(w + 1, false));// base case：初始化dp[0...n][0] = turefor (int i = 0; i >= n; i++) {dp[i][0] = true;			}// 狀態轉移：前提背包容量夠， 且注意索引for (int i = 1; i <= n;i++) {	// 第i個選不選，索引是nums[i-1]選不選for (int j = 1; j <= W; j++) {	//// 如果 容量j 是足夠的if (j >= nums[i - 1]) {// 裝還是不裝？dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];} else {	// 容量不夠,肯定是裝不了第i個物品 nums[i - 1]dp[i][j] = dp[i - 1][j];}}}// 返回return dp[n][W];}
};

優化空間復雜度，因為這道題的dp[i][j] 全靠上一行 dp[i - 1][…]轉化過來！
之前的元素都不會在用，不用保存所有的行！

class Solution {
public:	bool canPartition(vector<int>& nums) {// 求sumint sum = 0;for (int num : nums) sum += num;// sum 為奇數，直接falseif (sum % 2 != 0) return false;// sum 偶數，繼續int W = sum / 2;	// 定義dp[i][j]： i范圍是0~n，j范圍是0~Wint n = nums.size();// vector<vector<int>> dp(n + 1, vector<int>(w + 1, false));vector<int> dp(W + 1, false);// base case：初始化dp[0...n][0] = ture 即dp[0] = true// for (int i = 0; i >= n; i++) dp[i][0] = true;dp[0] = true;// 狀態轉移：前提背包容量夠， 且注意索引for (int i = 0; i < n; i++) {	// 第i個選不選，索引是nums[i-1]選不選for (int j = 1; j <= W; j++) {	//// 如果 容量j 是足夠的if (j >= nums[i]) {// 裝還是不裝？dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];}}}}// 返回// return dp[n][W];return dp[W];}
};

這段代碼和之前的解法思路完全相同，只在一行 dp 數組上操作，i 每進行一輪迭代，dp[j] 其實就相當于 dp[i-1][j]，所以只需要一維數組就夠用了。
唯一需要注意的是 j 應該從后往前反向遍歷，因為每個物品（或者說數字）只能用一次，以免之前的結果影響其他的結果。
至此，子集切割的問題就完全解決了，時間復雜度O(n*sum)，空間復雜度
這句話沒讀懂啊，為啥會影響之前的其他結果？
為啥原來二維數組不用反向遍歷？二維數組不能反過來遍歷吧，前一個值都沒有算出來，反過來不就不能利用上一個計算出來的值了嗎？

chase4ever
Tokics
2023-04-19
這個要慢慢品，我理解了好久才悟到。

為什么不能正向遍歷？因為外層遍歷的是物品，0-1背包問題，一個物品只能選擇一次，就是說，如果j正向遍歷，容量從小到大可能多次選擇這個品。
2.反向遍歷，前面的數據都沒計算，為什么j反向遍歷正確？ 因為在計算dp[i][j]的時候，使用的是dp[i-1][j-v]的數據，即：只考慮0~i-1這么多物品的情況下的結果。這些都是完全計算過了的，反向遍歷沒有問題，且，反向遍歷可以保證在j之前的容量里，一定沒有考慮過這個物品。也就是說，當前可以決策是否裝入i這個物品，是因為在這之前的容量沒有考慮過是否裝入i，保證i只能最多裝入1次

子集背包問題——最后一塊石頭的重量II

有一堆石頭，用整數數組 stones 表示。其中 stones[i] 表示第 i 塊石頭的重量。

每一回合，從中選出任意兩塊石頭，然后將它們一起粉碎。假設石頭的重量分別為 x 和 y，且 x <= y。那么粉碎的可能結果如下：

如果 x == y，那么兩塊石頭都會被完全粉碎；
如果 x != y，那么重量為 x 的石頭將會完全粉碎，而重量為 y 的石頭新重量為 y-x。
最后，最多只會剩下一塊 石頭。返回此石頭 最小的可能重量 。如果沒有石頭剩下，就返回 0。

這道題完全就是分割子集的變形題，每次碰碎出兩塊石頭，得到y-x！要求出最后剩余的石頭的最小值，分割子集問題中要找出是否存在兩個相等子集，
舉上一題的例子：
比如說輸入 nums = [1,5,11,5]，算法返回 true，因為 nums 可以分割成 [1,5,5] 和 [11] 這兩個子集。
如果說輸入 nums = [1,3,2,5]，算法返回 false，因為 nums 無論如何都不能分割成兩個和相等的子集。
這里 nums = [1,5,11,5]，這里 11 碰 1 得到 10 ，10 碰 5 得到 5， 5 碰 5，最后是0；
nums = [1,3,2,5]，這里 5 碰了 1 得到 4，4 碰了 2 得到 2， 2 碰 3 得到 1；

其實就是分割子集，使得子集的差最小，也就是使得兩個子集的重量和都盡量接近sum/2！

所以問題轉換成了背包問題：
給定容量sum/2的背包，若干石頭stones，問背包能裝下的最大重量maxWeight是？則一堆重量和是maxWeight，另外一堆重量和（sum - maxWeight）是最后返回（sum - maxWeight） - maxWeight；這就是消除不掉的石頭的重量和！

所以

• dp[i][j] 定義：僅可以選擇前i個石頭，容量是j情況下，裝的最大重量dp[i][j]
• base case ：
  • dp[0][…] = 0
  • dp[…][0] = 0
• 狀態轉移：選不選第i個（索引變換）石頭？
  • 石頭巨大，超容量j：強制不選，繼承上個值
  • 可選可不選 第i個石頭，stone[i - 1]：
    • 選stone[i - 1]： stone[i - 1] + dp[i ][j - stone[i - 1]]
    • 不選：繼承

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {// 計算 sumint sum = 0;for (int stone : stones) sum += num;// 定義dp[i][j]：前i個石頭可選，背包容量j 情況下，最多多重？  // i范圍0~n 長度n+1， j范圍0~W 長度W+1int n = stones.size(), W = sum / 2; vector<vector<int>> dp(n + 1, vector<int>(W + 1, 0));// base case：已經初始化！for (int i = 1; i <= n; i++) {int curStone = stones[i - 1];	// 索引問題for (int j = 1; j <= W; j++) {if (j < curStone) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = max(dp[i - 1][j],curStone + dp[i - 1][j - curStone]);}}}int maxWeight = dp[n][W];return sum - maxWeight * 2;}
};

完全背包問題——零錢兌換II

給你一個整數數組 coins 表示不同面額的硬幣，另給一個整數 amount 表示總金額。

請你計算并返回可以湊成總金額的硬幣組合數。如果任何硬幣組合都無法湊出總金額，返回 0 。

假設每一種面額的硬幣有無限個。

輸入：amount = 5, coins = [1, 2, 5]
輸出：4
解釋：有四種方式可以湊成總金額：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

很容易看出也是個背包類型的問題，跟前面最大的區別就是物品數量無限，稱為完全背包問題。

第一步：確定狀態和選擇
狀態：

• 背包的容量
• 可選擇的物品
  選擇：
• 裝進背包
• 不裝進背包
  動歸框架：

for 狀態1 in 狀態1的所有取值：for 狀態2 in 狀態2的所有取值：for ...dp[狀態1][狀態2][...] = 計算(選擇1，選擇2...)

第二步：定義dp，要能從子問題推出新問題的dp！
從題意：求解湊出某個金額amout的方案數量，并且有兩個狀態可選擇的物品和湊的金額
定義dp[i][j] : 若只能選前i種（注意！這里換成了“種”）物品（不限制數量，可重復），當容量j時，有dp[i][j]種方法可以填滿背包容量j
換成這道題背景：
若只使用 coins 中的前 i 個（i 從 1 開始計數）硬幣的面值，若想湊出金額 j，有 dp[i][j] 種湊法
base case ：

• dp[0][…] = 0；這一步很好想，沒有選擇，則方案必然為0
• dp[…][0] = ？；目標金額是0呢？什么都不做就已經完成目標金額，什么都不做是唯一的一個方案！dp[…][0] = 1；
  最終返回什么：return dp[n][amount]

偽代碼：

int dp[N+1][amount+1]
dp[0][..] = 0
dp[..][0] = 1for i in [1..N]:for j in [1..amount]:把物品 i 裝進背包,不把物品 i 裝進背包
return dp[N][amount]

第三步：根據選擇，思考動態轉移

dp[i][j] 是「共有多少種湊法」
是只有前i“種”選擇
選擇：

• 如果我們不把第i種物品放入背包：不使用coins[i - 1]這種硬幣，那么湊出面額j的方法數為dp[i - 1][j]
• 如果我們把第i種物品放入背包：即使用coins[i - 1]這種硬幣，那么我們要關心的是如何湊出j - coins[i - 1]， 那么 dp[i][j] = dp[i][j - coin[i - 1]] 注意這里不是i - 1！而是用的同樣i時的 容量更小的時候的dp[i][j - coin[i - 1]]
• 然后把選不選兩種選擇的方案數量！加到一起就是 總的方案數量！dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]]

Note

有的讀者在這里可能會有疑問，不是說可以重復使用硬幣嗎？那么如果我確定「使用第 i 個面值的硬幣」，我怎么確定這個面值的硬幣被使用了多少枚？簡單的一個 dp[i][j-coins[i-1]] 可以包含重復使用第 i 個硬幣的情況嗎？

對于這個問題，建議你再仔回頭細閱讀一下我們對 dp 數組的定義，然后把這個定義代入 dp[i][j-coins[i-1]] 看看：

若只使用前 i 個物品（可以重復使用），當背包容量為 j-coins[i-1] 時，有 dp[i][j-coins[i-1]] 種方法可以裝滿背包。

看到了嗎，dp[i][j-coins[i-1]] 也是允許你使用第 i 個硬幣的，所以說已經包含了重復使用硬幣的情況

class Solution {
public:int change(int amount, vector<int>& coins) {// 定義dp[i][j]int n = coins.size();vector<vector<int>> dp(n + 1, vector<int>(amount + 1, 0));// base case：dp[][0]for (int i = 0; i <= n; i++) dp[i][0] = 1;// for (int i = 1; i <= n;i++) {int curCoin = coins[i - 1];for (int j = 1; j <= amount; j++) {if (j < curCoin) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j] + dp[i][j - curCoin];				}		}}return dp[n][amount];}
};

這道題只用到了，最近的兩行狀態dp！
思考如何空間壓縮？如何記憶化搜索實現時間復雜度優化？

背包問題變體——494.目標和

打家劫舍

股票問題

貪心算法

數學

位操作

位操作是直接對整數的二進制位（0 或 1）進行運算的操作，是計算機底層數據處理的基礎方式。它通過特定運算符對二進制位進行邏輯或移位處理，具有運算速度快（CPU 直接支持）、內存占用少等特點，廣泛用于底層編程、算法優化、數據壓縮等場景。

位運算核心優勢：

• 效率極高：位運算直接在 CPU 層面執行，比加減乘除等運算更快。
• 節省空間：可用二進制位表示多個狀態（如用 1 個字節存儲 8 個布爾值）。
• 功能獨特：特定問題，狀態壓縮、加密、奇偶判斷等

常見應用場景

• 算法優化（如計算漢明重量、判斷 2 的冪次方）。
• 數據加密（如異或加密）。
• 嵌入式編程（操作硬件寄存器）。
• 狀態壓縮（用二進制位表示多個開關狀態）。

核心運算符

1. 與（&）：兩個位都為 1 時，結果為 1；否則為 0。
   例：5（101） & 3（011） = 1（001）
2. 或（|）：兩個位中至少有一個為 1 時，結果為 1；否則為 0。
   例：5（101） | 3（011） = 7（111）
3. 非（~）：將位 0 變為 1，1 變為 0（注意符號位處理，不同語言有差異）。
   例：~5（000…0101） = …11111010（取決于整數位數）
4. 異或（^）：兩個位不同時（一個 0 一個 1），結果為 1；相同則為 0。
   例：5（101） ^ 3（011） = 6（110）
5. 左移（<<）：將二進制位向左移動指定位數，右側補 0。
   例：5（101） << 1 = 10（1010）（相當于 ×2）
6. 右移（>>）：將二進制位向右移動指定位數，左側補符號位（正數補 0，負數補 1）。
   例：5（101） >> 1 = 2（10）（相當于 ÷2 取整）

環形數組的位運算優化：index & (arr.length - 1)

1. 環形數組的常規實現：模運算 % 取余

環形數組需模擬 “頭尾相接” 的循環遍歷，常規做法是用模運算（取余運算）%計算索引：

• 當index遞增時，index % arr.length可循環獲取數組元素
• 示例（數組[1,2,3,4]）：
• (sizeof(arr) / sizeof(int) == 數組長度 arr.length

int arr[] = {1, 2, 3, 4};
int index = 0;
while (true) {// (sizeof(arr) / sizeof(int) == 數組長度 4cout << arr[index % (sizeof(arr) / sizeof(int))] << endl;index++;
}
// 輸出：1,2,3,4,1,2,3,4,1,2,3,4...

缺點：模運算%對計算機而言是較昂貴的操作，性能較低。

2. 優化方案：&運算替代%

技巧題

補充高頻題

42.接雨水

給定 n 個非負整數表示每個寬度為 1 的柱子的高度圖，計算按此排列的柱子，下雨之后能接多少雨水。

輸入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
輸出：6
解釋：上面是由數組 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度圖，在這種情況下，可以接 6 個單位的雨水（藍色部分表示雨水）。

接下來由淺入深介紹暴力解法 -> 備忘錄解法 -> 雙指針解法，在 O(N) 時間 O(1) 空間內解決這個問題。

解法一：暴力

簡化問題的方法：

• 從問題局部開始思考
• 寫出簡單粗暴的解法
• 逐步優化

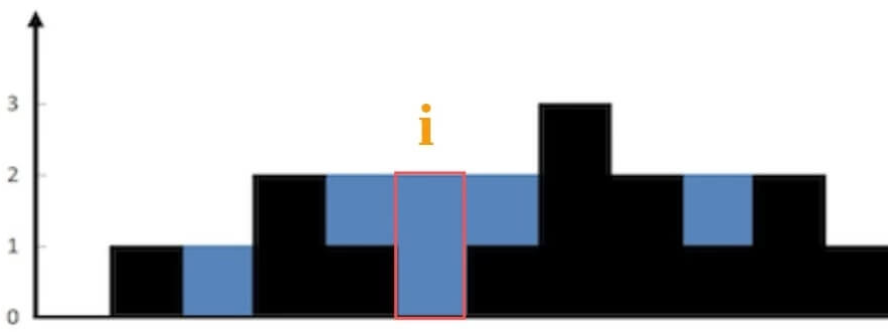
比如先放棄整體思考，而是思考某個位置i能裝多少水：

• 這個位置能裝2格水，因為height[i] = 0，而水平線在高度為2的位置，2 - 0 = 2；
• 為什么水平線高度為2？
  • 取決于 min（往左邊找最高的柱子高，往右邊找最高的柱子）
  • 即min（max(height[0…i]),max( height[i…end])） - height[i]
    
    
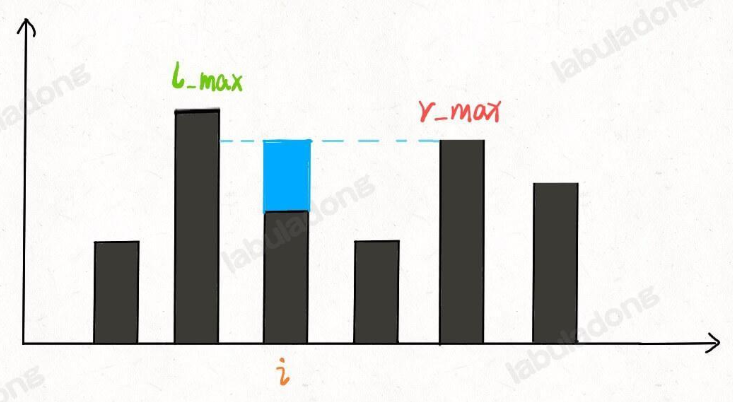
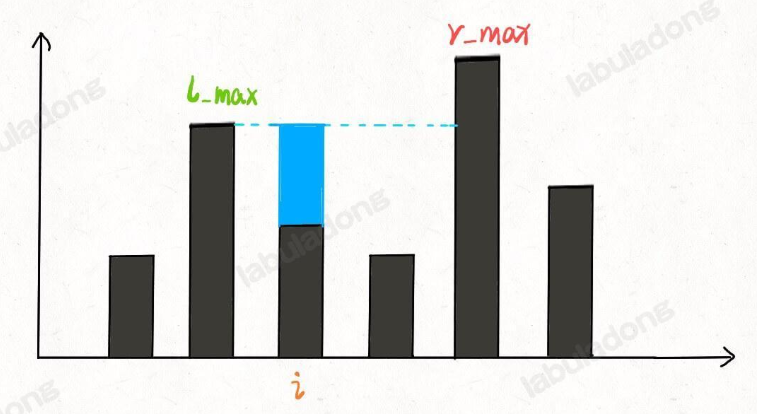
    這就是本題核心思路：

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int res = 0;for (int i = 1; i < n - 1;i++) {int l_max = 0;int r_max = 0;for (int j = i; j >= 0; j--) {// 往左找 l_maxl_max = max(l_max, height[j]);// }for (int j = i;) {r_max = max(r_max, height[j]);}res += min(l_max, r_max) - height[i];}return res;}
};

時間復雜度$O(N^2)$
問題出在，尋找左右兩邊的r_max 和 l_max 的方式非常笨拙。

注意：尋找左右最高點的時候，出發點是自身，包含自身的！如果自身就是最高，則i左右高點都是自身，后續計算res時減去自身就是0!

解法二：備忘錄優化
每個位置 i 都要計算 r_max 和 l_max 嗎？我們直接把每個位置需要的r_max 和 l_max結果都提前計算出來，記錄下來不就行了！
將解法一中的 r_max 和 l_max 改進為 數組 r_max[i] 和 l_max[i]

• l_max[i] 表示位置 i 左邊最高的柱子高度；
• r_max[i] 表示位置 i 右邊最高的柱子高度

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int res = 0;// 雙備忘錄vector<int> l_max(n);	// l_max[i] 表示 i 左邊最大的柱子高vector<int> r_max(n);// 初始化備忘錄l_max[0] = height[0];r_max[n - 1] = height[n - 1];// 從左向右計算l_maxfor (int i = 1; i < n; i++) {	// i 左側最高高度，包含 i 自身l_max[i] = std::max(height[i], l_max[i - 1])}// 從右往左計算r_maxfor (int i = n - 2; i >= 0; i--) {r_max[i] = std::max(height[i], r_max[i + 1])}		// 計算答案for (int i = 1; i <= n - 2; i++) {res += std::min(l_max[i], r_max[i]) - height[i];}return res;}
};

其實思路完全就是解法一的暴力，只是避免了重復計算，算是空間換時間，時間復雜度優化到$O(N)$，但是空間復雜度也是$O(N)$。

有什么辦法能優化空間復雜度？

解法三：雙指針

class Solution {
public:int trap(vector<int>& height) {// 左右指針int n = height.size();int left = 0;int right = n - 1;// 定義int l_max = 0;int r_max = 0;int res = 0;while (left < right) {l_max = max(l_max, height[left]);r_max = max(r_max, height[right]);// res += min(l_max, r_max) - height[i]if (l_max < r_max) {	// 左邊低res += } else {  				// 右邊高 }}}};