一、隨機變量

隨機變量是一個將 隨機事件 映射到 數值 的數學函數，用于描述事件的結果。隨機變量可以是離散的（如骰子）或連續的（如人的身高、體重）。

1）概率質量函數PMF——離散隨機變量

????????P(X = x) = 對應于某個值 ( x 的概率）

2）概率密度函數PDF——連續隨機變量

????????f(x) 描述隨機變量在某點的概率密度。連續變量的概率在區間上求和：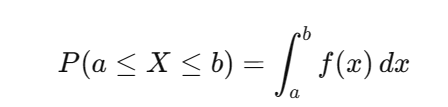

3）累計分布函數CDF：表示隨機變量小于或等于某值的累計概率：

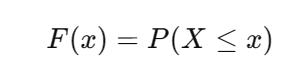
F(x) 對離散變量是 PMF 的累加，對連續變量是 PDF 的積分。

二、隨機變量的期望和方差

明確了公式之后，就需要描述出來。既然概率是一個分布，那么使用期望與方差描述

2.1 期望

反映隨機變量的平均值，用于衡量其中心位置

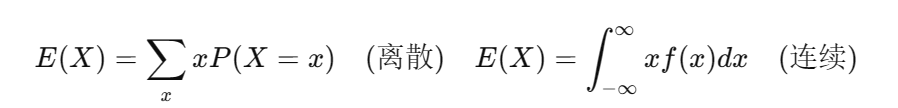
2.2 方差

衡量隨機變量的分布范圍或波動大小

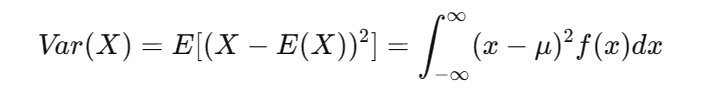
2.3 協方差和相關系數

描述兩個隨機變量之間的關系

2.4 正態分布中期望和方差的圖形

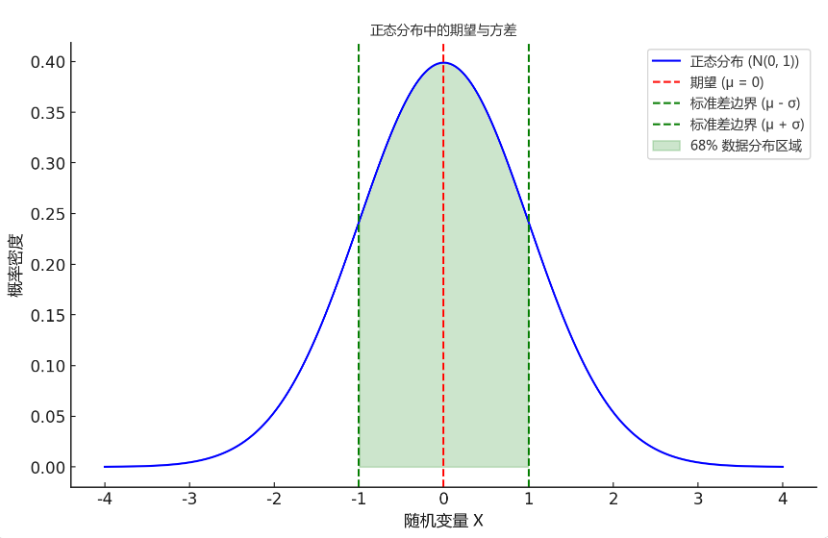
真實場景下：如果想要說明留存率50%是合理的還是不合理的。可以看他的分布，用期望去描述分布，方差去衡量變化。

三、多維隨機變量與聯合分布

如在參加活動的基礎上，描述【歷史有參加活動且有付費行為的用戶】再次參加活動的概率。就涉及到了多維變量和聯合分布相關

3.1?多維隨機變量的定義

1）聯合分布

聯合概率 P(X=x,Y=y)（離散型） 或 聯合概率密度函數 f(x,y)（連續型），描述兩個或多個變量的聯合行為。公式：

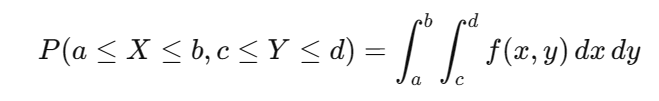
2）邊緣分布

從聯合分布中提取單個變量的分布。例如 fX?(x)

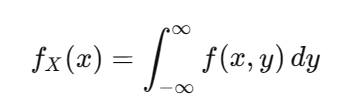
3）條件分布

在已知條件下計算變量的概率分布。例如 P(X∣Y=y) 或 f(X∣Y)

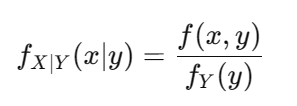
4）條件均值

聯合正態分布下，給定 Y=y0? 時，X 的條件均值 E(X∣Y=y0?) 可以表示為

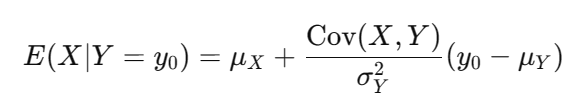
5）協方差和相關系數

協方差描述兩個變量是否相關

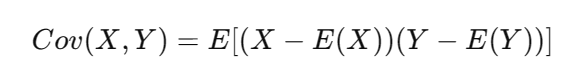
相關系數標準化協方差，取值范圍為 [-1, 1]

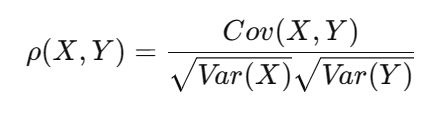
總結：概率分布是對事件過程的描述，因此不僅要拆解指標維度（比如分城市、用戶層級），拆解訂單量。對于留存率類的指標，也需要查看分布。描述概率分布，能清楚知道中間發生了什么。