機器學習（重學版）基礎篇（概念與評估）

?本篇參考周志華老師的西瓜書，但是本人學識有限僅能理解皮毛，如有錯誤誠請讀友評論區指正，萬分感謝。

一、基礎概念與評估方法

本節目標：建立理論基礎框架?

1、機器學習定義

機器學習是一門通過計算手段利用經驗（以數據形式存在）改善系統性能的學科。其核心是研究 “學習算法”—— 通過該算法，輸入經驗數據可生成 “模型”，模型能對新情況（如未見過的樣本）做出判斷。
形式化定義：若計算機程序通過經驗 E，在任務類 T 上的性能（以 P 評估）得到改善，則稱該程序對 E 進行了學習。

我的理解：

機器學習是讓計算機從數據中自動學習規律（模型），從而提升其完成特定任務（如預測、識別）能力的技術。

六維核心要點：

目標：?改善系統在特定任務上的性能
手段：?利用計算處理數據（經驗）
核心：?學習算法
產物：?模型
關鍵能力：?模型能對新情況（未見過的數據）做出有效判斷（泛化能力）
衡量：?性能指標（P）的提升

數據 -> 算法 -> 模型 -> 預測 -> 提升?

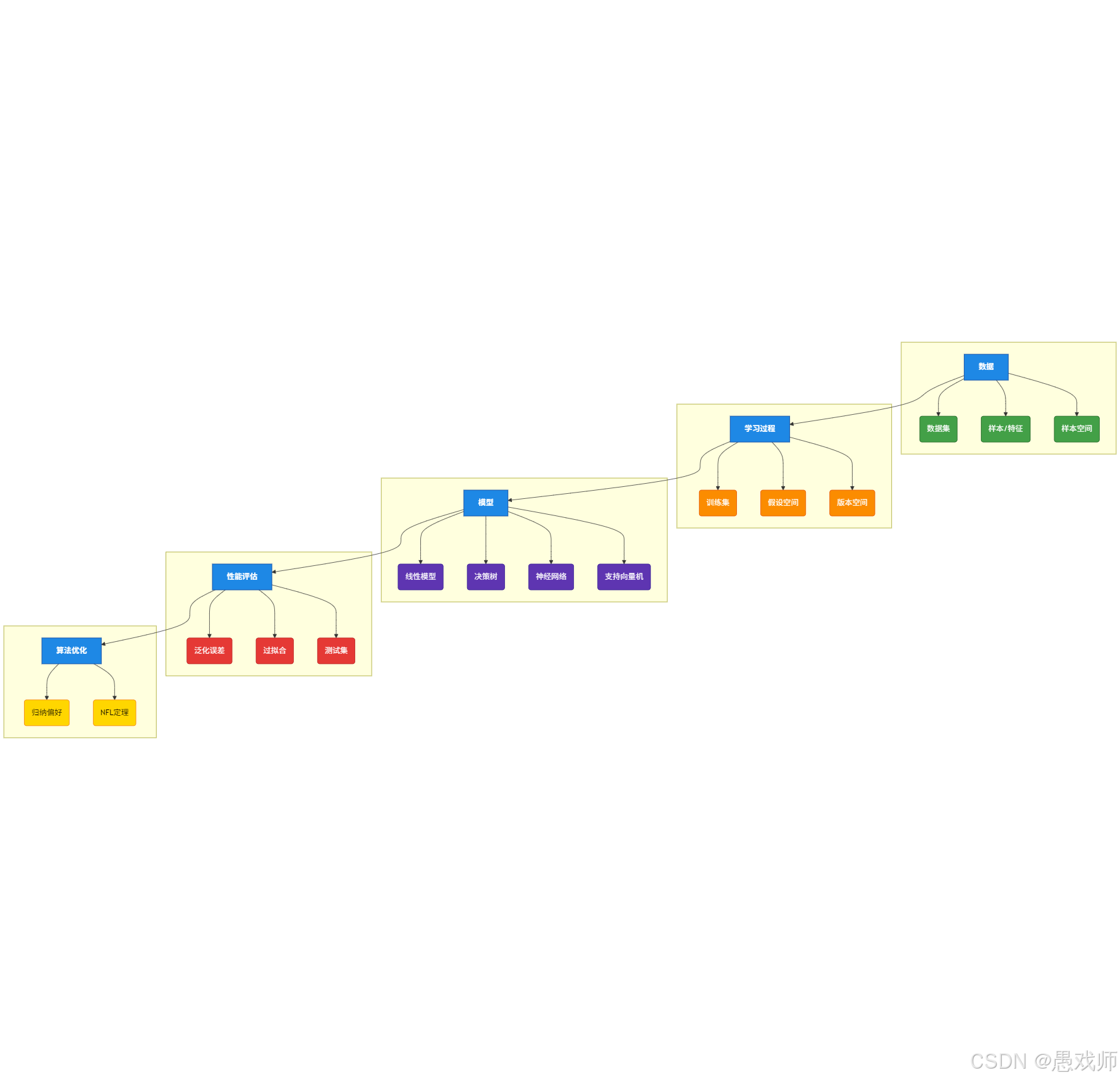?2、核心術語

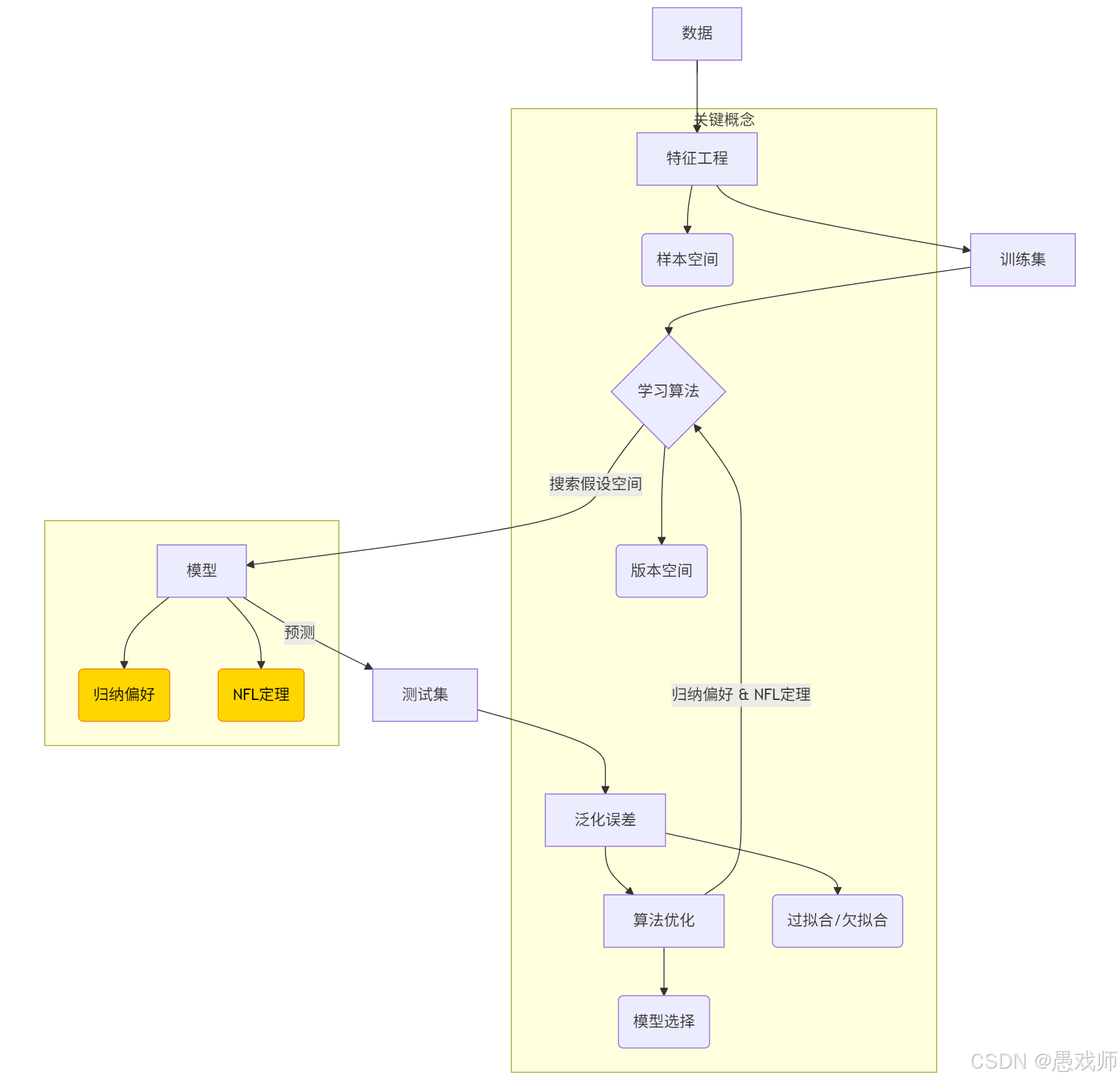
2.1、基礎概念與數據術語

機器學習（Machine Learning, ML）
通過計算手段利用數據（經驗）改善系統性能的學科，核心是從數據中生成模型的學習算法。
示例：用歷史房價數據訓練模型預測新房價。
數據集（Data Set）
多條記錄組成的集合，每條記錄描述一個對象或事件。
示例：1000條西瓜的{色澤, 根蒂, 敲聲, 標簽}記錄。
樣本/示例（Sample/Instance）
數據集中的單條記錄（如一條西瓜數據）。
樣例（Example）：帶標記（Label）的樣本（如標注"好瓜"的西瓜數據）。
特征/屬性（Feature/Attribute）
描述樣本的維度（如西瓜的"色澤"），其取值稱屬性值（Attribute Value）（如"青綠"）。
樣本空間（Sample Space）
所有特征張成的多維空間，每個樣本是空間中的一個點（即特征向量）。
示例：用[色澤, 根蒂, 敲聲]構建三維空間，每個西瓜對應一個坐標點。

2.2、學習過程術語

訓練（Training）
從數據中學習模型的過程，核心是通過算法發現數據內在規律。
- 訓練集（Training Set）：用于訓練模型的數據集合（如80%的西瓜數據）
- 訓練樣本（Training Sample）：訓練集中的單條數據記錄（如一條西瓜的{色澤=青綠, 根蒂=蜷縮, 標簽=好瓜}）
  示例：用1000條歷史病例訓練疾病診斷模型
假設（Hypothesis）
模型對數據規律的推測（如“根蒂蜷縮的西瓜是好瓜”），目標是逼近真相（Ground-Truth）（客觀規律）。
模型是假設的形式化表達，學習本質是尋找最佳假設
標記（Label）
樣本的預測目標值（監督學習的核心），又稱標簽。
- 分類任務：離散值（如“好瓜/壞瓜”）
- 回歸任務：連續值（如西瓜價格15.6元）
  帶標記的樣本稱為?樣例（Example）
假設空間（Hypothesis Space）
所有可能假設的集合，反映問題的求解范圍。
- 示例：西瓜分類問題中，所有由“色澤/根蒂/敲聲”組合構成的判斷規則
- 數學表達：若特征有3個二值屬性，假設空間大小為?223=256223=256?種可能規則
版本空間（Version Space）
假設空間中與訓練集一致的假設子集（即符合所有訓練樣本的假設）。

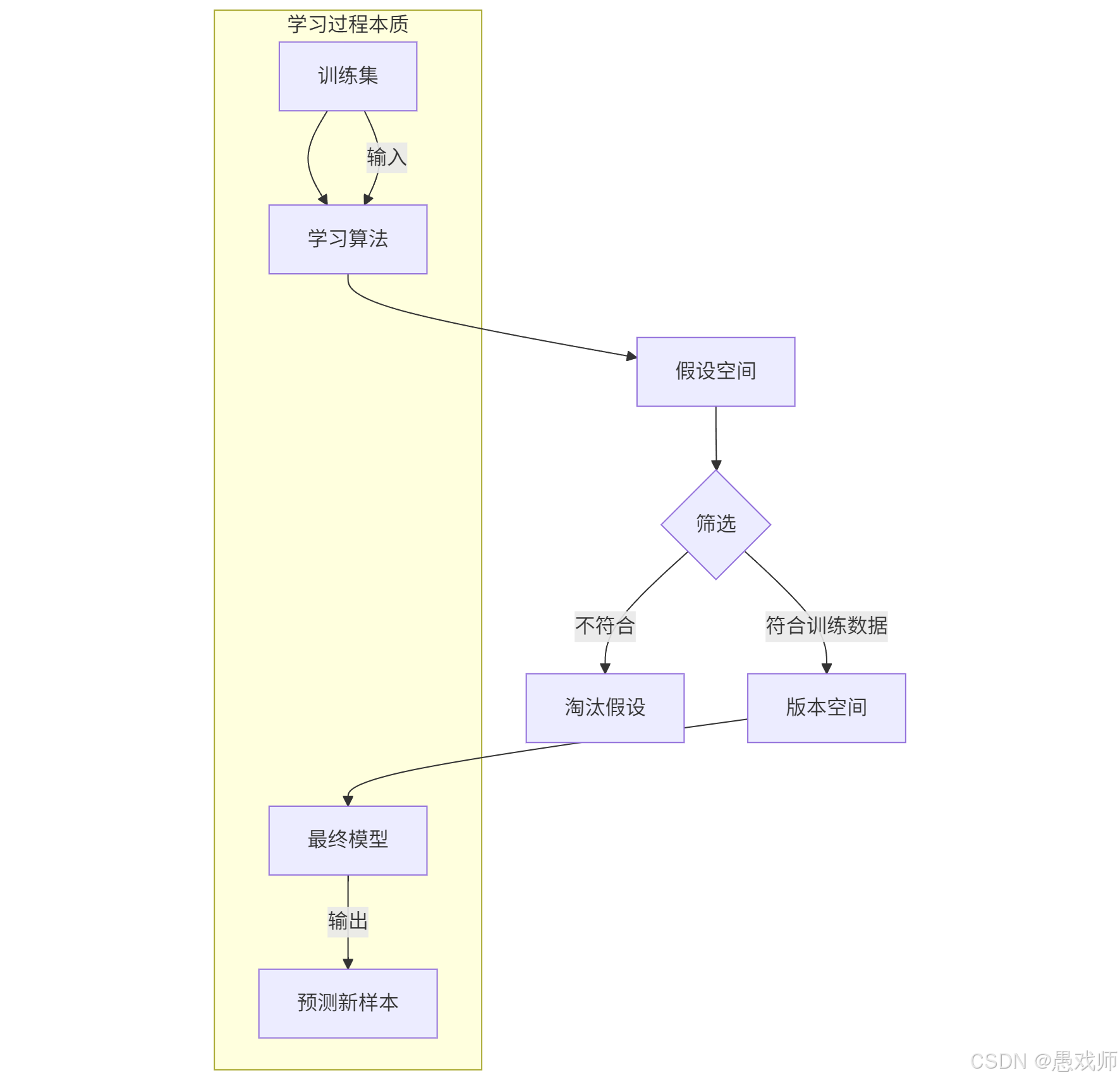
舉個例子：（西瓜分類）

訓練集
- 樣本1：{色澤=青綠, 根蒂=蜷縮, 敲聲=濁響, 標簽=好瓜}
- 樣本2：{色澤=烏黑, 根蒂=稍蜷, 敲聲=沉悶, 標簽=壞瓜}
假設空間
- 假設1：根蒂=蜷縮 → 好瓜
- 假設2：色澤=青綠 AND 敲聲=濁響 → 好瓜
版本空間生成
- 若假設1能正確分類所有訓練樣本 → 進入版本空間
- 若假設2將樣本2誤分類 → 被淘汰
最終模型
從版本空間中根據歸納偏好選擇最優假設（如選擇最簡規則：“根蒂=蜷縮 → 好瓜”）

核心價值：版本空間縮小了搜索范圍，使學習算法能高效找到可行解，但最終模型選擇依賴算法偏好（如奧卡姆剃刀原則優先選擇簡單假設）。

2.3、性能評估術語

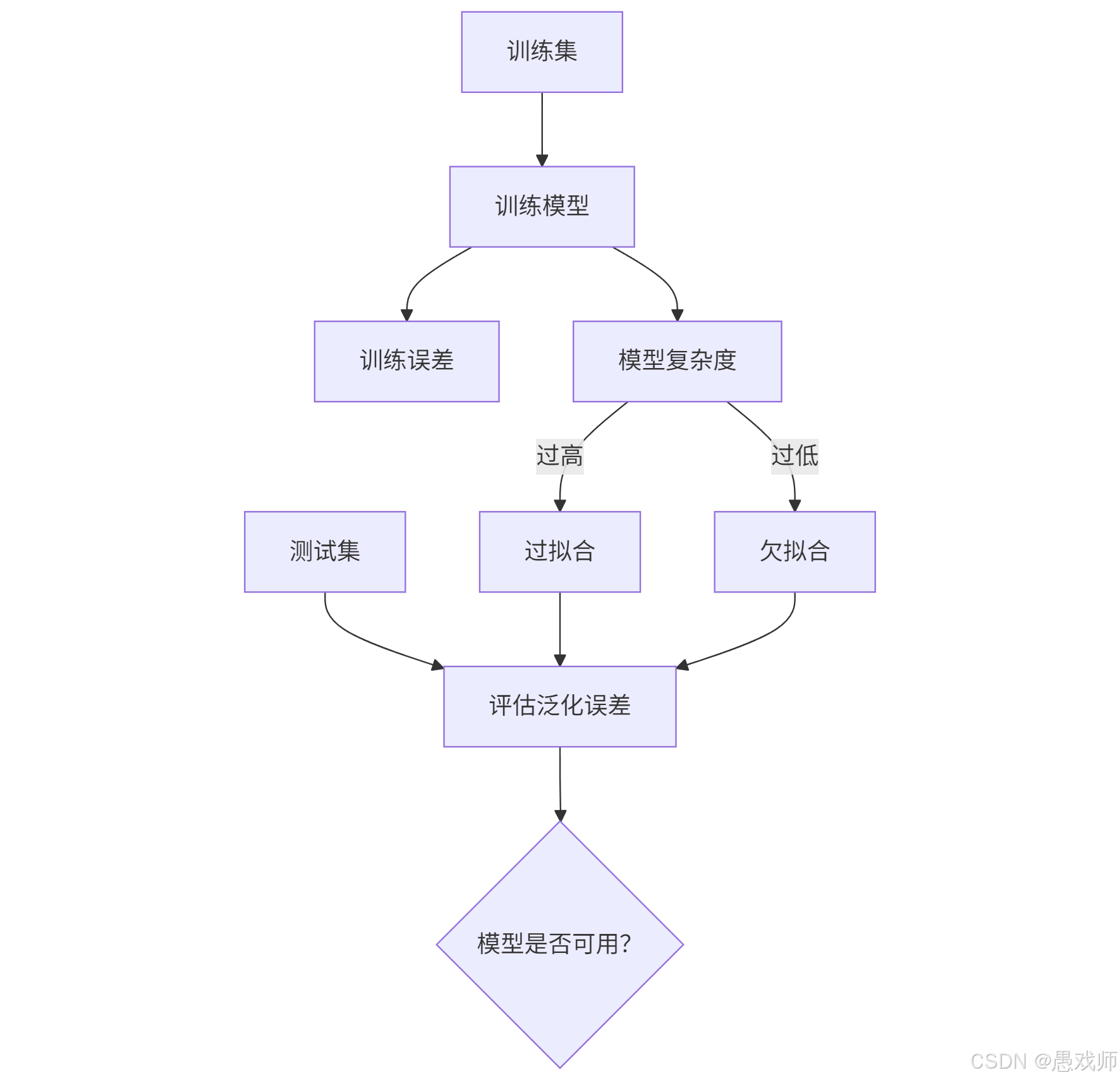
1.?誤差（Error）

定義：模型預測結果與真實值之間的差異。
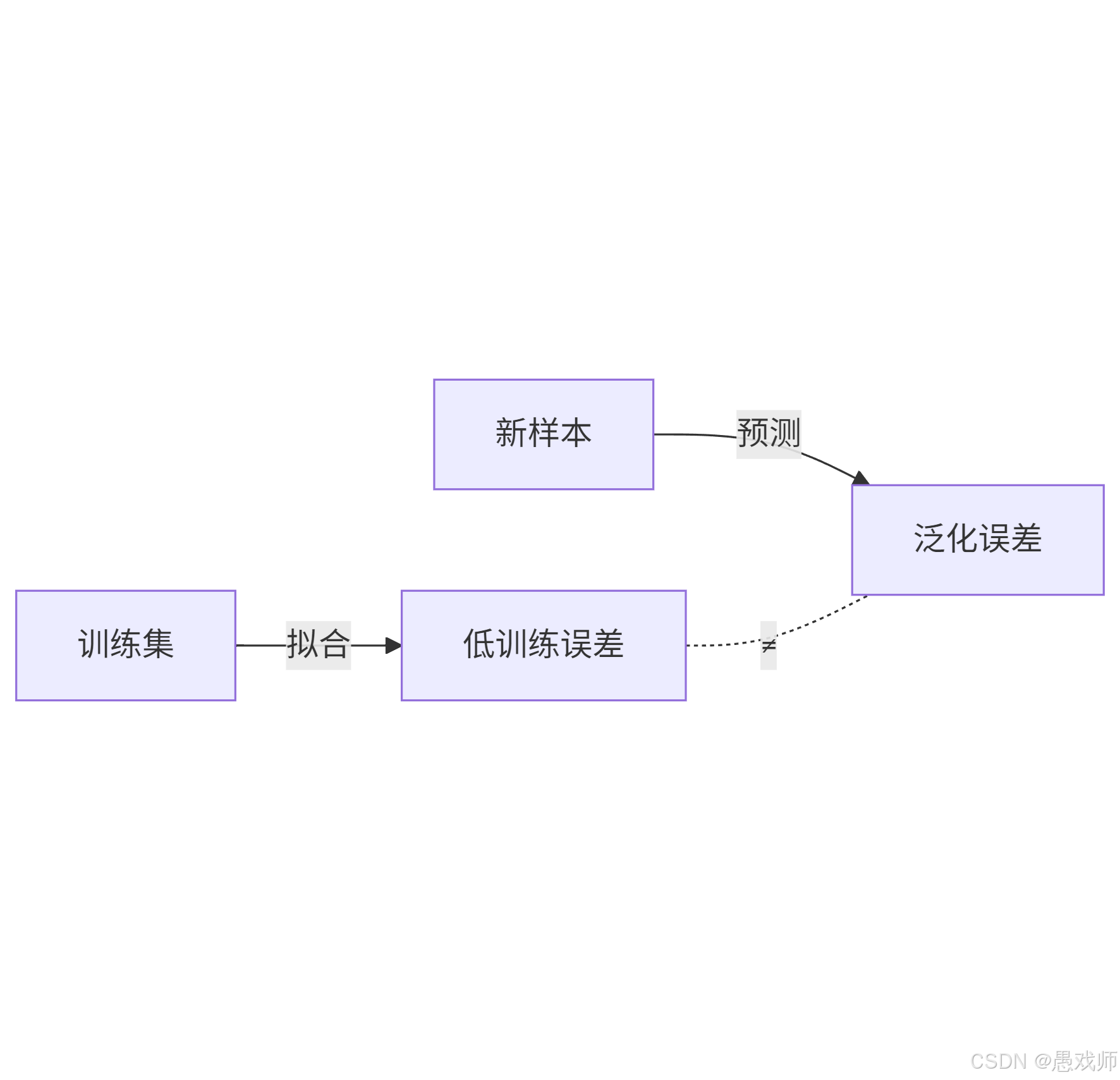
訓練誤差（Training Error）：模型在訓練集上的誤差（反映模型對已知數據的擬合程度）。
泛化誤差（Generalization Error）：模型在新樣本上的誤差（反映模型的實際應用能力，核心優化目標）。

2.?泛化（Generalization）

定義：模型對未見過的數據的適應能力。
核心目標：最小化泛化誤差（而非訓練誤差）。
示例：背熟100道題得滿分（訓練誤差=0），但考試遇到新題不及格（泛化誤差高）→ 泛化失敗。?

3.?過擬合（Overfitting） vs 欠擬合（Underfitting）

現象	本質原因	表現	解決方案
過擬合	模型過度復雜，擬合了訓練數據中的噪聲	訓練誤差極低，泛化誤差高	正則化、增加數據量、簡化模型
欠擬合	模型過于簡單，未捕捉數據規律	訓練誤差和泛化誤差均高	增加模型復雜度、特征工程

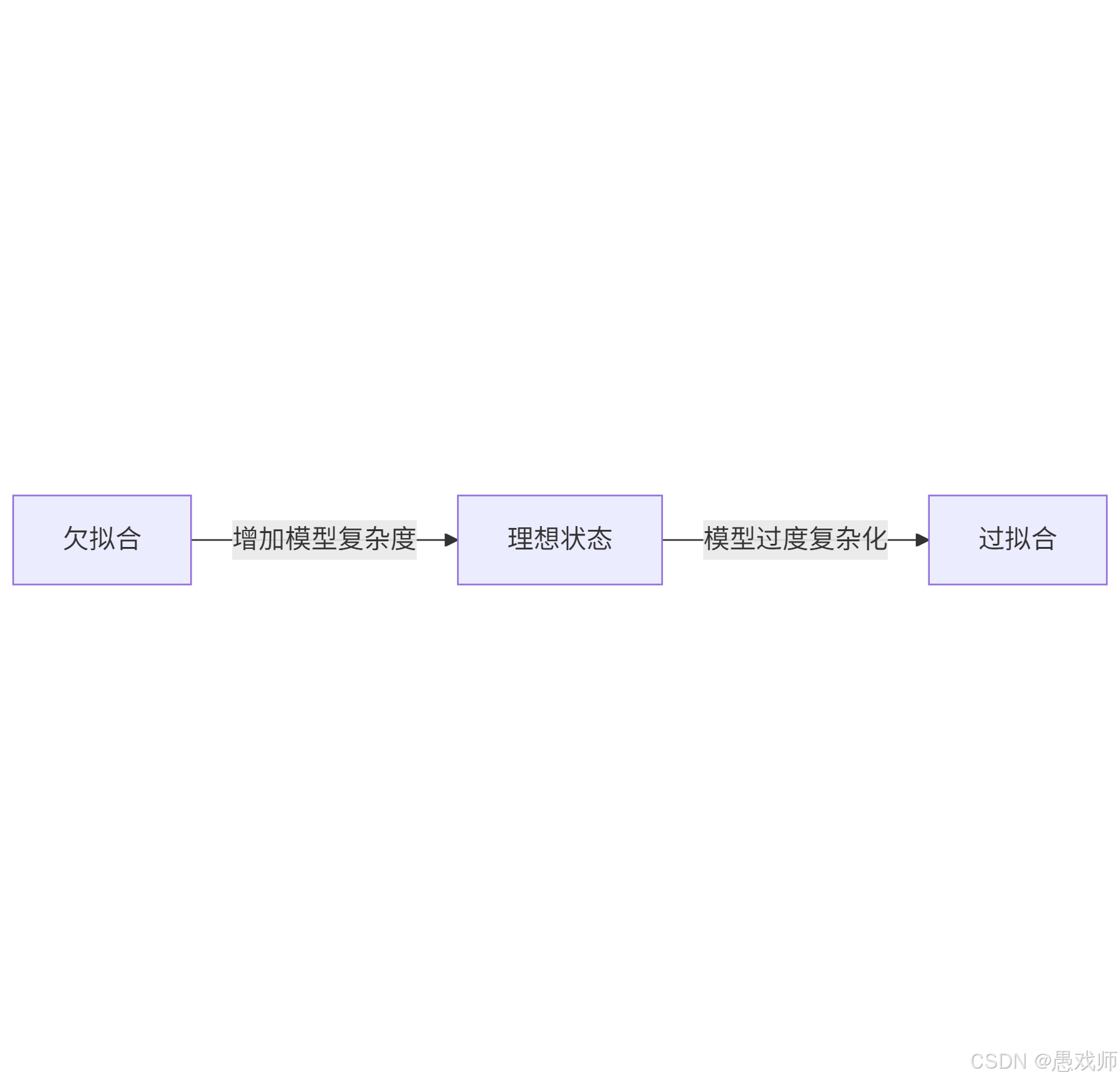
4.?測試集（Testing Set）

定義：用于最終評估模型泛化性能的獨立數據集，必須與訓練集完全互斥（無重疊樣本）。
為什么需要？：防止模型通過“死記硬背”訓練數據獲得虛假高精度。
實踐規則：
劃分比例：常用 70% 訓練集 / 30% 測試集
嚴格隔離：測試集樣本絕不能參與訓練過程
反例：若用全部數據訓練和測試，模型可能100%準確但實際無法預測新樣本。

2.4、算法哲學術語

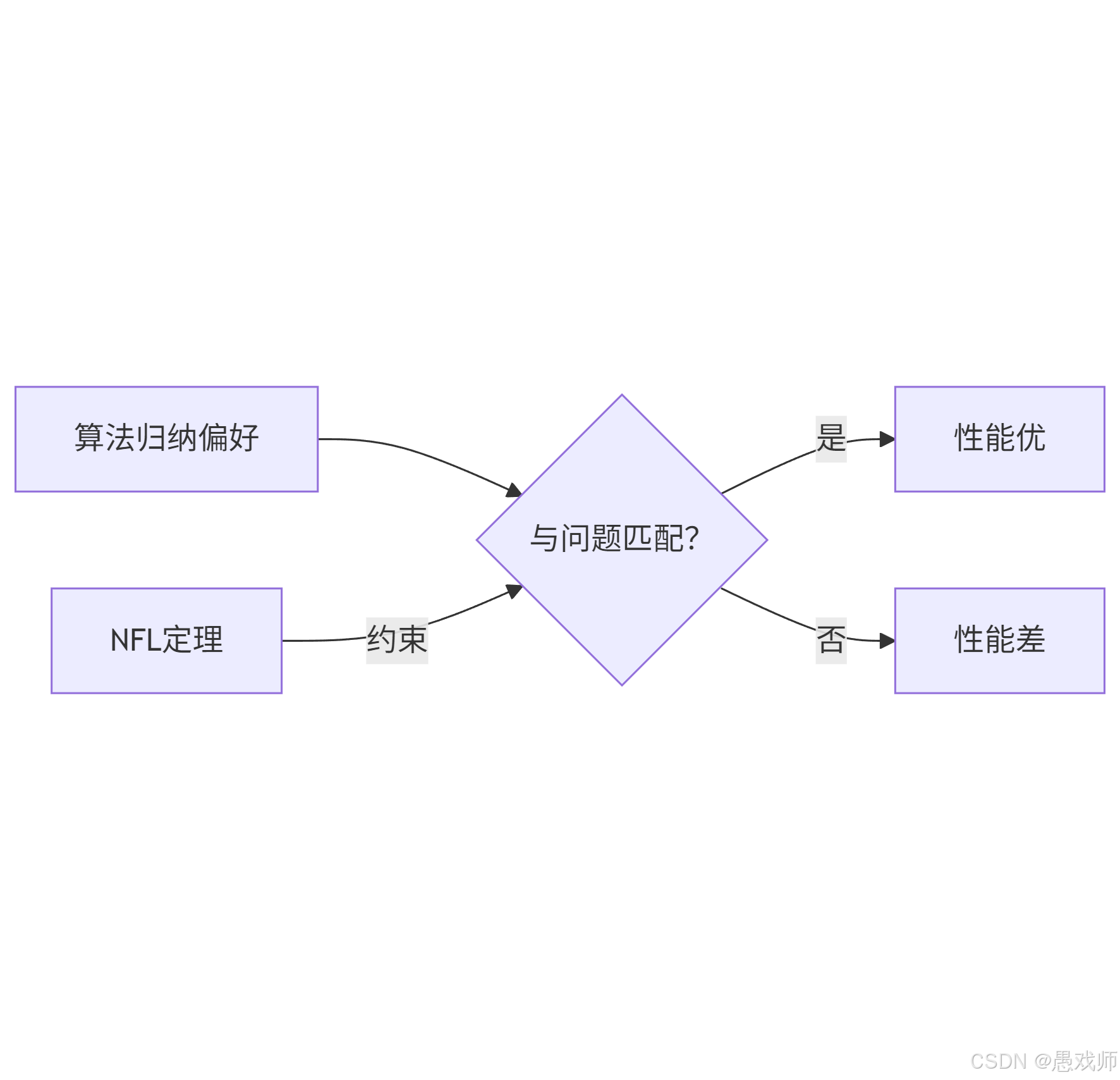
歸納偏好（Inductive Bias）
算法對特定假設的先天偏好（如決策樹偏好"信息增益高的特征"）。
NFL 定理（No Free Lunch Theorem）
核心：沒有萬能最優算法！脫離具體問題，所有算法期望性能相同。
啟示：為圖像識別選CNN，為表格數據選決策樹。

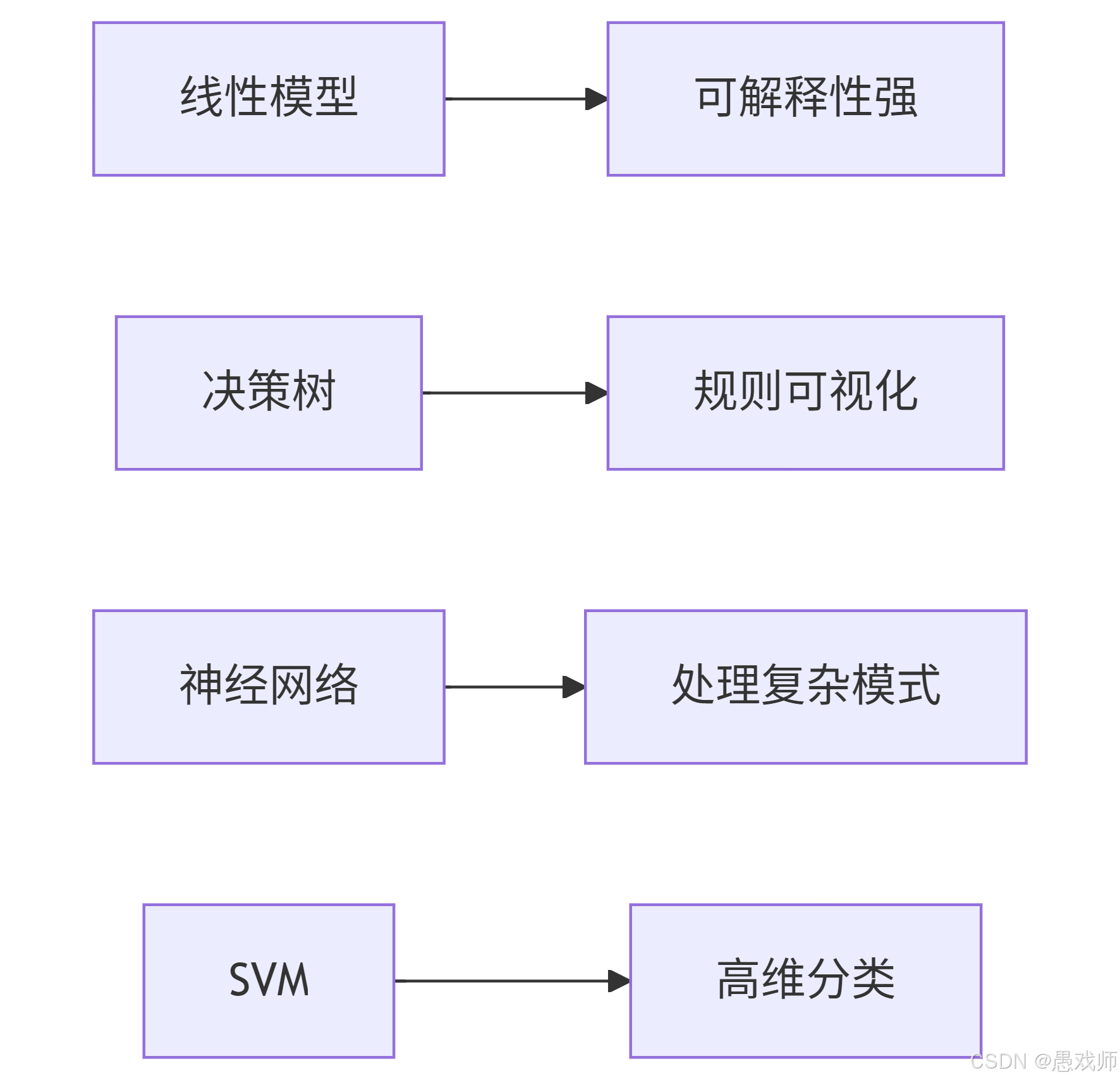
2.5、經典算法術語

Algorithm	Key Concept	Core Mechanism
線性模型（Linear Model）	$f(x)=w^{T}x+b$	Interpretable linear combinations
決策樹（Decision Tree）	Tree-structured attribute partitioning (e.g., color → stem → sound)	Splitting criteria (信息增益/Gini)
神經網絡（Neural Network）	Layered nonlinear transformations	反向傳播（Backpropagation, BP）
支持向量機（Support Vector Machine, SVM）	Maximize-margin hyperplane	核技巧（Kernel Trick）/支持向量（Support Vectors）

?3.歸納偏好與NFL定理

“沒有最好的算法，只有最匹配問題的算法”
—— 通過分析數據分布、目標函數、誤差容忍度，選擇偏好與問題對齊的模型。?

3.1、歸納偏好（Inductive Bias）

1. 核心內容

定義：算法對特定假設的固有偏好（如“簡單模型優先”），是模型從版本空間中選擇唯一解的必要條件。
必要性：
若無偏好，當多個假設與訓練集一致時（如西瓜分類中“好瓜=根蒂蜷縮”和“好瓜=根蒂蜷縮且敲聲濁響”），算法無法穩定預測新樣本。
表現形式：
- 奧卡姆剃刀：偏好更簡單的假設（如決策樹剪枝）。
- 特征偏好：某些算法更關注特定特征（如SVM偏好間隔最大的分類面）。

2. 數學原理

假設空間搜索約束：

3.2、NFL定理（No Free Lunch Theorem）

1. 核心內容

核心結論：
在所有可能問題分布均勻的假設下，任何算法的期望性能相同。
即：若算法A在問題集?F1??上優于B，則必存在問題集?F2?使B優于A。
脫離具體問題談“最優算法”無意義，需匹配問題特性（如數據分布、目標函數）。

2. 數學原理

目標函數均勻分布假設：
設真實目標函數?f均勻分布在所有可能函數空間?F?中。
期望誤差推導：

證明核心：對所有?f?求和后，算法間的差異被抵消。

3.3、兩者關聯

偏好決定性能邊界：
歸納偏好是算法“個性”，而NFL定理證明其性能高度依賴問題場景。

3.4、NFL定理應用實例

案例：西瓜分類中的算法選擇

場景1：真實規律為“根蒂蜷縮→好瓜”
- 算法A：偏好“根蒂”特征（如決策樹按信息增益優先選擇根蒂）
  → 高準確率
- 算法B：偏好“敲聲”特征（如人為設定特征權重）
  → 低準確率
場景2：真實規律變為“敲聲濁響→好瓜”
- 算法A：因錯誤偏好 → 準確率下降
- 算法B：與問題匹配 → 準確率上升
NFL生效：
若均勻隨機出現兩種場景，算法A和B的長期平均準確率相同。

實際項目應用建議：

問題分析優先：
- 考察數據分布（如特征相關性、噪聲水平）
- 明確任務目標（如分類精度 vs. 模型解釋性）

算法匹配策略：

問題特性	推薦算法	原因
特征間線性可分離	SVM/線性模型	偏好最大間隔/線性關系
高維非結構化數據	神經網絡	偏好多層非線性特征提取
需可解釋性	決策樹	偏好規則簡單性

3.5、關鍵問題解答

Q1: 算法A在部分問題優于B，在其他問題是否必然更差（僅個人不成熟的經驗）

不一定。NFL定理僅保證在所有問題均勻分布時，A和B的平均性能相同。
實際中：若現實問題分布不均勻（如圖像識別任務遠多于語音任務），某些算法可能長期占優。

Q2: 如何將NFL定理應用于實際項目（僅個人不成熟的經驗）

“萬能算法”是幻想：
測試新問題時，至少比較3種不同偏好的算法（如樹模型、神經網絡、SVM）。
問題拆解匹配偏好：
- 子任務1（特征選擇）：用偏好稀疏性的Lasso回歸
- 子任務2（模式識別）：用偏好復雜邊界的神經網絡
動態算法切換：
監控數據分布漂移（如用戶行為變化），當原有算法性能下降時，切換至匹配新分布的算法。

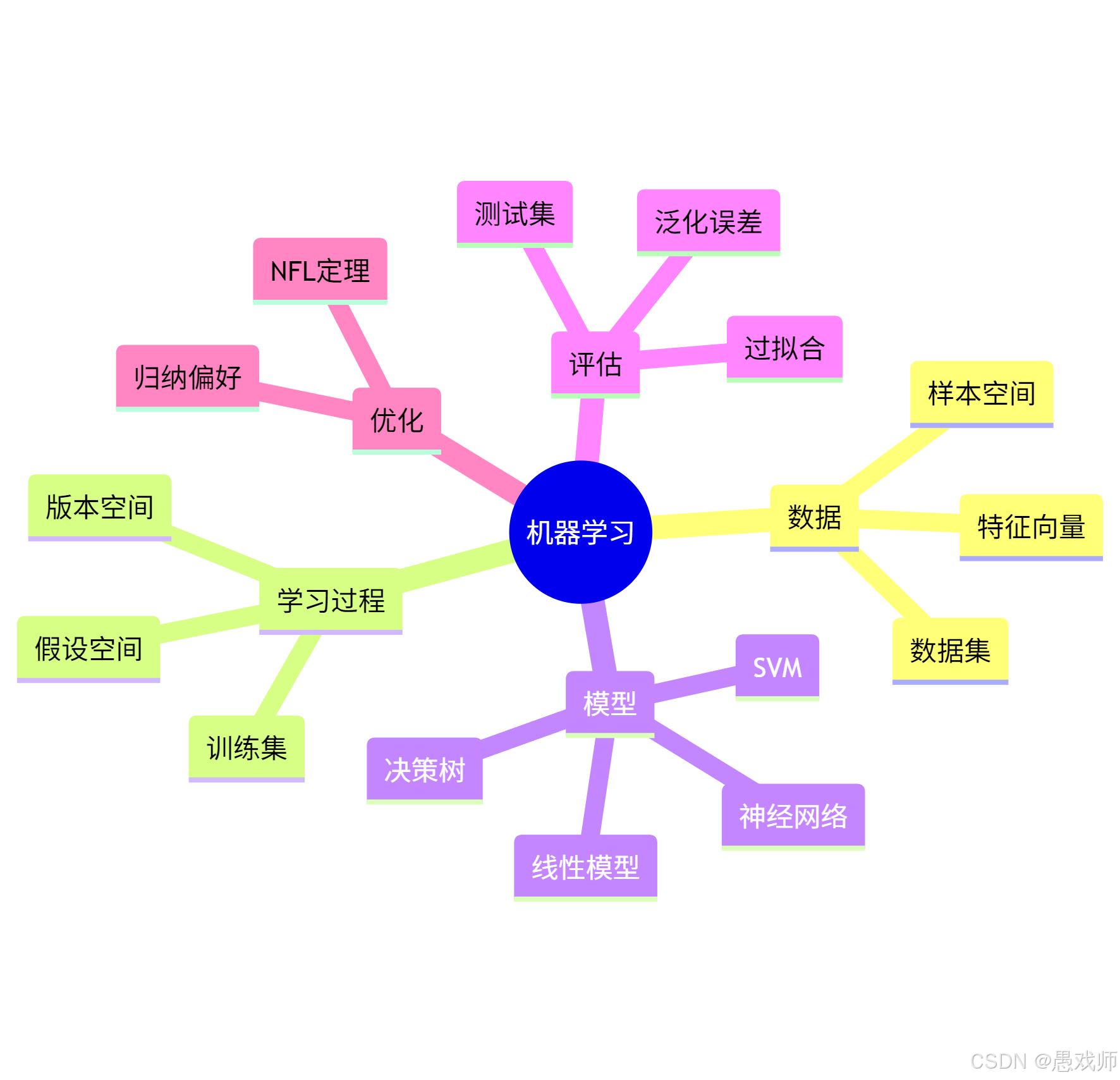
4、一圖小結

機器學習是?"數據→學習→模型→評估→優化"?的閉環系統，NFL定理要求我們根據問題特性動態調整算法偏好。?

5、模型評估與選擇?

5.1、過擬合/欠擬合

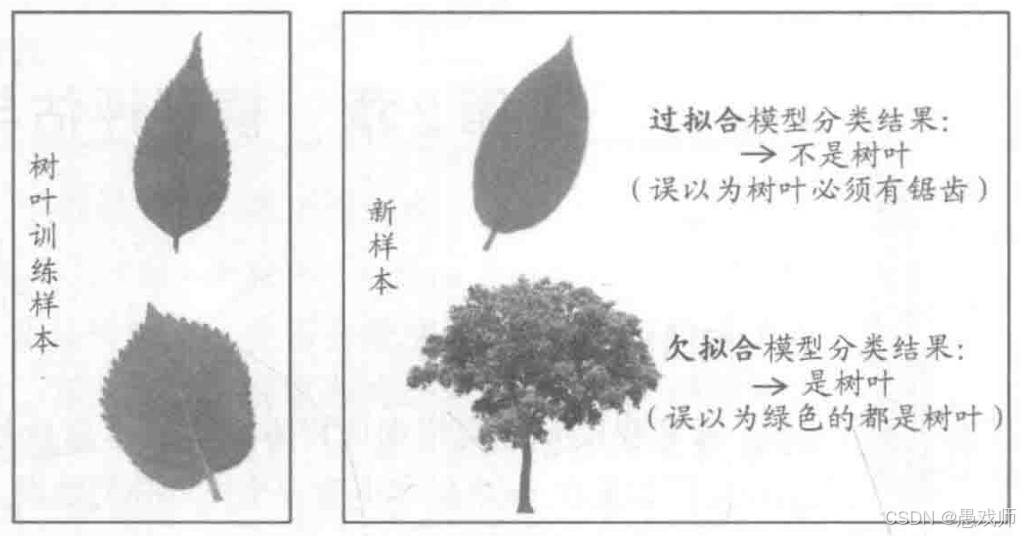引用自西瓜書?

5.1.1、過擬合與欠擬合核心對比?

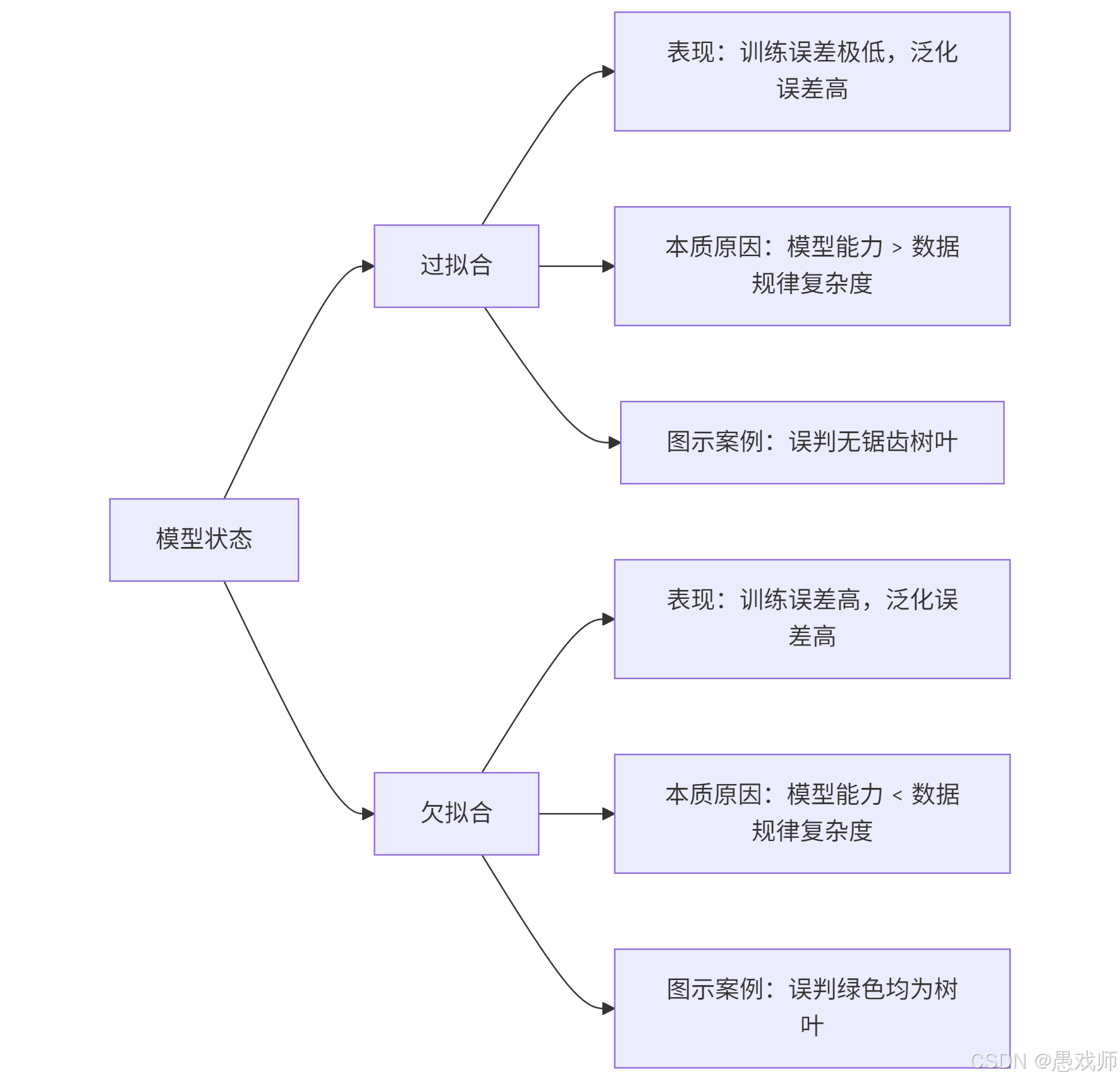?5.1.2、直觀解析

過擬合

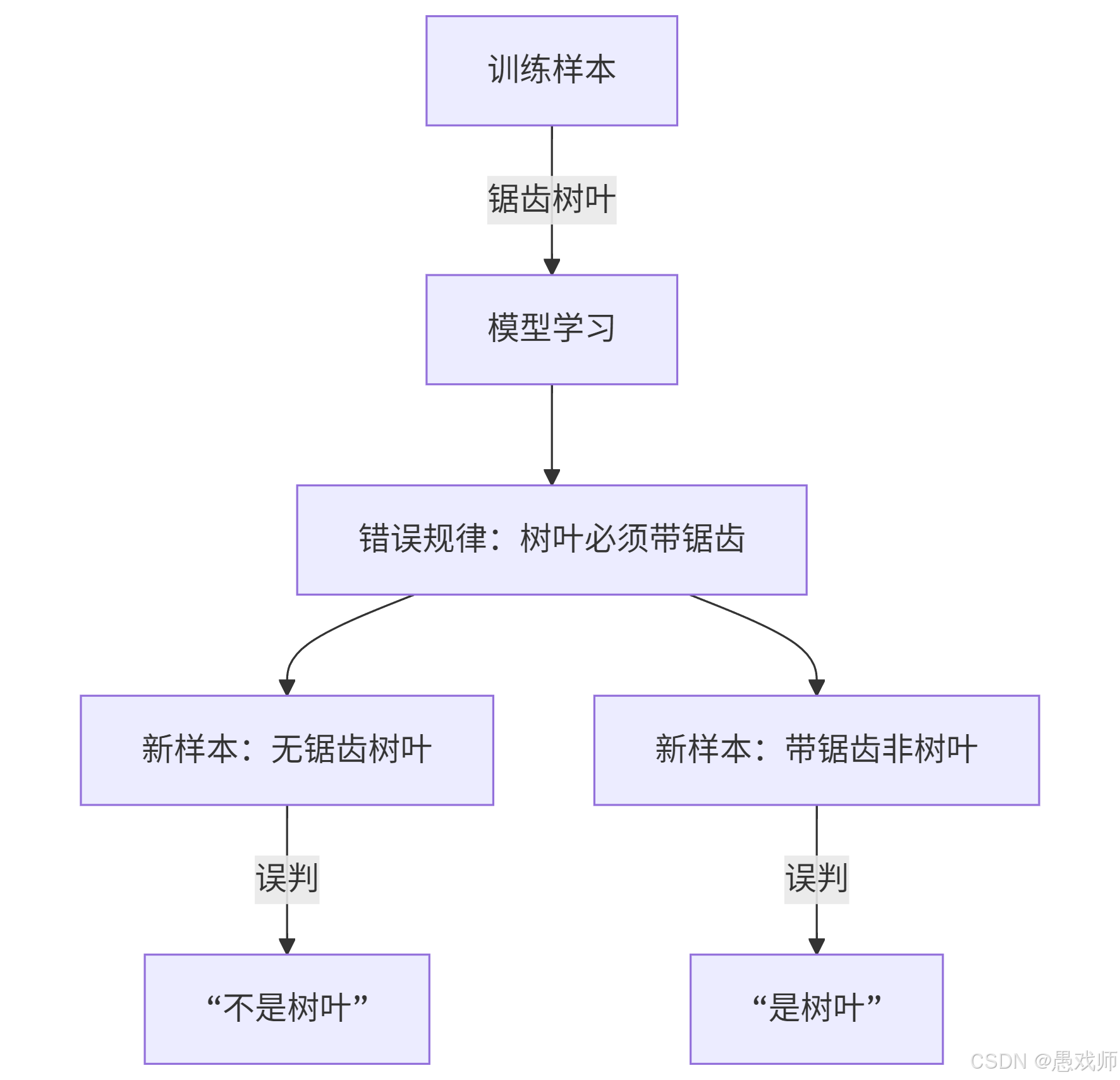
關鍵錯誤：將訓練樣本的偶然特性（鋸齒）當作普遍規律
現實案例：人臉識別模型將"戴眼鏡"作為必要特征，導致無法識別不戴眼鏡的用戶

欠擬合?

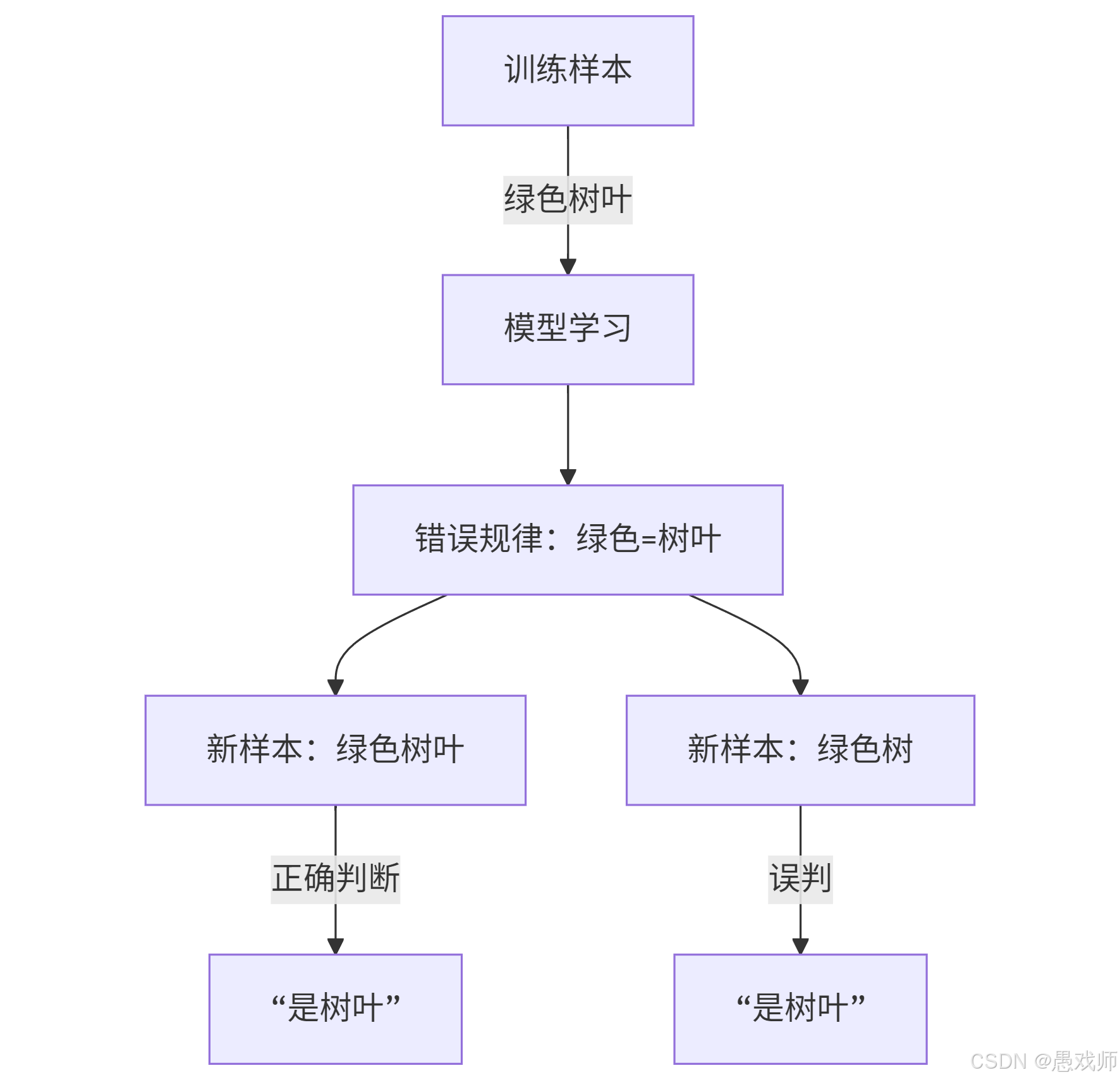
關鍵錯誤：未學習到形狀、紋理等關鍵特征
現實案例：垃圾郵件過濾僅基于關鍵詞"免費"，誤判重要郵件

對照表

維度	過擬合	欠擬合
模型能力	過于復雜（如深層神經網絡）	過于簡單（如線性回歸）
數據匹配度	模型復雜度 > 真實規律復雜度	模型復雜度 < 真實規律復雜度
典型場景	小樣本訓練復雜模型	復雜問題用簡單模型
解決方案	1. 增加訓練數據量 2. 正則化(L1/L2) 3. 降低模型復雜度 4. Dropout(神經網絡)	1. 增加模型復雜度 2. 特征工程 3. 延長訓練時間 4. 減少正則化強度

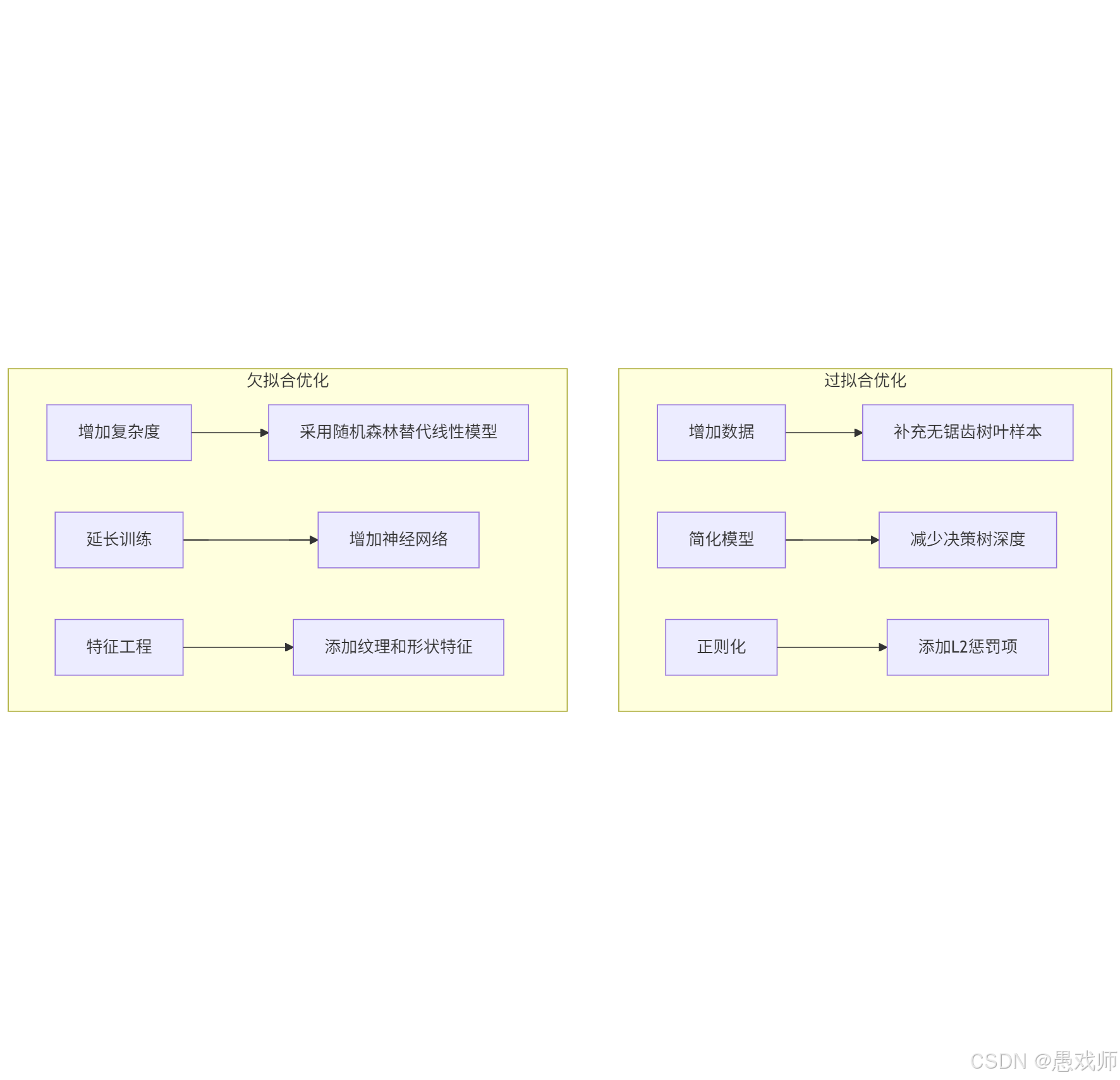
?5.2、模型評估方法

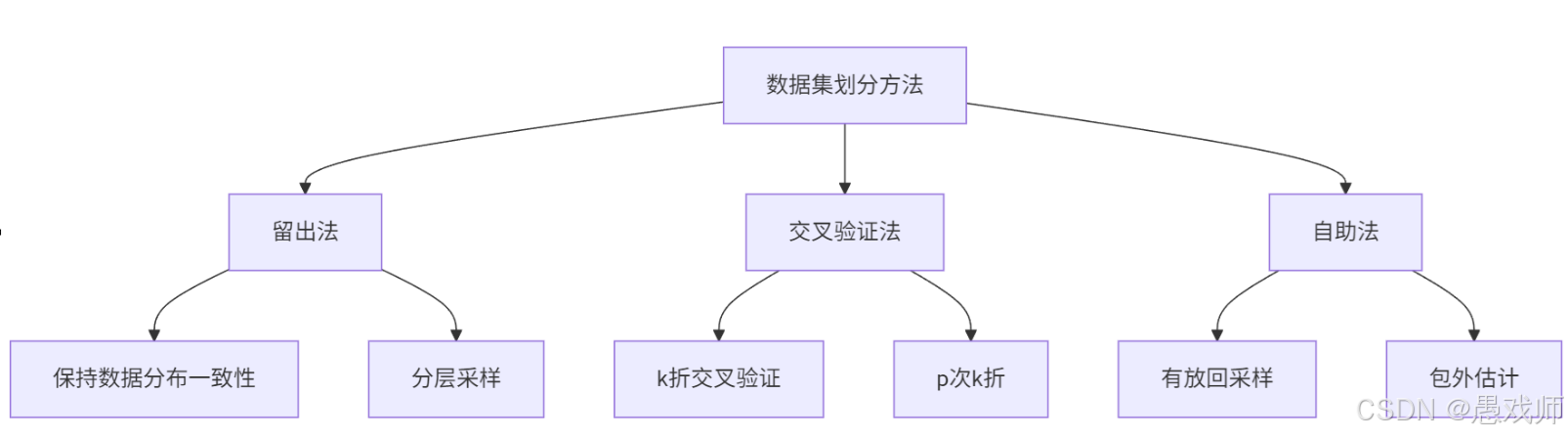
?5.2.1、留出法（hold-out）

核心思想：將數據集?D?劃分為兩個互斥子集，分別作為訓練集?S（用于訓練模型）和測試集?T（用于評估性能），滿足 $D=S\bigcup T and S\bigcap T=\varnothing$ 。
關鍵要求：
- 劃分需保持數據分布一致性（如分類任務采用 “分層采樣” 保持類別比例），避免引入偏差。
- 單次劃分結果不穩定，通常需多次隨機劃分并取平均值（如 100 次劃分后的平均誤差）。
常見比例：訓練集占 2/3~4/5，測試集占 1/5~1/3。

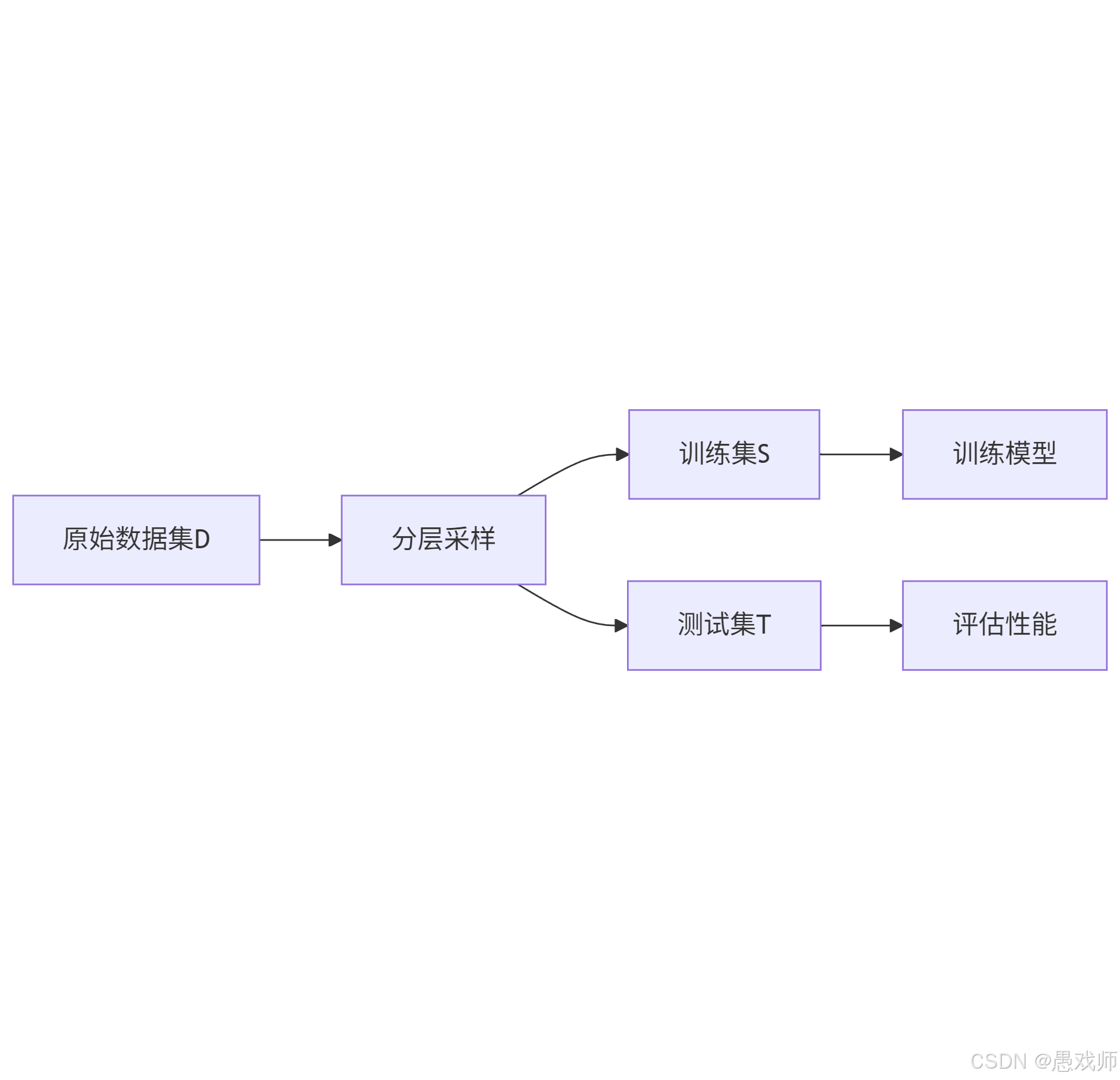
特點：

優點：簡單高效，適合大數據集
缺點：單次劃分結果波動大（需多次隨機劃分取平均）
關鍵要求：
- 分類任務必須分層采樣（保持類別比例）
- 常用比例：訓練集:測試集 = 7:3 或 8:2

5.2.2、?交叉驗證法（Cross Validation）?

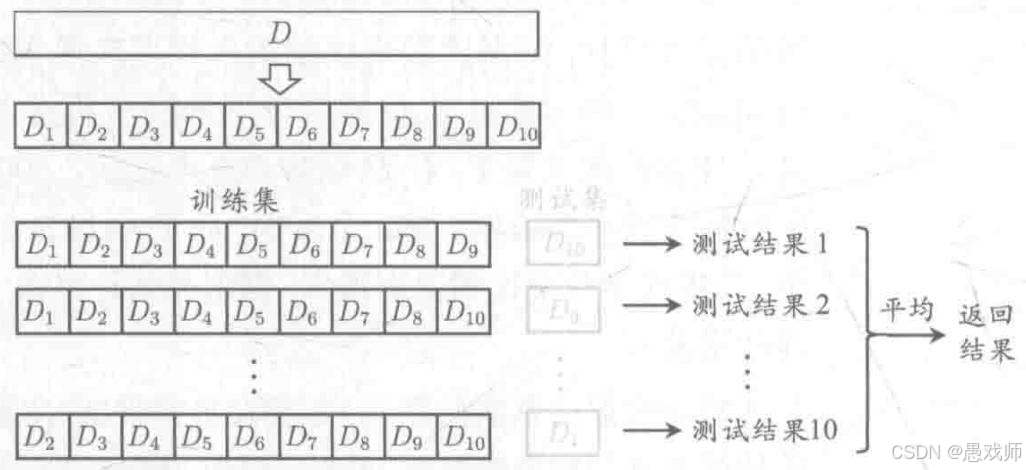?引用自西瓜書?

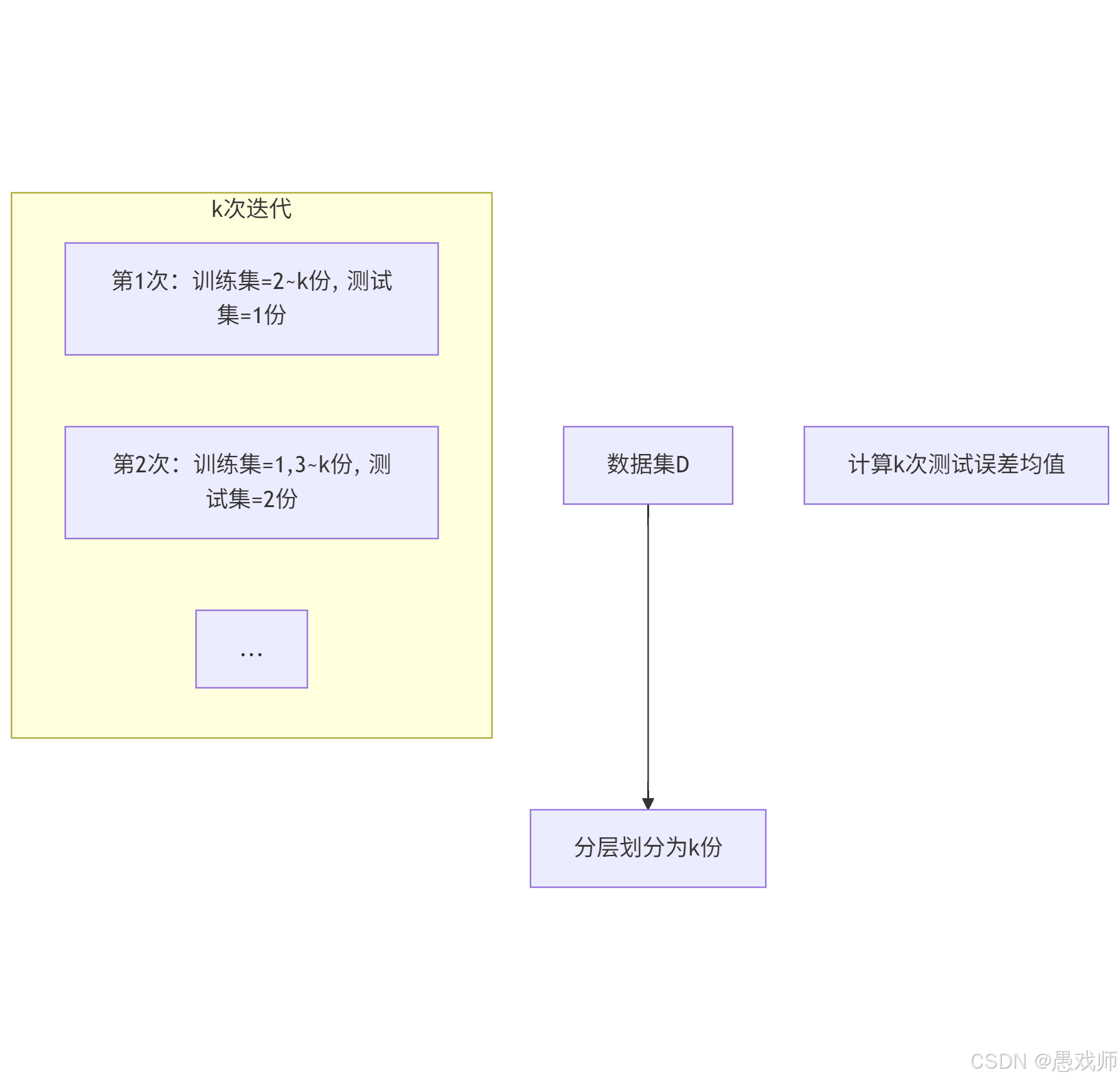
核心思想：將數據集?D?劃分為?k?個大小相似的互斥子集（通過分層采樣生成），每次用 k-1個子集的并集作為訓練集，剩余 1 個子集作為測試集，重復?k?次后取平均誤差，稱為 “k折交叉驗證”。
常用設置：
- k=10（最常用，稱為 10 折交叉驗證）。
- 為進一步提高穩定性，可采用 “p次k折交叉驗證”（如 10 次 10 折交叉驗證）。
特例：留一法（LOO）：
- 當 k=m（m為樣本數）時，每次留 1 個樣本作為測試集，評估結果準確但計算開銷極大（需訓練m個模型）。

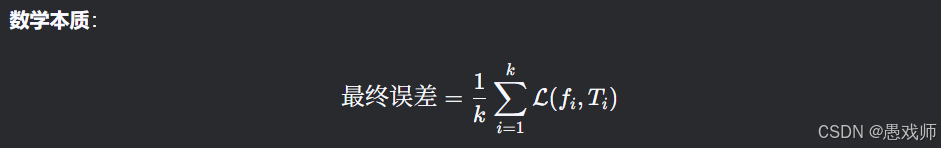
優勢：

充分利用數據（每個樣本都參與測試）
評估結果更穩定（尤其適合小數據集）

?5.2.3、自助法（Bootstrapping）

我們希望評估的是用 D 訓練出的模型,但在留出法和交叉驗證法中,由于保留了一部分樣本用于測試,因此實際評估的模型所使用的訓練集比 D 小,這必然會引入一些因訓練樣本規模不同而導致的估計偏差,留一法受訓練樣本規模變化的影響較小,但計算復雜度又太高了,有沒有什么辦法可以減少訓練樣本規模不同造成的影響,同時還能比較高效地進行實驗估計呢??
引用自西瓜書?

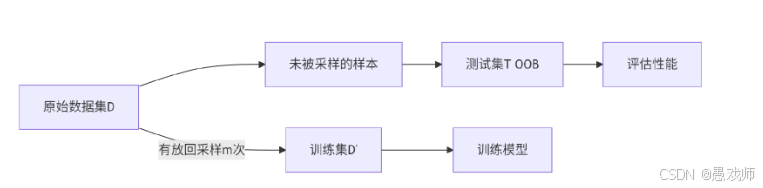
自助采樣流程

初始化：空訓練集?D′=?
循環采樣（重復?m次）：
- 從?D?中隨機選取一個樣本?xi
- 將?xi的拷貝加入?D′
- 將?xi?放回?D?中
生成測試集：
T={x∈D∣x?D′}（包外樣本）

示例：
原始數據集?D={A,B,C}，m=3 次采樣：
第1次：抽到B →?D′={B}
第2次：抽到B →?D′={B,B}
第3次：抽到A →?D′={B,B,A}
測試集?T={C}（未出現的樣本）

數學證明?（字較丑，讀友見諒）

方法特性分析

優勢

特點	說明	應用價值
訓練集規模	(D'= m )（與原始數據集相同）	小數據集也能充分訓練模型
天然劃分	自動生成包外測試集	無需人工劃分數據
多重復用	可重復采樣生成多個D′	集成學習（如Bagging）的基礎
無分布假設	不依賴數據分布特性	適用于任意數據類型

局限

問題	數學解釋	影響
分布偏差	D′中樣本獨立同分布假設被破壞	模型估計可能有偏
樣本相關性	重復樣本導致訓練集樣本間獨立性降低	方差估計不準確
包外樣本偏差	包外樣本非均勻覆蓋（某些樣本從未被測試）	評估結果可能有噪點

?6、性能度量指標

性能度量（performance measure）是衡量學習器泛化能力的評價標準，其選擇需結合具體任務需求。?

6.1、回歸任務性能度量

回歸任務的目標是預測連續值，核心是衡量預測值與真實值的差異，最常用指標為均方誤差。?

均方誤差（Mean Squared Error, MSE）?

實例分析：房價預測

樣本集（單位：萬元）

樣本	真實房價? $y_{i}$	預測房價 $f(x_{i})$	誤差 $f(x_{i})-y^{i}$	平方誤差
1	300	280	-20	400
2	450	460	+10	100
3	500	520	+20	400
4	380	350	-30	900
5	600	620	+20	400

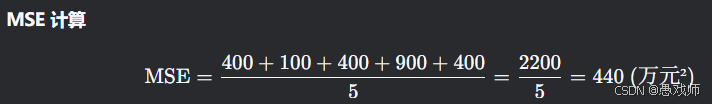
可讀出的結論：

平均偏差：
雖然單樣本誤差有正有負，但平方消除方向影響，反映絕對偏差
異常值敏感：
樣本4的誤差（-30）平方后達900，顯著拉高MSE，?說明模型對低價房預測較差
業務轉換：
- 均方根誤差（RMSE）：440≈21 → 平均預測偏差21萬元
- 相對誤差：21/300=7%（低價房），21/600=3.5%（高價房）

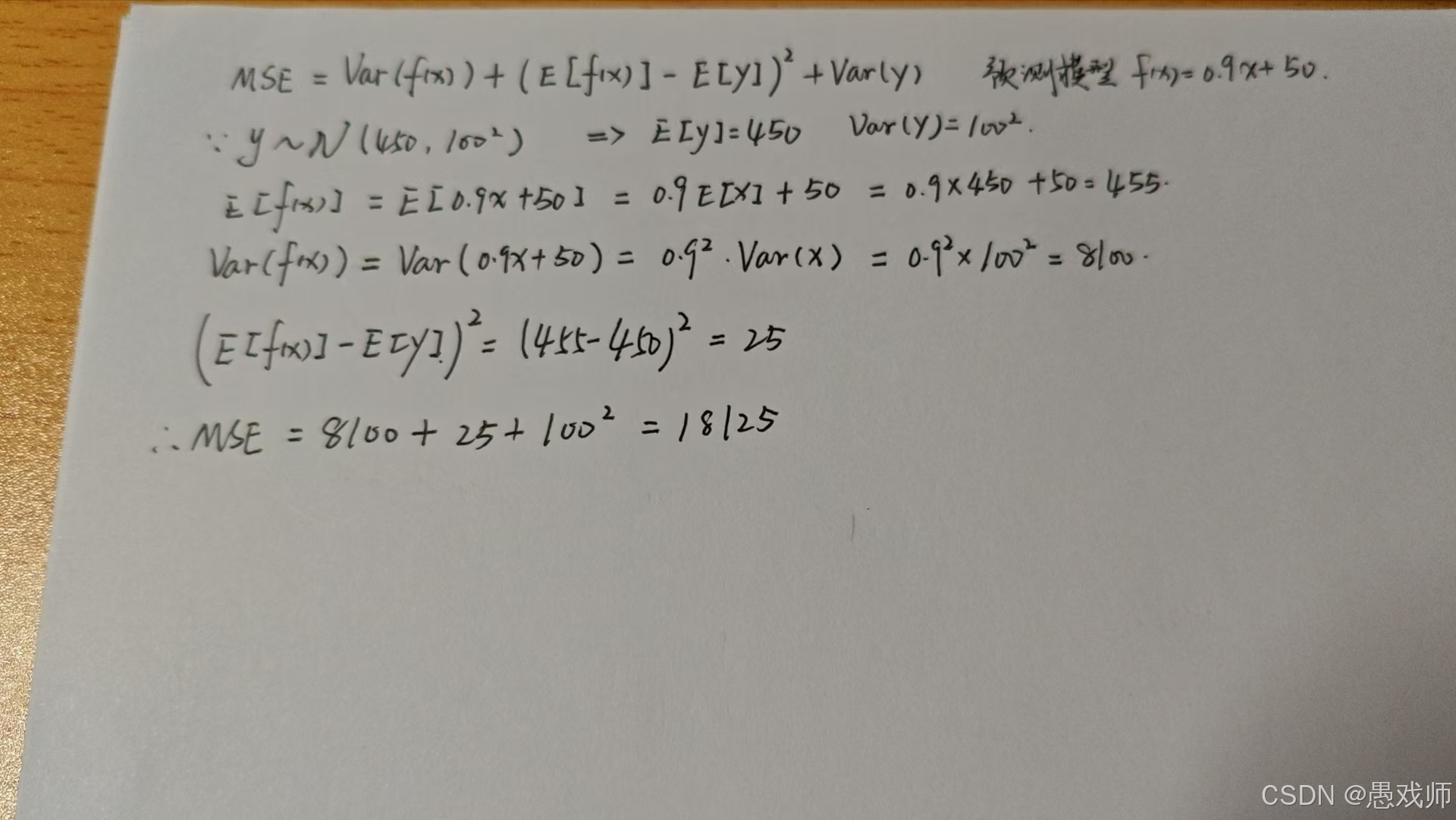
結論：?

1. 模型方差（8,100 ≈ 44.7%）

來源：模型對輸入?x?的波動過于敏感
數學表現：Var(f(x))=0.81×Var(x)

2. 偏差平方（25 ≈ 0.14%）

來源：模型系統性地高估房價 5 萬元
數學表現：E[f(x)]?E[y]=5

3. 數據噪聲（10,000 ≈ 55.2%）

來源：房價本身受市場、地段等不可控因素影響
數學表現：Var(y)=10,000
關鍵認知：
"這是無法通過模型優化的固有誤差，代表預測精度的理論極限"

分解證明：

6.2、分類任務常用性能度量

?分類任務的目標是預測離散類別，需根據任務關注的重點（如 “預測的準確率”“是否漏檢” 等）選擇指標，核心指標包括錯誤率、精度、查準率 - 查全率 - F1、ROC-AUC 等。

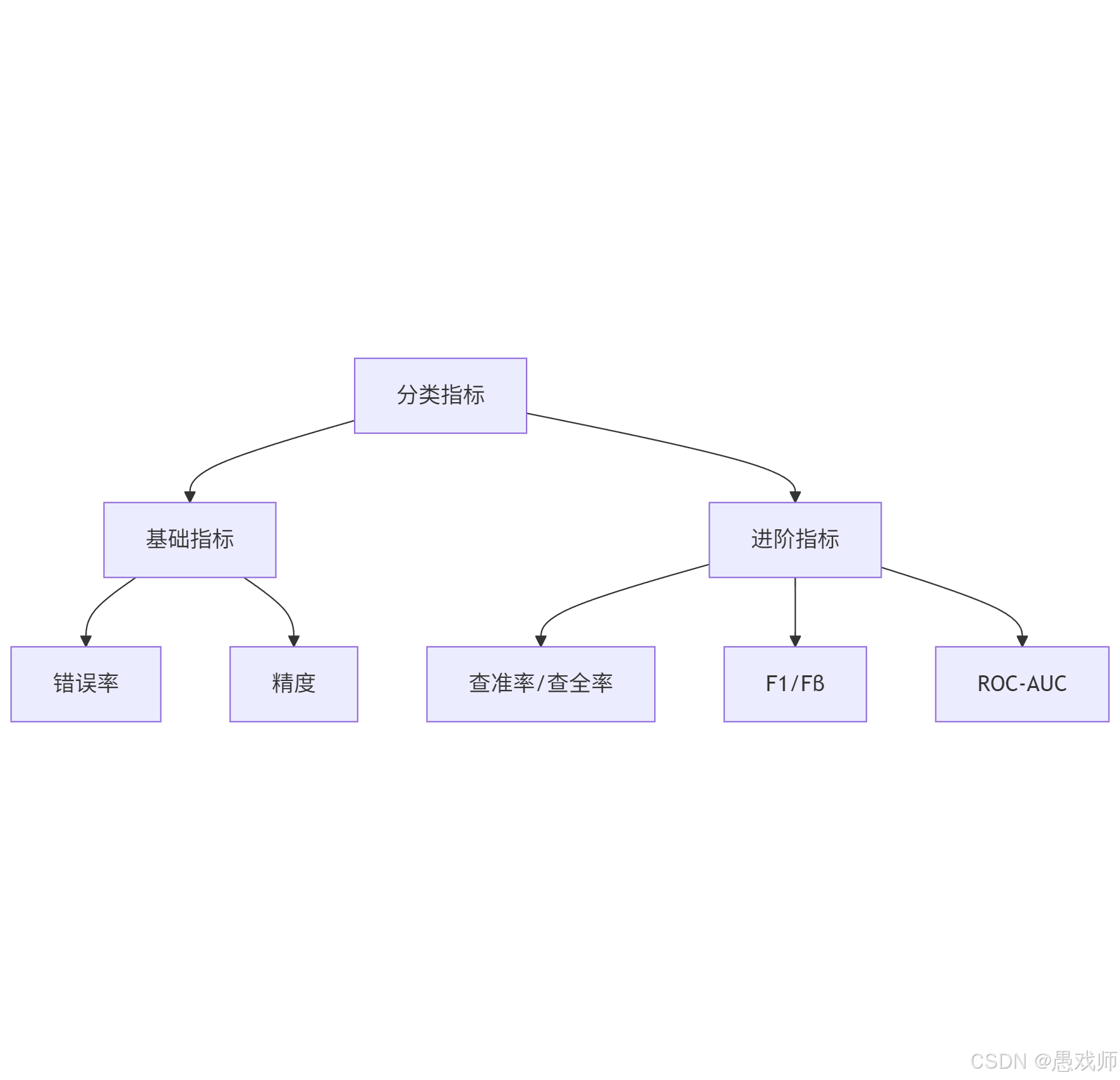
錯誤率與精度

1. 錯誤率（Error Rate）

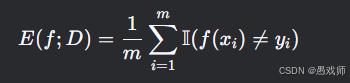
本質：錯分樣本占比
示例：
100個樣本中錯分15個 → 錯誤率=15%

2. 精度（Accuracy）

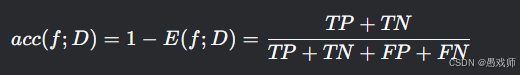
本質：正確分類樣本占比

查準率(P)、查全率(R)與F1

混淆矩陣基礎

	預測正例	預測反例
真實正例	TP	FN
真實反例	FP	TN

查準率（Precision）

意義：預測正例的可靠程度
例：推薦系統預測"用戶會點擊"的準確率

查全率（Recall）

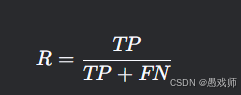
業務意義：正例樣本的覆蓋程度
例：疾病篩查中真正患者的檢出率
優化場景：
- 逃犯檢索（避免漏檢）
- 缺陷產品召回（減少漏召回）

F1 與 Fβ 分數（Precision、Recall）

指標	公式	特點
F1		平衡P與R（調和平均）
Fβ		按需加權（β控制偏好）

β的作用：
- β > 1：更重查全率（如癌癥篩查設β=2）
- β < 1：更重查準率（如推薦系統設β=0.5）

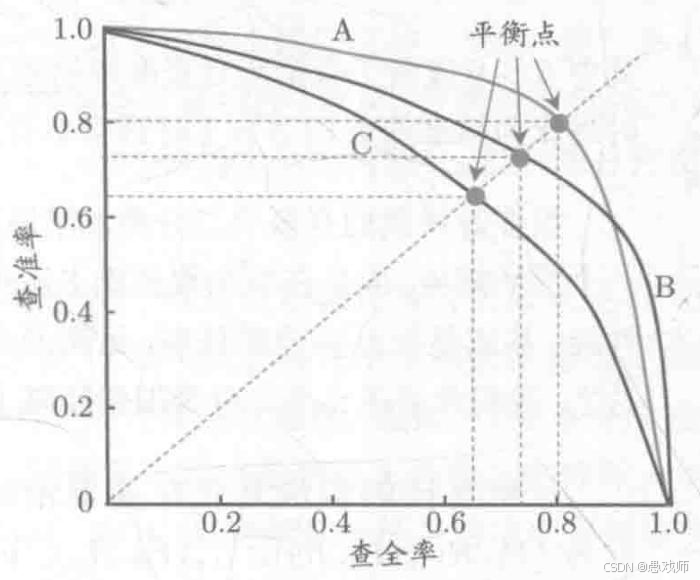引用自西瓜書??

?數學角度分析：

?β值選擇決策矩陣?

實例解析：電商評論情感分析

場景設定

任務：判斷評論是否負面（正例=負面評論）

混淆矩陣：

             預測負面  預測非負面
真實負面       80 (TP)   20 (FN)
真實非負面     30 (FP)   870 (TN)

指標計算

查準率：
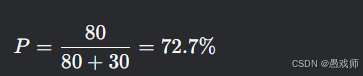
意義：預測為負面的評論中有72.7%真為負面
查全率：
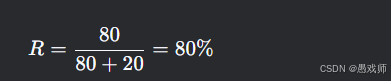
意義：所有負面評論中80%被正確識別
F1分數：

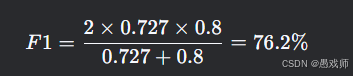
ROC-AUC

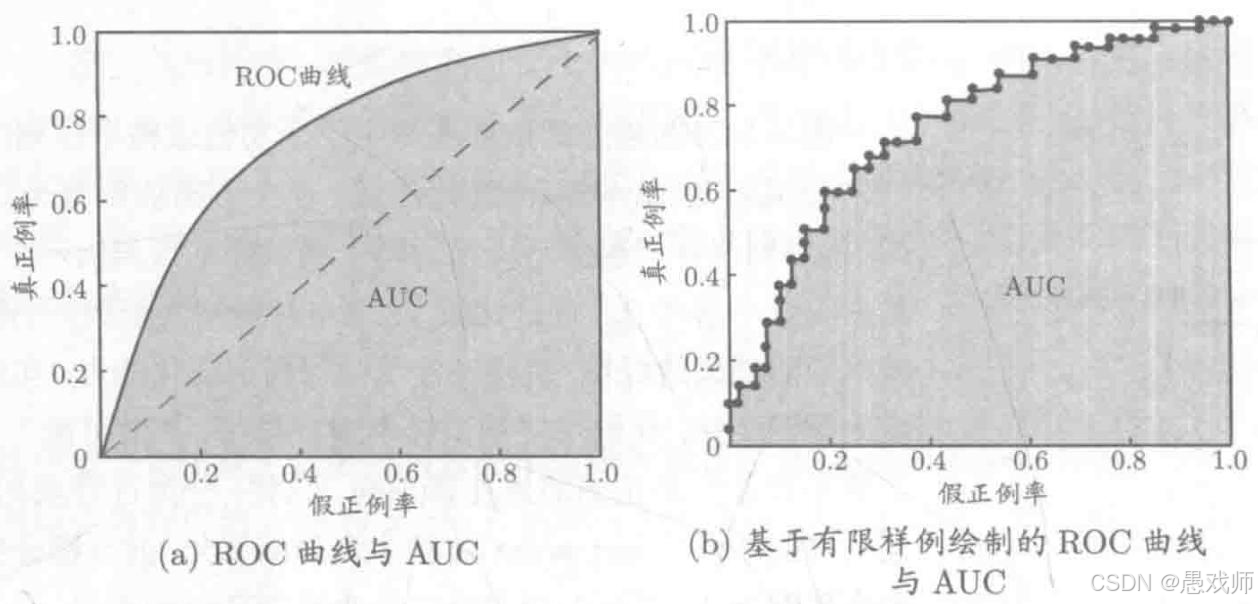
?引用自西瓜書?

ROC曲線核心：

橫軸 (FPR - False Positive Rate):?FPR = FP / (FP + TN) = FP / N。代價：?誤把負例判為正例的比例。我們希望它越低越好。
縱軸 (TPR - True Positive Rate / Recall / Sensitivity):?TPR = TP / (TP + FN) = TP / P。收益：?正確識別出正例的比例。我們希望它越高越好。
本質：?ROC曲線描繪了當分類器的判別閾值(threshold)?從最嚴格（所有樣本判負，TPR=0， FPR=0）到最寬松（所有樣本判正，TPR=1， FPR=1）連續變化時，模型在“收益(TPR)”和“代價(FPR)”之間做出的權衡(Trade-off)，即為了獲得更高的正類識別率 (TPR)，愿意承受多少負類的誤報率 (FPR)。
理想點 (0,1):?FPR=0（沒有誤判負例），TPR=1（所有正例都被正確識別）。完美分類器。

AUC核心：

定義：?ROC曲線下的面積，取值范圍[0, 1]。
物理意義 (最重要！)：?隨機選取一個正樣本和一個負樣本，分類器給正樣本的打分高于給負樣本打分的概率。即?AUC = P(Score? > Score?)。

????????解讀：

AUC = 0.5：模型沒有區分能力（等價于隨機猜測）。
AUC > 0.5：模型具有一定的區分能力。值越接近1，區分能力越強。
AUC < 0.5：模型性能比隨機猜測還差（通常意味著模型預測反了，將正負類標簽互換即可得到?AUC > 0.5?的模型）。
優點：?AUC值是一個單一標量，綜合評估了模型在不同閾值下的整體性能，非常適合用于模型排序（哪個模型更好）。

計算 AUC (Area Under the ROC Curve) 主要有兩種常用方法，它們本質上是等價的，但在實現上各有側重

?方法一：基于物理意義/排序法 (更常用、更高效)

這種方法直接利用 AUC 的物理意義：隨機取一個正樣本和一個負樣本，分類器給正樣本的打分高于負樣本打分的概率。其計算步驟如下：

排序樣本：
- 將所有樣本（包括正樣本和負樣本）按照模型輸出的預測得分/概率進行從高到低排序（最可能為正的排在最前面）。
- 如果多個樣本的預測得分相同，需要特殊處理（見第2步）。
計算秩 (Rank)：
- 給排序后的每個樣本分配一個秩 (Rank)。
- 規則：
  - 得分最高的樣本秩為?n?(總樣本數?n = P + N)。
  - 得分最低的樣本秩為?1。
  - 關鍵：對于預測得分相同的樣本，它們的秩取這些樣本位置序號的?平均值。
    - 例如，排序后第 3, 4, 5 位的樣本得分相同，那么它們的秩都是?(3 + 4 + 5) / 3 = 4。
計算正樣本的秩和：
- 將所有正樣本 (P個)?的秩加起來，得到?SumRank?。
應用公式計算 AUC：
- 使用以下公式：
  AUC = (SumRank? - P*(P+1)/2) / (P * N)

公式推導理解：

核心目標：計算正樣本得分 > 負樣本得分的概率
AUC 的物理意義是：隨機取一個正樣本和一個負樣本，正樣本預測得分高于負樣本的概率。
等價于計算：
滿足?正樣本得分 > 負樣本得分?的 (正, 負) 樣本對數量 ÷ 所有可能的 (正, 負) 樣本對總數
其中：
所有可能的 (正, 負) 樣本對總數 =?P * N
關鍵思路：利用排序后的秩(Rank)
對所有樣本按得分從高到低排序（得分最高排最前面）
給每個樣本分配一個秩(Rank)：
排名第1的樣本 → Rank =?n?(總樣本數?n = P + N)
排名第2的樣本 → Rank =?n-1
...
排名最后的樣本 → Rank =?1
注：得分相同時，取平均秩（后面解釋）
計算所有正樣本的秩之和?→?SumRank?
為什么秩(Rank)能幫我們計算比較結果？
一個樣本的?Rank?值本質表示：有多少個樣本排在它后面（得分比它低）。
因為：
最高分樣本：后面有?n-1?個樣本 → Rank =?n
最低分樣本：后面有?0?個樣本 → Rank =?1
對于任意一個正樣本，它的?Rank?值可拆解為：
Rank? = 排在其后的負樣本數 + 排在其后的正樣本數 + 1
(+1 是因為秩從1開始計數)
推導第1步：展開所有正樣本的秩和
把所有正樣本的 Rank 加起來：
SumRank? = Σ(每個正樣本的Rank) = Σ[ (排在其后的負樣本數) + (排在其后的正樣本數) + 1 ]
拆解成三部分：
=?Σ(排在其后的負樣本數)?+?Σ(排在其后的正樣本數)?+?Σ(1)
其中：
Σ(1)?= 正樣本總數 =?P
Σ(排在其后的正樣本數)?=?正樣本之間的比較次數
（即每個正樣本后面還有幾個其他正樣本）
推導第2步：理解?Σ(排在其后的正樣本數)
想象所有正樣本的排序：
最靠前的正樣本：后面有?(P-1)?個正樣本
第二靠前的正樣本：后面有?(P-2)?個正樣本
...
倒數第二的正樣本：后面有?1?個正樣本
最后的正樣本：后面有?0?個正樣本
所以：
Σ(排在其后的正樣本數) = 0 + 1 + 2 + ... + (P-1) = P(P-1)/2
(等差數列求和公式)
推導第3步：代回秩和公式
將上面結果代回：
SumRank? = Σ(排在其后的負樣本數) + P(P-1)/2 + P
化簡：
=?Σ(排在其后的負樣本數) + P(P+1)/2
因此移項得：
Σ(排在其后的負樣本數) = SumRank? - P(P+1)/2
核心洞見：Σ(排在其后的負樣本數)?就是我們要的答案！
Σ(排在其后的負樣本數)?的實際意義：
遍歷每個正樣本，計算?有多少個負樣本排在該正樣本后面（即得分比該正樣本低）。
這正是?所有滿足?正樣本得分 > 負樣本得分?的 (正, 負) 對的數量！
最終得到AUC公式
滿足條件的正負對數 =?SumRank? - P(P+1)/2
總正負對數 =?P * N
所以：
AUC = [SumRank? - P(P+1)/2] / (P * N)
得分相同的情況如何處理？
當多個樣本得分相同時：
它們在排序中占據連續位置（比如位置 k, k+1, ..., k+m-1）
它們的秩取平均值：(k + (k+1) + ... + (k+m-1)) / m
為什么取平均秩？
物理意義：如果1個正樣本和1個負樣本得分相同，我們認為正樣本 > 負樣本的概率是 0.5（即平局折半）
平均秩的分配方式恰好保證了：
正樣本Rank - 負樣本Rank = 0.5
從而在公式中實現?+0.5?的計數效果

最終計算概率：?(滿足條件的正負對數) / (總正負對數) = [SumRank? - P*(P+1)/2] / (P * N)

例子：
假設有 10 個樣本：3 個正樣本 (P=3)，7 個負樣本 (N=7)。模型預測得分排序后樣本類型和計算的秩如下：

樣本位置 (得分高->低)	1	2	3	4	5	6	7	8	9	10
樣本類型	P	N	P	N	N	N	P	N	N	N
秩 (Rank)	10	9	8	7	6	5	4	3	2	1

正樣本的秩：位置1: 10, 位置3: 8, 位置7: 4
SumRank? = 10 + 8 + 4 = 22
P*(P+1)/2 = 3*4/2 = 6
P*N = 3*7 = 21
AUC = (22 - 6) / 21 = 16 / 21 ≈ 0.7619

方法二：梯形積分法 (基于 ROC 曲線繪制)

這種方法在繪制出 ROC 曲線后，通過計算曲線下的面積來得到 AUC。步驟如下：

繪制 ROC 曲線：
- 按預測得分從高到低排序樣本。
- 設定初始閾值最大：(FPR, TPR) = (0, 0)。
- 依次降低閾值（或依次將每個樣本劃為正例）：
  - 如果當前樣本是?真正例 (TP)：TPR?增加?1/P，點在圖上?垂直向上?移動?1/P。
  - 如果當前樣本是?假正例 (FP)：FPR?增加?1/N，點在圖上?水平向右?移動?1/N。
  - 關鍵：遇到預測得分相同的樣本時，將它們一起處理：
    - 計算這批得分相同的樣本中真正的正例數 (TP_batch) 和假正例數 (FP_batch)。
    - TPR?一次性增加?TP_batch / P。
    - FPR?一次性增加?FP_batch / N。
    - 在圖上從上一個點?(FPR_prev, TPR_prev)?移動到新點?(FPR_prev + FP_batch/N, TPR_prev + TP_batch/P)。
- 最終到達?(1, 1)。
計算曲線下面積：
- 將 ROC 曲線看作由一系列連續的點?(x_i, y_i)?連接而成（包括起點?(0, 0)?和終點?(1, 1)）。
- 使用?梯形法則 (Trapezoidal Rule)?計算曲線下的面積：
  AUC = Σ? [ (x??? - x?) * (y? + y???) / 2 ]
- 這個公式計算的是相鄰兩點?(x?, y?)?和?(x???, y???)?之間形成的梯形面積，然后將所有梯形面積求和。
- 也可以寫成：
  AUC = (1/2) * Σ? [ (x??? - x?) * (y? + y???) ]

例子：?(使用上例數據)
假設繪制 ROC 曲線得到以下關鍵點（按順序）：
(x, y) = (0, 0), (0, 1/3), (1/7, 1/3), (1/7, 2/3), (2/7, 2/3), (2/7, 1), (1, 1)

計算相鄰點間梯形面積：
- (0,0) -> (0, 1/3):?(0-0)*(0 + 1/3)/2 + (1/3 - 0)*(0 + 0)/2??特殊處理：垂直移動，寬度為0，面積為0。
- (0, 1/3) -> (1/7, 1/3): 水平移動?Δx = 1/7,?y? = y? = 1/3。面積 =?(1/7) * (1/3 + 1/3)/2 = (1/7) * (2/3)/2 = (1/7)*(1/3) = 1/21
- (1/7, 1/3) -> (1/7, 2/3): 垂直移動?Δx=0, 面積為0。
- (1/7, 2/3) -> (2/7, 2/3): 水平移動?Δx=1/7,?y?=y?=2/3。面積 =?(1/7) * (2/3 + 2/3)/2 = (1/7) * (4/3)/2 = (1/7)*(2/3) = 2/21
- (2/7, 2/3) -> (2/7, 1): 垂直移動?Δx=0, 面積為0。
- (2/7, 1) -> (1, 1): 水平移動?Δx=5/7,?y?=y?=1。面積 =?(5/7) * (1 + 1)/2 = (5/7)*1 = 5/7
總 AUC = 0 + 1/21 + 0 + 2/21 + 0 + 5/7 = (1/21 + 2/21) + 15/21 = 3/21 + 15/21 = 18/21 = 6/7 ≈ 0.8571`
- 注意：這個例子中的點序列和計算只是為了演示梯形法，結果與排序法例子的結果不同，因為樣本類型和順序是假設的。