基于 LSTM 與 SVM 融合的時間序列預測模型：理論框架與協同機制

1、單一模型的局限性：混合架構的設計動機

2、LSTM 的時序特征提取：從原始序列到高階表征

2.1、門控機制的時序過濾能力

2.2、隱藏狀態的特征壓縮作用

2.3、預訓練的特征優化邏輯

3、SVM 的非線性映射：從高階特征到預測輸出

3.1、核函數對非線性關系的建模能力

3.2、小樣本場景下的泛化優勢

3.3、對冗余特征的 “免疫性”

4、混合模型的協同機制：1+1>2 的核心邏輯

4.1、特征傳遞的層級性

4.2、誤差矯正的互補性

4.3、計算效率的平衡性

5、應用場景與理論延伸

6、完整代碼

7、實驗結果

8、補充：評估模式和訓練模式的區別？

8.1、評估模式與訓練模式的核心區別

8.2、特征提取時必須用評估模式的 3 個關鍵原因

8.2.1、避免特征隨機性波動

8.2.2、保證特征分布與訓練一致

8.2.3、確保特征完整度

時間序列預測是金融、氣象、交通等領域的核心問題，其本質是通過挖掘數據中的時序規律，對未來狀態進行推斷。傳統單一模型（如純 LSTM 或純 SVM）在處理復雜時序數據時往往存在局限性：LSTM 雖擅長捕捉長短期依賴，卻可能因過度擬合時序噪聲導致泛化能力不足；SVM 雖在非線性映射上表現優異，卻難以直接處理原始時序序列的動態特征。本文基于 “LSTM+SVM” 混合模型的實現邏輯，從理論層面闡述其設計原理、協同機制及應用價值，揭示混合模型如何突破單一模型的瓶頸。

1、單一模型的局限性：混合架構的設計動機

時間序列數據的核心挑戰在于時序依賴性與非線性特征的雙重復雜性。單一模型在應對這一挑戰時存在明顯短板：

模型類型	核心優勢	局限性
LSTM（深度學習）	1. 通過門控機制捕捉長短期時序依賴 2. 自動學習時序特征的動態演化規律	1. 對噪聲敏感，易過度擬合時序波動 2. 高維輸出特征的非線性映射能力有限 3. 訓練需大量數據，小樣本場景泛化性差
SVM（傳統機器學習）	1. 通過核函數實現低維到高維的非線性映射 2. 基于結構風險最小化，小樣本泛化能力強 3. 對高維特征的冗余信息不敏感	1. 無法直接處理原始時序序列的動態依賴 2. 依賴人工特征工程，難以捕捉時序深層規律

混合模型的設計邏輯正是 “取長補短”：利用 LSTM 的時序特征提取能力處理動態依賴，再通過 SVM 的非線性擬合能力優化預測精度，形成 “特征提取 — 非線性映射” 的二級處理流程。

2、LSTM 的時序特征提取：從原始序列到高階表征

LSTM（長短期記憶網絡）作為循環神經網絡（RNN）的變種，其核心價值在于通過門控機制解決傳統 RNN 的 “梯度消失” 問題，實現對長序列依賴的有效捕捉。在混合模型中，LSTM 的角色是 “時序特征提取器”，其工作原理可分解為三個層次：

2.1、門控機制的時序過濾能力

LSTM 通過遺忘門、輸入門和輸出門的協同作用，動態篩選時序信息：

遺忘門：過濾無關歷史噪聲（如股票價格的短期隨機波動）；
輸入門：保留關鍵新信息（如突發政策對價格的影響）；
輸出門：生成當前時間步的有效特征表示。
這種機制使 LSTM 能從原始序列（如代碼中的收盤價、成交量、波動率）中提煉出蘊含時序規律的高階特征（如趨勢延續性、波動聚集性）。

2.2、隱藏狀態的特征壓縮作用

在代碼實現中，LSTM 的最終輸出是 “最后一層隱藏狀態”（hn[-1]），其維度由hidden_size（如 64）控制。這一過程本質是特征壓縮：將長度為 20 的原始序列（sequence_length=20）和 5 維特征（收盤價、MA10 等）壓縮為 64 維的緊湊向量，既保留核心時序模式，又降低后續模型的計算復雜度。

2.3、預訓練的特征優化邏輯

代碼中 LSTM 通過全連接層（nn.Linear(hidden_size, 1)）與 MSE 損失函數進行預訓練，其目的并非直接預測，而是引導 LSTM 學習 “對預測有價值的特征”。這種 “有監督的特征學習” 確保提取的隱藏狀態與目標變量（如收盤價）存在強相關性，為后續 SVM 的預測奠定基礎。

3、SVM 的非線性映射：從高階特征到預測輸出

SVM（支持向量機）通過核函數實現低維特征到高維空間的非線性映射，在混合模型中承擔 “最終預測器” 的角色。其與 LSTM 的協同邏輯體現在三個方面：

3.1、核函數對非線性關系的建模能力

代碼中采用 RBF（徑向基函數）核，其本質是通過非線性變換將 LSTM 輸出的 64 維特征映射到更高維空間，使原本線性不可分的特征關系變得可分。例如，股票價格的 “趨勢反轉” 往往依賴于 “波動率放大 + 成交量驟增” 的聯合條件，SVM 能通過核函數捕捉這種復雜交互特征，而 LSTM 單獨預測時易忽略此類非線性組合。

3.2、小樣本場景下的泛化優勢

SVM 基于 “結構風險最小化” 原則，通過最大化分類間隔（回歸場景中為最小化 ε- 不敏感損失）降低過擬合風險。在金融時間序列等小樣本場景中（如代碼中僅 500 條數據），SVM 能有效利用 LSTM 提取的緊湊特征，避免深度學習模型對數據量的過度依賴。

3.3、對冗余特征的 “免疫性”

LSTM 輸出的高階特征可能包含少量冗余信息（如重復的趨勢特征），而 SVM 通過支持向量的選擇機制，僅關注對預測起關鍵作用的特征組合，進一步提升模型的穩健性。

4、混合模型的協同機制：1+1>2 的核心邏輯

LSTM 與 SVM 的融合并非簡單拼接，而是通過 “時序特征提取 — 非線性映射” 的流水線式協同，實現對時間序列復雜性的分層破解。其核心機制可概括為三個層面：

4.1、特征傳遞的層級性

原始數據（如收盤價、成交量）首先經 LSTM 處理，轉化為蘊含時序規律的高階特征（隱藏狀態），再傳遞給 SVM 進行最終預測。這種 “原始數據→時序特征→預測結果” 的層級傳遞，使模型能分階段處理數據的不同屬性：LSTM 專注于 “時序動態性”，SVM 專注于 “特征非線性”，避免單一模型同時應對雙重復雜性。

4.2、誤差矯正的互補性

LSTM 的預測誤差往往源于對短期噪聲的過度擬合，而 SVM 的誤差多源于對長周期趨勢的捕捉不足。混合模型中，LSTM 的高階特征過濾了部分噪聲，SVM 的核函數又強化了對趨勢的非線性建模，兩者誤差形成互補，最終降低整體預測偏差（如代碼中通過 MSE 和 R2 評估的優化效果）。

4.3、計算效率的平衡性

LSTM 的訓練復雜度隨序列長度呈線性增長，而 SVM 的復雜度隨樣本量呈平方增長。混合模型中，LSTM 的特征壓縮（如 64 維隱藏狀態）大幅降低了 SVM 的輸入維度，在保證精度的同時平衡了計算成本，使模型更適用于實時預測場景（如高頻交易中的價格預測）。

5、應用場景與理論延伸

LSTM+SVM 混合模型的理論框架不僅適用于金融時間序列，還可推廣至其他時序預測領域：

氣象預測：LSTM 提取氣溫、濕度的時序依賴，SVM 捕捉 “溫度 - 降水” 的非線性關系；
交通流量預測：LSTM 學習早晚高峰的周期性規律，SVM 建模特殊事件（如節假日）的突發波動；
工業故障預測：LSTM 挖掘設備傳感器數據的趨勢變化，SVM 識別 “振動 - 溫度” 的異常關聯。

6、完整代碼

"""
文件名: LSTM+SVM
作者: 墨塵
日期: 2025/7/27
項目名: d2l_learning
備注: 基于LSTM和SVM的混合模型進行時間序列預測，結合了深度學習和傳統機器學習的優勢
"""
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import torch
import torch.nn as nn
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, r2_score# 設置中文字體，確保圖表中的中文正常顯示
plt.rcParams["font.family"] = ["SimHei"]  # 指定默認中文字體
plt.rcParams["axes.unicode_minus"] = False  # 解決負號顯示問題class LSTMFeatureExtractor(nn.Module):"""LSTM特征提取器：將時序數據轉換為固定維度的特征向量，用于后續的SVM回歸"""def __init__(self, input_size, hidden_size, num_layers=1, dropout=0.0):"""初始化LSTM特征提取器參數:input_size: 輸入特征的維度hidden_size: LSTM隱藏層的維度num_layers: LSTM層數dropout: Dropout概率，用于防止過擬合"""super().__init__()# 定義LSTM層，batch_first=True表示輸入格式為(batch, seq_len, feature)self.lstm = nn.LSTM(input_size=input_size,hidden_size=hidden_size,num_layers=num_layers,batch_first=True,dropout=dropout,bidirectional=False  # 使用單向LSTM)# 添加全連接層，將LSTM的隱藏狀態映射到與目標變量相同的維度# 這用于訓練LSTM學習有意義的特征表示self.fc = nn.Linear(hidden_size, 1)def forward(self, x):"""前向傳播函數，定義數據如何通過網絡參數:x: 輸入張量，形狀為(batch_size, sequence_length, input_size)返回:output: 預測值，形狀為(batch_size, 1)"""# LSTM的輸出格式為(output, (h_n, c_n))# output: 每個時間步的隱藏狀態，形狀為(batch_size, seq_len, hidden_size)# h_n: 最后一個時間步的隱藏狀態，形狀為(num_layers, batch_size, hidden_size)# c_n: 最后一個時間步的細胞狀態，形狀同上_, (hn, _) = self.lstm(x)# 提取最后一層的隱藏狀態，形狀調整為(batch_size, hidden_size)last_hidden = hn[-1]# 通過全連接層得到最終輸出，形狀為(batch_size, 1)output = self.fc(last_hidden)return outputdef create_sequences(df, target_col="Close", seq_len=20):"""將時間序列數據轉換為監督學習格式（序列-目標對）參數:df: 包含特征的DataFrametarget_col: 目標變量列名seq_len: 序列長度（用于預測的歷史時間步數）返回:X: 特征序列，形狀為(samples, seq_len, features)y: 目標值，形狀為(samples,)"""X, y = [], []for i in range(seq_len, len(df)):X.append(df.iloc[i - seq_len:i].values)  # 歷史特征序列y.append(df.iloc[i][target_col])         # 對應的目標值return np.array(X), np.array(y)def plot_training_loss(losses, epochs):"""可視化訓練過程中的損失變化"""plt.figure(figsize=(10, 5))plt.plot(range(epochs), losses, 'b-', linewidth=2)plt.title('訓練損失變化')plt.xlabel('Epoch')plt.ylabel('損失值 (MSE)')plt.grid(True, linestyle='--', alpha=0.7)plt.tight_layout()plt.savefig('training_loss.png')  # 保存圖表plt.close()def plot_prediction_vs_actual(dates, actual, predicted, title="預測值與真實值對比"):"""可視化預測結果與真實值對比"""plt.figure(figsize=(14, 6))plt.plot(dates, actual, 'g-', label='真實值', linewidth=2)plt.plot(dates, predicted, 'r--', label='預測值', linewidth=2)plt.title(title)plt.xlabel('日期')plt.ylabel('價格 (標準化后)')plt.legend()plt.grid(True, linestyle='--', alpha=0.7)plt.tight_layout()plt.savefig('prediction_results.png')  # 保存圖表plt.close()def main():"""主函數：協調數據處理、模型訓練和評估的整個流程"""# 步驟1: 生成虛擬金融數據print("正在生成虛擬金融數據...")date_range = pd.date_range(start="2023-01-01", periods=500, freq="D")price = np.cumsum(np.random.randn(500)) + 100  # 隨機游走模擬股票價格volume = np.random.randint(100, 1000, size=500)  # 隨機成交量data = pd.DataFrame({"Date": date_range,"Close": price,"Volume": volume}).set_index("Date")  # 設置日期為索引# 步驟2: 添加技術指標print("正在計算技術指標...")data["MA10"] = data["Close"].rolling(window=10).mean()  # 10日移動平均線data["Return"] = data["Close"].pct_change()  # 每日收益率data["Volatility"] = data["Return"].rolling(window=10).std()  # 10日滾動波動率data.dropna(inplace=True)  # 刪除包含NaN的行，確保數據完整性# 步驟3: 數據可視化print("正在生成數據可視化圖表...")# 可視化1: 收盤價與MA10plt.figure(figsize=(12, 5))plt.plot(data.index, data["Close"], label="收盤價", color="red")plt.plot(data.index, data["MA10"], label="10日移動平均線", color="green")plt.title("收盤價 vs. 10日移動平均線")plt.legend()plt.tight_layout()plt.savefig("price_vs_ma10.png")plt.close()# 可視化2: 成交量plt.figure(figsize=(12, 3))plt.bar(data.index, data["Volume"], color="blue")plt.title("成交量隨時間變化")plt.tight_layout()plt.savefig("volume.png")plt.close()# 可視化3: 收益率分布plt.figure(figsize=(8, 4))sns.histplot(data["Return"], bins=50, kde=True, color="purple")plt.title("收益率分布")plt.tight_layout()plt.savefig("return_distribution.png")plt.close()# 可視化4: 波動率plt.figure(figsize=(12, 3))plt.plot(data.index, data["Volatility"], color="green")plt.title("波動率隨時間變化 (10日滾動標準差)")plt.tight_layout()plt.savefig("volatility.png")plt.close()# 步驟4: 數據預處理print("正在進行數據預處理...")features = ["Close", "MA10", "Return", "Volatility", "Volume"]  # 選擇用于預測的特征sequence_length = 20  # 使用前20天的數據預測下一天# 數據標準化：將所有特征縮放到均值為0，標準差為1的分布scaler = StandardScaler()scaled_data = scaler.fit_transform(data[features])scaled_df = pd.DataFrame(scaled_data, index=data.index, columns=features)# 構造序列數據：將時間序列轉換為監督學習格式X, y = create_sequences(scaled_df, "Close", sequence_length)# 劃分訓練集和測試集（按時間順序劃分，保持數據的時序性）test_size = 0.2split_idx = int(len(X) * (1 - test_size))X_train, X_test = X[:split_idx], X[split_idx:]y_train, y_test = y[:split_idx], y[split_idx:]test_dates = data.index[-len(y_test):]  # 記錄測試集對應的日期print(f"訓練集大小: {len(X_train)}, 測試集大小: {len(X_test)}")# 步驟5: 轉換為PyTorch張量X_train_tensor = torch.tensor(X_train, dtype=torch.float32)X_test_tensor = torch.tensor(X_test, dtype=torch.float32)# 增加一個維度，使其形狀為(batch_size, 1)，與模型輸出匹配y_train_tensor = torch.tensor(y_train, dtype=torch.float32).unsqueeze(1)# 步驟6: 定義并訓練LSTM特征提取器print("正在訓練LSTM特征提取器...")input_size = len(features)  # 輸入特征維度hidden_size = 64  # LSTM隱藏層維度lstm = LSTMFeatureExtractor(input_size, hidden_size)optimizer = torch.optim.Adam(lstm.parameters(), lr=0.001)  # Adam優化器loss_fn = nn.MSELoss()  # 均方誤差損失函數，用于回歸問題n_epochs = 30  # 訓練輪數training_losses = []  # 記錄每輪的訓練損失for epoch in range(n_epochs):lstm.train()  # 設置為訓練模式optimizer.zero_grad()  # 梯度清零output = lstm(X_train_tensor)  # 前向傳播loss = loss_fn(output, y_train_tensor)  # 計算損失loss.backward()  # 反向傳播optimizer.step()  # 更新參數training_losses.append(loss.item())if epoch % 5 == 0:print(f"[Epoch {epoch+1}/{n_epochs}] Loss: {loss.item():.4f}")# 可視化訓練損失變化plot_training_loss(training_losses, n_epochs)# 步驟7: 提取LSTM特征print("正在提取LSTM特征...")lstm.eval()  # 設置為評估模式with torch.no_grad():  # 不計算梯度，節省內存和計算資源# 提取LSTM最后一層的隱藏狀態作為特征# 這些特征將被用于訓練SVM模型_, (train_feats, _) = lstm.lstm(X_train_tensor)train_feats = train_feats[-1].numpy()  # 取最后一層的隱藏狀態_, (test_feats, _) = lstm.lstm(X_test_tensor)test_feats = test_feats[-1].numpy()# 步驟8: 訓練SVM回歸模型print("正在訓練SVM回歸模型...")# 使用RBF核函數的SVM回歸器，C是正則化參數，epsilon控制允許的誤差范圍svm = SVR(kernel="rbf", C=100, epsilon=0.01)svm.fit(train_feats, y_train)  # 訓練SVM模型# 步驟9: 模型評估print("正在評估模型性能...")predictions = svm.predict(test_feats)  # 預測測試集# 計算評估指標mse = mean_squared_error(y_test, predictions)  # 均方誤差r2 = r2_score(y_test, predictions)  # 決定系數，解釋方差的比例print(f"\nSVM模型評估結果:")print(f"MSE: {mse:.4f}, R2: {r2:.4f}")# 步驟10: 可視化預測結果plot_prediction_vs_actual(test_dates, y_test, predictions, "標準化價格預測值與真實值對比")print("模型訓練和評估完成！")print("圖表已保存至當前目錄下的PNG文件中")if __name__ == "__main__":main()  # 程序入口點

7、實驗結果

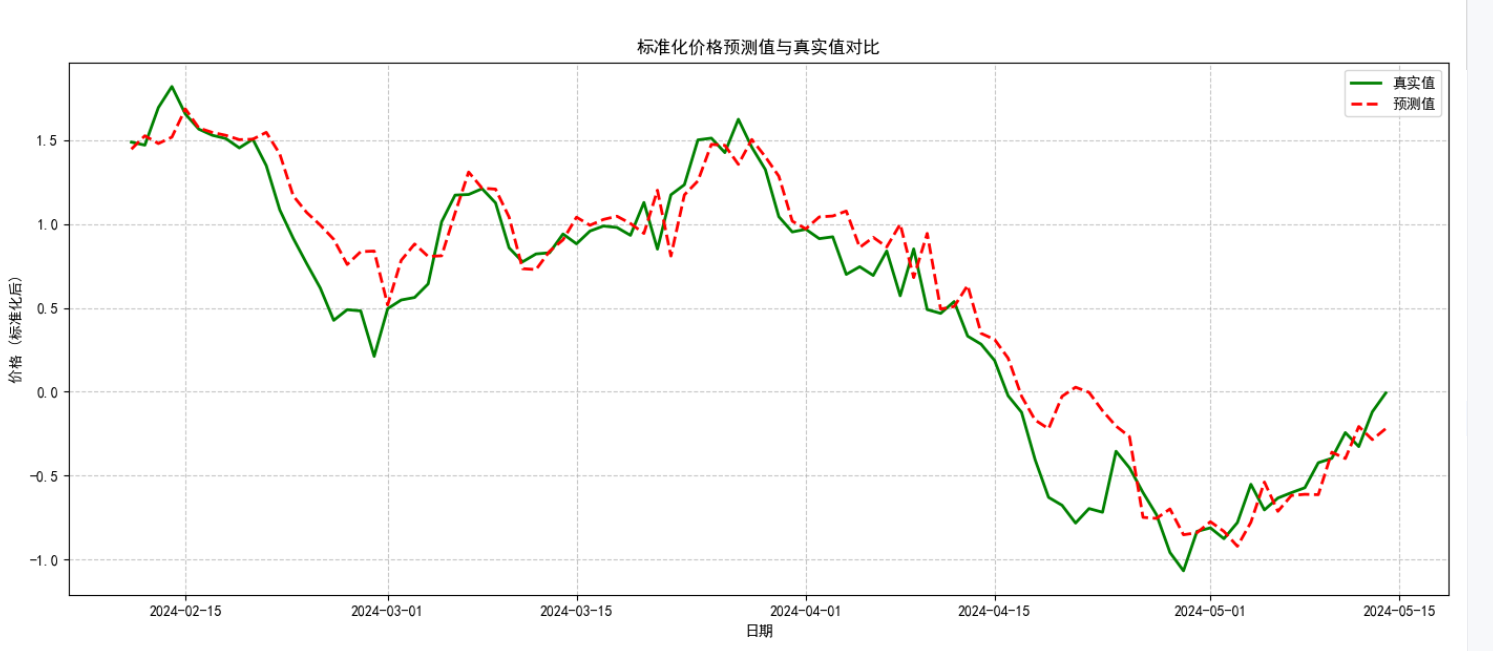
8、補充：評估模式和訓練模式的區別？

8.1、評估模式與訓練模式的核心區別

模型在訓練和評估時的行為存在本質差異，主要體現在隨機性操作的啟用與否：

模式	核心特點	典型隨機性操作
訓練模式（train mode）	啟用隨機性操作，用于模型參數學習	1. Dropout 層隨機丟棄部分神經元 2. Batch Normalization 使用當前批次的均值和方差 3. 隨機數據增強（如隨機裁剪、翻轉）
評估模式（eval mode）	關閉隨機性操作，用于穩定推理	1. Dropout 層不丟棄神經元（保留全部特征） 2. Batch Normalization 使用訓練時保存的全局均值和方差 3. 關閉數據增強（使用原始數據）