深度學習（魚書）day04–手寫數字識別項目實戰

魚書的相關源代碼下載：
點擊鏈接：http://www.ituring.com.cn/book/1921
點擊“隨書下載”

第三項就是源代碼：

解壓后，在pycharm（或其它IDE）中打開此文件夾查看或運行即可。（紅框內是本人自建的文件）

一、MNIST數據集

• 和求解機器學習問題的步驟（分成學習和推理兩個階段進行）一樣，使用神經網絡解決問題時，也需要首先使用訓練數據（學習數據）進行權重參數的學習；進行推理時，使用剛才學習到的參數，對輸入數據進行分類。

• 這里我們來進行手寫數字圖像的分類。假設學習已經全部結束，我們使用學習到的參數，先實現神經網絡的“推理處理”。這個推理處理也稱為神經網絡的前向傳播（forward propagation）。

• 這里使用的數據集是MNIST手寫數字圖像集。MNIST是機器學習領域最有名的數據集之一，被應用于從簡單的實驗到發表的論文研究等各種場合。MNIST數據集是由0到9的數字圖像構成的。訓練圖像有6萬張，測試圖像有1萬張，這些圖像可以用于學習和推理。MNIST數據集的一般使用方法是，先用訓練圖像進行學習，再用學習到的模型度量能在多大程度上對測試圖像進行正確的分類。
  

• MNIST的圖像數據是28像素 × 28像素的灰度圖像（1通道），各個像素的取值在0到255之間。每個圖像數據都相應地標有“7”“2”“1”等標簽。

本書提供了便利的Python腳本mnist.py，該腳本支持從下載MNIST數據集到將這些數據轉換成NumPy數組等處理（mnist.py在dataset目錄下）。使用mnist.py時，當前目錄必須是ch01、ch02、ch03、…、ch08目錄中的一個。使用mnist.py中的load_mnist()函數，就可以按下述方式輕松讀入MNIST數據。

import sys, os
sys.path.append(os.pardir)  # 為了導入父目錄中的文件而進行的設定
from dataset.mnist import load_mnist(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)print(x_train.shape)
print(t_train.shape)
print(x_test.shape)
print(t_test.shape)

load_mnist()它負責加載并預處理 MNIST 數據集，使其適合機器學習模型的訓練和測試。

def load_mnist(normalize=True, flatten=True, one_hot_label=False):"""讀入MNIST數據集Parameters----------normalize : 將圖像的像素值正規化為0.0~1.0one_hot_label : one_hot_label為True的情況下，標簽作為one-hot數組返回one-hot數組是指[0,0,1,0,0,0,0,0,0,0]這樣的數組flatten : 是否將圖像展開為一維數組Returns-------(訓練圖像, 訓練標簽), (測試圖像, 測試標簽)"""if not os.path.exists(save_file):init_mnist()with open(save_file, 'rb') as f:dataset = pickle.load(f)if normalize:for key in ('train_img', 'test_img'):dataset[key] = dataset[key].astype(np.float32)dataset[key] /= 255.0if one_hot_label:dataset['train_label'] = _change_one_hot_label(dataset['train_label'])dataset['test_label'] = _change_one_hot_label(dataset['test_label'])if not flatten:for key in ('train_img', 'test_img'):dataset[key] = dataset[key].reshape(-1, 1, 28, 28)return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label']) 

下面詳細解釋這個函數的功能、參數和返回值：

參數說明

1. normalize（默認 True）
   • 是否對圖像像素值進行歸一化（將 0-255的像素值縮放到 0.0-1.0的浮點數）。
   • 如果設為 False，則保持原始的 0-255的 uint8格式。
2. flatten（默認 True）
   • 是否將圖像展平為一維數組（784維向量）。
   • 如果設為 False，則保留原始圖像形狀 (1, 28, 28)（單通道，28×28 像素）。
3. one_hot_label（默認 False）
   • 是否將標簽轉換為 one-hot 編碼（例如，數字 3變為 [0, 0, 0, 1, 0, 0, 0, 0, 0, 0]）。
   • 如果設為 False，則標簽保持為原始的數字（0-9）。

Python有 pickle這個便利的功能。這個功能可以將程序運行中的對象保存為文件。如果加載保存過的 pickle文件，可以立刻復原之前程序運行中的對象。用于讀入MNIST數據集的load_mnist()函數內部也使用了 pickle功能（在第 2次及以后讀入時）。利用 pickle功能，可以高效地完成MNIST數據的準備工作。

顯示MNIST圖像：

import sys, os
sys.path.append(os.pardir)  # 為了導入父目錄中的文件而進行的設定
from dataset.mnist import load_mnist
import numpy as np
from PIL import Imagedef img_show(img):pil_img = Image.fromarray(np.uint8(img))pil_img.show()(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)img = x_train[1]
label = t_train[1]
print(label)
print(img.shape)img = img.reshape(28, 28)
print(img.shape)img_show(img)

注意的是，flatten=True時讀入的圖像是以一列（一維）NumPy數組的形式保存的，因此，顯示圖像時，需要把它變為原來的28像素 × 28像素的形狀

二、神經網絡的推理處理

神經網絡的輸入層有784個神經元，輸出層有10個神經元。

輸入層的784這個數字來源于圖像大小的28 × 28 = 784，輸出層的10這個數字來源于10類別分類（數字0到9，共10類別）。

此外，這個神經網絡有2個隱藏層，第1個隱藏層有50個神經元，第2個隱藏層有100個神經元。這個50和100可以設置為任何值。下面我們先定義**get_data()、init_network()、predict()**這3個函數。

def get_data():(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)return x_test, t_testdef init_network():with open("sample_weight.pkl", 'rb') as f:network = pickle.load(f)return networkdef predict(network, x):W1, W2, W3 = network['W1'], network['W2'], network['W3']b1, b2, b3 = network['b1'], network['b2'], network['b3']a1 = np.dot(x, W1) + b1z1 = sigmoid(a1)a2 = np.dot(z1,W2)z2 = sigmoid(a2)a3 = np.dot(z2, W3) + b3y = softmax(a3)return y

init_network()會讀入保存在pickle文件sample_weight.pkl中的學習到的權重參數。這個文件中以字典變量的形式保存了權重和偏置參數。我們用這3個函數來實現神經網絡的推理處理。然后，評價它的識別精度（accuracy），即能在多大程度上正確分類。

因為之前我們假設學習已經完成，所以學習到的參數被保存下來。假設保存在sample_weight.pkl文件中，在推理階段，我們直接加載這些已經學習到的參數。

x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):y = predict(network, x[i])p = np.argmax(y) # 獲取概率最大的下標if p == t[i]:accuracy_cnt += 1
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

predict()函數以NumPy數組的形式輸出各個標簽對應的概率。比如輸出[0.1, 0.3, 0.2, …, 0.04]的數組，該數組表示“0”的概率為0.1，“1”的概率為0*.*3。

我們取出這個概率列表中的最大值的索引（第幾個元素的概率最高），作為預測結果。可以用np.argmax(x)函數取出數組中的最大值的索引，np.argmax(x)將獲取被賦給參數x的數組中的最大值元素的索引。

最后，比較神經網絡所預測的答案和正確解標簽，將回答正確的概率作為識別精度。

正規化：將normalize設置成True后，函數內部會進行轉換，將圖像的各個像素值除以255，使得數據的值在0.0～1.0的范圍內。像這樣把數據限定到某個范圍內的處理稱為正規化（normalization）。

預處理：對神經網絡的輸入數據進行某種既定的轉換稱為預處理（pre-processing）。這里，作為對輸入圖像的一種預處理，我們進行了正規化。

實際上，很多預處理都會考慮到數據的整體分布。比如，利用數據整體的均值或標準差，移動數據，使數據整體以 0為中心分布，或者進行正規化，把數據的延展控制在一定范圍內。除此之外，還有將數據整體的分布形狀均勻化的方法，即數據白化（whitening）等。

三、批處理

network = init_network()
W1, W2, W3 = network['W1'], network['W2'], network['W3']
print(x.shape)
print(x[0].shape)
print(W1.shape)
print(W2.shape)
print(W3.shape)

通過上述結果來確認一下多維數組的對應維度的元素個數是否一致，省略了偏置：

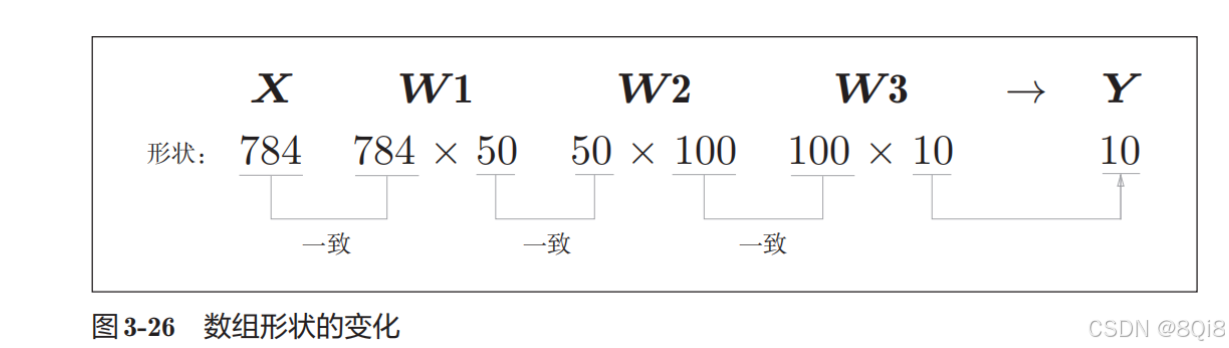
現在我們來考慮打包輸入多張圖像的情形。比如，我們想用predict()函數一次性打包處理100張圖像。為此，可以把x的形狀改為100 × 784，將100張圖像打包作為輸入數據：

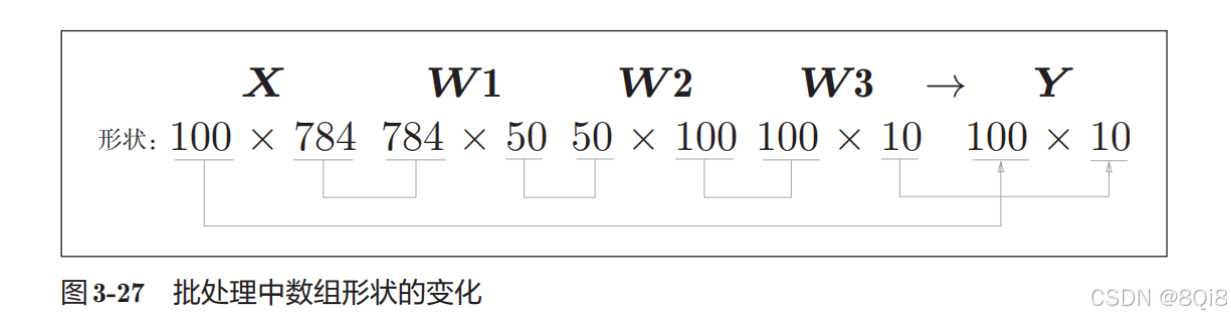
輸出數據的形狀為100 × 10。這表示輸入的100張圖像的結果被一次性輸出了。比如，x[0]和y[0]中保存了第0張圖像及其推理結果，x[1]和y[1]中保存了第1張圖像及其推理結果。

這種打包式的輸入數據稱為批（batch）。批有“捆”的意思，圖像就如同紙幣一樣扎成一捆。

批處理可以縮短處理時間。這是因為大多數處理數計算的庫都進行了能夠高效處理大型數組運算的最優化。并且，在神經網絡的運算中，當數據傳送成為瓶頸時，批處理可以減輕數據總線的負荷（嚴格地講，相對于數據讀入，可以將更多的時間用在計算上）。也就是說，批處理一次性計算大型數組要比分開逐步計算各個小型數組速度更快。

batch_size = 100 # 批數量
accuracy_cnt = 0
for i in range(0,len(x),batch_size):batch_x = x[i:i+batch_size]batch_y = predict(network, x[i:i+batch_size])p = np.argmax(batch_y,axis=1)  # 獲取概率最大的下標accuracy_cnt += np.sum(p == t[i:i+batch_size])
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

部分代碼詳解：

range()函數若指定為range(start, end)，則會生成一個由start到end-1之間的整數構成的列表。range(start, end, step)這樣指定3個整數，則生成的列表中的下一個元素會增加step指定的值。

x[i:i+batch_n]會取出從第i個到第i+batch_n個之間的數據。本例中是像x[0:100]、x[100:200]……這樣，從頭開始以100為單位將數據提取為批數據。

list( range(0, 10) ) # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]list( range(0, 10, 3) ) # [0, 3, 6, 9]

通過argmax()獲取值最大的元素的索引。不過這里需要注意的是，我們給定了參數axis=1。這指定了在100 × 10的數組中，沿著**第1維方向（以第1維為軸）**找到值最大的元素的索引（第0維對應第1個維度）

• 矩陣的第0維是列方向，第1維是行方向。

x = np.array([[0.1, 0.8, 0.1], [0.3, 0.1, 0.6],[0.2, 0.5, 0.3], [0.8, 0.1, 0.1]])
y = np.argmax(x, axis=1)
print(y) # [1 2 1 0]

使用比較運算符（==）生成由True/False構成的布爾型數組，并計算True的個數：

y = np.array([1, 2, 1, 0])
t = np.array([1, 2, 0, 0])
print(y==t) # [True True False True]
np.sum(y==t) # 3

本文參考了該博主的文章