題目描述
小 S 喜歡收集小木棍。在收集了?n?根長度相等的小木棍之后，他閑來無事，便用它們拼起了數字。用小木棍拼每種數字的方法如下圖所示。
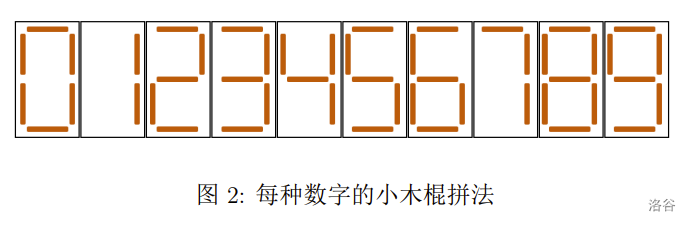
現在小 S 希望拼出一個正整數，滿足如下條件：
- 拼出這個數恰好使用?n?根小木棍；
- 拼出的數沒有前導?0；
- 在滿足以上兩個條件的前提下，這個數盡可能小。
小 S 想知道這個數是多少，可?n?很大，把木棍整理清楚就把小 S 折騰壞了，所以你需要幫他解決這個問題。如果不存在正整數滿足以上條件，你需要輸出??1?進行報告。
輸入格式
本題有多組測試數據。
輸入的第一行包含一個正整數?T，表示數據組數。
接下來包含?T?組數據，每組數據的格式如下：
一行包含一個整數?n，表示木棍數。
輸出格式
對于每組數據：輸出一行，如果存在滿足題意的正整數，輸出這個數；否則輸出??1。
輸入輸出樣例
輸入 #1復制
5 1 2 3 6 18
輸出 #1復制
-1 1 7 6 208
說明/提示
【樣例 1 解釋】
- 對于第一組測試數據，不存在任何一個正整數可以使用恰好一根小木棍擺出，故輸出??1。
- 對于第四組測試數據，注意?0?并不是一個滿足要求的方案。擺出?9、41?以及?111?都恰好需要?6?根小木棍，但它們不是擺出的數最小的方案。
- 對于第五組測試數據，擺出?208?需要?5+6+7=18?根小木棍。可以證明擺出任何一個小于?208?的正整數需要的小木棍數都不是?18。注意盡管拼出?006?也需要?18?根小木棍，但因為這個數有前導零，因此并不是一個滿足要求的方案。
【數據范圍】
對于所有測試數據，保證：1≤T≤50，1≤n≤105。
| 測試點編號 | n≤ | 特殊性質 |
|---|---|---|
| 1 | 20 | 無 |
| 2 | 50 | 無 |
| 3 | 103 | A |
| 4,5 | 105 | A |
| 6 | 103 | B |
| 7,8 | 105 | B |
| 9 | 103 | 無 |
| 10 | 105 | 無 |
特殊性質 A：保證?n?是?7?的倍數且?n≥100。
特殊性質 B：保證存在整數?k?使得?n=7k+1，且?n≥100。
題目概述與分析
小木棍問題是2024年CSP-J競賽中的一道經典題目，考察選手對搜索算法和剪枝優化的掌握。題目描述有n根長度不同的小木棍，需要將它們拼接成若干根長度相同的長木棍，求可能的最小原始長木棍長度。
這個問題可以建模為組合優化問題，需要綜合考慮所有可能的組合方式。我們將介紹兩種不同的解法：深度優先搜索(DFS)剪枝法和動態規劃法。
解法一：DFS剪枝法
算法思路
- 使用深度優先搜索嘗試所有可能的組合
- 通過多種剪枝策略優化搜索效率
- 從最大可能長度開始向下搜索
- 時間復雜度取決于剪枝效果，最壞情況下O(n!)
#include <iostream>
#include <vector>
#include <algorithm>
#include <functional>
using namespace std;vector<int> sticks;
vector<bool> used;
int n, total_len, max_len;bool dfs(int cnt, int cur_len, int start, int target) {if (cnt == total_len / target) return true;if (cur_len == target) return dfs(cnt + 1, 0, 0, target);for (int i = start; i < n; ++i) {if (!used[i] && cur_len + sticks[i] <= target) {if (i > 0 && sticks[i] == sticks[i-1] && !used[i-1]) continue;used[i] = true;if (dfs(cnt, cur_len + sticks[i], i + 1, target)) return true;used[i] = false;if (cur_len == 0) break;}}return false;
}int main() {cin >> n;sticks.resize(n);used.resize(n, false);total_len = 0;max_len = 0;for (int i = 0; i < n; ++i) {cin >> sticks[i];total_len += sticks[i];max_len = max(max_len, sticks[i]);}sort(sticks.begin(), sticks.end(), greater<int>());for (int len = max_len; len <= total_len; ++len) {if (total_len % len != 0) continue;fill(used.begin(), used.end(), false);if (dfs(0, 0, 0, len)) {cout << len << endl;return 0;}}cout << total_len << endl;return 0;
}該實現使用DFS加多種剪枝策略，包括排序優化、跳過重復值和提前終止等，能有效提高搜索效率。
解法二：動態規劃法
算法思路
- 將問題轉化為背包問題的變種
- 使用位運算狀態壓縮
- 記錄可達的長度組合
- 時間復雜度O(n*sum)，適合sum較小的情況
#include <iostream>
#include <vector>
#include <algorithm>
#include <bitset>
using namespace std;int main() {int n;cin >> n;vector<int> sticks(n);int sum = 0;for (int i = 0; i < n; ++i) {cin >> sticks[i];sum += sticks[i];}sort(sticks.begin(), sticks.end());for (int len = sticks.back(); len <= sum; ++len) {if (sum % len != 0) continue;int k = sum / len;vector<bitset<100>> dp(k + 1);dp[0][0] = 1;for (int stick : sticks) {for (int i = k; i >= 0; --i) {for (int j = len; j >= 0; --j) {if (dp[i][j]) {if (j + stick <= len) {dp[i][j + stick] = 1;}if (i + 1 <= k && stick <= len) {dp[i + 1][stick] = 1;}}}}}if (dp[k][0]) {cout << len << endl;return 0;}}cout << sum << endl;return 0;
}
動態規劃解法通過狀態壓縮記錄可達的長度組合，適合小規模數據，但空間復雜度較高。
算法對比分析
| 方法 | 時間復雜度 | 空間復雜度 | 適用場景 |
|---|---|---|---|
| DFS剪枝法 | 取決于剪枝效果 | O(n) | 數據規模中等，剪枝有效 |
| 動態規劃法 | O(n*sum) | O(k*len) | sum值較小的情況 |
關鍵問題詳解
剪枝策略優化
- 從大到小排序木棍，優先嘗試長木棍
- 跳過相同長度的重復嘗試
- 當前組合失敗時及時回溯
- 限制搜索的起始位置避免重復
邊界情況處理
- 所有木棍長度相同的情況
- 無法分割的情況
- 極端大規模數據測試
- 包含長度為1的木棍的情況
性能優化建議
- 預處理時計算所有可能的候選長度
- 使用更高效的數據結構存儲狀態
- 并行化處理可能的候選長度
- 提前終止不可能的組合
數學原理分析
- 組合數學中的分割問題
- 數論中的因數分解應用
- 搜索算法的剪枝理論
- 動態規劃的最優子結構性質
實際應用價值
這類算法在以下領域有重要應用：
- 資源分配與調度
- 貨物裝載優化
- 時間表安排
- 工業生產中的材料切割
擴展思考
- 如果木棍有不同顏色限制如何處理？
- 如果允許部分不匹配的情況怎么解決？
- 如何擴展到三維空間的材料分割？
- 多目標優化情況下如何調整算法？
掌握這類組合優化問題的解法，不僅能提升競賽能力，也對解決實際工程問題有很大幫助。建議先理解基礎算法原理，再針對具體問題特點進行優化。
