樹與二叉樹
樹的定義及相關概念
樹是n(n≥0)個結點的有限集合,n = 0時,稱為空樹,這是一種特殊情況。在任意一棵非空樹中應滿足:
1)有且僅有一個特定的稱為根的結點。
2)當n > 1時,其余結點可分為m(m > 0)個互不相交的有限集合T1, T2,…, Tm,其中每個集合本身又是一棵樹,并且稱為根結點的子樹。
3)樹的根結點沒有前驅結點,其余結點有且僅有一個前驅結點。
4)樹中所有結點可以有零個或多個后繼結點。
樹的基本術語
結點之間的關系描述:則有:祖先結點,子孫結點,雙親結點,孩子節點,兄弟結點,堂兄弟結點,以上完全可以按照樹的結構和親戚對應的關系很方便的區分。如圖所示:
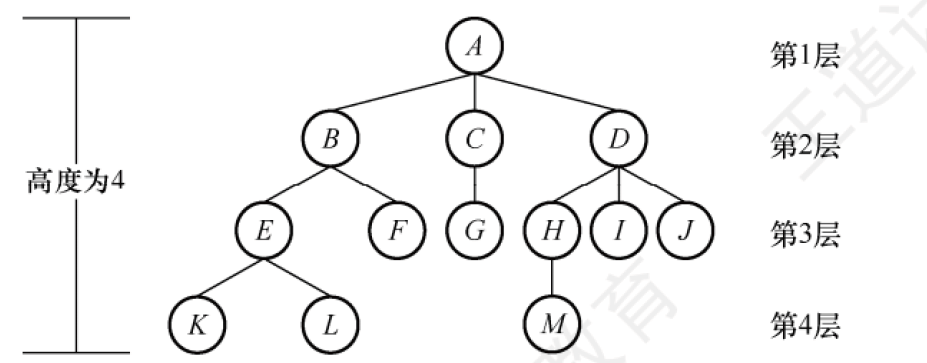
很明顯地可以了解到:B的子孫有EFKL,路徑上的ABE都是K的祖先結點,E是K的雙親(父結點),K是E的子孫結點(孩子),K和L具有相同的雙親E,因此K和L是兄弟結點。結點G和EFHIJ互為堂兄弟結點。(排得差不多了,自己領會吧)。
結點、樹的屬性描述:結點的層次(深度)——從上往下數(從根到該節點的深度,例如B的深度為2),結點的高度——從下往上數,以該結點為根的子樹的高度,例如D的高度為3,樹的高度(深度)——總共多少層,上圖樹高度為4,結點的度——有幾個孩子(分支),B度為2,D度為3,樹的度——各結點的度的最大值。
樹中度大于0的結點為分支結點,度為0的結點為葉子結點。在分支結點中,每個結點的分支數就是該結點的度。
有序樹——邏輯上看,樹中結點的各子樹從左至右是有次序的,不能互換。
無序樹——邏輯上看,樹中結點的各子樹從左至右是無次序的,可以互換。
路徑——路徑是由兩個節點之間所經過的結點序列構成的。
路徑長度——所經過的邊的個數。
森林——森林是m(m≥0)棵互不相交的樹的集合。 ^ac8bfc
樹的性質
證明我就不寫了,留給我自己去推。
- 樹中的結點數等于所有結點的度數加1(加的是根)
- 度為m的樹中第i層至多有mi?1m^{i-1}mi?1個結點
- 高度為h的m叉樹至多有(mh?1)/(m?1)(m^h-1)/(m-1)(mh?1)/(m?1)個結點
- 具有n個結點的m叉樹的最小高度為?logm(n(m?1)+1)?\lceil log_m(n(m-1)+1)\rceil?logm?(n(m?1)+1)?
- 度為m、具有n個結點的樹最大高度為n?m+1n-m+1n?m+1
- 高度為h的m叉樹至少有h個結點。高度為h、度為m的樹至少有h+m-1個結點。
二叉樹的定義及相關概念
二叉樹是n(n≥0)個結點的有限集合:
1)或者為空二叉樹,即n = 0。
2)或者由一個根結點和兩個互不相交的被稱為根的左子樹和右子樹組成。左子樹和右子樹又分別是一棵二叉樹。
特點:1. 每個結點至多只有兩棵子樹 2. 左右子樹不能顛倒(二叉樹是有序樹)。
二叉樹和度為2的有序樹的區別:
- 度為2的有序樹樹至少有3個結點,而二叉樹可以為空
- 度為2的有序樹的左右次序是相對于另一個孩子結點而言的,若某個結點只有一個孩子結點,則這個孩子結點就無須區分左右次序。而二叉樹不一樣。
幾種特殊的二叉樹
滿二叉樹
滿二叉樹:高度為h,且含有2h?12^h-12h?1個結點。每層都含有最多的結點。除了葉子結點度都為2。
特點:
- 只有最后一層有葉子結點
- 不存在度為1的結點
- 按層序從1開始編號,結點i的左孩子為2i,右孩子為2i+1;結點i的父節點為?i/2?\lfloor i/2 \rfloor?i/2?(如果有的話)
示例圖:
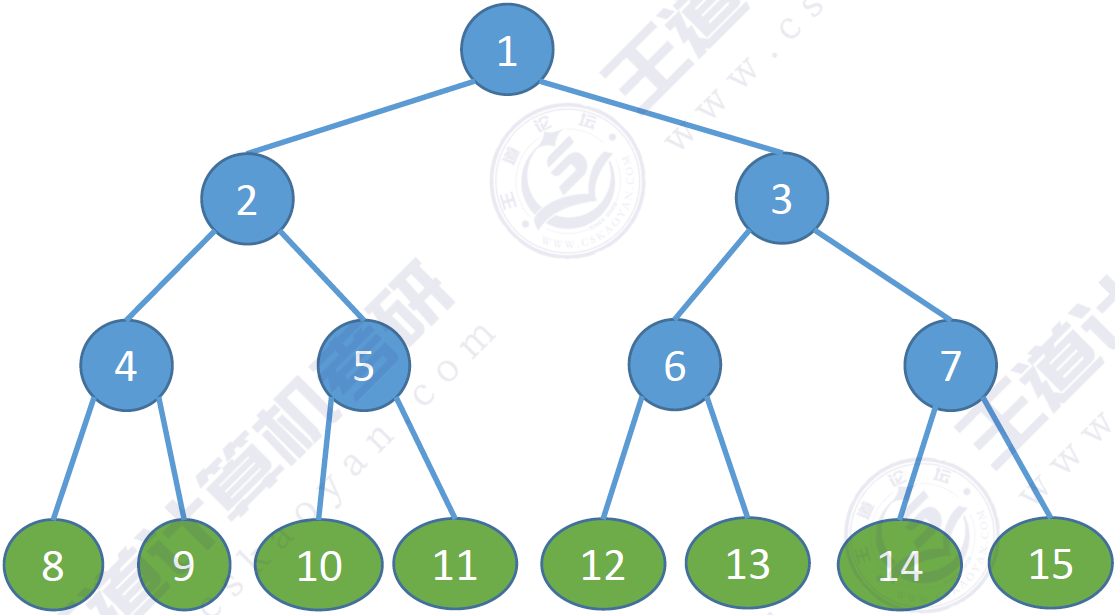
完全二叉樹
完全二叉樹:當且僅當其每個結點都與高度為h的滿二叉樹中編號為1~n的結點一一對應時,稱為完全二叉樹。
有n個結點。特點如下:
- 若 i≤?n/2?i \leq \lceil n/2 \rceili≤?n/2?,則結點 iii 為分支結點,否則為葉子結點。
- 只有最后兩層才會出現葉子結點。
- 最多只有一個度為 1 的結點(這種情況下該結點一定只有左孩子,沒有右孩子)。
- 按層序編號,若 iii 結點為葉子結點或只有左孩子,則編號大于 iii 的結點均為葉子結點。
- 同滿二叉樹的3.特點。
示例圖:
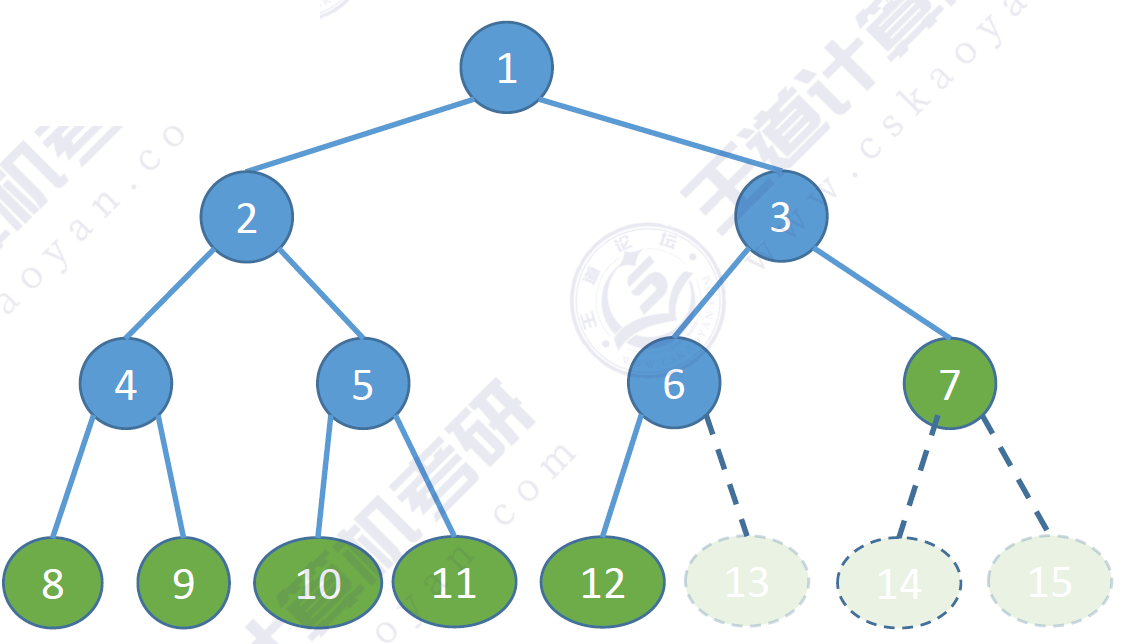
完全二叉樹可以視作從滿二叉樹中刪去若干最底層、最右邊的一些連續葉節點所得到的二叉樹。
平衡二叉樹
平衡二叉樹:任意結點的左右子樹的深度之差不超過1。詳見
二叉排序樹
二叉排序樹:左子樹上所有結點均小于根結點的關鍵字;右子樹所有結點均大于根結點的關鍵字。左子樹和右子樹個是一棵二叉排序樹。詳見
正則二叉樹
正則二叉樹:樹中每個分支都有兩個孩子,即樹中只有度為0或2的結點。
二叉樹的性質
以下推導過程略,自己推。
- 非空二叉樹的葉子結點數等于度為2的結點數加1,即n0=n2+1n_0=n_2+1n0?=n2?+1
- 非空二叉樹第i層最多有2i?12^{i-1}2i?1個結點->m叉樹第i層最多有mi?1m^{i-1}mi?1個結點
- 高度為h的二叉樹至多有2h?12^h-12h?1個結點(為一棵滿二叉樹)->高度為h的m叉樹至多有(mh?1)/(m?1)(m^h-1)/(m-1)(mh?1)/(m?1)個結點
- 具有n個結點的完全二叉樹的高度?log2(n+1)?\lceil log_2(n+1)\rceil?log2?(n+1)?或?log2n?+1\lfloor log_2n\rfloor+1?log2?n?+1
- 若完全二叉樹有2k個(偶數)個結點,則必有n1=1n_1=1n1?=1,n0=kn_0 = kn0?=k,n2=k?1n_2 = k-1n2?=k?1,若完全二叉樹有2k-1個(奇數)個結點,則必有n1=0n_1=0n1?=0,n0=kn_0=kn0?=k,n2=k?1n_2=k-1n2?=k?1(突破點:完全二叉樹最多只會有一個度為1的結點)
二叉樹的存儲結構
二叉樹的順序存儲結構
順序存儲結構:用一組地址連續的存儲單元一次自上而下、自左至右存儲完全二叉樹的結點元素。即完全二叉樹編號為i的結點元素存儲在某個數組下標為i-1的分量中。該結構對順序二叉樹和完全二叉樹比較合適。這種存儲結構要從數組下標1開始存儲數中的結點。
二叉樹的順序存儲中,一定要把二叉樹的結點編號與完全二叉樹對應起來,所以一定會有大量的空間被浪費掉。
基于以上特點如果用來存儲滿二叉樹和完全二叉樹可能使用此方法較為適合。
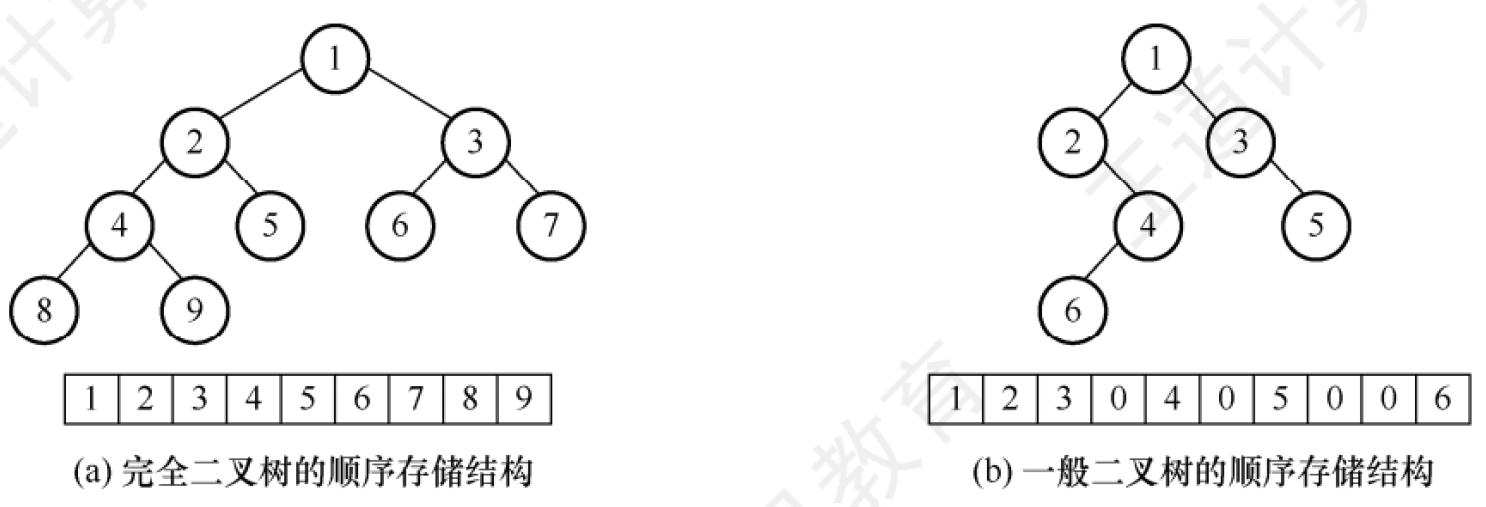
二叉樹的鏈式存儲結構
由于順序存儲的空間利用率較低,所以我們一般都會采用鏈式存儲結構。用鏈表結點來存儲二叉樹的每個結點。如圖所示一個二叉樹鏈式存儲的結點結構。

二叉樹的鏈式存儲結構描述如下:
typedef struct BiTNode {ElemType data; // 結點數據struct BiTNode *lchild, *rchild; // 左右孩子指針
} BiTNode, *BiTree;
一顆二叉樹及其所對應的二叉鏈表如圖所示,展示了鏈式存儲結構:
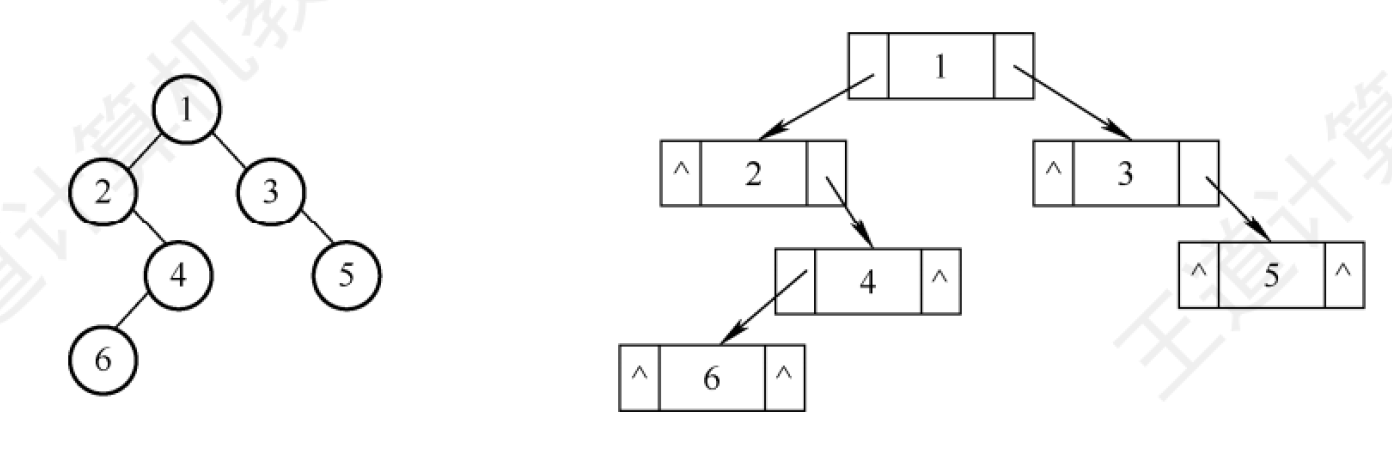
當然也很容易知道,含有n個結點的二叉鏈表中,含有n+1個空鏈域。這為后面的線索二叉樹提供了方便。
二叉樹的遍歷
先序遍歷
先序遍歷:先訪問根結點,然后先序遍歷左子樹,最后先序遍歷右子樹。
實現:
void PreOrderTraverse(BiTree T) {if (T == NULL) return; // 遞歸終止條件visit(T); // 訪問根結點PreOrderTraverse(T->lchild); // 先序遍歷左子樹PreOrderTraverse(T->rchild); // 先序遍歷右子樹
}
中序遍歷
中序遍歷:先中序遍歷左子樹,然后訪問根結點,最后中序遍歷右子樹。
實現:
void InOrderTraverse(BiTree T) {if (T == NULL) return; // 遞歸終止條件InOrderTraverse(T->lchild); // 中序遍歷左子樹visit(T); // 訪問根結點InOrderTraverse(T->rchild); // 中序遍歷右子樹
}
后序遍歷
后序遍歷:先后序遍歷左子樹,然后后序遍歷右子樹,最后訪問根結點。
實現:
void PostOrderTraverse(BiTree T) {if (T == NULL) return; // 遞歸終止條件PostOrderTraverse(T->lchild); // 后序遍歷左子樹PostOrderTraverse(T->rchild); // 后序遍歷右子樹visit(T); // 訪問根結點
}
層次遍歷
層次遍歷:從根結點開始,按層次順序訪問結點。
實現:
void LevelOrderTraverse(BiTree T) {if (T == NULL) return; // 遞歸終止條件Queue<BiTree> q;//這里需要用到一個輔助隊列q.push(T);while (!q.empty()) {BiTree node = q.front();q.pop();visit(node);if (node->lchild != NULL) q.push(node->lchild);if (node->rchild != NULL) q.push(node->rchild);}
}
這里用到了之前已經學過的[[棧和隊列#隊列]]的知識,代碼里面用到了C++的隊列,如果是書上的,那么 push就是 EnQueue,pop就是 DeQueue。
算法效率分析與改造
不管是哪種算法,每個結點都訪問一次且僅訪問一次,故時間復雜度都是O(n)。
算法改造成為非遞歸算法時,通常需要借用[[棧和隊列#棧]]一個來存儲結點。如以下中序遍歷改造所示:
// 中序遍歷非遞歸算法,需要借用一個棧
void InOrder2(BiTree T){InitStack(S); BiTree p=T; // p是遍歷指針while(p||!isEmpty(S)){if(p){Push(S,p);p=p->lchild;}else{Pop(S,p);visit(p);p=p->rchild;}}
}
利用遍歷序列構造一個二叉樹
給定先序遍歷和中序遍歷序列,可以唯一確定一棵二叉樹。先序遍歷的第一個元素是根結點,然后在中序遍歷中找到根結點的位置,左邊的部分是左子樹,右邊的部分是右子樹。
同理,給定后序遍歷和中序遍歷序列,也可以唯一確定一棵二叉樹。后序遍歷的最后一個元素是根結點,然后在中序遍歷中找到根結點的位置,左邊的部分是左子樹,右邊的部分是右子樹。
那么,給定層序和中序遍歷,也可以唯一確定一棵二叉樹。層序遍歷的第一個元素是根結點,然后在中序遍歷中找到根結點位置,左邊的部分是左子樹,右邊的部分是右子樹。
那么很顯然,先序、后序、層序倆倆組合無法唯一確定一棵二叉樹。
注:此節需要練習才能熟練掌握。
線索二叉樹
傳統的二叉樹,每個結點有兩個指針,分別指向左孩子和右孩子。不能直接得到結點在遍歷過程中的前驅和后繼結點。為了解決這個問題,引入了線索二叉樹。
在前面的內容中我們知道:在含有n個結點的二叉樹中,含有n+1個空鏈域。線索二叉樹就是利用這些空鏈域來存儲結點的前驅和后繼信息。
線索二叉樹規定:若無左子樹,令lchild指向其前驅結點;若無右子樹,令rchild指向其后繼結點。如圖所示為線索二叉樹的結點結構
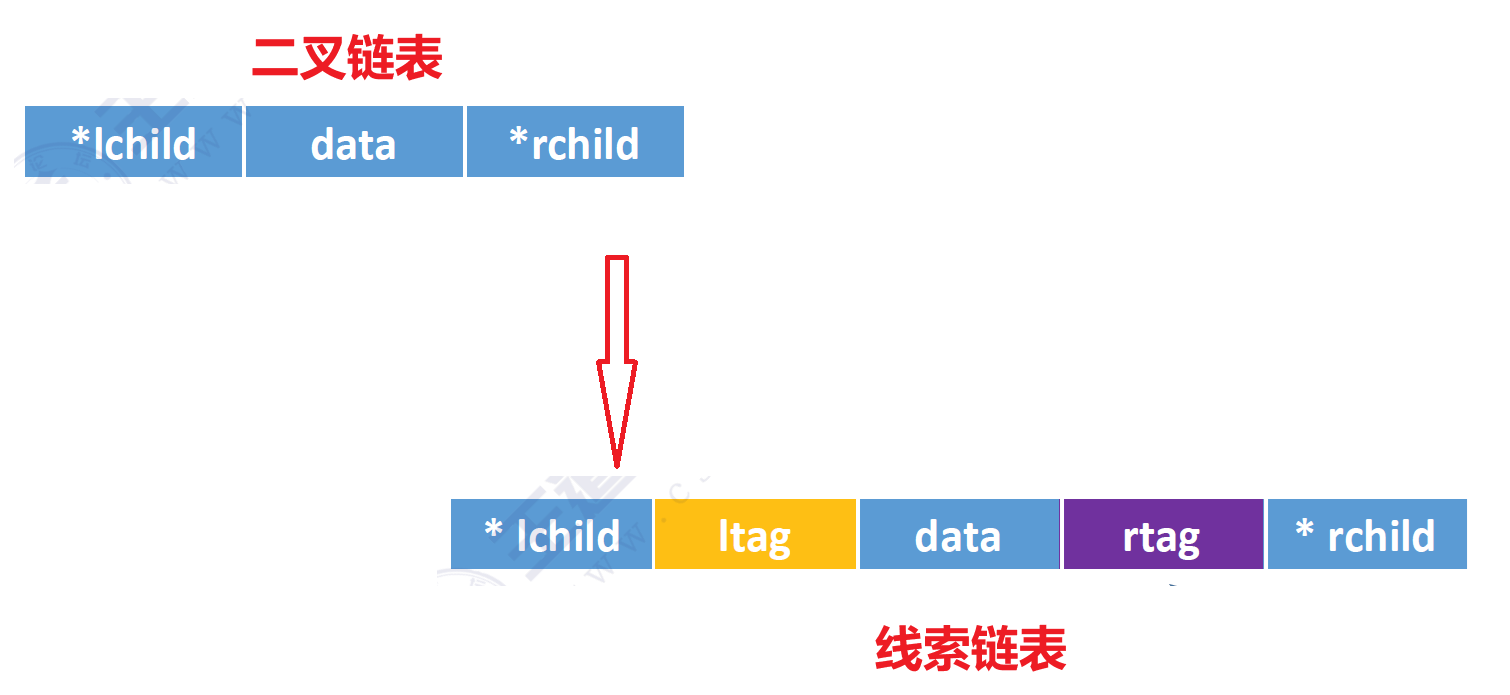
其中標志域lflag和rflag用來標識指針域是指向孩子結點還是前驅/后繼結點。
{lflag=0表示?lchild指向孩子結點lflag=1表示?lchild指向前驅結點rflag=0表示?rchild指向孩子結點rflag=1表示?rchild指向后繼結點\begin{array}{l} \left\{ \begin{aligned} &\text{lflag}=0 \text{ 表示 } lchild \text{ 指向孩子結點} \\ &\text{lflag}=1 \text{ 表示 } lchild \text{ 指向前驅結點} \\ &\text{rflag}=0 \text{ 表示 } rchild \text{ 指向孩子結點} \\ &\text{rflag}=1 \text{ 表示 } rchild \text{ 指向后繼結點} \\ \end{aligned} \right. \end{array} ?????lflag=0?表示?lchild?指向孩子結點lflag=1?表示?lchild?指向前驅結點rflag=0?表示?rchild?指向孩子結點rflag=1?表示?rchild?指向后繼結點??
那么線索二叉樹的存儲結構描述如下:
typedef struct ThreadNode {ElemType data; // 結點數據struct ThreadNode *lchild, *rchild; // 左右孩子指針int lflag, rflag; // 標志域
} ThreadNode, *ThreadTree;
線索二叉樹的構造:遍歷一次二叉樹,只是在遍歷的過程中,檢查當前結點的左右指針域是否為空,若為空,將它們改為指向前驅結點或后繼結點的線索。代碼:
// 創建中序線索二叉樹
void CreateInThread(ThreadTree T) {ThreadTree pre = NULL; // pre用于記錄當前結點的前驅if (T != NULL) {InThread(T, pre); // 對二叉樹進行中序線索化pre->rchild = NULL; // 最后一個結點的后繼線索置空pre->rtag = 1; // rtag=1表示rchild為線索}
}// 中序遍歷遞歸線索化
void InThread(ThreadTree &p, ThreadTree &pre) {if (p != NULL) {InThread(p->lchild, pre); // 遞歸線索化左子樹// 若左子樹為空,則lchild指向前驅pre,ltag=1if (p->lchild == NULL) {p->lchild = pre;p->ltag = 1;}// 若前驅結點的右子樹為空,則rchild指向當前結點,rtag=1if (pre != NULL && pre->rchild == NULL) {pre->rchild = p;pre->rtag = 1;}pre = p; // 更新前驅為當前結點InThread(p->rchild, pre); // 遞歸線索化右子樹}
}
先序線索化:
void CreatePreThread(ThreadTree T) {ThreadTree pre = NULL; // pre用于記錄當前結點的前驅if (T != NULL) {PreThread(T, pre); // 對二叉樹進行先序線索化if(pre->rchild == NULL) {//這里我有點疑問,可能他和中序線索化一樣也不是不行,因為先和中的pre->rchild一定是NULL。pre->rtag = 1; // rtag=1表示rchild為線索}}
}
// 先序遍歷遞歸線索化
void PreThread(ThreadTree p, ThreadTree &pre) {if (p != NULL) { //左子樹為空,建立線索if(p->lchild == NULL){p->lchild = pre;p->ltag = 1;}if(pre != NULL && pre->rchild == NULL){pre->rchild = p;pre->rtag = 1;}pre = p;//我們前面介紹過,如果p的左子樹為空,則建立p為左孩子,所以判斷p的左子樹代表的是否為線索if(p->ltag == 0) {PreThread(p->lchild, pre); // 遞歸線索化左子樹}PreThread(p->rchild, pre); // 遞歸線索化右子樹}
}
后序線索化:
void CreatePostThread(ThreadTree T) {ThreadTree pre = NULL; // pre用于記錄當前結點的前驅if (T != NULL) {PostThread(T, pre); // 對二叉樹進行后序線索化if(pre->rchild == NULL) {pre->rtag = 1; // rtag=1表示rchild為}}
}
// 后序遍歷遞歸線索化
void PostThread(ThreadTree p, ThreadTree &pre) {if (p != NULL) {PostThread(p->lchild, pre);PostThread(p->rchild, pre);if (p->lchild == NULL) {p->ltag = 1;p->lchild = pre; // 左子樹為空,建立線索}if (pre != NULL && pre->rchild == NULL) {pre->rtag = 1;pre->rchild = p;}pre=p;}
}
帶有頭結點的線索二叉樹
如圖(此為中序):
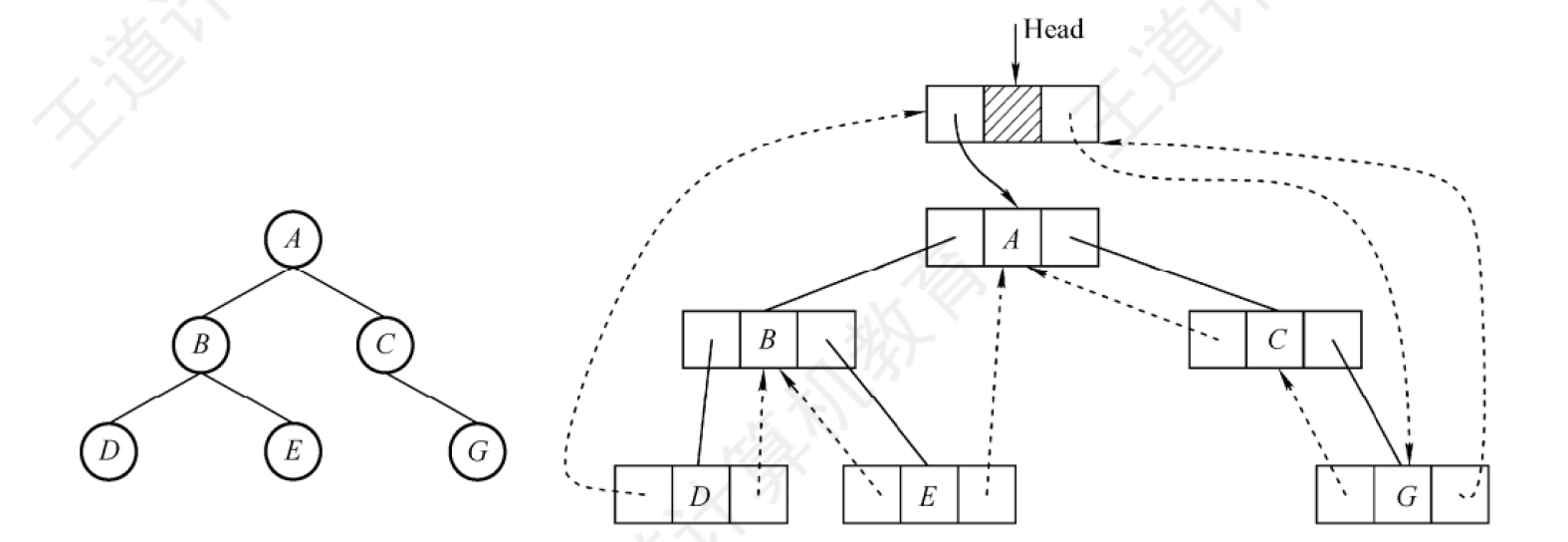
他的指向關系在圖中很明確,這樣做的好處就是能夠很方便的從前往后或者從后往前對線索二叉樹進行一個遍歷。
線索二叉樹的遍歷
線索二叉樹的遍歷:利用線索二叉樹,可以實現二叉樹遍歷的非遞歸算法。
以中序遍歷找后繼為例,代碼如下:
void Inorder(ThreadNode *T) {for (ThreadNode *p = Firstnode(T); p != NULL; p = Nextnode(p))visit(p); // 訪問結點
}
ThreadNode *Firstnode(ThreadNode *p) {while (p->ltag == 0) p = p->lchild; //找到最左下結點return p;
}
ThreadNode *Nextnode(ThreadNode *p) {if (p->rtag == 0) return Firstnode(p->rchild);else return p->rchild; // 返回后繼結點
}
對于中序線索二叉樹的遍歷,可以使用上述的實現方式,只需變化一些條件,具體可以練習。
對于先序和后序線索二叉樹的遍歷,類似的實現方式也可以使用。
樹和森林
樹的存儲結構
雙親表示法
采用一組連續空間來存儲每個結點,同時每個結點中增設一個偽指針,指示其雙親結點在數組中的位置。可以很快得到每個結點的雙親結點,但求結點的孩子時需要遍歷整個結構。
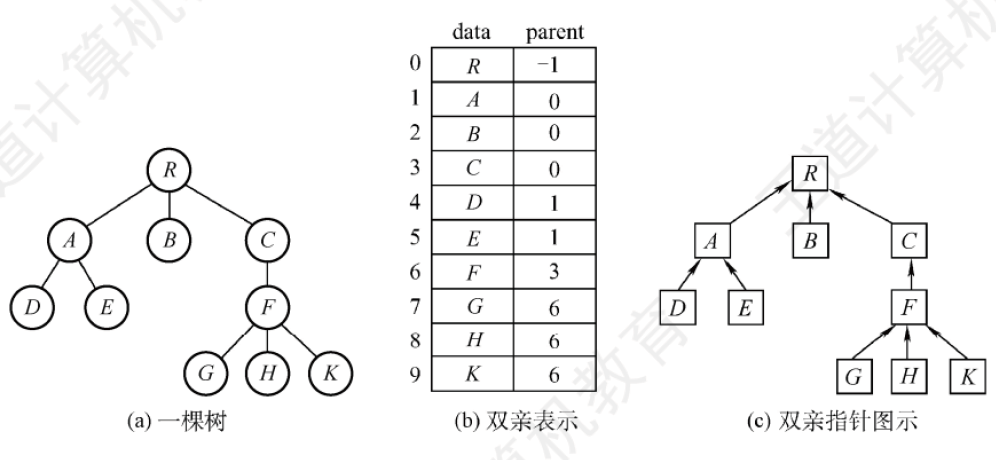
存儲結構描述:
#define MAX_TREE_SIZE 100 // 定義樹的最大結點數
typedef struct {ElemType data; // 結點數據int parent; // 雙親結點的下標
} PTNode; // 雙親結點結構
typedef struct {PTNode nodes[MAX_TREE_SIZE]; // 存儲結點的數組int n; // 結點數
} PTree; // 雙親表示法的樹結構
雙親表示法表示一個森林:每棵樹的根節點雙親指針= -1
孩子表示法
將每個結點的孩子結點都用單鏈表連接起來形成一個線性結構,n個結點就有n個孩子鏈表。尋找子女操作非常直接,而尋找雙親需要遍歷n個結點中孩子鏈表指針域所指向的n個孩子鏈表
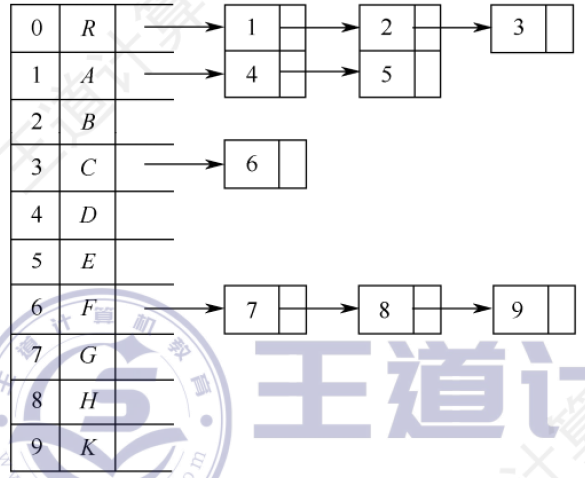
孩子表示法表示一個森林:用孩子表示法存儲森林,需要記錄多個根的位置
孩子兄弟表示法
又稱二叉樹表示法,即以二叉鏈表作為樹的存儲結構。每個結點分為三部分:結點值、指向結點第一個孩子節點的指針,指向結點下一個兄弟結點的指針。優點是可以方便地實現樹轉換為二叉樹的操作,易于查找結點的孩子等。缺點是查找雙親麻煩
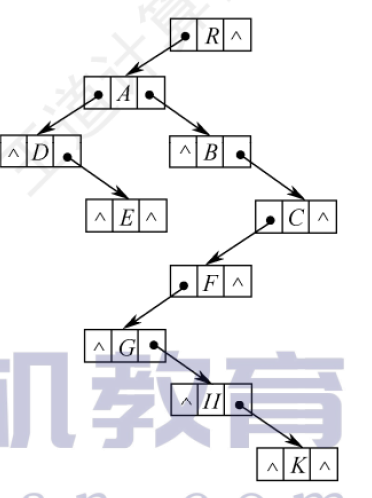
存儲結構描述:
typedef struct CSNode {ElemType data; // 結點數據struct CSNode *firstchild; // 指向第一個孩子結點的指針struct CSNode *nextsibling; // 指向下一個兄弟結點的指針
} CSNode, *CSTree; // 孩子兄弟表示法
樹、森林轉化成二叉樹
樹轉換為二叉樹的規則:每個結點左指針指向它的第一個孩子結點,右指針指向它在樹中相鄰的兄弟節點,“左孩子右兄弟”,由樹轉換的二叉樹沒有右子樹。
森林轉換為二叉樹:先將森林中的每棵樹轉換為二叉樹,把第一棵樹的根作為轉換后二叉樹的根,其左子樹作為左子樹。第二棵樹作為轉換后的右子樹,第三棵樹作為轉換后右子樹的右子樹,即向右拼接。
二叉樹轉換為森林/樹的規則:反過來即可。將右子樹挨個拆下來。二叉樹轉換為樹或森林是唯一的。
樹和森林的遍歷
樹和森林遍歷與二叉樹遍歷之前的對應關系
| 樹 | 森林 | 二叉樹 |
|---|---|---|
| 先根遍歷 | 先序遍歷 | 先序遍歷 |
| 后根遍歷 | 后序遍歷 | 中序遍歷 |
樹與二叉樹的應用
哈夫曼樹和哈夫曼編碼
結點的權:有某種現實含義的數值(如:表示結點的重要性等)
結點的帶權路徑長度:從樹的根到該結點的路徑長度(經過的邊數)與該結點上權值的乘積
樹的帶權路徑長度:樹中所有葉結點的帶權路徑長度之和(WPL, Weighted Path Length)
WPL=∑i=1nwi?liWPL=\sum_{i=1}^{n} w_i \cdot l_iWPL=i=1∑n?wi??li?
在含有n個帶權葉節點的二叉樹中,其中帶權路徑長度(WPL)最小的二叉樹稱為哈夫曼樹(Huffman Tree),也稱為最優二叉樹。
例題:
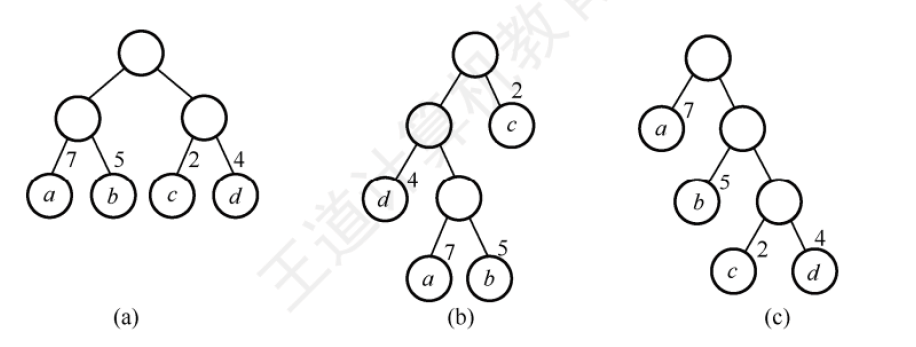
由此算得:
WPLa=7?2+5?2+2?2+4?2=36WPL_a=7*2+5*2+2*2+4*2=36WPLa?=7?2+5?2+2?2+4?2=36
WPLb=7?3+5?3+2?1+4?2=46WPL_b=7*3+5*3+2*1+4*2=46WPLb?=7?3+5?3+2?1+4?2=46
WPLc=7?1+5?2+2?3+4?3=35WPL_c=7*1+5*2+2*3+4*3=35WPLc?=7?1+5?2+2?3+4?3=35(哈夫曼樹)
構造方式:簡單說,從結點中選出兩個最小的結點,構成一個新節點,權為兩結點之和,重復直到所有結點都處理完畢。
哈夫曼編碼就是左0右1,那么a=0 ;b=10;c=110;d=111。
哈夫曼編碼的特點是:沒有一個編碼是另一個編碼的前綴,這樣可以保證編碼的唯一性。
并查集
并查集的概念及其實現
并查集是一種簡單的集合表示,它支持以下操作:Initialize(初始化)、Find(查找)、Union(合并)。
并查集的存儲結構
通常用樹的雙親表示作為并查集的存儲結構,每個子集合以一棵樹表示。多說無益,直接看示意圖:
假設有一個S={0,1,2,3,4,5,6,7,8,9,10},初始化他們都是一個個的幾個,每個子集合的數組值為-1。
初始表示:
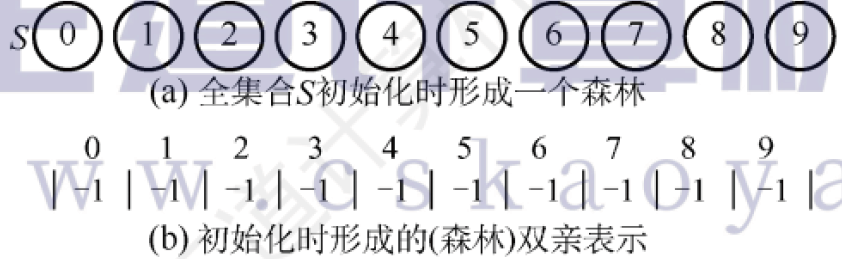
經過系列計算以后,他們合并成為了三個集合:S1={0,6,7,8}S_1=\{0,6,7,8\}S1?={0,6,7,8}、S2={1,4,9}S_2=\{1,4,9\}S2?={1,4,9}、S3={2,3,5}S_3=\{2,3,5\}S3?={2,3,5}
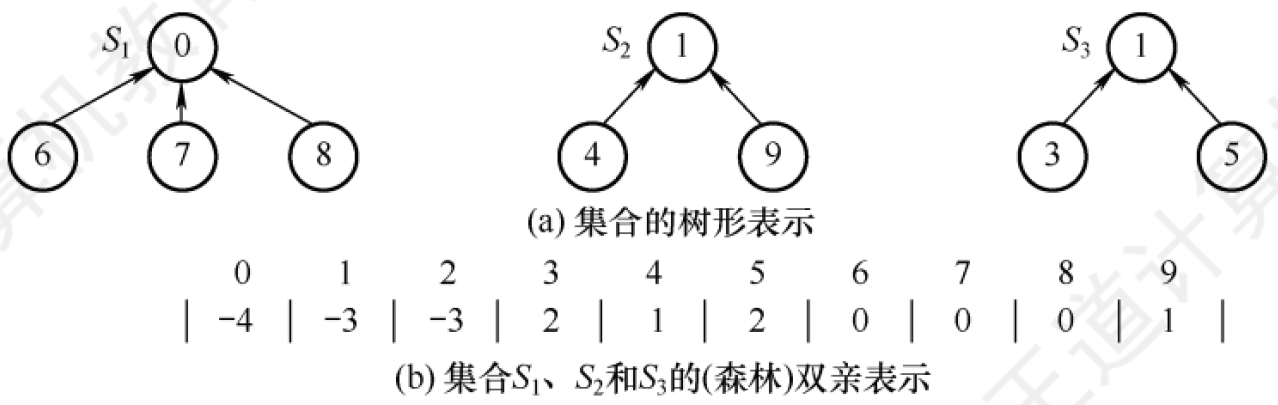
又計算,想把S1S_1S1?和S2S_2S2?合并

結束,很一目了然的并查集
并查集操作的基本實現
#define MAX_SIZE 100 // 并查集的最大大小
int UFSets[MAX_SIZE];// 并查集數組(雙親表示法)
//初始化
void InitUFSets()
{for (int i = 0; i < MAX_SIZE; i++) UFSets[i] = -1; // 每個元素初始化為-1,表示每個元素都是一個獨立的集合
}
//Find 找到集合的根元素
int Find(int x)
{while (UFSets[x] >= 0) x = UFSets[x];return x;
}
//Union 合并兩個集合
void Union(int Root1, int Root2)
{if (Root1 != Root2) {//要求Root1和Root2是不同的集合UFSets[Root2] = Root1; // 將Root2的根元素指向Root1,表示合并}
}
注意:本代碼并沒有傳遞數組參數,因為只是一整個代碼,已經放在全局變量中,遇到題目需要自行分析。
復雜度分析:Find操作的時間復雜度為O(d)O(d)O(d)(d為樹深度),Union操作的時間復雜度為O(1)。
并查集之優化
//改進后的Union
void Union(int Root1, int Root2) {if(Root1 != Root2) { //要求Root1和Root2是不同的集合if (UFSets[Root1] < UFSets[Root2]) { // Root1的集合更大UFSets[Root1] += UFSets[Root2]; // 更新Root1的大小UFSets[Root2] = Root1; // 將Root2的根元素指向Root1} else {UFSets[Root2] += UFSets[Root1]; // 更新Root2的大小UFSets[Root1] = Root2; // 將Root1的根元素指向Root2}}
}
//改進后的Find,目的在于壓縮路徑,只要是根的元素,就把他掛在根元素上。
int Find(int x) {int root = x;while(UFSets[root] >= 0) {root = UFSets[root]; // 找到根元素}while(x!=root){int temp = UFSets[x]; // 臨時存儲當前元素的父節點UFSets[x] = root; // 路徑壓縮,將當前元素直接指向根元素x = temp; // 移動到下一個元素}return root;
}

)







:軟件信息展示)
![[HDLBits] Cs450/gshare](http://pic.xiahunao.cn/[HDLBits] Cs450/gshare)
![[學習] 雙邊帶調制 (DSB) 與單邊帶調制 (SSB) 深度對比](http://pic.xiahunao.cn/[學習] 雙邊帶調制 (DSB) 與單邊帶調制 (SSB) 深度對比)



:three states)



