嘿，各位技術潮人！好久不見甚是想念。生活就像一場奇妙冒險，而編程就是那把超酷的萬能鑰匙。此刻，陽光灑在鍵盤上，靈感在指尖跳躍，讓我們拋開一切束縛，給平淡日子加點料，注入滿滿的passion。準備好和我一起沖進代碼的奇幻宇宙了嗎？Let's go！

我的博客：yuanManGan

我的專欄：C++入門小館?C言雅韻集?數據結構漫游記? 閑言碎語小記坊?題山采玉?領略算法真諦

紅黑樹的介紹

紅黑樹也是一棵平衡二叉樹，我們之前實現的AVL樹，他是通過多次的旋轉而得到的平衡，付出了相應的代價，讓平衡因子的絕對值小于2，才使我們二叉樹的高度實現了log n,而我們的紅黑樹要求最長路徑不超過最短路徑的兩倍，通過一下條件來實現：

1.每個節點不是紅色就是黑色，

2.根節點是黑色的

3.每條路徑的黑色節點數相同

4.不存在連續的紅色節點

我們就通過這些條件來實現最長路徑不超過最短路徑的兩倍

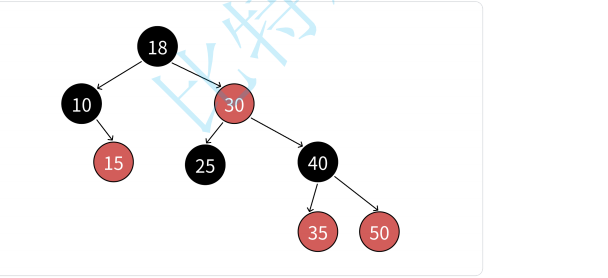
注意我們的完整的一條路徑是到左右子樹為空的路徑

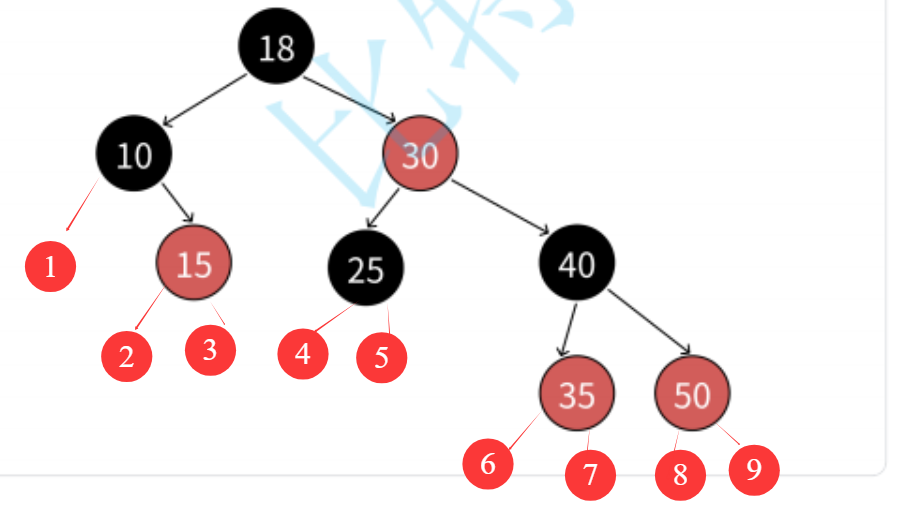
像這樣的一棵樹他的路徑數就是9條。

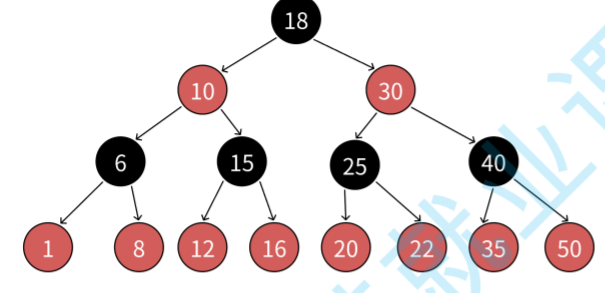
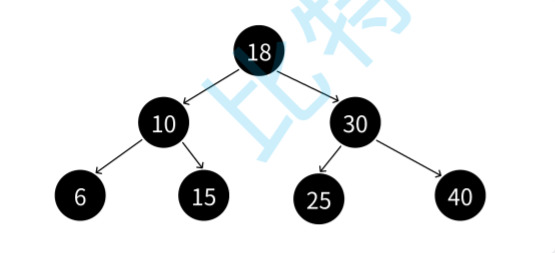
紅?樹如何確保最?路徑不超過最短路徑的2倍的？

由規則3可知，從根到NULL結點的每條路徑都有相同數量的??結點所以極端場景下，最短路徑 就就是全是??結點的路徑，假設最短路徑?度為bh(black height)

由規則2和4可知，任意?條路徑不會有連續的紅?結點，所以極端場景下，最?的路徑就是? ??紅間隔組成，那么最?路徑的?度為2*bh。

綜合紅?樹的4點規則??，理論上的全?最短路徑和???紅的最?路徑并不是在每棵紅?樹都 存在的。假設任意?條從根到NULL結點路徑的?度為x，那么bh <= h <= 2*bh。

紅?樹的效率：

假設N是紅?樹樹中結點數量，h最短路徑的?度，那么 , 由此推出 ，也就是意味著紅?樹增刪查改最壞也就是?最?路徑 ，那么時間復雜度還是 。 2^?h ? 1 <= N < 2 ^(2?h) ? 1

h ≈ logN 也就是意味著紅?樹增刪查改最壞也就是?最?路徑2 ? logN ，那么時間復雜度還是 O(logN)。

紅?樹的結構

#pragma once
enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _parent;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _left;Colour _col;RBTreeNode(const pair<K, V>& kv): _kv(kv), _right(nullptr), _left(nullptr), _col(BLACK){}
};
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;public:
private:Node* _root = nullptr;
};

紅?樹的插?

我們的插入過程的前半部分和二叉搜索樹的過程基本一樣，先找到插入的位置插入后，進行平衡調整。

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv)cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;
}

我們再來想想如果我們要插入一個節點，我們該插入紅色節點還是黑色節點呢？我們要保證每個路徑的黑色節點數相同，如果我們插入黑色節點的話我們就得讓別的路徑的黑色節點都加一才行，所以我們最好插入紅色節點，如果我們插入的節點的位置的父節點是黑色的就萬事大吉，不用進行操作了。

那遇到了父親為紅色節點時我們就得進行變色操作了，

情況1：

p為紅，那么因為p為紅那么g就不可能為紅，這里只有u是未知的，假如u為紅時，我們就得將p和u都變成黑色，然后讓g變成紅，然后繼續向上更新答案，直到更新為parent節點為空或者為黑的時候就結束。

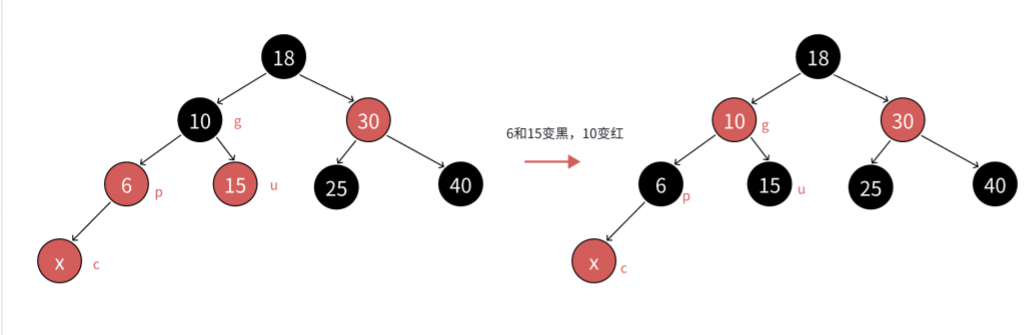
這是我們這種情況的抽象圖：

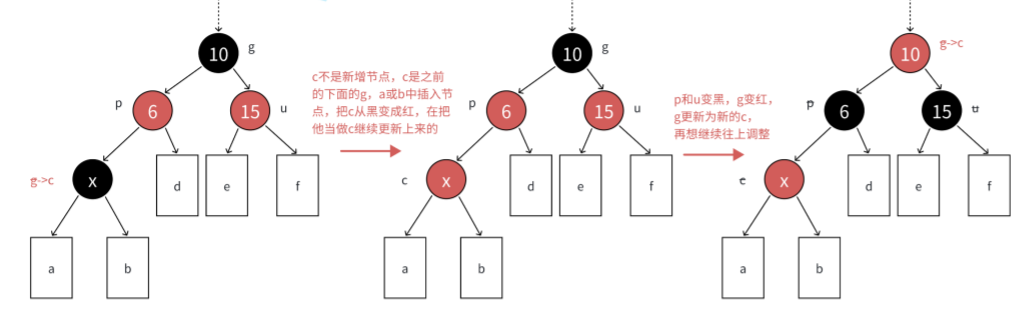
?情況二：單旋+變?

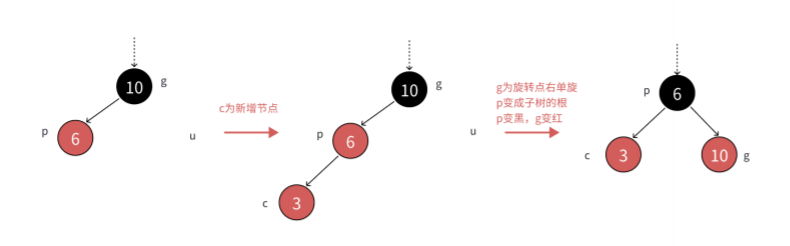
當我們往一個紅色節點的左邊插入節點時，此時g的右節點為空或者時黑色，我們不能像剛剛那樣操作了，如果我們像那樣操作，我們沒有u節點，然后操作后g的右支路的黑色節點數會多一個我們就需要將g節點進行右旋操作，讓p節點成為c和g節點的根節點。

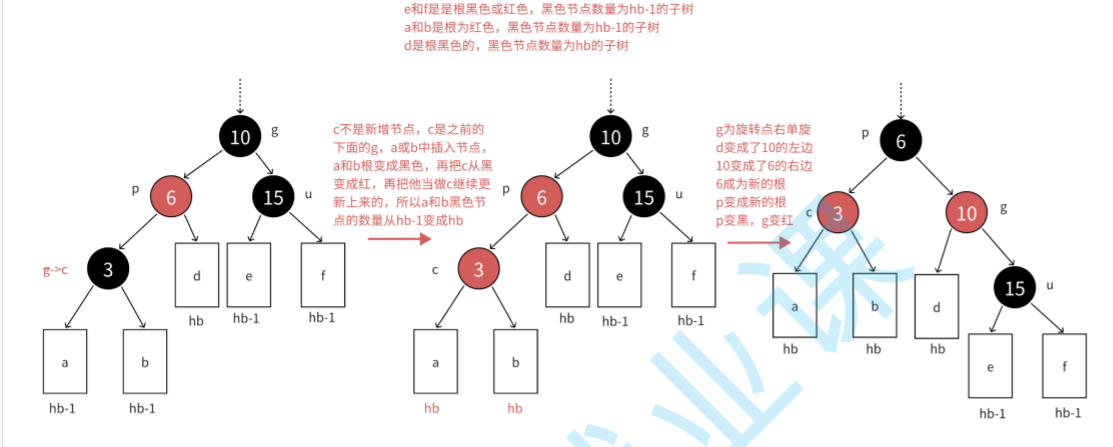
情況三：雙旋加變色：

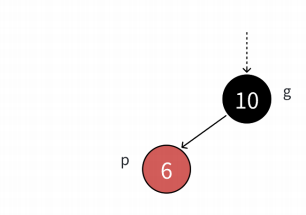
我們往這個樹的p位置的右孩子插入一個節點時就變成了

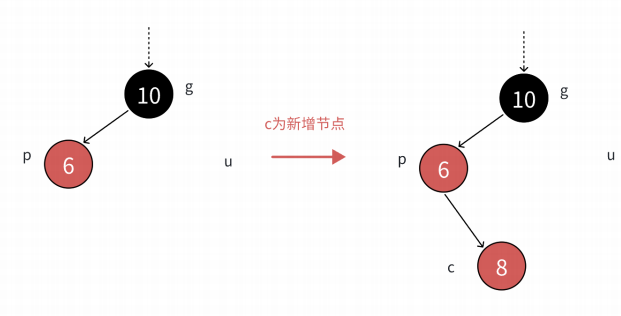
我們得先對p節點進行右旋操作就成了：

?

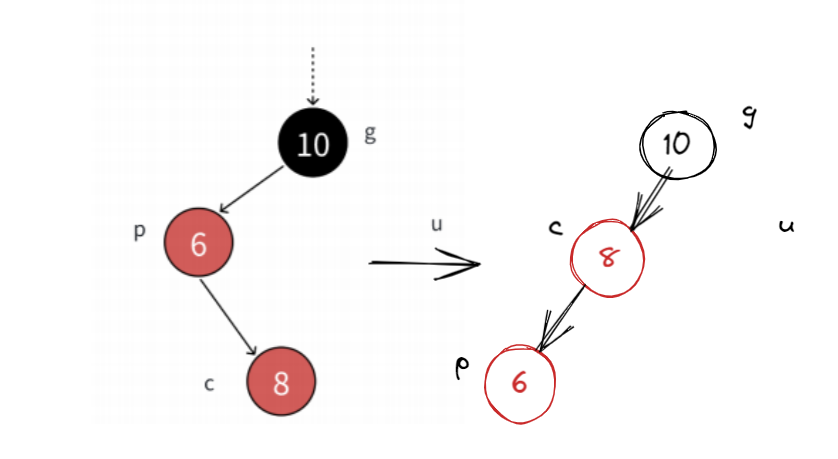
這個樣子就比較熟悉了，我們再右旋g變個色就解決了。

?

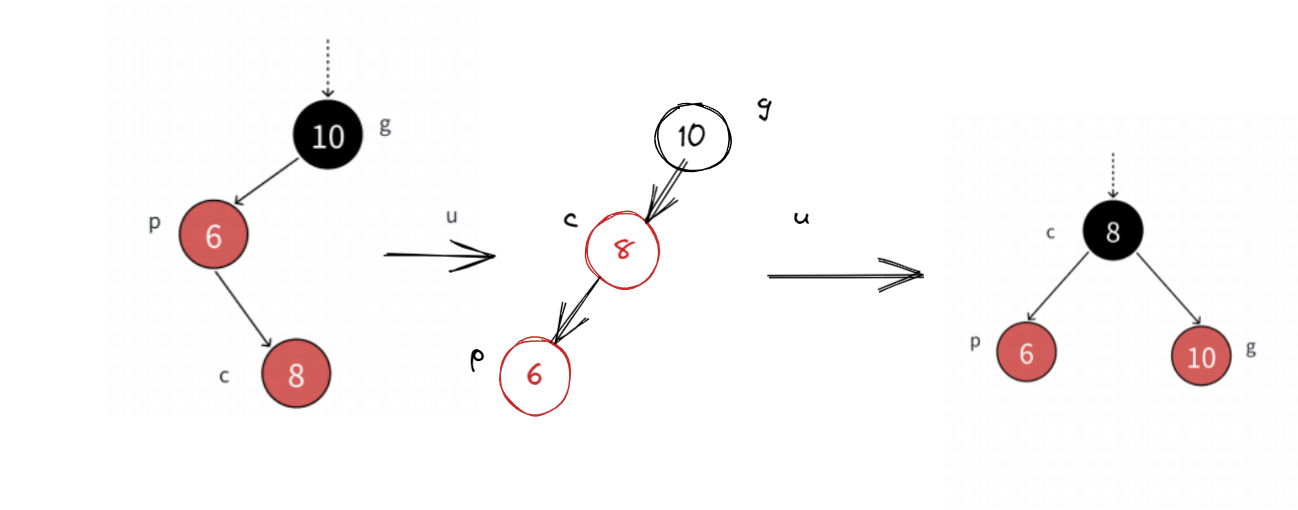
同樣的思路，當u存在且為黑時也是一樣的解決方法。

插入完整的代碼如下：

	bool Insert(const pair<K, V>& kv){if (_root == nullptr)  // 新增：處理根節點為空{_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;//插入操作while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{//插入失敗return false;}}//新插入紅色節點cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}elseparent->_left = cur;cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//1.u存在且為紅if (uncle && uncle->_col == RED){//變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//繼續往上處理cur = grandfather;parent = cur->_parent;}else{//     g//   p   u// cif (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//   p   u//     cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else // (parent == grandfather->_right){Node* uncle = grandfather->_left;//1.u存在且為紅if (uncle && uncle->_col == RED){//變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//繼續往上處理cur = grandfather;parent = cur->_parent;}else{//     g//   u   p//          cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//   u   p//     cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}