【每日算法】專題十三_隊列 + 寬搜(bfs)

1. 算法思路

BFS 算法核心思路

BFS（廣度優先搜索）使用? 隊列（Queue）按層級順序遍歷圖或樹的節點。以下是 C++ 實現的核心思路和代碼模板：

算法框架

#include <queue>
#include <vector>
#include <unordered_set>  // 用于圖的去重// 樹的 BFS 層序遍歷
vector<vector<int>> bfs(TreeNode* root) {vector<vector<int>> result;if (!root) return result;queue<TreeNode*> q;q.push(root);  // 根節點入隊while (!q.empty()) {int level_size = q.size();  // 當前層的節點數vector<int> current_level;// 處理當前層的所有節點for (int i = 0; i < level_size; i++) {TreeNode* node = q.front();q.pop();  // 隊首出隊current_level.push_back(node->val);// 將子節點入隊if (node->left) q.push(node->left);if (node->right) q.push(node->right);}result.push_back(current_level);  // 添加當前層到結果}return result;
}

關鍵點

隊列操作：
- push()：將節點加入隊尾
- front()：獲取隊首元素
- pop()：移除隊首元素
- empty()：判斷隊列是否為空
層級控制：
- 通過?level_size?記錄當前層的節點數，確保每層節點被單獨處理。
圖的 BFS（需去重）：

void graphBFS(vector<vector<int>>& graph, int start) {queue<int> q;unordered_set<int> visited;q.push(start);visited.insert(start);while (!q.empty()) {int node = q.front();q.pop();// 處理當前節點cout << node << " ";// 遍歷所有鄰接節點for (int neighbor : graph[node]) {if (visited.find(neighbor) == visited.end()) {visited.insert(neighbor);q.push(neighbor);}}}
}

應用場景

二叉樹層序遍歷
無權圖最短路徑

int shortestPath(vector<vector<int>>& graph, int start, int target) {queue<pair<int, int>> q;  // {節點, 距離}unordered_set<int> visited;q.push({start, 0});visited.insert(start);while (!q.empty()) {auto [node, dist] = q.front();q.pop();if (node == target) return dist;for (int neighbor : graph[node]) {if (!visited.count(neighbor)) {visited.insert(neighbor);q.push({neighbor, dist + 1});}}}return -1;  // 無法到達
}

狀態擴展問題（如迷宮）

總結

隊列選擇：C++ 中使用?std::queue?或?std::deque。
去重機制：圖的 BFS 必須用?unordered_set?避免重復訪問。
層級處理：通過記錄每層節點數實現逐層遍歷。

2. 例題

2.1 N 叉數的層序遍歷

429. N 叉樹的層序遍歷 - 力扣（LeetCode）

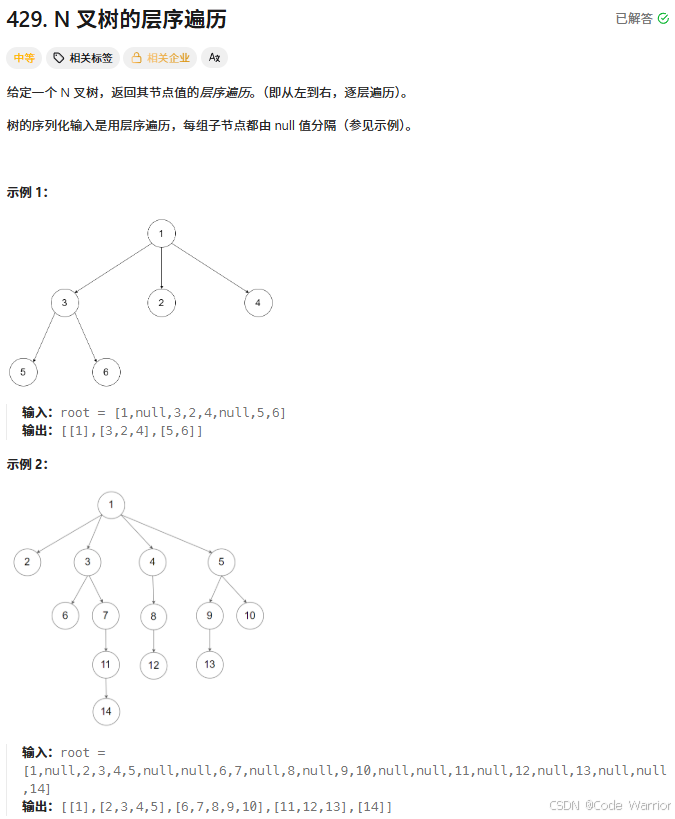
核心思路：隊列驅動的層序遍歷

這段代碼實現了?N 叉樹的層序遍歷，核心思路是利用隊列的?FIFO（先進先出）特性?逐層處理節點。具體步驟如下：

初始化隊列：將根節點放入隊列。
循環處理每一層：
- 記錄當前層節點數?sz（即隊列當前長度）。
- 創建當前層的臨時數組?tmp。
- 遍歷當前層所有節點：
  - 從隊列取出節點，將值加入?tmp。
  - 將該節點的所有子節點依次入隊（確保下一層節點被加入隊列尾部）。
- 將當前層結果?tmp?加入最終結果?ret。
返回結果：當隊列為空時，所有層處理完畢。

關鍵點

層級控制：通過?sz?鎖定當前層的節點數，確保每次循環處理完一層的所有節點。
隊列的作用：
- 出隊：處理當前層的節點。
- 入隊：按順序存儲下一層的節點。
適用于 N 叉樹：通過?children?數組處理任意數量的子節點。

復雜度分析

時間復雜度：O (n)，每個節點僅入隊 / 出隊一次。
空間復雜度：O (n)，最壞情況下隊列同時存儲一層的所有節點（例如滿二叉樹的最后一層）。

    vector<vector<int>> levelOrder(Node* root) {vector<vector<int>> ret;queue<Node*> q;if(root == nullptr) return ret;q.push(root);while(q.size()){int sz = q.size();vector<int> tmp;for(int i = 0; i < sz; ++i){Node* t = q.front();q.pop();tmp.push_back(t->val);for(Node* child : t->children)q.push(child);}ret.push_back(tmp);}return ret;}

2.2 二叉樹的鋸齒層序遍歷

103. 二叉樹的鋸齒形層序遍歷 - 力扣（LeetCode）

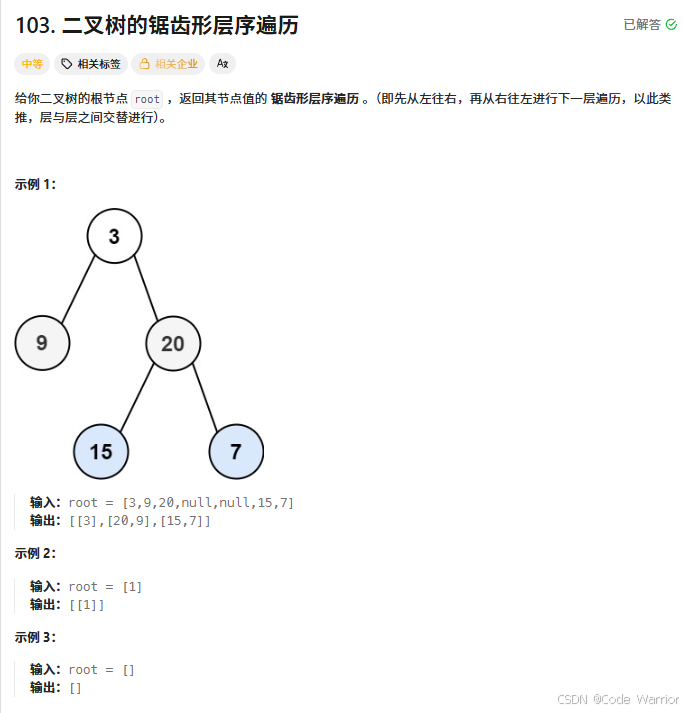
核心思路：基于隊列的 zigzag 層序遍歷（之字形遍歷）

這段代碼實現了二叉樹的?之字形層序遍歷（即相鄰層的節點順序相反：第一層從左到右，第二層從右到左，第三層再從左到右，以此類推），核心思路是利用?隊列控制層級?+?雙端隊列（deque）控制每層順序。具體步驟如下：

初始化隊列：將根節點入隊，用?flag?標記當前層的遍歷方向（初始為?true，表示從左到右）。
循環處理每一層：
- 記錄當前層節點數?sz（鎖定當前層的節點范圍）。
- 創建雙端隊列?tmp（支持頭部和尾部插入，靈活控制順序）。
- 遍歷當前層所有節點：
  - 從隊列取出節點。
  - 根據?flag?決定插入方向：
    - flag = true?時，從尾部插入（push_back），保持左到右順序。
    - flag = false?時，從頭部插入（push_front），實現右到左順序。
  - 將節點的左右子節點依次入隊（確保下一層節點按正常順序存儲）。
- 轉換并保存當前層結果：將?tmp?轉為?vector<int>?后加入最終結果?ret。
- 翻轉方向標記：flag = !flag，下一層使用相反順序。
返回結果：隊列為空時，所有層處理完畢。

關鍵點

隊列的作用：控制層級順序，確保按層依次處理節點（與普通層序遍歷一致）。
雙端隊列的作用：通過頭部 / 尾部插入，在不改變子節點入隊順序的前提下，靈活反轉當前層的輸出順序。
方向標記?flag：切換相鄰層的遍歷方向，實現 “之字形” 效果。

復雜度分析

時間復雜度：O (n)，每個節點僅入隊 / 出隊一次，雙端隊列的插入操作是 O (1)。
空間復雜度：O (n)，隊列和雙端隊列最多同時存儲一層的所有節點。

    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {vector<vector<int>> ret;queue<TreeNode*> q;if(root == nullptr) return ret;q.push(root);bool flag = true;while(q.size()){int sz = q.size();deque<int> tmp;for(int i = 0; i < sz; ++i){TreeNode* t = q.front();q.pop();if(flag) // 左向右tmp.push_back(t->val);else // 右向左tmp.push_front(t->val);if(t->left)q.push(t->left);if(t->right)q.push(t->right);}ret.push_back(vector<int>{tmp.begin(), tmp.end()});flag = !flag;} return ret;}

2.3 二叉樹最大寬度

662. 二叉樹最大寬度 - 力扣（LeetCode）

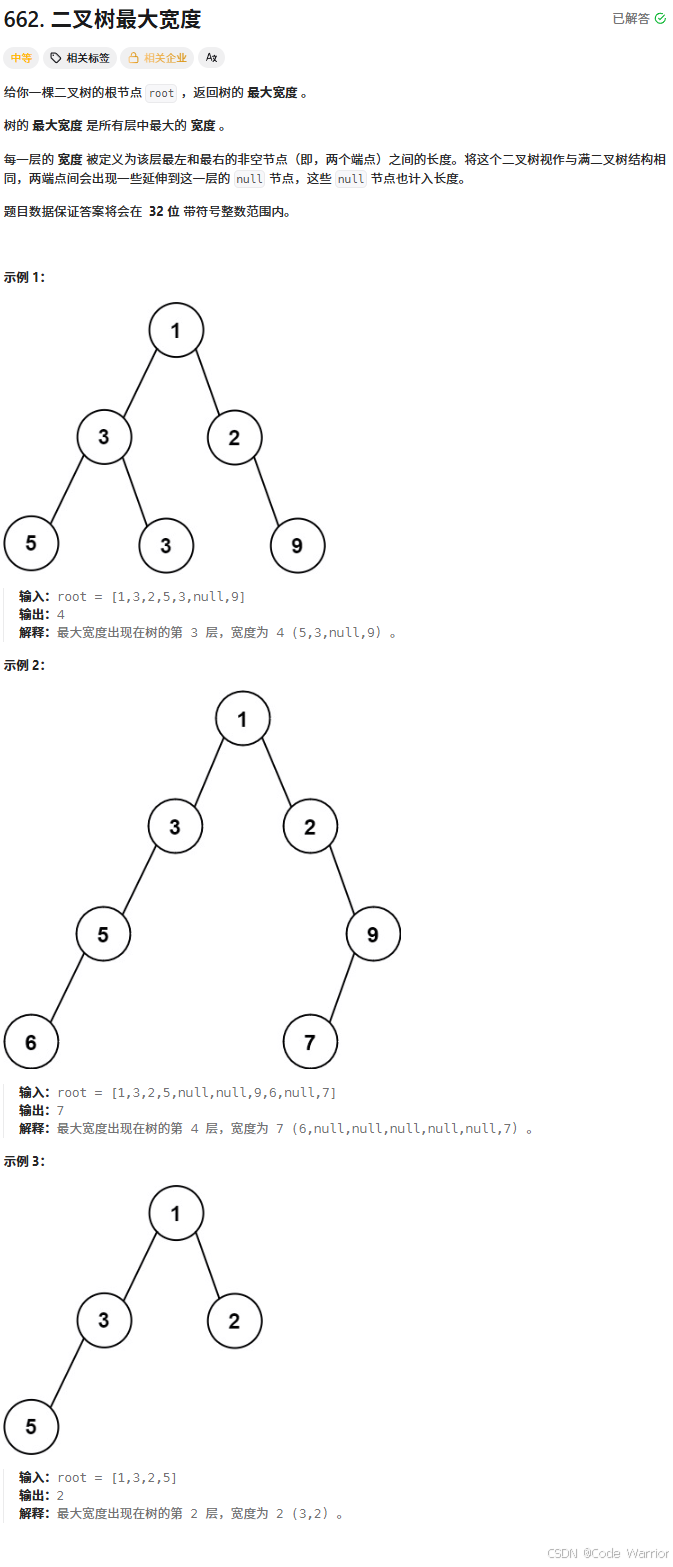
核心思路：二叉樹最大寬度計算（層序遍歷 + 節點編號）

這段代碼實現了計算二叉樹的最大寬度（即任意層的最左節點和最右節點之間的跨度，包含空節點），核心思路是通過層序遍歷 + 節點編號來確定每層的寬度。具體步驟如下：

隊列初始化：用?vector<pair<TreeNode*, unsigned int>>?存儲節點及其編號（根節點編號為?0）。編號規則為：若父節點編號為?x，則其左子節點編號為?2x，右子節點編號為?2x+1。
循環處理每一層：
- 計算當前層寬度：當前層的寬度為隊列中首尾節點的編號之差 + 1（即?x2 - x1 + 1），更新全局最大寬度?ret。
- 生成下一層節點：遍歷當前層所有節點，將每個節點的子節點（若存在）及其編號加入臨時隊列?tmp：
  - 左子節點：編號為?2 * x
  - 右子節點：編號為?2 * x + 1
- 更新隊列：用臨時隊列?tmp?替換當前隊列?q，進入下一層循環。
返回結果：遍歷完所有層后，ret?即為二叉樹的最大寬度。

關鍵點

節點編號：通過編號計算每層寬度，避免直接統計節點數（處理空節點的關鍵）。
層序遍歷：確保按層處理節點，計算每層的首尾跨度。
容器選擇：
- 方法一：用?vector?存儲每層節點，遍歷后整體替換（更高效）。
- 方法二：用?erase?刪除隊首元素（性能較差，因?vector?的頭部刪除是 O (n)）。
數據類型：使用?unsigned int?避免編號溢出（某些極端二叉樹的編號可能非常大）。

復雜度分析

時間復雜度：O (n)，每個節點僅處理一次。
空間復雜度：O (n)，隊列最多存儲一層的所有節點。

    int widthOfBinaryTree(TreeNode* root) {int ret = 0;vector<pair<TreeNode*, unsigned int>> q; // 用vector可以進行下標訪問，取第一個和最后一個數if(root == nullptr) return ret;q.push_back({root, 0});while(q.size()){// 計算每層的最大寬度auto& [y1, x1] = q[0];auto& [y2, x2] = q.back();ret = max(ret, (int)(x2 - x1 + 1));// 層序遍歷// 法一vector<pair<TreeNode*, unsigned int>> tmp;for(auto& [y3, x3] : q){if(y3->left)tmp.push_back({y3->left, 2 * x3});if(y3->right)tmp.push_back({y3->right, 2 * x3 + 1});}// 法二，注意的是頻繁的頭部刪除應該選用deque做容器n(1)//int sz = q.size();// while(sz--)// {//     auto [y3, x3] = q[0];//     q.erase(q.begin());//     if(y3->left)//         q.push_back({y3->left, 2 * x3});//     if(y3->right)//         q.push_back({y3->right, 2 * x3 + 1});// }q = tmp;}return ret;}

2.4 在每個樹行中找最大值

515. 在每個樹行中找最大值 - 力扣（LeetCode）

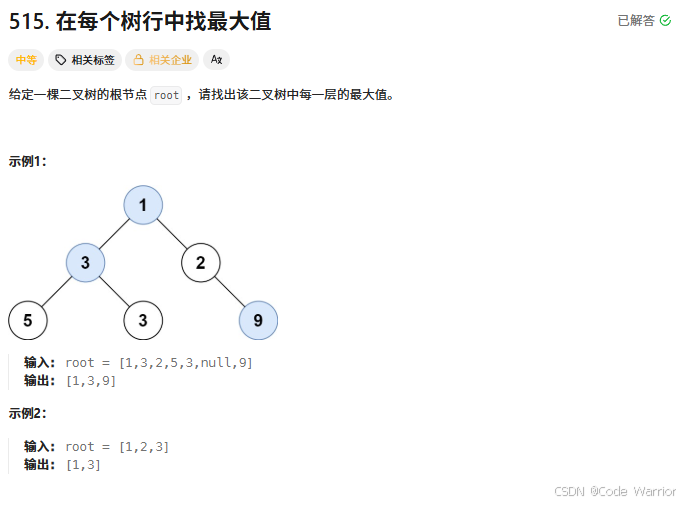
核心思路：二叉樹每層最大值（層序遍歷 + 分組統計）

這段代碼實現了找出二叉樹每一層的最大值，核心思路是利用隊列進行層序遍歷，并在每一層遍歷時維護當前層的最大值。具體步驟如下：

隊列初始化：將根節點加入雙端隊列?q。
循環處理每一層：
- 初始化當前層最大值?ma?為?INT_MIN。
- 鎖定當前層節點數?sz（即隊列當前長度）。
- 遍歷當前層所有節點：
  - 取出隊首節點，更新?ma?為?ma?和當前節點值的較大值。
  - 將該節點的左右子節點（若存在）加入隊列尾部。
  - 從隊列頭部移除當前節點（確保處理完所有當前層節點）。
- 當前層遍歷結束后，將?ma?加入結果數組?ret。
返回結果：遍歷完所有層后，ret?即為每層的最大值數組。

關鍵點

層級控制：通過?sz?鎖定當前層的節點數，確保每次循環處理完一層的所有節點。
最大值維護：在遍歷每層節點時，動態更新當前層的最大值?ma。
隊列操作：
- 入隊：將下一層的節點加入隊列尾部。
- 出隊：從隊列頭部取出并移除當前層的節點。

復雜度分析

時間復雜度：O (n)，每個節點僅入隊 / 出隊一次。
空間復雜度：O (n)，最壞情況下隊列同時存儲一層的所有節點（例如滿二叉樹的最后一層）。

    vector<int> largestValues(TreeNode* root) {vector<int> ret;if(root == nullptr) return ret;deque<TreeNode*> q;q.push_back(root);while(q.size()){int ma = INT_MIN;// deque<TreeNode*> tmp;// for(auto n : q)// {//     ma = max(ma, n->val);//     if(n->left)//         tmp.push_back(n->left);//     if(n->right)//         tmp.push_back(n->right);// }// q = tmp;int sz = q.size();while(sz--){ma = max(ma, (q.front()->val));// TreeNode* t = q.top();// q.pop();if(q.front()->left)q.push_back(q.front()->left);if(q.front()->right)q.push_back(q.front()->right);q.pop_front();}ret.push_back(ma);}return ret;}