摘要

這篇文章帶你用 Swift 實戰一道非常經典的 DFS + 記憶化搜索題目 —— LeetCode 329《矩陣中的最長遞增路徑》。看似一個簡單的“走格子”游戲，實則考察了搜索順序、剪枝策略和狀態緩存等一系列算法技巧。我們將一步步分析這道題的解決過程，并附上可運行的 Swift 代碼及詳細注釋。

描述

給定一個 m x n 整數矩陣 matrix ，找出其中 最長遞增路徑 的長度。

對于每個單元格，你可以往上，下，左，右四個方向移動。 你 不能 在 對角線 方向上移動或移動到 邊界外（即不允許環繞）。

示例 1：

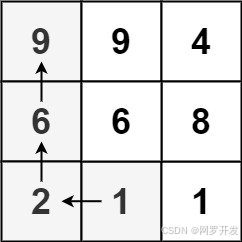
輸入： matrix = [[9,9,4],[6,6,8],[2,1,1]]
輸出： 4 
解釋： 最長遞增路徑為 [1, 2, 6, 9]。

示例 2：

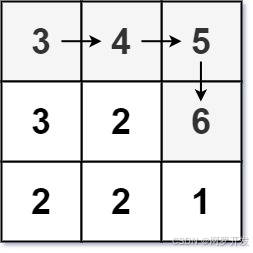
輸入： matrix = [[3,4,5],[3,2,6],[2,2,1]]
輸出： 4 
解釋： 最長遞增路徑是 [3, 4, 5, 6]。注意不允許在對角線方向上移動。

示例 3：

輸入： matrix = [[1]]
輸出： 1

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 231 - 1

題解答案

我們可以用 深度優先搜索（DFS）+ 記憶化搜索（Memoization） 來解決這個問題：

1. 對每個格子 (i, j) 進行 DFS，嘗試向四個方向擴展路徑；
2. 每當發現下一個格子數字更大，就繼續遞歸搜索；
3. 為了避免重復計算，我們使用一個二維數組 cache[i][j] 存儲每個格子的最長路徑長度；
4. 所有格子的 DFS 跑一遍，返回最長的路徑長度即可。

題解代碼分析

import Foundationclass Solution {func longestIncreasingPath(_ matrix: [[Int]]) -> Int {guard !matrix.isEmpty else { return 0 }let m = matrix.countlet n = matrix[0].countvar cache = Array(repeating: Array(repeating: 0, count: n), count: m)let directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]func dfs(_ x: Int, _ y: Int) -> Int {if cache[x][y] != 0 {return cache[x][y]}var maxLength = 1for (dx, dy) in directions {let newX = x + dxlet newY = y + dyif newX >= 0, newX < m, newY >= 0, newY < n,matrix[newX][newY] > matrix[x][y] {maxLength = max(maxLength, dfs(newX, newY) + 1)}}cache[x][y] = maxLengthreturn maxLength}var result = 0for i in 0..<m {for j in 0..<n {result = max(result, dfs(i, j))}}return result}
}

代碼解析

• cache[x][y]：用于記錄格子 (x, y) 的最長路徑長度，避免重復遞歸；
• dfs 是遞歸核心函數，它探索每一個可能的方向；
• directions 列出四個方向（上、下、左、右）；
• 最后遍歷整個矩陣，取所有位置 DFS 的最大值作為結果。

示例測試及結果

我們可以寫一個簡單的測試模塊，驗證這個函數的效果：

let solution = Solution()let matrix1 = [[9, 9, 4],[6, 6, 8],[2, 1, 1]
]
print(solution.longestIncreasingPath(matrix1))  // 輸出: 4let matrix2 = [[3, 4, 5],[3, 2, 6],[2, 2, 1]
]
print(solution.longestIncreasingPath(matrix2))  // 輸出: 4let matrix3 = [[1]
]
print(solution.longestIncreasingPath(matrix3))  // 輸出: 1

運行結果為：

4
4
1

可以看到，函數能準確輸出矩陣中最長遞增路徑的長度。

時間復雜度

• O(m × n)：每個格子只會被訪問一次，因為有緩存機制（記憶化搜索）。
• 對于矩陣中每個格子 (i, j)，我們最多做 4 次方向判斷，但不會重復遞歸。

空間復雜度

• O(m × n)：我們使用了一個 cache 二維數組來保存每個格子的搜索結果；
• 遞歸棧的深度最壞為 m × n，不過大部分情況下都遠小于這個上限。

總結

這道題看起來像暴力 DFS，但只要引入記憶化搜索（Memoization），效率就大幅提升，避免了重復計算。也體現了典型的“搜索+緩存”優化套路。

如果你在刷題中遇到「在圖中找最長路徑」的問題，不妨第一時間考慮：

• 是否可以 DFS 解決？
• 子問題結果能不能緩存？

這個技巧在圖搜索、DP、樹結構中經常用到，是刷題的通關利器。