深度學習入門：了解“閾值激活函數”（Threshold Activation Function）
激活函數是神經網絡中至關重要的一環。今天，我們通過一幅簡單直觀的手繪圖，一起理解最早期也最基礎的激活函數之一 —— 閾值激活函數（Threshold Activation Function）。
1. 前言
在深度學習（Deep Learning）中，激活函數（Activation Function） 決定了神經網絡每個神經元的輸出形式。
沒有激活函數，神經網絡就只是一堆線性疊加，無法擬合復雜的非線性關系。
而在眾多激活函數中，閾值激活函數（Threshold Activation Function） 是最早被提出的一種，它簡單粗暴，卻也奠定了后續復雜模型的基礎。
今天，讓我們從這幅生動的手繪圖出發，深度理解閾值激活的本質。
2. 圖像解讀
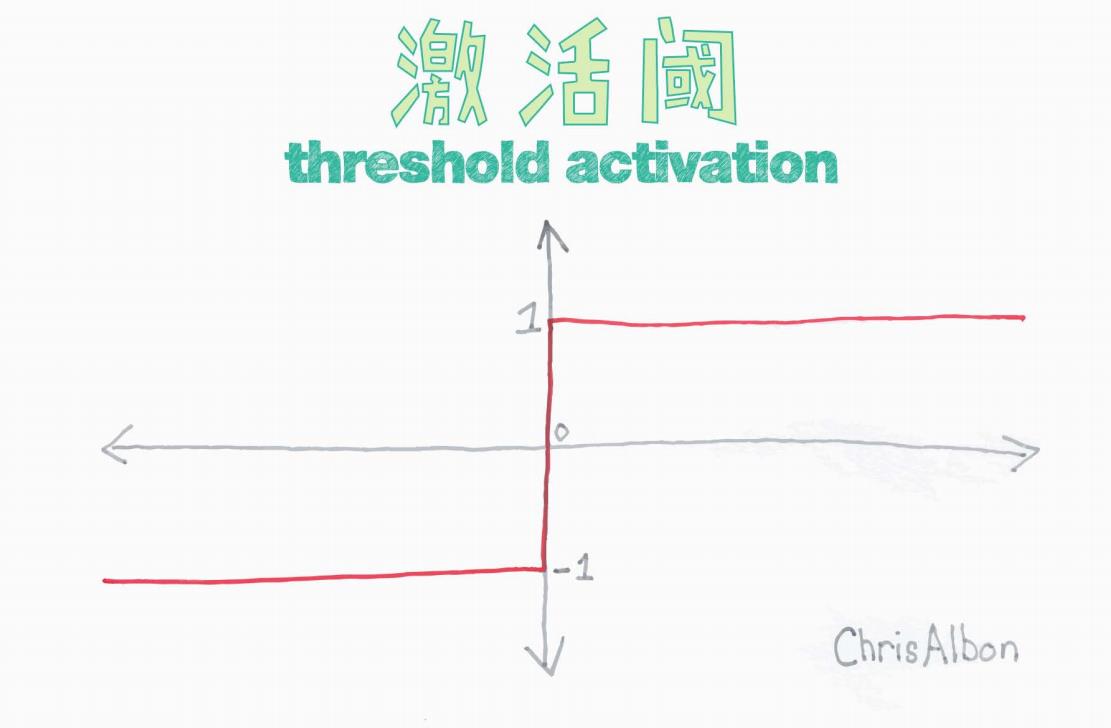
這張圖直觀展示了閾值激活函數的特性：
-
水平方向是輸入（Input），表示神經元接收到的信號。
-
垂直方向是輸出（Output），表示神經元的激活結果。
可以看到：
-
當輸入 > 0 時，輸出固定為 +1。
-
當輸入 < 0 時，輸出固定為 -1。
-
當輸入 = 0 時，通常根據具體定義，輸出可以是 1、-1 或 0，本圖示意以 1 為例。
這種“跳變式”的輸出特性，就是典型的硬閾值（Hard Threshold）行為。
3. 數學表達式
閾值激活函數可以用簡單的公式表示為：
或者在某些變種中：
其中，θ 是一個自定義的閾值（通常為 0）。
4. 背景與起源
-
感知機（Perceptron） —— 1958年，Frank Rosenblatt 提出了世界上第一個神經網絡模型：感知機。
-
在感知機中，激活函數就是一個簡單的閾值函數：加權求和后，大于某個閾值就激活為1，否則激活為-1。
-
這種方式使得神經網絡能夠完成最簡單的分類任務（如二分類問題）。
可以說，閾值激活函數是神經網絡史上的第一代激活函數。
5. 特點與優缺點
優點
-
實現簡單：僅需判斷大小關系。
-
計算快速：適合硬件直接實現。
-
清晰明了：特別適合線性可分問題（如簡單分類）。
缺點
-
不可導：函數在 x=0 處不可導，無法直接用于反向傳播（Backpropagation）訓練。
-
不連續：輸出突然跳變，不利于梯度更新。
-
信息量少：只有兩個輸出（+1 或 -1），表達能力有限。
這些缺點直接促成了后續更復雜激活函數（如 Sigmoid、ReLU、Tanh 等）的發展。
6. 應用場景
雖然在現代深度學習中，硬閾值激活已經很少直接使用，但它仍然在一些場景下非常有用：
-
早期神經網絡（如感知機）教學與演示。
-
硬件實現（如 FPGA、低功耗芯片），需要簡單快速的決策邏輯。
-
二分類任務中，粗略建模或快速實驗。
-
神經形態計算（Neuromorphic Computing），模擬生物神經元開關行為。
此外，它作為一種概念模型，幫助人們直觀理解激活函數的意義 —— 將連續的輸入信號轉化為離散的決策輸出。
7. 與現代激活函數的對比
| 特性 | 閾值激活（Threshold） | Sigmoid | ReLU |
|---|---|---|---|
| 是否可導 | 否 | 是 | 部分可導 |
| 是否連續 | 否 | 是 | 是 |
| 輸出范圍 | {?1,1} 或 {0,1} | (0,1) | [0,+∞) |
| 是否易于訓練 | 否 | 是 | 是 |
| 典型應用 | 感知機、簡單分類 | 早期神經網絡 | 現代深度學習 |
可以看到，隨著神經網絡規模擴大和應用復雜化，更平滑、可導的激活函數成為主流。
8. 總結
雖然閾值激活函數簡單、粗糙，但它是神經網絡發展的起點。
它讓我們明白了一個基本概念：
神經網絡不僅要加權輸入，更需要通過非線性函數進行處理，才能模擬復雜的決策與認知過程。
了解它，就像了解一棵參天大樹的根 —— 簡單，卻無比重要。
9. 參考資料
-
Rosenblatt, F. (1958). The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain.
-
Ian Goodfellow, Yoshua Bengio, Aaron Courville. (2016). Deep Learning.
-
Chris Albon - Machine Learning Flashcards
尾聲
如果你喜歡今天這篇文章，歡迎點贊、收藏、評論支持！
?
個人效率)
