牛客對應題目鏈接：字符串的排列_牛客題霸_牛客網 (nowcoder.com)

力扣對應題目鏈接：LCR 157. 套餐內商品的排列順序 - 力扣（LeetCode）

核心考點 ：全排列問題， DFS。

---

一、《劍指Offer》對應內容

---

二、分析題目

全排列問題，可以看做如下多叉樹形態：

---

三、代碼

//牛客
//寫法一
class Solution {
private:set<string> ans;vector<string> res;
public:/*** 代碼中的類名、方法名、參數名已經指定，請勿修改，直接返回方法規定的值即可** * @param str string字符串 * @return string字符串vector*/void swap(string &str, int i, int j){char temp=str[i];str[i]=str[j];str[j]=temp;}void dfs(string &str, int start){if(start==str.length()-1){ans.insert(str);return;}for(int i=start; i<str.size(); i++){swap(str, start, i);dfs(str, start+1);swap(str, start, i);}}vector<string> Permutation(string str) {int n=str.size();if(n<1) return {""};dfs(str, 0);for(auto s : ans)res.push_back(s);return res;}
};//寫法二
class Solution {
private:set<string> ans;
public:/*** 代碼中的類名、方法名、參數名已經指定，請勿修改，直接返回方法規定的值即可** * @param str string字符串 * @return string字符串vector*/void dfs(string &str, int pos){if(pos==str.length()-1){ans.insert(str);return;}for(int i=pos; i<str.size(); i++){swap(str[pos], str[i]);dfs(str, pos+1);swap(str[pos], str[i]);}}vector<string> Permutation(string str) {if(str.size()<1) return {""};dfs(str, 0);return vector<string>({ans.begin(), ans.end()});}
};//力扣
class Solution {
private:set<string> ans;vector<string> res;
public:void dfs(string& goods, int pos){if(pos==goods.size()-1){ans.insert(goods);return;}for(int i=pos; i<goods.size(); i++){swap(goods[pos], goods[i]);dfs(goods, pos+1);swap(goods[pos], goods[i]);}}vector<string> goodsOrder(string goods) {dfs(goods, 0);for(auto s : ans)res.push_back(s);return res;}
};

---

四、擴展

---

五、相關題目

1、正方體的三面和

輸入一個含有 8 個數字的數組，判斷有沒有可能把這 8 個數字分別放到正方體的 8 個頂點上（如圖 4.15 所示），使得正方體上三組相對的面上的 4 個頂點的和都相等。

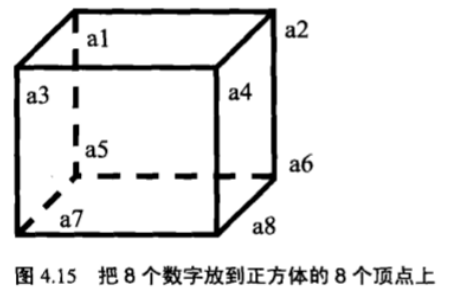
這相當于先得到 a1、a2、a3、a4、a5、a6、a7 和 a8 這 8 個數字的所有排列，然后判斷有沒有某一個的排列符合題目給定的條件，即 a1+a2+a3+a4==a5+a6+a7+a8，a1+a3+a5+a7==a2+a4+a6+a8，并且 a1+a2+a5+a6==a3+a4+a7+a8。

---

2、八皇后

在 8 X 8 的國際象棋上擺放 8 個皇后，使其不能相互攻擊，即任意兩個皇后不得處在同一行、同一列或者同一對角線上。圖 4.16 中的每個黑色格子表示一個皇后，這就是一種符合條件的擺放方法。請問總共有多少種符合條件的擺法？

由于 8 個皇后的任意兩個不能處在同一行，那么肯定是每一個皇后占據一行。于是我們可以定義一個數組 ColumnIndex[8]，數組中第 i 個數字表示位于第 i 行的皇后的列號。先把 ColumnIndex 的 8 個數字分別用 0~7 初始化，接下來就是對數組 ColumnIndex 做全排列。因為我們是不同的數字初始化數組，所以任意兩個皇后肯定不同列。我們只需判斷每一個排列對應的 8 個皇后是不是在同意對角線上，也就是對于數組的兩個下標 i 和 j，是不是 i-j==ColumnIndex[i]-ColumnIndex[j] 或者 j-i==ColumnIndex[i]-ColumnIndex[j]。

---

力扣對應類似題目鏈接：51. N 皇后 - 力扣（LeetCode）

//寫法一
class Solution {
private:vector<string> path;vector<vector<string>> res;vector<bool> checkCol, checkDg, checkUdg;
public:void dfs(int row, int n){if(row==n){res.push_back(path);return;}for(int col=0; col<n; col++){if (!checkCol[col] && !checkDg[row-col+n] && !checkUdg[row+col]){path[row][col]='Q';checkCol[col]=checkDg[row-col+n]=checkUdg[row+col]=true;dfs(row+1, n);checkCol[col]=checkDg[row-col+n]=checkUdg[row+col]=false;path[row][col]='.';}}}vector<vector<string>> solveNQueens(int n) {checkCol = vector<bool>(n, false);checkDg = vector<bool>(2*n, false);checkUdg = vector<bool>(2*n, false);path.resize(n);for(int i=0; i<n; i++)path[i].append(n, '.');dfs(0, n);return res;}
};//寫法二
class Solution {
public:vector<vector<string>> res;void dfs(int x, int n, vector<string>& chessboard){if(x==n){res.push_back(chessboard);return;}for (int y=0; y<n; y++){if (isValid(x, y, n, chessboard)){chessboard[x][y]='Q';dfs(x+1, n, chessboard);chessboard[x][y]='.';}}}bool isValid(int x, int y, int n, vector<string>& chessboard){// 檢查列for (int i=0; i<x; i++){if (chessboard[i][y]=='Q')return false;}// 檢查 45度角是否有皇后for (int i=x-1, j=y-1; i>=0 && j>=0; i--, j--){if (chessboard[i][j]=='Q')return false;}// 檢查 135度角是否有皇后for(int i=x-1, j=y+1; i>=0 && j<n; i--, j++){if (chessboard[i][j]=='Q')return false;}return true;}vector<vector<string>> solveNQueens(int n) {vector<string> chessboard(n, string(n, '.'));dfs(0, n, chessboard);return res;}
};

---

六、舉一反三

如果面試題是按照一定要求擺放若干個數字，我們可以先求出這些數字的所有排列，然后再一一判斷每個排列是不是滿足題目給定的要求。