數學上稱無限次可導函數是光滑的或沒有奇異性,若函數在某處有間斷或某階導數不連續,則稱函數在此處有奇異性,該點就是奇異點。奇異性反映了信號的不規則程度,因為信號的奇異點和突變部分往往攜帶者重要信息,因此信號的奇異性檢測非常有必要。信號的奇異性由Lipschitz指數來描述和衡量。
通常情況下,信號的奇異性可分為兩種情況:一種是信號在某一時刻,其幅值發生突變,引起信號的不連續性,另一種是信號外觀上光滑,其幅值沒有突變,但是在信號的一階微分上有突變產生。Fourier變換是研究函數奇異性的基本工具,但它只能確定信號是否具有奇異性和奇異性的強弱,而不能確定奇異點的分布情況及奇異點的位置。由于小波變換理論在時域和頻域良好的局部化或近似局部化性質,因此小波變換作為檢測信號奇異性的工具,較好地解決了信號奇異檢測的問題。
當小波函數可看做某一平滑函數的一階導數時,信號小波變換模的局部極值點對應于信號的突變點(或邊緣),因此,采用檢測小波變換系數模的過零點和局部極值點的方法可以檢測信號的突變點。
鑒于此,采用小波模極大值分解與重建對一維時間序列信號進行處理,運行環境為matlab R2018A,主運行代碼如下:
%% 小波模極大值重構是采用的交替投影法
close all;
points = 1024; % 所處理數據的長度
level = 6; % 分解的級數
sr = 360; % 抽樣率, P gama投影要用的
num_inter = 6; % 迭代次數
wf='db3'; % 小波名稱
[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters(wf);% 得到小波變換要用的濾波器
%ecgdata = load('ecg.txt'); %需要分析的信號
%signal = ecgdata(1:points,3)';% 取第3列,不懂可以打開ecg.txt看一下% 這個信號是可以換的,做過一個信號文件就可以。
%signal = signal * 300; % 乘以300,數據大一點顯示出來漂亮一點,不為什么
%調用wave_peak進行小波變換,計算小波分解系數和模極大序列
signal = signal_fig1;
[swa,swd,ddw,wpeak] = wave_peak(signal,level,Lo_D,Hi_D);
% signal: 原始信號; swa:小波概貌; swd:小波細節;
% ddw: 局部極大位置; wpeak:小波變換的局部極大序列]
% 作圖:左列為各層的概略信號,右列為各層的細節信號(即小波變換)
figure;
subplot(level,1,1); plot(real(signal)); grid on;axis tight;
title('original signal(Upper)、wavelet transform (Lower left)and modulus maxima(Lower right)');
for i=1:level%概略信號subplot(level+1,3,3*(i)+1);plot(swa(i,:)); axis tight; grid on; xlabel('time');ylabel(strcat('a ',num2str(i)));%小波變換subplot(level+1,3,3*(i)+2);plot(swd(i,:)); axis tight;grid on;ylabel(strcat('d ',num2str(i)));%模極大值subplot(level+1,3,3*(i)+3);plot(wpeak(i,:)); axis tight;grid on;ylabel(strcat('j= ',num2str(i)));
endpswa = swa(level,:); % pswa: 第level層的概略信號仍然保留為重構用
wframe = (wpeak~=0); % wframe 中的1標明wpeak非零的位置,即模極大值的位置
%迭代初始化
w0=zeros(1,points); % 重構信號初始值設為0
[a,d]=swt(w0,level,Lo_D,Hi_D); % 做一次穩定小波變換,結果在a和d里面,層數level不變
w2=d; % w2為待重建小波,上一行和這一行好像可以省去for j=1:num_inter % 循環重構,d -> w2 -> w0 -> d -> w2 -> w0 -> dw2=Py_Pgama(d,wpeak,wframe,1,sr); % 先進行Py投影和 Pgama投影w0=iswt(pswa,w2,Lo_R,Hi_R); % 再進行Pv投影(小波逆變換)[a,d]=swt(w0,level,Lo_D,Hi_D); % Pvend
% 最后通過w2做逆小波變換得到重構信號:
pswa = iswt(swa(level,:),w2,Lo_R,Hi_R); % 計算重建信號% 原信號和由模極大重建信號的比較
figure,
subplot(211);
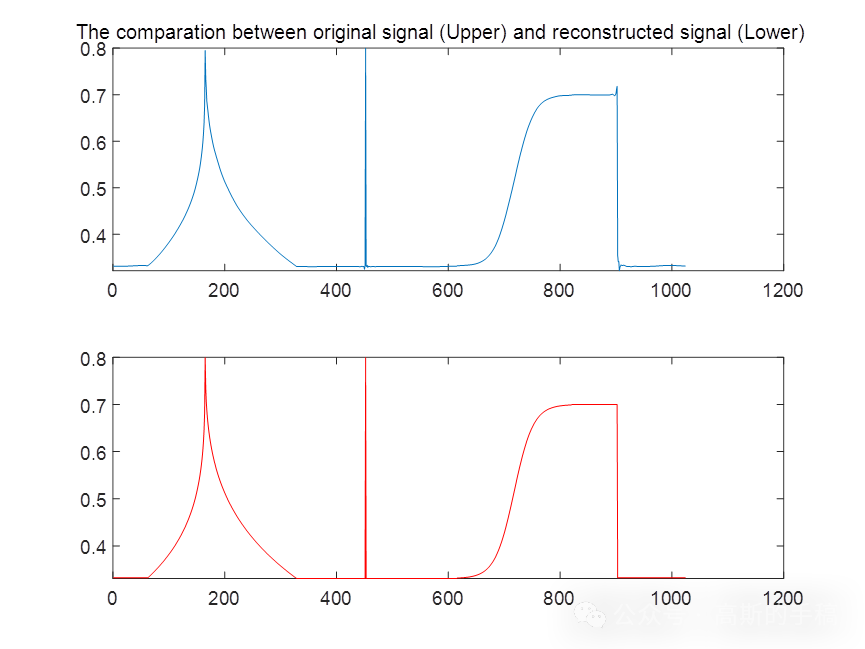
plot(pswa(1:points)); % 重構信號描圖
title('The comparation between original signal (Upper) and reconstructed signal (Lower)');
subplot(212);
plot(signal(1:points),'r'); % 原始信號描圖%分別計算重建小波以及原信號的信噪比
werr = w2 - swd; % 原信號的小波變換的細節部分和重構信號的細節部分的誤差,即
% 原信號的小波變換(swd)和重建后的小波變換(w2)的比較
figure,
wsnr = zeros(level,1); % 存儲每一層的信噪比
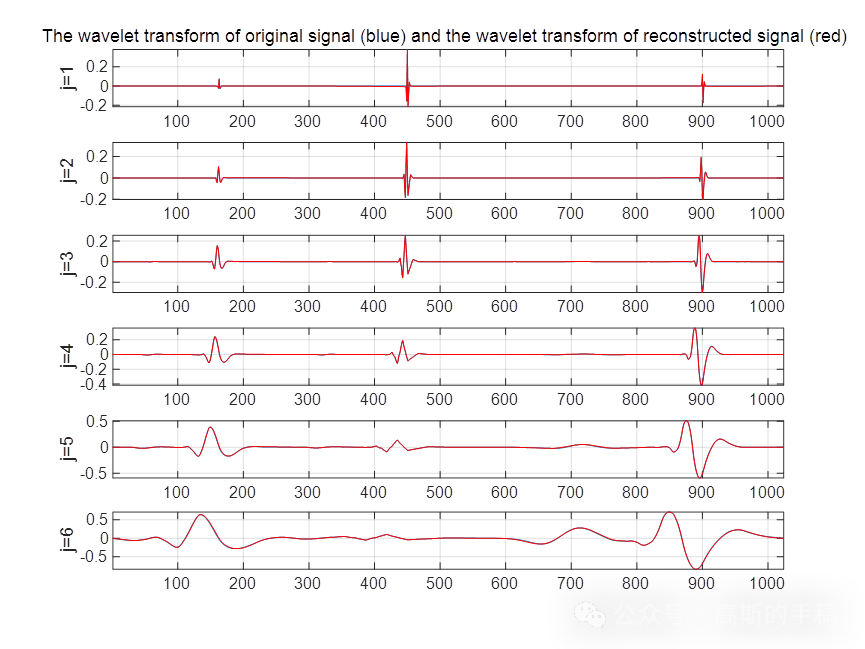
for m=1:level % norm為2范數,即均方值wsnr(m) = 20*log10(norm(swd(m,:))/norm(werr(m,:)));subplot(level,1,m);plot(swd(m,:)),hold on,%紅色的重構小波變換覆蓋在原圖上plot(w2(m,:),'r');grid on;ylabel(strcat('j=',num2str(m))),axis tight;if(m==1)title('The wavelet transform of original signal (blue) and the wavelet transform of reconstructed signal (red)');end
endwsnr % 小波域計算出的各層的信噪比
err = pswa(1:points)-signal(1:points); % 時域的誤差信號
mse = mean(err.^2) % 均方誤差
smse = mean(signal.^2); % 信號的均方值
%完整代碼:https://mbd.pub/o/bread/mbd-ZZeTmZ5u
snr = 10*log10(smse/mse) % 時域中計算的信噪比(dB值)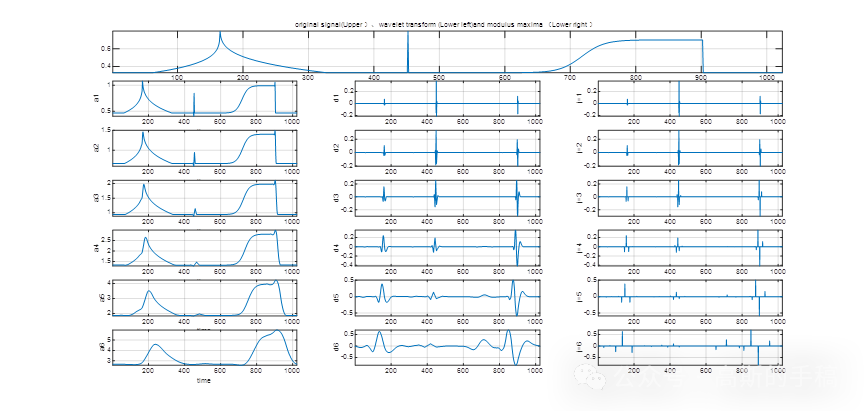
工學博士,擔任《Mechanical System and Signal Processing》《中國電機工程學報》《控制與決策》等期刊審稿專家,擅長領域:現代信號處理,機器學習,深度學習,數字孿生,時間序列分析,設備缺陷檢測、設備異常檢測、設備智能故障診斷與健康管理PHM等。







筆記)
)





)
)



