【基本數據結構】平衡二叉樹

文章目錄

  • 前言
  • 平衡二叉樹
    • 1 簡介
    • 2 旋轉
      • 2.1 左旋
      • 2.2 右旋
      • 2.3 何時旋轉
    • 3 插入節點
    • 4 刪除節點
    • 5 代碼
  • 參考資料
  • 寫在最后

前言

本系列專注更新基本數據結構，現有以下文章：

【算法與數據結構】數組.

【算法與數據結構】鏈表.

【算法與數據結構】哈希表.

【算法與數據結構】二叉查找樹

【算法與數據結構】平衡二叉樹

平衡二叉樹

1 簡介

平衡二叉樹是為了解決二叉查找樹中樹退化成鏈這一問題而提出的。平衡二叉樹在插入、刪除某一節點之后通過左旋或右旋操作保持動態平衡，從而避免節點失衡（最壞的情況是樹退化成鏈）。

二叉樹某節點是否失衡由該節點的 失衡因子 來衡量，失衡因子為左子樹節點高度與右子節點高度之差。

當二叉樹中某節點的左、右子樹高度差不超過1，則表示該節點平衡，高度差不超過 1 對應平衡因子的值為 ±1 和 0。

左旋與右旋，由于插入、刪除節點導致二叉樹中出現不平衡節點，此時可以通過左旋或右旋操作調整節點位置以達到二叉查找樹的動態平衡。平衡二叉樹也是一棵二叉查找樹，它的查找、插入、刪除都與二叉查找樹的操作相同，只是在插入、刪除新的節點之后需要通過一些旋轉操作來保持其平衡性。

2 旋轉

2.1 左旋

左旋，顧名思義，指的是向左旋轉節點，或者是逆時針旋轉節點。在圖 2-1 中，由于插入了一個新的節點到平衡二叉樹中，根節點 3 平衡因子變為 0-2=-2，說明此時根節點已經失衡了。為了保持這棵二叉查找樹的平衡性，需要左旋根節點。

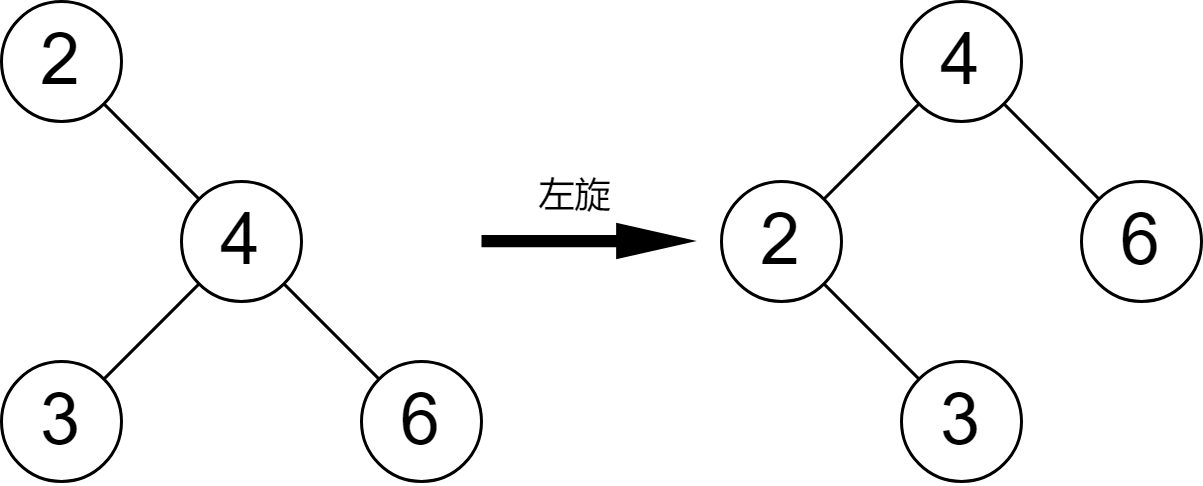
平衡二叉樹-左旋.drawio (1)
圖 2-1 左旋

實現代碼

// 左旋操作
Node* leftRotate(Node* x) {Node* y = x->right;Node* T2 = y->left;y->left = x;x->right = T2;x->height = std::max(height(x->left), height(x->right)) + 1;y->height = std::max(height(y->left), height(y->right)) + 1;return y;
}

上述代碼是左旋的具體操作，傳入的一個節點指針 x，表示從該節點開始進行左旋，最終返回的是左旋操作后該子樹新的根節點。

以圖 2-1 為例，傳入的節點為 3，首先記錄 3 的右子節點 4，記作 y；接著記錄 y 的左子節點空節點，記作 T2；接下來將 4 的左鏈接連到 3 上，3 的右鏈接連到空節點上。

最后，還需要更新節點 x 和 y 的高度，為后面計算平衡因子做準備。

2.2 右旋

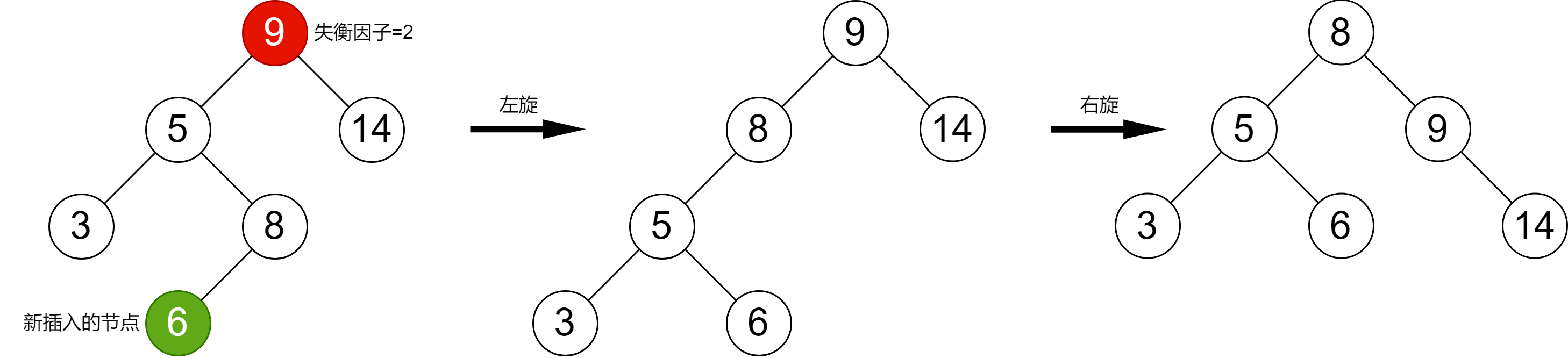
右旋，指的是向右旋轉節點，或者是順時針旋轉節點。在圖 2-2 中，由于插入了一個新的節點到平衡二叉樹中，根節點 9 平衡因子變為 2-0=2，說明此時根節點已經失衡了。為了保持這棵二叉查找樹的平衡性，需要右旋根節點。

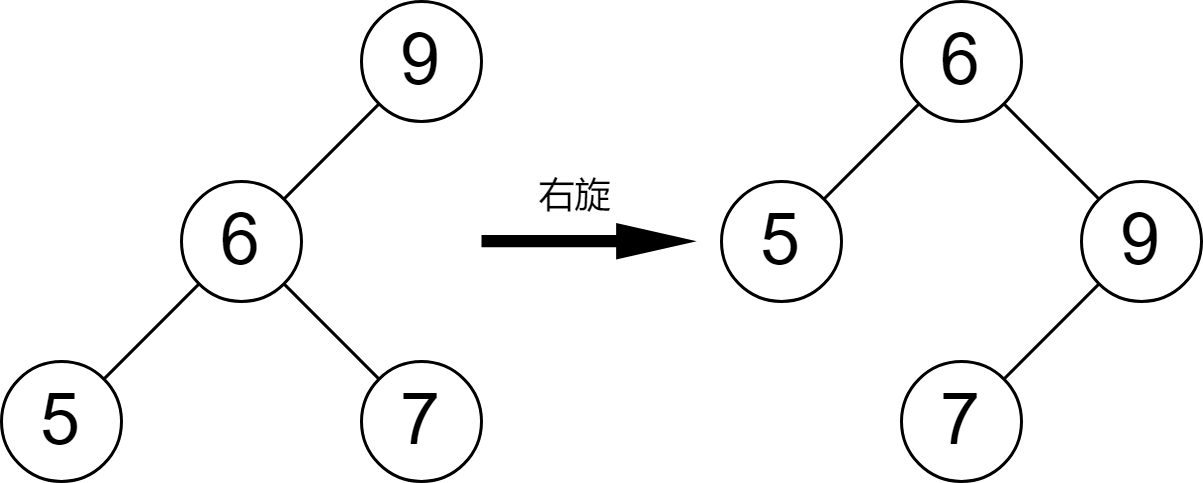
平衡二叉樹-右旋.drawio (1)
圖 2-2 右旋

實現代碼

// 右旋操作
Node* rightRotate(Node* y) {Node* x = y->left;Node* T2 = x->right;x->right = y;y->left = T2;y->height = std::max(height(y->left), height(y->right)) + 1;x->height = std::max(height(x->left), height(x->right)) + 1;return x;
}

右旋操作與左旋操作類似，具體實現見代碼。

2.3 何時旋轉

什么時候需要進行旋轉操作，當然是失衡的時候。以下列出的是失衡的四種情況，以及為了保持平衡需要做出的旋轉決策：

  • LL型，在當前節點的左子節點的左子節點插入新的節點后，當前節點失衡，此時為了保持平衡需要右旋當前節點。
  • RR型，在當前節點的右子節點的右子節點插入新的節點后，當前節點失衡，此時為了保持平衡需要左旋當前節點。
  • LR型，在當前節點的左子節點的右子節點插入新的節點后，當前節點失衡，此時為了保持平衡需要先左旋當前節點的左子節點，再右旋當前節點。
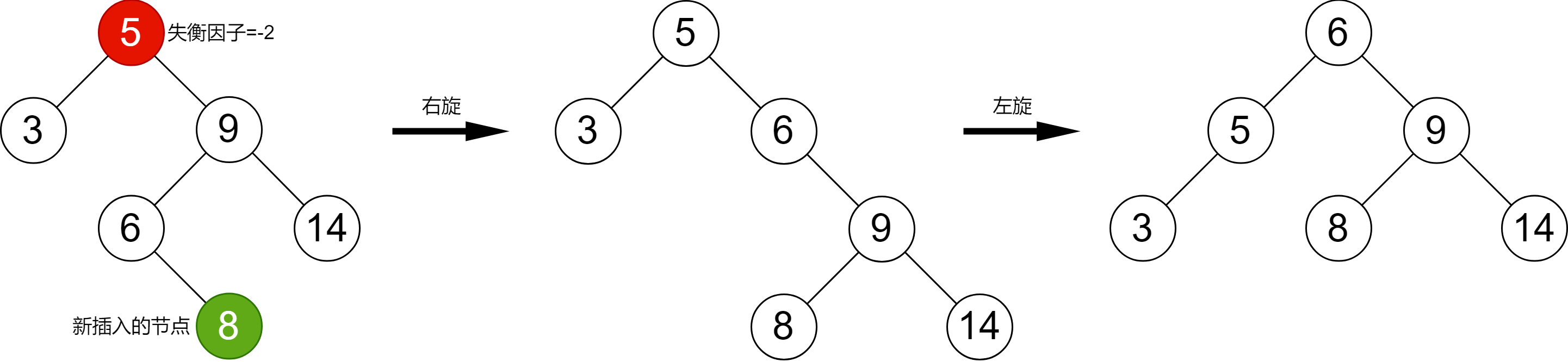
  • RL型，在當前節點的右子節點的左子節點插入新的節點后，當前節點失衡，此時為了保持平衡需要先右旋當前節點的右子節點，再左旋當前節點。

在 LL型 情況中，我們注意到失衡節點的失衡因子為 2，失衡節點的左子節點的失衡因子為 1。類似的，在 RR型 中，失衡節點的失衡因子為 -2，失衡節點的失衡因子為 -1；在 LR型 中，失衡節點的失衡因子為 2，失衡節點的失衡因子為 -1；在 RL型 中，失衡節點的失衡因子為 -2，失衡節點的失衡因子為 1。于是，我們可以根據失衡節點的失衡因子、失衡節點的左子節點的失衡因子、失衡節點的右子節點的失衡因子來判斷當前是什么類型，進而做出相應的旋轉決策。

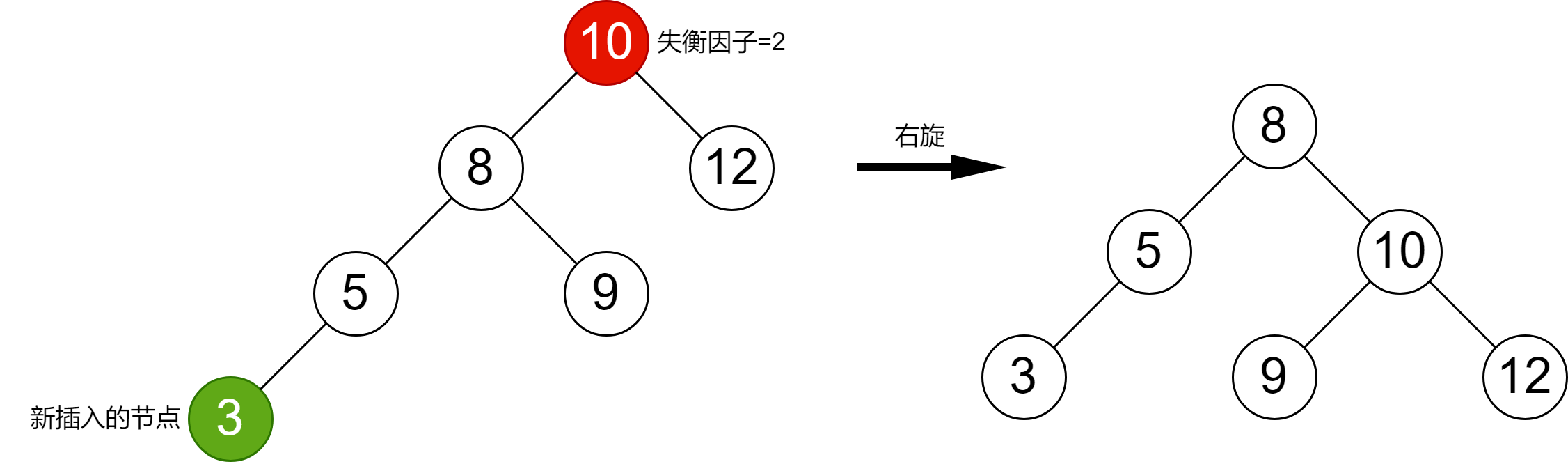
平衡二叉樹-LL型.drawio
圖 2-3 LL型
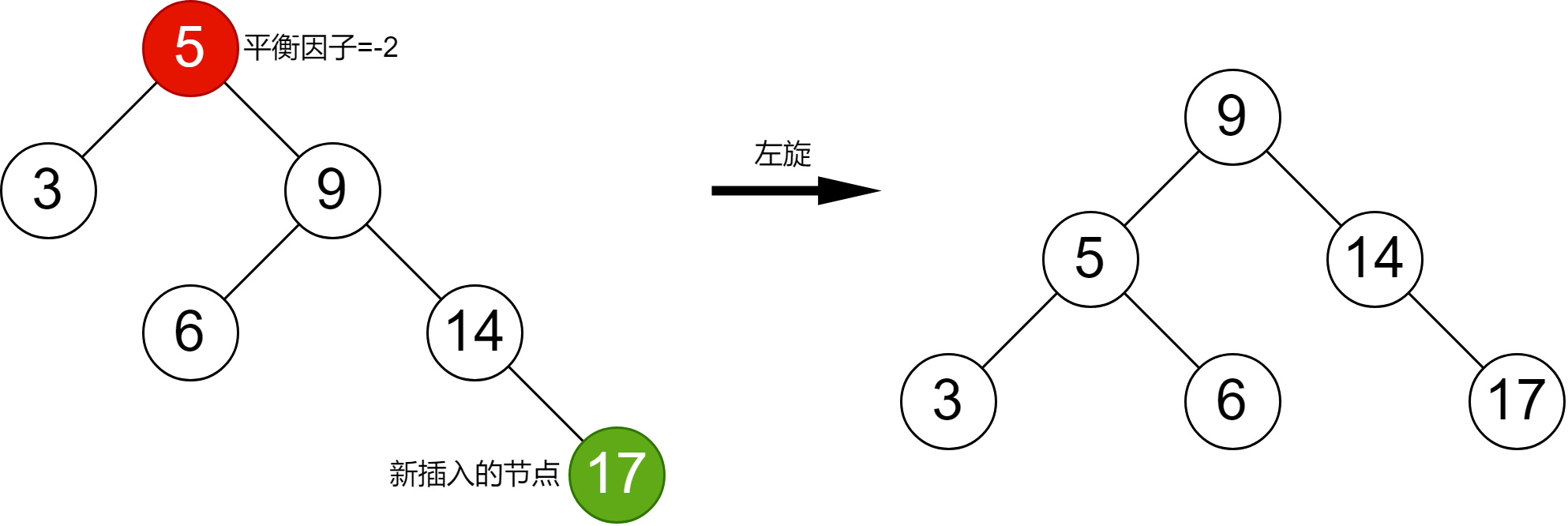
平衡二叉樹-RR型.drawio
圖 2-4 RR型
平衡二叉樹-LR型.drawio
圖 2-5 LR型
平衡二叉樹-RL型.drawio
圖 2-6 RL型

3 插入節點

插入節點和在二叉查找樹中插入節點一樣，先進行未命中的查找，將節點插入到合適的位置。然后根據以上四種情況進行旋轉以保持平衡二叉樹的平衡性。比如在圖 2-6 中插入一個新的節點 8，通過二分查找確定節點 8 的位置為節點 6 右子節點。但是插入節點 8 之后，造成根節點 5 的平衡因子失衡了。因為這是 RL型 情況，所以先右旋根節點的右子樹，然后再左旋根節點。

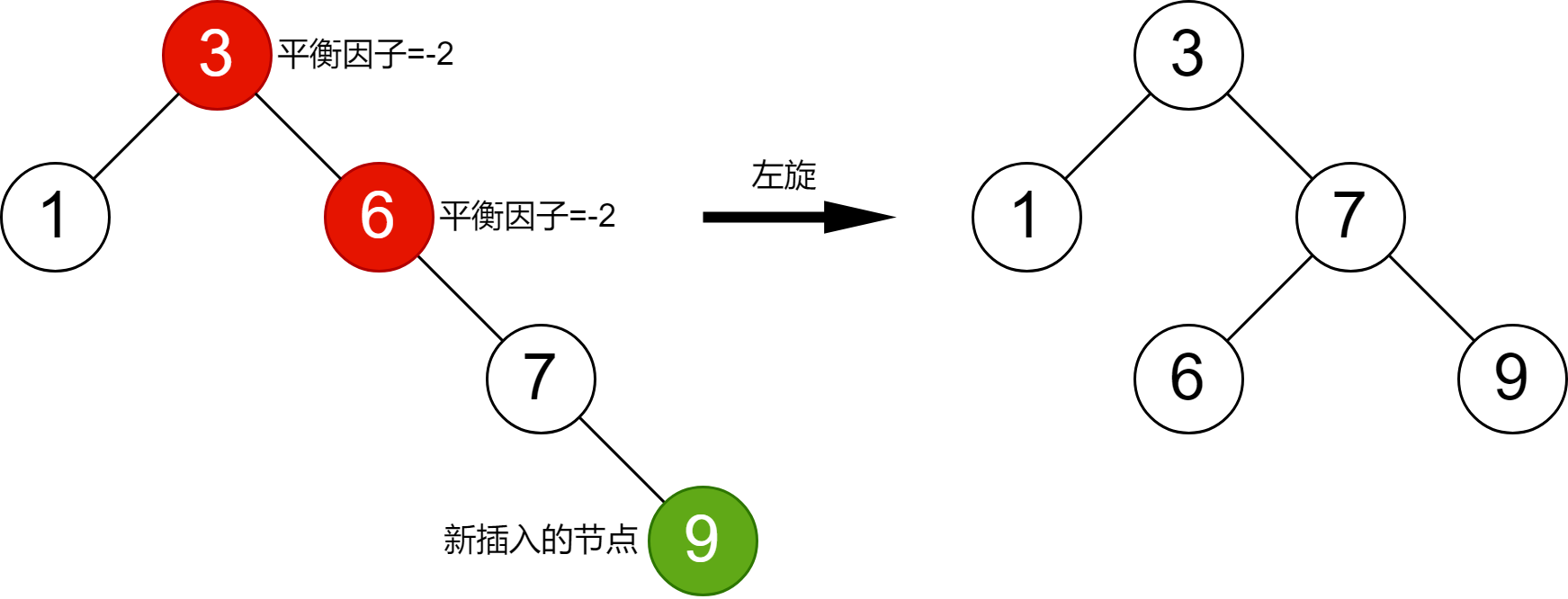
需要注意的是，當插入節點導致多個祖先節點失衡，只需要調整距離插入節點最近的失衡節點即可，其他失衡節點會自動平衡。

平衡二叉樹-插入-注意事項.drawio (1)
圖 3-1 調整最近的失衡節點

實現代碼

// 插入節點
Node* insert(Node* node, int key) {if (node == nullptr)return new Node(key);if (key < node->key)node->left = insert(node->left, key);else if (key > node->key)node->right = insert(node->right, key);elsereturn node;node->height = 1 + std::max(height(node->left), height(node->right));int balance = getBalance(node);// LL 型if (balance > 1 && key < node->left->key)return rightRotate(node);// RR 型if (balance < -1 && key > node->right->key)return leftRotate(node);// LR 型if (balance > 1 && key > node->left->key) {node->left = leftRotate(node->left);return rightRotate(node);}// RL 型if (balance < -1 && key < node->right->key) {node->right = rightRotate(node->right);return leftRotate(node);}return node;
}

在上述插入代碼中，我們先進行未命中的查找，在遞歸查找中插入新的節點。接著，更新當前根節點的高度。最后根據當前節點的平衡因子的不同值來確定是哪一個類型，再根據不同的類型進行相應的調整。具體地：

  • 如果當前節點的失衡因子為 2，并且是在當前節點的左子節點的左子節點插入新的節點，則是 LL 型，右旋該節點即可；
  • 如果當前節點的失衡因子為 -2，并且是在當前節點的右子節點的右子節點插入新的節點，則是 RR 型，左旋節點即可；
  • 如果當前節點的失衡因子為 2，并且是在當前節點的左子節點的右子節點插入新的節點，則是 LR 型，先左旋該節點的左子節點，再右旋該節點；
  • 如果當前節點的失衡因子為 -2，并且是在當前節點的右子節點的左子節點插入新的節點，則是 RL 型，先右旋該節點的右子節點，再左旋該節點；

4 刪除節點

刪除節點操作也需要先進行查找，遞歸的進行查找。查找到需要刪除的節點 root 之后，按照以下情況進行處理：

  • 如果該節點是葉子節點，直接刪除該節點；
  • 如果該節點僅有左子節點或者右子節點，則刪除對應的子節點；
  • 如果該節點的左右節點都齊全，則用右子節點中最小的節點更新 root，并刪除這個右子節點。

接著更新 root 的高度。最后將失衡的節點旋轉，保持平衡。依然是根據當前節點與左、右子節點的平衡因子來判斷屬于哪種旋轉情況，然后進行相應的旋轉。

實現代碼

// 刪除節點
Node* deleteNode(Node* root, int key) {if (root == nullptr)return root;if (key < root->key)root->left = deleteNode(root->left, key);else if (key > root->key)root->right = deleteNode(root->right, key);else {if ((root->left == nullptr) || (root->right == nullptr)) {Node* temp = root->left ? root->left : root->right;if (temp == nullptr) {temp = root;root = nullptr;} else*root = *temp;delete temp;} else {Node* temp = minValueNode(root->right);root->key = temp->key;root->right = deleteNode(root->right, temp->key);}}if (root == nullptr)return root;root->height = 1 + std::max(height(root->left), height(root->right));int balance = getBalance(root);if (balance > 1 && getBalance(root->left) >= 0)return rightRotate(root);if (balance > 1 && getBalance(root->left) < 0) {root->left = leftRotate(root->left);return rightRotate(root);}if (balance < -1 && getBalance(root->right) <= 0)return leftRotate(root);if (balance < -1 && getBalance(root->right) > 0) {root->right = rightRotate(root->right);return leftRotate(root);}return root;
}

5 代碼

#include <iostream>
#include <algorithm>class AVLTree {
private:struct Node {int key;Node* left;Node* right;int height;Node(int k) : key(k), left(nullptr), right(nullptr), height(1) {}};Node* root;int height(Node* n) {return n == nullptr ? 0 : n->height;}// 求平衡因子int getBalance(Node* n) {return n == nullptr ? 0 : height(n->left) - height(n->right);}// 右旋操作Node* rightRotate(Node* y) {Node* x = y->left;Node* T2 = x->right;x->right = y;y->left = T2;y->height = std::max(height(y->left), height(y->right)) + 1;x->height = std::max(height(x->left), height(x->right)) + 1;return x;}// 左旋操作Node* leftRotate(Node* x) {Node* y = x->right;Node* T2 = y->left;y->left = x;x->right = T2;x->height = std::max(height(x->left), height(x->right)) + 1;y->height = std::max(height(y->left), height(y->right)) + 1;return y;}// 插入節點Node* insert(Node* node, int key) {if (node == nullptr)return new Node(key);if (key < node->key)node->left = insert(node->left, key);else if (key > node->key)node->right = insert(node->right, key);elsereturn node;node->height = 1 + std::max(height(node->left), height(node->right));int balance = getBalance(node);// LL 型if (balance > 1 && key < node->left->key)return rightRotate(node);// RR 型if (balance < -1 && key > node->right->key)return leftRotate(node);// LR 型if (balance > 1 && key > node->left->key) {node->left = leftRotate(node->left);return rightRotate(node);}// RL 型if (balance < -1 && key < node->right->key) {node->right = rightRotate(node->right);return leftRotate(node);}return node;}// 獲得最小節點值Node* minValueNode(Node* node) {Node* current = node;while (current->left != nullptr)current = current->left;return current;}// 刪除節點Node* deleteNode(Node* root, int key) {if (root == nullptr)return root;if (key < root->key)root->left = deleteNode(root->left, key);else if (key > root->key)root->right = deleteNode(root->right, key);else {if ((root->left == nullptr) || (root->right == nullptr)) {Node* temp = root->left ? root->left : root->right;if (temp == nullptr) {temp = root;root = nullptr;} else*root = *temp;delete temp;} else {Node* temp = minValueNode(root->right);root->key = temp->key;root->right = deleteNode(root->right, temp->key);}}if (root == nullptr)return root;root->height = 1 + std::max(height(root->left), height(root->right));int balance = getBalance(root);if (balance > 1 && getBalance(root->left) >= 0)return rightRotate(root);if (balance > 1 && getBalance(root->left) < 0) {root->left = leftRotate(root->left);return rightRotate(root);}if (balance < -1 && getBalance(root->right) <= 0)return leftRotate(root);if (balance < -1 && getBalance(root->right) > 0) {root->right = rightRotate(root->right);return leftRotate(root);}return root;}// 查找節點Node* search(Node* root, int key) {if (root == nullptr || root->key == key)return root;if (key < root->key)return search(root->left, key);return search(root->right, key);}// 中序遍歷void inOrder(Node* root) {if (root != nullptr) {inOrder(root->left);std::cout << root->key << " ";inOrder(root->right);}}public:AVLTree() : root(nullptr) {}// 插入節點的對外接口void insert(int key) {root = insert(root, key);}// 刪除節點的對外接口void deleteNode(int key) {root = deleteNode(root, key);}// 搜索節點的對外接口bool search(int key) {return search(root, key) != nullptr;}// 中序遍歷的對外接口void inOrder() {inOrder(root);std::cout << std::endl;}
};int main() {AVLTree tree;tree.insert(10);tree.insert(20);tree.insert(30);tree.insert(40);tree.insert(50);tree.insert(25);std::cout << "中序遍歷后的AVL樹: ";tree.inOrder();tree.deleteNode(10);std::cout << "刪除節點10后的AVL樹: ";tree.inOrder();int key = 25;if (tree.search(key))std::cout << "找到節點: " << key << std::endl;elsestd::cout << "未找到節點: " << key << std::endl;return 0;
}

參考資料

【視頻】平衡二叉樹(AVL樹)

寫在最后

如果您發現文章有任何錯誤或者對文章有任何疑問，歡迎私信博主或者在評論區指出 💬💬💬。

如果大家覺得有些地方需要補充，歡迎評論區交流。

最后，感謝您的閱讀，如果有所收獲的話可以給我點一個 👍 哦。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/bicheng/20590.shtml
繁體地址，請注明出處：http://hk.pswp.cn/bicheng/20590.shtml
英文地址，請注明出處：http://en.pswp.cn/bicheng/20590.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

【斯坦福因果推斷課程全集】1_隨機對照試驗1

【斯坦福因果推斷課程全集】1_隨機對照試驗1

目錄 The average treatment effect Difference-in-means estimation IID Sampling and Population Asymptotics Example: The linear model Regression adjustments with a linear model 隨機對照試驗&#xff08;RCT&#xff09;是統計因果推論的基礎。如果有的話&#…
閱讀更多...
關于FPGA 使用SPI FLASH固化時如何配置固化參數

關于FPGA 使用SPI FLASH固化時如何配置固化參數

關于FPGA 使用SPI FLASH固化時如何配置固化參數 EDA工具&#xff1a;Vivado 關于FPGA 使用SPI FLASH固化時如何配置固化參數一、引言二、如何設置固化參數&#xff1a;使用50M的速度 &#xff0c;SPI為X4 &#xff0c;以及bit壓縮第一&#xff1a;點open implenment design第二…
閱讀更多...
Android之onMeasure的三種模式

Android之onMeasure的三種模式

Overrideprotected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {super.onMeasure(widthMeasureSpec, heightMeasureSpec);}在 Android 中&#xff0c;onMeasure() 方法是 View 或 ViewGroup 中的一個重要方法&#xff0c;用于測量視圖的大小。在 onMeasure(…
閱讀更多...
安裝軟件缺少dll文件怎么辦，分享多種解決dll問題的方法

安裝軟件缺少dll文件怎么辦，分享多種解決dll問題的方法

在計算機使用過程中&#xff0c;我們經常會遇到安裝軟件時提示缺少dll文件的問題。這種情況通常會導致軟件無法正常運行或啟動。為了解決這個問題&#xff0c;我總結了以下五種方法&#xff0c;希望對大家有所幫助。 一&#xff0c;了解DLL文件是什么 動態鏈接庫&#xff08;D…
閱讀更多...
簡單說說我對集成學習算法的一點理解

簡單說說我對集成學習算法的一點理解

概要 集成學習&#xff08;Ensemble Learning&#xff09;是一種機器學習技術框架&#xff0c;它通過構建并結合多個學習器&#xff08;也稱為個體學習器或基學習器&#xff09;來完成學習任務。 集成學習旨在通過組合多個基學習器的預測結果來提高整體模型的性能。每個基學習…
閱讀更多...
常見儀表盤指示燈的含義，這次夠全了！

常見儀表盤指示燈的含義，這次夠全了！

汽車是當前主要的交通工具之一&#xff0c;給人們的工作、生活提供了便利。大家在學會開車的同時&#xff0c;也得了解一些基本的汽車常識&#xff0c;可以及時的發現車輛的問題&#xff0c;并作出正確的判斷&#xff0c;以此降低車輛的損耗和維修成本。其中最基本的&#xff0…
閱讀更多...
房產證上加名？手把手教你操作，省錢又省心！

房產證上加名？手把手教你操作，省錢又省心！

隨著《民法典》的實施&#xff0c;房產的權屬問題愈發受到重視。夫妻雙方及其親屬常希望能在房產證上增添自己的名字&#xff0c;以保障各自的權益。那么&#xff0c;房產證上到底能寫幾個名字呢&#xff1f;以下是對這一問題的詳細解答。 一、房產證命名無固定限制 在購房時&…
閱讀更多...
準確-K8s系列文章-修改containerd 默認數據目錄

準確-K8s系列文章-修改containerd 默認數據目錄

修改 Kubernetes 集群中 containerd 默認數據目錄為 /data/containerd 前言 本文檔適用于 Kubernetes 1.24 及以上版本的集群，介紹如何將 containerd 默認的數據目錄從 /var/lib/containerd 修改為 /data/containerd。 步驟 1. 停止 containerd 服務（慎重!!!需評估風險！…
閱讀更多...
iOS中的UIScene和UISceneDelegate

iOS中的UIScene和UISceneDelegate

目錄 ???????前言 一、AppDelegate和SceneDelegate的關系 1.AppDelegate 2.SceneDelegate 3.info.plist配置 4.生命周期方法對比 1.應用啟動 2.進入前臺 3.進入后臺 5.何時使用AppDelegate和SceneDelegate 1.AppDelegate 2.SceneDelegate 前言 在iOS 13及之…
閱讀更多...
Linux內核編程入門：深度探索與實戰挑戰

Linux內核編程入門：深度探索與實戰挑戰

Linux內核編程入門&#xff1a;深度探索與實戰挑戰 在操作系統的心臟地帶&#xff0c;Linux內核以其強大、靈活和開源的特性吸引著眾多程序員。對于那些渴望深入了解系統底層機制并親手塑造操作系統的勇士們&#xff0c;Linux內核編程無疑是一個極具挑戰性和吸引力的領域。本文…
閱讀更多...
民國漫畫雜志《時代漫畫》第39期.PDF

民國漫畫雜志《時代漫畫》第39期.PDF

時代漫畫39.PDF: https://url03.ctfile.com/f/1779803-1248636473-6bd732?p9586 (訪問密碼: 9586) 《時代漫畫》的雜志在1934年誕生了&#xff0c;截止1937年6月戰爭來臨被迫停刊共發行了39期。 ps: 資源來源網絡!
閱讀更多...
Qt for Android : 使用libusb做CH340x串口傳輸的底層USB庫

Qt for Android : 使用libusb做CH340x串口傳輸的底層USB庫

簡介 Qt for Android自帶的串口方案并沒有適用在高的API版本中&#xff0c; 會出現permission denied的訪問問題&#xff0c; 所以就需要使用Android API&#xff0c; 也就是在CPP中使用JNI方式進行調用&#xff0c; 為了開發的方便&#xff0c; 使用libusb庫作為替代的底層usb…
閱讀更多...
SpringBoot注解--10--@Bean，對象注入的三種方法

SpringBoot注解--10--@Bean，對象注入的三種方法

提示&#xff1a;文章寫完后&#xff0c;目錄可以自動生成&#xff0c;如何生成可參考右邊的幫助文檔 文章目錄 Bean一、如何使用方法注解注意Bean 的命名規則&#xff0c;當沒有設置 name 屬性時&#xff0c;那么 bean 默認的名稱就是方法名&#xff0c;當設置了 name 屬性之后…
閱讀更多...
解析Java中1000個常用類：Runnable 類，你學會了嗎？

解析Java中1000個常用類：Runnable 類，你學會了嗎？

在 Java 編程中，處理并發和多線程是一個重要的主題。為了簡化多線程編程，Java 提供了多種工具和類，其中最基本的一個工具就是 Runnable 接口。 Runnable 接口為創建和管理線程提供了一種標準的方式。本文將詳細介紹 Runnable 接口的定義、實現原理、應用場景，并通過示例展…
閱讀更多...
33【Aseprite 作圖】樹——拆解

33【Aseprite 作圖】樹——拆解

1 樹葉 畫樹葉真累啊&#xff0c;可以先畫一個輪廓&#xff0c;細節一點點修 2 1 2 &#xff1b;2 2 2 &#xff08;橫著橫&#xff09;&#xff0c;這樣一點點畫樹葉 填充顏色&#xff0c;用了噴霧工具 2 樹干部分 輪廓部分&#xff0c;左邊的是3 3 3 &#xff1b;上下都是…
閱讀更多...
網頁音頻提取在線工具有哪些 網頁音頻提取在線工具下載

網頁音頻提取在線工具有哪些 網頁音頻提取在線工具下載

別再到處去借會員賬號啦。教你一招&#xff0c;無視版權和地區限制&#xff0c;直接下載網頁中的音頻文件。沒有復雜的操作步驟&#xff0c;也不用學習任何代碼。只要是網頁中播放的音頻文件&#xff0c;都可以把它下載到本地保存。 一、網頁音頻提取在線工具有哪些 市面上的…
閱讀更多...
【數據結構】二叉樹：簡約和復雜的交織之美

【數據結構】二叉樹：簡約和復雜的交織之美

專欄引入&#xff1a; 哈嘍大家好&#xff0c;我是野生的編程萌新&#xff0c;首先感謝大家的觀看。數據結構的學習者大多有這樣的想法&#xff1a;數據結構很重要&#xff0c;一定要學好&#xff0c;但數據結構比較抽象&#xff0c;有些算法理解起來很困難&#xff0c;學的很累…
閱讀更多...
Transformer中的位置編碼PE(position encoding)

Transformer中的位置編碼PE(position encoding)

Transformer中的位置編碼PE(position encoding) 1.提出背景 transformer模型的attention機制并沒有包含位置信息&#xff0c;即一句話中詞語在不同的位置時在transformer中是沒有區別的 2.解決背景 給encoder層和decoder層的輸入添加了一個額外的向量Positional Encoding&a…
閱讀更多...
平移數據c++

平移數據c++

題目描述 將a數組中第一個元素移到數組末尾,其余數據依次往前平移一個位置。 輸入 第一行為數組a的元素個數n&#xff1b; 第二行為n個小于1000的正整數。 輸出 平移后的數組元素&#xff0c;每個數用一個空格隔開。 樣例輸入 10 1 2 3 4 5 6 7 8 9 10 樣例輸出 2 3 …
閱讀更多...
【專利 超音速】一種光伏檢測系統

【專利 超音速】一種光伏檢測系統

申請號CN202410053901.0公開號&#xff08;公開&#xff09;CN118032774A申請日2024.01.12申請人&#xff08;公開&#xff09;超音速人工智能科技股份有限公司發明人&#xff08;公開&#xff09;張俊峰(總); 葉長春(總); 許春夏 摘要 本發明公開一種光伏檢測系統&#xff0…
閱讀更多...
最新文章

Copyright @ 2022~2023