【數據結構】二叉樹：簡約和復雜的交織之美

專欄引入：

哈嘍大家好，我是野生的編程萌新，首先感謝大家的觀看。數據結構的學習者大多有這樣的想法：數據結構很重要，一定要學好，但數據結構比較抽象，有些算法理解起來很困難，學的很累。我想讓大家知道的是：數據結構非常有趣，很多算法是智慧的結晶，我希望大家在學習數據結構的過程是一種愉悅的心情感受。因此我開創了《數據結構》專欄，在這里我將把數據結構內容以有趣易懂的方式展現給大家。

1.二叉樹?

?生活中，我們經常會遇到管理大量數據的情況，比如圖書館書記的分類。而二叉樹這種數據結構正是用來解決這種問題的，當我們閱讀書時，書中的每個條目都有專門分類和子分類，為了更好的組織這些內容，需要使用一種高效的數據結構來存儲和訪問信息。下面舉個簡單的例子來引入二叉樹，我們在中學學習生物時知道了植物主要分為：種子植物、苔蘚植物等。那它們是如何進行分類的呢？我們看下面這張圖片：

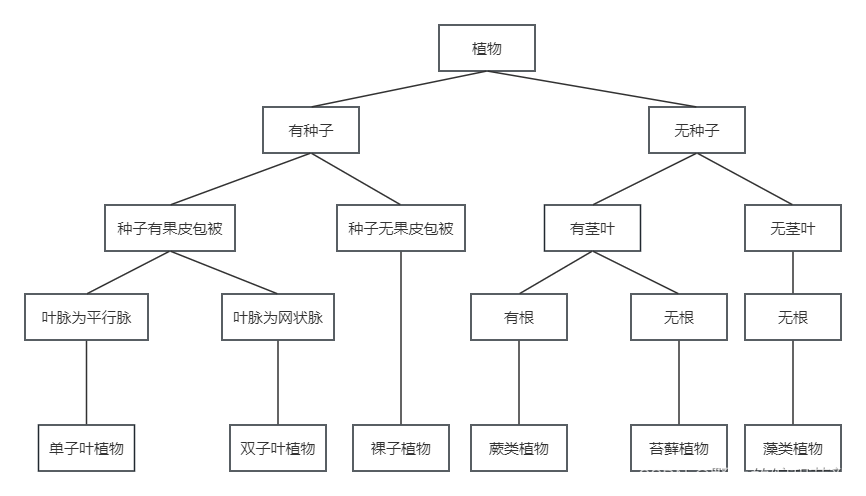
通過這種方式，我們可以逐級展開二叉樹，更詳細的組織植物分類的信息，每個節點都代表一個特定的分類，而子節點則代表該分類的下一級分類。這樣我們可以更加輕松的查找和比較不同的植物分類信息。下面我們就來揭開二叉樹的神秘面紗。

1.1二叉樹的定義

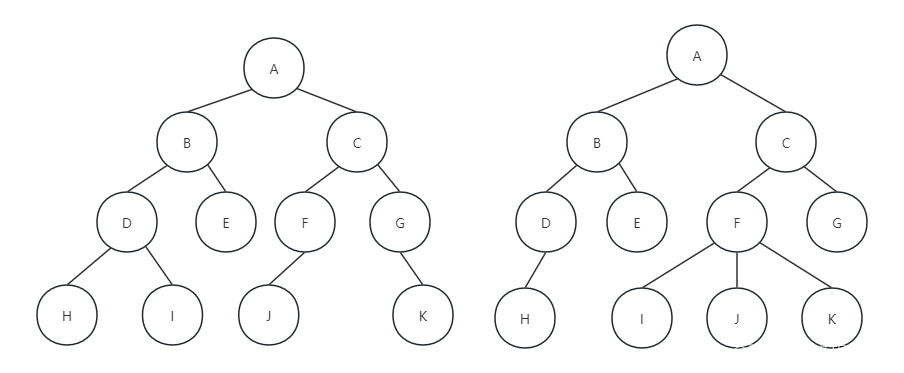
二叉樹是n（n>=0）個節點的有限集合，該集合或者為空集合（稱為空二叉樹），或者由一個根節點和兩棵互不相交的、分別稱為根節點的左子樹和右子樹的二叉樹組成。在下面的圖中，左邊的就是一棵二叉樹，而右邊的因為它的F節點有3個子節點，所以它不是二叉樹。

1.2二叉樹的特點

?二叉樹具有以下幾個特點：

每個節點最多有兩個子節點，所以二叉樹中不存在度大于2的節點。注意不是一定要有兩個節點，而是最多有兩個節點，沒有節點或者只有一個節點也是可以滴。
左子樹和右子樹是有順序的，次序不能顛倒，因此二叉樹是有序樹。
即使結構中某節點只有一個子節點，也要區分它是左節點還是右節點。

二叉樹具有以下五種基本形態：空二叉樹、只有一個根節點、根節點只有左子樹、根節點只有右子樹、根節點既有左子樹又有右子樹。

1.3特殊的二叉樹?

1.3.1斜樹

斜樹，顧名思義，斜樹一定是斜的，但是向哪里斜還是有講究的。所有節點都只有左子樹的二叉樹的叫做左斜樹，所有節點都只有右子樹的二叉樹叫做右斜樹，這兩者統稱為斜樹。在上一張圖中根節點只有左子樹和根節點只有右子樹就是左斜樹和右斜樹的一個簡單例子。斜樹也有很明顯的特點，就是每一層只有一個節點，節點個數和二叉樹的深度相同。肯定也有人好奇：這也叫樹？這不和線性表一樣嗎？確實，線性表可以理解成樹的一種極其特殊的表現形式。

1.3.2滿二叉樹

我們通常舉例子都是參差不齊的二叉樹，那是否存在完美的二叉樹呢？我們看下面這張圖片：

看來完美的二叉樹是存在的。在一棵二叉樹中，如果所有分支節點都存在左子樹和右子樹，并且所有葉子都在一層上，這樣的二叉樹叫做滿二叉樹。下面就是一個滿二叉樹，從樣子上看就感覺它很完美：

單是每一個節點都存在左右子樹，不能算滿二叉樹，還必須要所有葉子都在一層上，這樣才能做到整棵樹的平衡。因此，滿二叉樹的特點有：

葉子只能出現在最底層，出現在其他層就不能達到平衡狀態。
除了葉子節點外，每個節點都有兩個子節點。即所有非葉子節點的度都為2.
在同樣深度的二叉樹中，滿二叉樹的節點個數最多，葉子數最多。

滿二叉樹的每一層都是滿的，沒有任何缺失節點。由于每個節點都具有兩個子節點，滿二叉樹的平衡性很好。這使得在滿二叉樹上執行搜索、插入和刪除等操作的平均時間復雜度非常高效。在滿二叉樹中，從根節點到任意一個葉子節點的路徑長度都相同，是最短的路徑。滿二叉樹常用于堆數據結構。滿二叉樹在實際應用中比較少見，因為它要求節點數必須是2的冪次方，而真實的數據往往不具備這樣的特點。

1.3.3完全二叉樹

對一棵具有n個節點的二叉樹進行層序編號，如果編號為i（1≤i≤n）的節點與同樣深度的滿二叉樹中的編號為i的節點在二叉樹中的位置完全相同，則這棵二叉樹稱為完全二叉樹。如下圖：

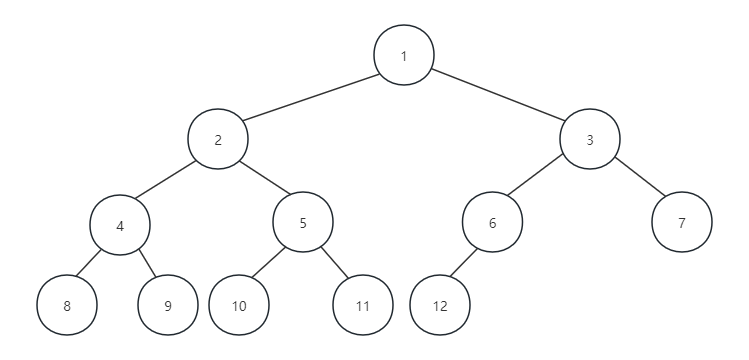
在理解時，我們要注意區分滿二叉樹和完全二叉樹。首先，從字面上區分，“完全”和“滿”的區別，滿二叉樹一定是一棵完全二叉樹，完全二叉樹不一定是滿的。其次，完全二叉樹的所有節點和同樣深度的滿二叉樹，它們按層序編號相同的節點，是一一對應的，這個關鍵詞是按層序編號。像下面的二叉樹中，因為5節點沒有右子樹，只有左子樹，使得按層序編號的第11個編號空檔了，它不是完全二叉樹：

?只有下面圖中的樹，盡管它不是滿二叉樹，但編號是連續的，所以它是完全二叉樹：

這里我們就可以總結出完全二叉樹的一些特點：

葉子節點只能出現在最后兩層。
最下層的葉子節點一定是集中在左部連續位置。
倒數第二層，如果有葉子節點，一定都在右部連續位置。
如果節點的度為1，則該節點只有左孩子，及不存在右子樹的情況。
同樣節點數的二叉樹，完全二叉樹的深度最小。

通過上面的理解，我們也知道了一個判斷二叉樹是否是完全二叉樹的方法：那就是看樹的示意圖，給每個節點按照滿二叉樹的結構逐層順序編號，如果編號出現空擋，就說明不是完全二叉樹，反之就是。完全二叉樹在實際應用中較為常見，它具有以下的優點：

節點的存儲更加高效：由于完全二叉樹的特點，可以使用數組來存儲節點。這樣可以大大節省存儲空間，因為不需要為每個節點額外存儲左右子節點的指針。
訪問效率更高：由于節點的存儲更加高效，可以使用數組的索引來訪問節點。這樣可以實現隨機訪問，訪問的時間復雜度是O(1)。而在其他類型的二叉樹中，如果要找到某個節點，需要從根節點出發進行遍歷，訪問的時間復雜度較高。

1.4二叉樹的性質?

1.4.1二叉樹的性質1

在二叉樹的第i層至多有 $2^{i-1}$ 個節點（i≥1）。這個性質很容易理解，我們觀察一下滿二叉樹：

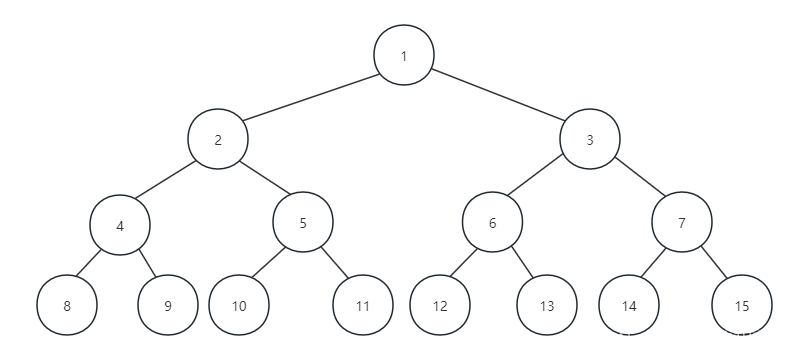
第一層是根節點，只有一個，所以 $2^{0}$ =1。第二層有兩個， $2^{1}$ =2。第三層有四個， $2^{2}$ =4。第四層有八個， $2^{3}$ =8。通過數據歸納法的論證，我們可以很輕松的得出在二叉樹的第i層上至多有 $2^{i-1}$ 個節點（i≥1）的結論。這個性質的重要性在于它給出了二叉樹的每一層上節點數量的上限。通過這個性質，我們可以更好地理解和分析二叉樹的結構。同時，這個性質也為二叉樹的遍歷、搜索等操作提供了重要的依據和限制。

1.4.2二叉樹的性質2

深度為k的二叉樹至多有 $2^{k}-1$ 個節點（k≥1）。這里一定要注意，是 $2^{k}$ 后再減1，而不是 $2^{k-1}$ 。如果不注意的話很容易和性質1搞混。深度為k也就是有k層的二叉樹，我們接著以上面那個滿二叉樹為例來看：如果只有一層，至多有 $2^{1}-1=1$ 個節點。如果只有兩層，至多有 $2^{2}-1=1+2$ 個節點。如果只有三層，至多有 $2^{3}-1=1+2+4$ 個節點。如果只有四層，至多有 $2^{4}-1=1+2+4+8$ 個節點通過數據歸納法，我們可以得出：二叉樹的深度為k層，此二叉樹至多有 $2^{k}-1$ 個節點。

1.4.3二叉樹的性質3

對于任何一棵二叉樹，如果其終端節點數為 $n_{0}$ ，度為2的節點數為 $n_{2}$ ，則 $n_{0}=n_{2}+1$ 。這是一個非常重要的性質，首先我們從二叉樹的構建過程一步一步來理解它：

首先，我們先看只有一個根節點的時候，度為0的節點個數n0=1，度為2的節點的個數為n2=0。我們設度為1的節點的個數為n1，接著，我們給根節點加一個節點，這時候一定會減少一個度為0的節點（一個度為0的節點變為度為1的節點），然后再加一個度為0的節點（新增的節點因為沒有子節點，所以增加一個度為0的節點），度為0的節點個數變化之后和之前的個數一樣，所以n0仍為1，n2仍為0。然后，我們再加一個節點，這時候會減少一個度為1的節點，然后增加一個度為0的節點和一個度為2的節點?（度為1的節點變來）。通過這個規律我們可以發現度為0的節點比度為2的節點多1個，即n0=n2+1。

同時我們也可以發現樹節點的總數為n=n0+n1+n2。通過下圖的例子，節點總數為10，它是由A、B、C、D度為2的節點，F、G、H、I、J度為0的葉子節點和E這個度為1的節點組成的。總和為4+1+5=10。

因為這個性質很重要，刷題時會經常出現考察這個性質的題，我從網上找了兩個試題來幫助大家對這個性質加深印象：

1.某二叉樹共有 399 個結點，其中有 199 個度為 2 的結點，則該二叉樹中的葉子結點數為

?（）
? ?A 不存在這樣的二叉樹

? ?B 200
? ?C 198
? ?D 199
答案：C

2.在具有 2n 個結點的完全二叉樹中，葉子結點個數為（）

??A n
? B n+1
? C n-1
? D n/2

答案：A

解析：根據題意，我們可以知道：n0+n1+n2=2n，n0=n2+1，所以n0+n1+n0-1=2n，即? ? ? ? ? ? ? ? ? ?2n0+n1-1=2n我們在接著分析這棵樹是一個完全二叉樹，所以度為1的節點個數為0或? ? ? ? ? ? ?1，因為n0、n1、n2的值為整數，所以我們可以得出n1為1，然后解開這個方程就知? ? ? ? ? ? ? ?道n0的值為n，即葉子節點個數為n。

1.4.4二叉樹的性質4?

具有n個節點的完全二叉樹的深度h=| $\log_{2}n$ |+1（這里的 |x| 表示不大于x的最大整數）。由滿二叉樹的定義我們可以知道，深度為h的滿二叉樹的節點數n一定為 $2^{h}-1$ ，因為這是最多的節點個數。那么對于n= $2^{h}-1$ 倒推可以得到滿二叉樹的深度為h= $\log (n+1)$ ，完全二叉樹我們前面也提到過，它是一棵具有n個節點的二叉樹，如果按照層序編號后與同樣深度的滿二叉樹中編號節點在二叉樹中的位置完全相同，那他就是完全二叉樹，也就是說，它的葉子節點只會出現在最下面兩層，它的節點數一定小于等于同等深度的滿二叉樹的節點數 $2^{h}-1$ ，但一定多于 $2^{h-1}-1$ ，即滿足 $2^{h-1}-1<h\leqslant 2^{h}-1$ ，由于節點數n是整數， $n\leq 2^{h}-1$ 意味著 $n< 2^{h}$ ， $n>2 ^{h-1}-1$ 意味著 $n\geq 2^{k-1}$ ，所以 $2^{h-1}\leq n< 2^{h}$ ，不等式兩邊取對數，得到 $h-1\leq \log_{2}n< h$ ，而h作為深度也是整數，因此h=| $\log_{2}n$ |+1。