關于圖的遍歷實際上就兩種
廣度優先和深度優先，一般關于圖的遍歷都是基于鄰接矩陣的，考試這些，用的也是鄰接矩陣。
本篇文章先介紹廣度優先遍歷的原理，和代碼實現
什么是圖的廣度優先遍歷？
這其實和二叉樹的層序遍歷非常相似，大家都喜歡看例子，那我就舉例子：
若對這個無向圖，從A節點開始進行廣度優先遍歷：
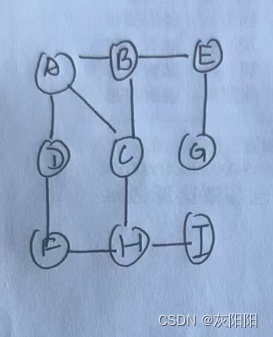
那么它的順序就應該是：
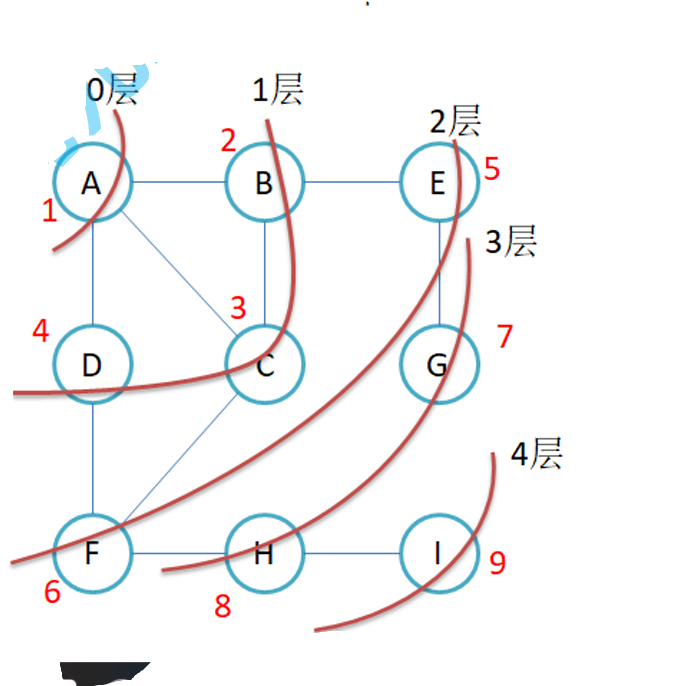
遍歷方式：
借助隊列queue，以及一個boolean類型的數組arr，用來記錄頂點是否已經訪問：
public void traverse(char v){//需要的頂點Queue<Character> queue=new LinkedList<>();/** vertexS是儲存所有頂點的字符數組* _getIndexOfV(傳入一個字符（頂點）)---->這個函數可以獲得對應vertexS數組的下標* * */boolean[] visited=new boolean[vertexS.length];//定義，用來標記是否已近訪問queue.offer(v);while(!queue.isEmpty()){char vertex= queue.poll();//出隊列，一個System.out.print(vertex);//直接打印int index=_getIndexOfV(vertex);//獲得下標visited[index]=true;//出隊列就要置為空for (int i = 0; i < vertexS.length ; i++) {//遍歷第index行的（在當前頂點周圍搜索是否有頂點鏈接）if(matrix[index][i]!=0&&!visited[i]){queue.offer(vertexS[i]);//入隊列visited[i]=true;//入隊就要標記，免得等一下重復入隊，造成嚴重后果}}if(!queue.isEmpty()){//不為空就加一個箭頭System.out.print(" -> ");}}}以這個圖作為測試：
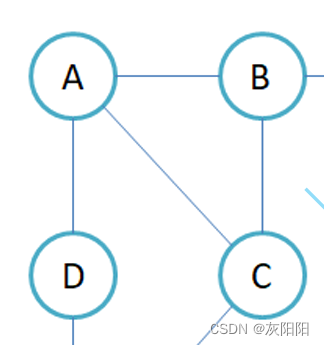
public class Test {public static void main(String[] args) {char[] array = {'A', 'B', 'C', 'D','E'};GrapByMatrix grap = new GrapByMatrix(array, false);grap.addEdge('A', 'B', 1);grap.addEdge('A', 'D', 1);grap.addEdge('B', 'C', 1);grap.addEdge('A', 'C', 1);grap.traverse('A');}
}
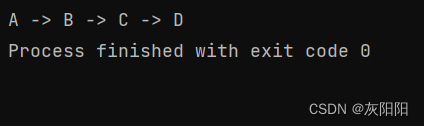
執行結果：
)
