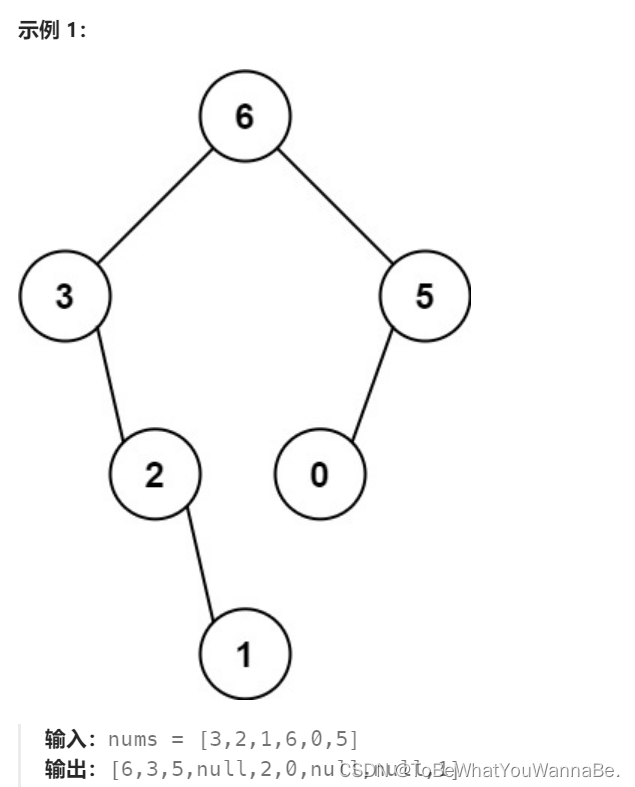
654. 最大二叉樹

給定一個不重復的整數數組 nums 。 最大二叉樹 可以用下面的算法從 nums 遞歸地構建:

創建一個根節點，其值為 nums 中的最大值。
遞歸地在最大值 左邊 的 子數組前綴上 構建左子樹。
遞歸地在最大值 右邊 的 子數組后綴上 構建右子樹。
返回 nums 構建的 最大二叉樹 。

方法一：遞歸

class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {return construct(nums, 0, nums.length - 1);}public TreeNode construct(int[] nums, int left, int right) {if (left > right) {return null;}int best = left;for (int i = left + 1; i <= right; ++i) {if (nums[i] > nums[best]) {best = i;}}TreeNode node = new TreeNode(nums[best]);node.left = construct(nums, left, best - 1);node.right = construct(nums, best + 1, right);return node;}
}

這段代碼定義了一個名為 Solution 的類，其中有兩個方法用于構建一棵最大二叉樹。最大二叉樹的定義是：樹中的每個節點都是對應輸入數組中從該節點所在位置開始往后的子數組中的最大值。以下是代碼的詳細解釋：

1. public TreeNode constructMaximumBinaryTree(int[] nums) 是主要接口，接收一個整型數組 nums，并返回根據該數組構建的最大二叉樹的根節點。它通過調用重載的 construct 方法來實現這個功能，初始化傳入整個數組的起始下標 0 和結束下標 nums.length - 1。

2. public TreeNode construct(int[] nums, int left, int right) 是一個遞歸方法，用于根據輸入數組 nums 從索引 left 到 right 的子數組構建最大二叉樹。

   • 首先，檢查邊界條件，如果 left > right，表示當前子數組為空，沒有節點可構建，返回 null。
   • 然后，在 left 到 right 的范圍內找到最大值的索引 best。初始化時假設 best 為 left，通過遍歷該范圍內的元素，如果發現更大的值，則更新 best。
   • 創建一個新的 TreeNode，其值為 nums[best]，即當前子數組中的最大值。
   • 遞歸調用 construct 方法構建左子樹，參數為 left 和 best - 1，意在構建以當前最大值左側子數組為基礎的最大二叉樹。
   • 同樣遞歸調用構建右子樹，參數為 best + 1 和 right，構建以當前最大值右側子數組為基礎的最大二叉樹。
   • 最后，返回當前節點，完成以 nums[best] 為根節點的子樹構建。

通過這樣的遞歸過程，代碼能夠高效地遍歷整個數組，構建出整棵最大二叉樹。這種方法充分利用了分治思想，每次遞歸調用都確保了以當前區間的最大值為根節點，從而保證了構建出的二叉樹滿足題目要求。

方法二：單調棧

class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {int n = nums.length;Deque<Integer> stack = new ArrayDeque<Integer>();int[] left = new int[n];int[] right = new int[n];Arrays.fill(left, -1);Arrays.fill(right, -1);TreeNode[] tree = new TreeNode[n];for (int i = 0; i < n; ++i) {tree[i] = new TreeNode(nums[i]);while (!stack.isEmpty() && nums[i] > nums[stack.peek()]) {right[stack.pop()] = i;}if (!stack.isEmpty()) {left[i] = stack.peek();}stack.push(i);}TreeNode root = null;for (int i = 0; i < n; ++i) {if (left[i] == -1 && right[i] == -1) {root = tree[i];} else if (right[i] == -1 || (left[i] != -1 && nums[left[i]] < nums[right[i]])) {tree[left[i]].right = tree[i];} else {tree[right[i]].left = tree[i];}}return root;}
}

這段代碼實現了一個名為 Solution 的類，其中的 constructMaximumBinaryTree 方法接收一個整型數組 nums，并根據這個數組構建一棵最大二叉樹。最大二叉樹的特性是每個節點都是其子樹（包括該節點）中最大值的節點。與之前遞歸的解法不同，這段代碼采用了單調棧和兩次遍歷的方法來構造這棵樹。

代碼邏輯步驟如下：

1. 初始化變量和數據結構：

   • n 為數組 nums 的長度。
   • stack 是一個單調遞減的整數棧，用于存放數組下標，保證棧頂元素對應的 nums 值是棧中已處理元素中的最大值。
   • left 和 right 數組分別記錄每個元素在最大二叉樹中的左孩子和右孩子的索引，初始化為 -1。
   • tree 數組用于存儲根據 nums 創建的 TreeNode 對象。

2. 第一次遍歷：

   • 遍歷 nums 數組，創建每個節點并壓入棧中。同時，根據棧的狀態更新每個節點的左右孩子索引（在 left 和 right 數組中記錄）。
   • 當遇到一個比棧頂元素值更大的數時，說明棧頂元素右邊的節點已經找到，更新相應索引，并將棧頂元素出棧，直到棧為空或遇到比當前元素小的值。這保證了棧中元素按照最大二叉樹的右邊界逆序排列。

3. 構建最大二叉樹：

   • 根據 left 和 right 數組以及棧中元素的關系，第二次遍歷數組，為每個節點分配左右子樹。這里通過判斷條件確定當前節點應作為其父節點的左子樹還是右子樹，最后找到根節點（其左右孩子索引均為 -1）。

4. 返回根節點：構建完成后，返回 root，即整個最大二叉樹的根節點。

這種方法避免了遞歸調用，利用棧和兩次遍歷數組的方式，實現了從給定數組直接構建最大二叉樹的功能，時間復雜度為 O(n)，空間復雜度也為 O(n)。

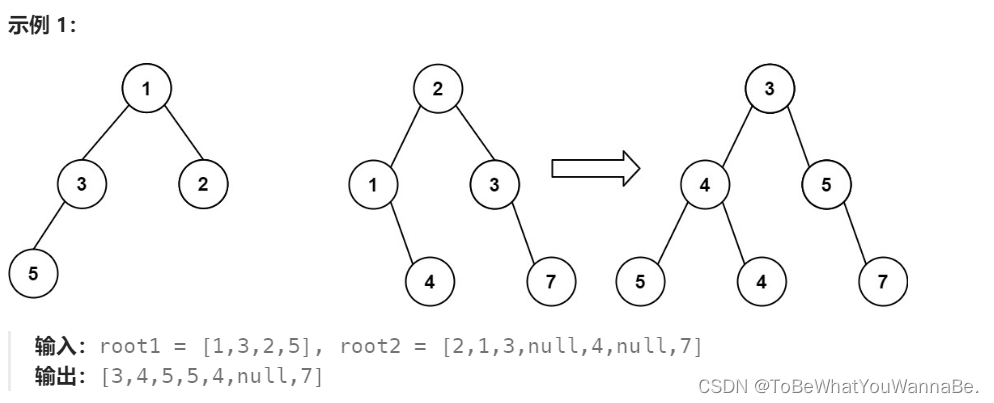
617. 合并二叉樹

方法一：深度優先搜索

class Solution {public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {if (t1 == null) {return t2;}if (t2 == null) {return t1;}TreeNode merged = new TreeNode(t1.val + t2.val);merged.left = mergeTrees(t1.left, t2.left);merged.right = mergeTrees(t1.right, t2.right);return merged;}
}

這段代碼定義了一個名為 Solution 的類，其中包含一個方法 mergeTrees，用于合并兩棵二叉樹 t1 和 t2。合并規則是：如果兩個節點重疊，那么它們的值相加作為新節點的值；非空節點與空節點相遇時，非空節點將被保留。該方法遞歸地實現了這一過程，具體步驟如下：

1. 基本情況檢查：

   • 首先，如果 t1 為空，直接返回 t2，表示當前子樹以 t2 為準。
   • 如果 t2 為空，直接返回 t1，表示當前子樹以 t1 為準。

2. 創建合并節點：

   • 如果兩個節點都不為空，創建一個新的 TreeNode，其值為 t1.val + t2.val，這表示合并了兩個節點的值。

3. 遞歸合并子樹：

   • 對于新節點的左子樹，遞歸調用 mergeTrees(t1.left, t2.left)，將 t1 和 t2 的左子樹合并，并將結果賦給新節點的左子指針。
   • 對于新節點的右子樹，遞歸調用 mergeTrees(t1.right, t2.right)，將 t1 和 t2 的右子樹合并，并將結果賦給新節點的右子指針。

4. 返回合并后的節點：

   • 最終，返回新創建的合并節點，這樣就完成了從當前節點開始的整個子樹的合并。

通過這樣的遞歸處理，整棵樹被自頂向下地合并，直至所有節點都被正確處理，最終返回合并后樹的根節點。這種方法簡潔而高效，適合解決這類二叉樹合并的問題。

方法二：廣度優先搜索

class Solution {public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {if (t1 == null) {return t2;}if (t2 == null) {return t1;}TreeNode merged = new TreeNode(t1.val + t2.val);Queue<TreeNode> queue = new LinkedList<TreeNode>();Queue<TreeNode> queue1 = new LinkedList<TreeNode>();Queue<TreeNode> queue2 = new LinkedList<TreeNode>();queue.offer(merged);queue1.offer(t1);queue2.offer(t2);while (!queue1.isEmpty() && !queue2.isEmpty()) {TreeNode node = queue.poll(), node1 = queue1.poll(), node2 = queue2.poll();TreeNode left1 = node1.left, left2 = node2.left, right1 = node1.right, right2 = node2.right;if (left1 != null || left2 != null) {if (left1 != null && left2 != null) {TreeNode left = new TreeNode(left1.val + left2.val);node.left = left;queue.offer(left);queue1.offer(left1);queue2.offer(left2);} else if (left1 != null) {node.left = left1;} else if (left2 != null) {node.left = left2;}}if (right1 != null || right2 != null) {if (right1 != null && right2 != null) {TreeNode right = new TreeNode(right1.val + right2.val);node.right = right;queue.offer(right);queue1.offer(right1);queue2.offer(right2);} else if (right1 != null) {node.right = right1;} else {node.right = right2;}}}return merged;}
}

這段代碼同樣定義了一個名為 Solution 的類，其中的 mergeTrees 方法用于合并兩棵二叉樹 t1 和 t2，但與之前的遞歸解法不同，這里采用的是廣度優先搜索（BFS）的方法。具體步驟如下：

1. 基本情況檢查：

   • 首先檢查 t1 和 t2 是否為空，與之前一樣，如果一方為空，則直接返回另一方。

2. 初始化合并后的樹：

   • 創建一個新的樹節點 merged，其值為 t1.val + t2.val。

3. 初始化隊列：

   • 定義三個隊列，分別用于存儲當前層待處理的合并后節點、t1 的節點和 t2 的節點。初始時，將 merged 及其對應的 t1 和 t2 根節點分別加入各自的隊列。

4. 廣度優先遍歷并合并：

   • 使用 while 循環處理隊列，直到 queue1 和 queue2 都為空。
   • 每次循環，從隊列中彈出當前層的 merged 節點、t1 的節點和 t2 的節點。
   • 對于左子樹和右子樹，如果有任何一個非空，則創建或直接引用新的節點進行合并：
     • 若 t1 和 t2 的子節點都非空，則創建新節點，值為兩個子節點的值之和，然后將新節點分別加入合并后的樹、queue1 和 queue2。
     • 若只有一個非空，則直接將非空的子節點掛接到合并后的樹上。

5. 返回合并后的樹：

   • 遍歷完成后，返回最初的合并節點 merged，即合并后的二叉樹的根節點。

這種方法通過層序遍歷的方式合并兩棵樹，同樣能有效地合并兩棵二叉樹，但相比于遞歸解法，它在處理大量樹節點時可能會占用更多內存，因為需要同時維護多個隊列來存儲每層的節點。不過，它提供了一種迭代而非遞歸的視角來解決問題，增加了算法實現的多樣性。

700. 二叉搜索樹中的搜索

給定二叉搜索樹（BST）的根節點 root 和一個整數值 val。

你需要在 BST 中找到節點值等于 val 的節點。 返回以該節點為根的子樹。 如果節點不存在，則返回 null 。

方法一：遞歸

class Solution {public TreeNode searchBST(TreeNode root, int val) {if (root == null) {return null;}if (val == root.val) {return root;}return searchBST(val < root.val ? root.left : root.right, val);}
}

這段代碼定義了一個名為 Solution 的類，其中包含一個方法 searchBST。該方法在一個二叉搜索樹（BST）中查找值為 val 的節點，并返回找到的節點。如果沒有找到，則返回 null。方法使用了遞歸的方式來實現搜索邏輯。下面是詳細的步驟解釋：

1. 基本情況檢查：首先檢查當前節點 root 是否為空。如果為空，說明樹中沒有找到值為 val 的節點，因此返回 null。

2. 匹配節點值：接下來，比較當前節點 root 的值與其要查找的值 val。如果兩者相等，即找到了目標節點，直接返回當前節點 root。

3. 選擇遞歸方向：如果當前節點的值不等于 val，則根據 BST 的性質（左子樹所有節點的值小于根節點，右子樹所有節點的值大于根節點），決定下一步搜索的方向：

   • 如果 val 小于當前節點值 root.val，則向左子樹 (root.left) 繼續搜索。
   • 如果 val 大于當前節點值 root.val，則向右子樹 (root.right) 繼續搜索。

   這里使用了條件運算符（三元運算符）來簡潔地表達這一選擇邏輯。

4. 遞歸調用：根據選擇的方向，遞歸調用 searchBST 方法，并將搜索結果返回。由于每次遞歸調用都更接近目標值或最終確定目標不存在（當遇到空節點時），因此這個過程是逐步縮小搜索范圍直至找到目標或遍歷完可能的路徑。

通過上述遞歸過程，該方法能夠高效地在二叉搜索樹中查找指定值的節點。

方法二：迭代

class Solution {public TreeNode searchBST(TreeNode root, int val) {while (root != null) {if (val == root.val) {return root;}root = val < root.val ? root.left : root.right;}return null;}
}

這段代碼同樣定義了一個名為 Solution 的類，其中包含一個方法 searchBST，用于在一個二叉搜索樹（BST）中查找值為 val 的節點。與之前的遞歸實現不同，這里采用的是迭代方法來遍歷樹并查找目標節點。下面是該方法的詳細解釋：

1. 循環條件與初始化：使用一個 while 循環來遍歷樹，直到找到目標節點或遍歷完整個樹（即 root 變為 null）。

2. 查找并返回匹配節點：在循環體內，首先檢查當前節點 root 的值是否等于 val。如果相等，說明找到了目標節點，直接返回該節點。

3. 決定遍歷方向：如果當前節點的值不等于 val，根據二叉搜索樹的性質選擇遍歷方向：

   • 如果 val 小于當前節點值 root.val，則向左子樹移動，即令 root = root.left。
   • 如果 val 大于當前節點值 root.val，則向右子樹移動，即令 root = root.right。

4. 循環結束：如果循環結束時仍未找到匹配的節點（即 root 變為 null），則返回 null，表示樹中不存在值為 val 的節點。

通過這樣的迭代過程，該方法能夠高效地在二叉搜索樹中查找指定值的節點，且相比遞歸實現，它在某些情況下（尤其是樹深度大時）可以減少調用棧的空間消耗。

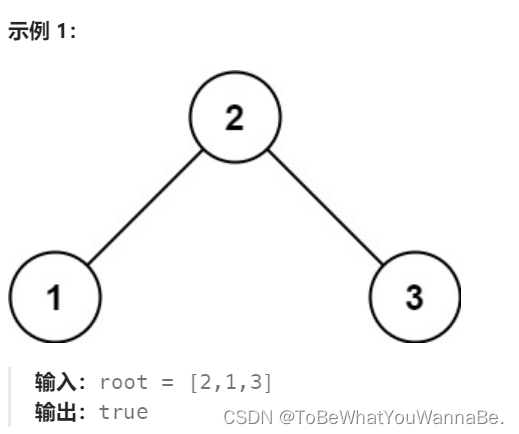
98. 驗證二叉搜索樹

給你一個二叉樹的根節點 root ，判斷其是否是一個有效的二叉搜索樹。

有效 二叉搜索樹定義如下：

節點的左
子樹
只包含 小于 當前節點的數。
節點的右子樹只包含 大于 當前節點的數。
所有左子樹和右子樹自身必須也是二叉搜索樹。

方法一: 遞歸

class Solution {public boolean isValidBST(TreeNode root) {return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);}public boolean isValidBST(TreeNode node, long lower, long upper) {if (node == null) {return true;}if (node.val <= lower || node.val >= upper) {return false;}return isValidBST(node.left, lower, node.val) && isValidBST(node.right, node.val, upper);}
}

這段代碼定義了一個名為 Solution 的類，其中包含一個公共方法 isValidBST 用于檢查給定的二叉樹是否是一棵有效的二叉搜索樹（BST）。二叉搜索樹的特性是對于任意節點，其左子樹中所有節點的值都嚴格小于該節點的值，其右子樹中所有節點的值都嚴格大于該節點的值。此外，還定義了一個重載的輔助方法 isValidBST，用于遞歸校驗每個節點是否滿足BST的條件，并且傳遞了當前節點值允許的最小值 lower 和最大值 upper 作為邊界條件。

具體邏輯如下：

1. 公共方法 isValidBST：這是用戶調用的接口，接收樹的根節點 root 作為參數。它通過調用重載的輔助方法 isValidBST 來進行實際的驗證工作，初始化 lower 為 Long.MIN_VALUE（Java中的最小長整型值，確保任何合法節點值都大于它），upper 為 Long.MAX_VALUE（Java中的最大長整型值，確保任何合法節點值都小于它）。

2. 輔助方法 isValidBST：

   • 基本情況：如果當前節點 node 為空，說明已遍歷到樹的底部，返回 true 表示這一分支是有效的。
   • 檢查節點值：如果當前節點的值不在允許的范圍內（即 node.val <= lower 或 node.val >= upper），說明違反了BST的規則，返回 false。
   • 遞歸驗證：對當前節點的左子樹和右子樹進行遞歸驗證。左子樹的每個節點值必須小于當前節點值，因此傳遞當前節點值作為下一次遞歸的上限 upper=node.val；右子樹的每個節點值必須大于當前節點值，所以傳遞當前節點值作為下一次遞歸的下限 lower=node.val。只有當左右子樹都滿足BST條件時，整個樹才被認為是有效的BST，因此這里使用邏輯與操作 && 連接兩個遞歸調用的結果。

通過這樣的遞歸策略，代碼能夠高效地遍歷整個二叉樹，同時在每個遞歸層級上檢查節點值是否滿足BST的定義，從而確定給定的二叉樹是否是一個有效的二叉搜索樹。

方法二：中序遍歷

class Solution {public boolean isValidBST(TreeNode root) {Deque<TreeNode> stack = new LinkedList<TreeNode>();double inorder = -Double.MAX_VALUE;while (!stack.isEmpty() || root != null) {while (root != null) {stack.push(root);root = root.left;}root = stack.pop();// 如果中序遍歷得到的節點的值小于等于前一個 inorder，說明不是二叉搜索樹if (root.val <= inorder) {return false;}inorder = root.val;root = root.right;}return true;}
}

這段代碼定義了一個名為 Solution 的類，其中包含一個公共方法 isValidBST，用于判斷給定的二叉樹是否為有效的二叉搜索樹（BST）。與之前的遞歸解法不同，這里采用迭代方法，利用棧來實現中序遍歷。下面是代碼的詳細解析：

1. 初始化：聲明一個 Deque（雙端隊列）stack 用于存放待訪問的節點，以及一個 double 類型的變量 inorder 初始化為負無窮大，用于存儲中序遍歷過程中訪問過的節點值（用于檢查BST性質）。

2. 迭代遍歷：使用一個 while 循環，條件為棧非空或當前根節點 root 非空，確保遍歷完整個二叉樹。

   • 左子樹入棧：在循環內部，首先不斷將當前節點 root 的左子節點壓入棧中，直到沒有左子節點，這步是為了確保每次處理的節點都是當前子樹的最左節點，即中序遍歷的順序。

   • 處理當前節點：當左子節點為空時，從棧頂彈出節點作為當前節點 root，并檢查其值是否大于 inorder。如果不大于（即小于等于），說明違背了BST的性質（中序遍歷下嚴格遞增），直接返回 false。

   • 更新 inorder：如果當前節點值符合BST性質，則更新 inorder 為當前節點值，準備與下一個節點比較。

   • 轉向右子樹：最后，將當前節點更新為其右子節點，繼續遍歷。

3. 遍歷結束判斷：當遍歷完整個樹（棧為空且當前 root 也為空）后，說明所有節點都滿足BST的條件，返回 true。

這種方法通過迭代實現了二叉樹的中序遍歷，并在遍歷過程中實時檢查每個節點的值是否滿足BST的定義，是一種空間效率較高的算法，因為它只需要常數級別的額外空間（除了存儲樹本身的棧空間）。