異方差的Stata操作（計量114）

以數據集 nerlove.dta 為例，演示如何在 Stata 中處理異方差。

此數據集包括以下變量：

tc ( 總成本 ) ；

q ( 總產量 ) ；

pl ( 工資率 ) ；

pk ( 資本的使用成本 ) ；

pf ( 燃料價格 ) ；

相應的對數值 lntc 、 lnq 、 lnpl 、 lnpk 、 lnpf

1.畫殘差圖

通過觀察殘差圖，如果殘差隨著擬合值或某個解釋變量的變化而呈現系統性的變化趨勢（如增大或減小），則可能表明存在異方差性。異方差性意味著誤差項的方差不是常數，而是隨著某些變量的變化而變化。

首先，以 OLS 估計對數形式的成本函數：

use nerlove.dta,clear

reg lntc lnq lnpl lnpk lnpf

完成回歸后，可使用以下命令得到殘差圖：

rvfplot? ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (residual-versus-fitted plot)

rvpplot varname? ? ? ? ? ? ? ? ? ? ? ? (residual-versus-predictor plot)

varname ：是變量的名字，把它代稱自己數據的名字。

初步考察異方差，畫殘差與擬合值的散點圖：? ? ? ? rvfplot

? ? ? ? ?? 當總成本 (lntc 的擬合值 ) 較小時，擾動項的方差較大。
考察殘差與解釋變量 lnq 的散點圖：? ? ? ? ? ? ? ? ? ?? rvpplot lnq

? ? ? ? ? ?當產量 (lnq) 越小時，擾動項的方差越大。

初步判斷是復雜性的異方差

2.BP檢驗

BP檢驗的基本思想是通過檢驗殘差的平方與自變量之間是否存在顯著的相關關系來判斷模型的異方差性。在標準的線性回歸模型中，假設誤差項（即殘差）的方差是恒定的。然而，在實際應用中，這一假設可能不成立，即存在異方差性。BP檢驗通過構建一個輔助回歸模型來檢驗這種異方差性。

在 Stata 中完成回歸后，可使用以下命令進行 BP檢驗：

hettest // 對所有變量進行 BP 檢驗? ? ? ? ?

或：estat hettest,iid rhs

其中，“ estat ”指 post-estimation statistics( 估計后統計量 )，即在完成估計后所計算的后續統計量。

“hettest” 表示 heteroskedasticity test 。

選擇項 ”iid” 表示僅假定數據為 iid （獨立同分布），而無須正態假定。

選擇項”rhs”表示使用方程右邊的全部解釋變量進行輔助回歸，默認使用擬合值?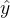 $\hat{y}$ ?進行輔助回歸。

如想指定使用某些解釋變量進行輔助回歸，可使用命令：

hettest variable // 對指定變量進行 BP 檢驗

或： estat hettest [varlist],iid

其中， ”[varlist]” 為指定的變量清單；而 ”[ ]”表示其中的內容可出現在命令中，也可不出現。

回到 Nerlove(1963)的例子：
quietly reg lntc lnq lnpl lnpk lnpf? ? ? ?//其中，前綴(prefix) ”quietly”表示執行此命令，但不在Stata的結果窗口顯示運行結果

首先，使用擬合值? $\hat{y}$ ?進行 BP 檢驗:?? ? ?? ?estat hettest, iid

其次，使用所有解釋變量進行 BP 檢驗：??estat hettest, iid rhs

最后，使用變量 lnq 進行 BP 檢驗：? ? ? ????estat hettest lnq,iid

各種形式 BP 檢驗的 𝑝 值都等于 0.0000，故強烈拒絕同方差的原假設，認為存在異方差。

3.懷特檢驗

基本思想是如果模型存在異方差性，那么殘差的平方應該與模型的解釋變量有關。
構造一個輔助回歸模型，以殘差的平方作為因變量，將原始回歸模型中的解釋變量及其平方項和交叉項作為自變量。如果輔助回歸模型的解釋變量對殘差平方沒有影響，即原假設成立，那么輔助回歸模型的R平方應該很小。

在 Stata 完成回歸后，可使用如下命令進行懷特檢驗：??

whitetst

或： estat imtest,white

其中， ”imtest” 指 information matrix test( 信息矩陣檢驗 ) 。

繼續以Nerlove(1963)為例：
estat imtest,white

?4.穩健標準誤

穩健標準誤在 Stata 中十分簡單，在命令 reg之后加選擇項加“ robust ”即可

reg lntc lnq lnpl lnpk lnpf, robust? ? ? ? ? // 截面數據

reg lntc lnq lnpl lnpk lnpf, vce(hc2)? ? ? // 小樣本下，更穩健

reg lntc lnq lnpl lnpk lnpf, vce(hc3)? ? ? // 小樣本下，更穩健

混合截面數據或面板數據，應使用?vce (cluster clustvar) 選項。

5.FGLS （可行的GLS估計量）

糾正異方差的 FGLS 程序：

① 利用估計模型? 𝑦 = 𝛽 0 + 𝛽 1 𝑥 1 + 𝛽 2 𝑥 2 + ? + 𝛽 𝑘 𝑥 𝑘 + 𝜇 得到 OLS 的殘差? $\hat{\mu }$

② 對殘差? $\hat{\mu }$ ?進行平方，然后再取自然對數得到 log( $\hat{\mu }^{2}$ )

③ 利用log( $\hat{\mu }^{2}$ )對 𝑥 1 , 𝑥2, … . , 𝑥𝑘進行回歸，得到擬合值?? $\hat{g}$

④ 獲得擬合值的指數： $\hat{h}=exp (\hat{g})$

⑤ 以 1/ $\hat{h}$ ?為權數，用 WLS 估計方程 𝑦 = 𝛽 0 + 𝛽 1 𝑥 1 + 𝛽 2 𝑥 2 + ? + 𝛽 𝑘 𝑥 𝑘 + 𝜇

得到擾動項方差的估計值? $\hat{\sigma} _{i}^{2}$ ?后，可作為權重進行 WLS 估計。

假設? $\hat{\sigma} _{i}^{2}$ ?存儲在變量 var 上，可通過如下 Stata 命令來實現 WLS ：

reg y x1 x2 x3 [aw=1/var]

其中，“ aw” 表示 analytical weight ，為擾動項方差 (不是標準差 ) 的倒數。

繼續以 Nerlove(1963)為例。
首先計算殘差，并記為 e1 ：

quietly reg lntc lnq lnpl lnpk lnpf

predict e1,residual
其次，生成殘差的平方，并記為 e2：

gen e2=e1^2
將殘差平方取對數，

gen lne2=log(e2)

假設? $ln\hat{\sigma} _{i}^{2}$ ? 為變量 lnq 的線性函數，進行輔助回歸：

reg lne2 lnq lnpl lnpk lnpf
計算輔助回歸的擬合值，并記為 lne2f：

predict lne2f
去掉對數后，即得到方差的估計值，并記為 e2f ：

gen e2f=exp(lne2f)
使用方差估計值的倒數作為權重，進行 WLS 回歸：

reg lntc lnq lnpl lnpk lnpf [aw=1/e2f]

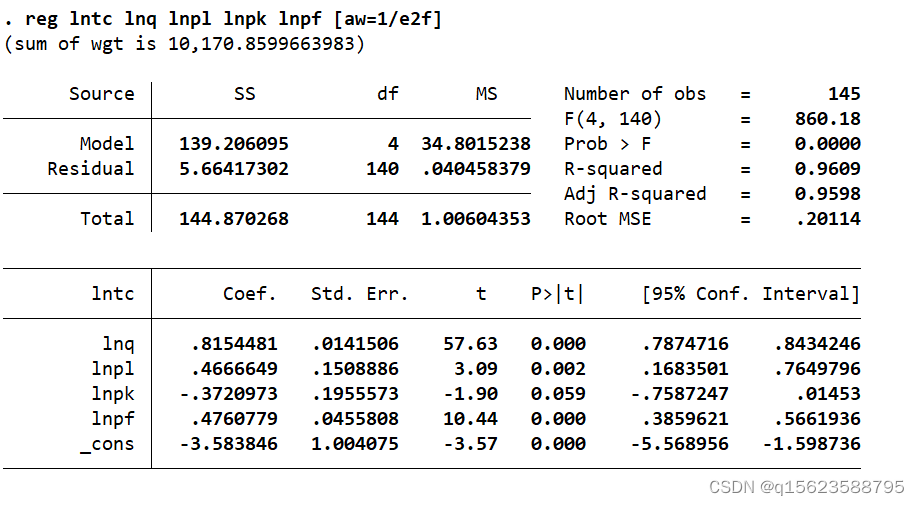
使用 OLS 時，變量 lnpl 的 𝑝 值為 0.13 ，在 10%的水平上也不顯著；使用 WLS 后，該變量的 𝑝值變為 0.002 ，在 1% 的水平上顯著不為 0 。

由于 Nerlove(1963)數據存在明顯的異方差，使用WLS 后提高了估計效率。

如擔心條件方差函數的設定不準確，導致加權后的新擾動項仍有異方差，可使用穩健標準誤進行 WLS 估計：?reg lntc lnq lnpl lnpk lnpf [aw=1/e2f],r

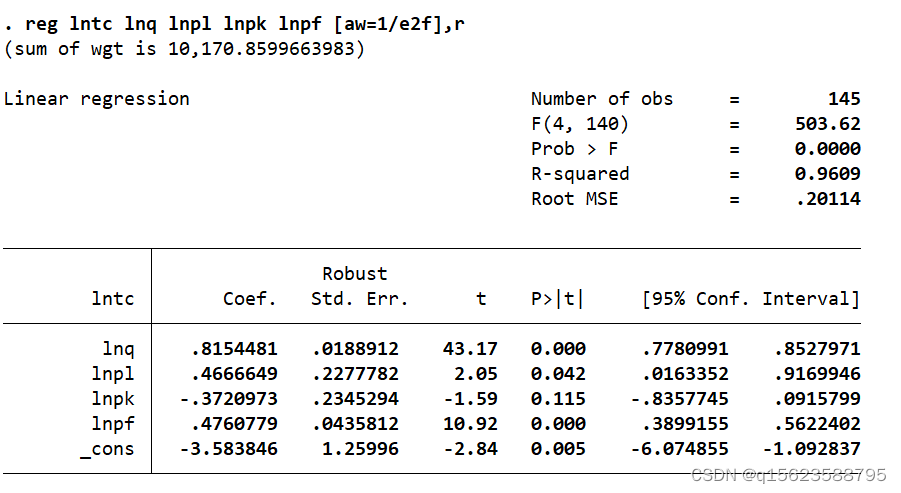
無論是否使用穩健標準誤， WLS 的回歸系數都相同，但標準誤有所不同。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/bicheng/16359.shtml
繁體地址，請注明出處：http://hk.pswp.cn/bicheng/16359.shtml
英文地址，請注明出處：http://en.pswp.cn/bicheng/16359.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！