圖_基礎算法

圖這種數據結構還有一些比較特殊的算法，比如二分圖判斷，有環圖無環圖的判斷，拓撲排序，以及最經典的最小生成樹，單源最短路徑問題，更難的就是類似網絡流這樣的問題。

先看拓撲排序（有環無環）：la總微信文章的鏈接：https://mp.weixin.qq.com/s?__biz=MzAxODQxMDM0Mw==&mid=2247491897&idx=1&sn=c2d77dd649548d077815af3c976b61d1&scene=21#wechat_redirect
然后看二分圖
然后看并查集
然后最小生成樹dijkstra 單源最短路徑

基本概念：

大部分都是以鄰接表的形式存儲：

// 記得每一個都要初始化一下為new ArrayList<>()或者LinkedList;
List<Integer>[] graph;

拓撲排序

拓撲排序的對象，就是有向無環圖（DAG）。一個有向無環圖的拓撲排序結果不止一種。

給定一個包含 n個節點的有向圖 G，我們給出它的節點編號的一種排列，如果滿足：

對于圖 G 中的任意一條有向邊 (u,v)，u 在排列中都出現在 v的前面。

那么稱該排列是圖 G 的「拓撲排序」

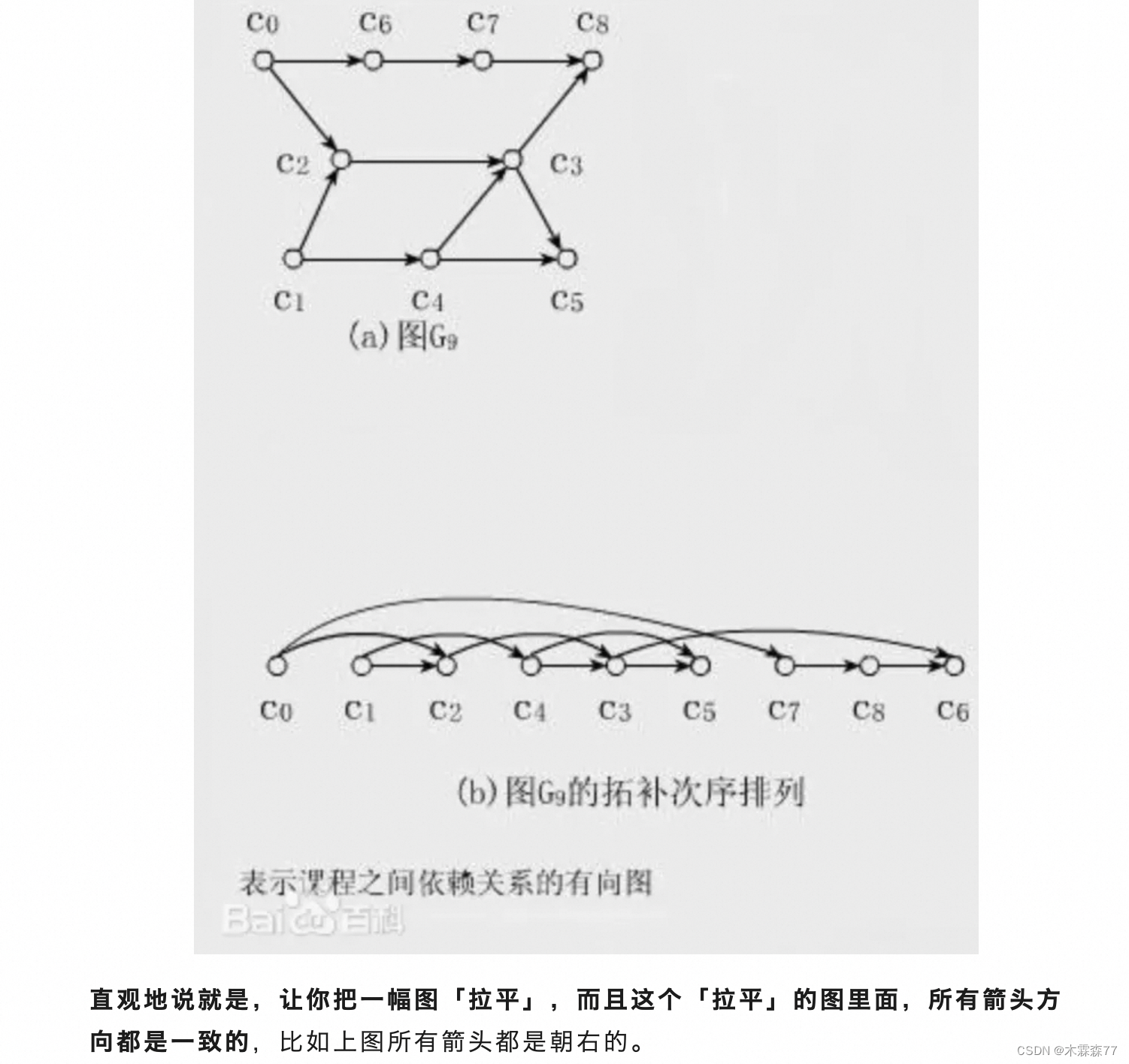
在這里插入圖片描述

先說一下怎么判斷圖有沒有環（力扣207 課程表）。
BFS很簡單，直接把所有入度為0的入隊列遍歷一遍，adj度數減1，要是入度為0就繼續入隊列，最后還有度數不為0的節點（也可以每次遍歷queue計數，最后判斷計數結果等不等于n），就說明有環。

// 207題 BFS實現
class Solution {public boolean canFinish(int numCourses, int[][] prerequisites) {int[] indegrees = new int[numCourses];List<List<Integer>> adjacency = new ArrayList<>();Queue<Integer> queue = new LinkedList<>();// 初始化圖for(int i = 0; i < numCourses; i++)adjacency.add(new ArrayList<>());// 注意cp[0]前置為cp[1]，所以先上cp[1]才能繼續走到cp[0]，即 箭頭指向為1->0for(int[] cp : prerequisites) {indegrees[cp[0]]++;adjacency.get(cp[1]).add(cp[0]);}// 把所有入度為0的加進來for(int i = 0; i < numCourses; i++)if(indegrees[i] == 0) queue.add(i);// 開始bfswhile(!queue.isEmpty()) {int pre = queue.poll();numCourses--;for(int cur : adjacency.get(pre))// 別忘了減入度if(--indegrees[cur] == 0) queue.add(cur);}// 根據n是否減為0判斷是否全部節點都被遍歷了一遍，如果有環就說明n不為0return numCourses == 0;}
}

dfs判斷的方式更簡單了，在開始進入遍歷cur的adj之前 標記onPath為true，遍歷完adj之后把onPath恢復為false（恢復現場）。下一次遞歸開始時發現onPath已經為true就說明有環，類似貪吃蛇咬到了自己。
onPath數組和visited數組可以合為一個數組，用int標識不同的情況。例如初始化flag數組都是0，然后進入遞歸置為1，結束遞歸置為-1.這樣，每次進入一個節點的時候就判斷如果flag==-1就返回；flag為1就說明有環。

// DFS判斷是否有環
boolean[] onPath;boolean hasCycle = false;
boolean[] visited;void traverse(List<Integer>[] graph, int curIndex) {if (onPath[curIndex]) {// 發現環！！！hasCycle = true;}if (visited[curIndex]) {return;}// 將節點 s 標記為已遍歷visited[curIndex] = true;// 開始遍歷節點 sonPath[curIndex] = true;for (int adj : graph[curIndex]) {traverse(graph, adj);}// 節點 s 遍歷完成onPath[curIndex] = false;
}

注意由于可能一次traverse并不能遍歷完所有的節點，所以要遍歷nums，從0-n都當成curIndex傳入。

// 207課程表 dfs實現判斷是否有環，以flag為標識 return true或者false
class Solution {public boolean canFinish(int numCourses, int[][] prerequisites) {List<List<Integer>> adjacency = new ArrayList<>();for(int i = 0; i < numCourses; i++)adjacency.add(new ArrayList<>());int[] flags = new int[numCourses];for(int[] cp : prerequisites)adjacency.get(cp[1]).add(cp[0]);for(int i = 0; i < numCourses; i++)if(!dfs(adjacency, flags, i)) return false;return true;}private boolean dfs(List<List<Integer>> adjacency, int[] flags, int i) {if(flags[i] == 1) return false;if(flags[i] == -1) return true;flags[i] = 1;for(Integer j : adjacency.get(i))if(!dfs(adjacency, flags, j)) return false;flags[i] = -1;return true;}
}

然后借機說一下遞歸怎么進行拓撲排序，以力扣的210課程表II 為例，由于有依賴的前置課程，所以我們要先完成依賴的課程，也就是樹的根節點。再代入后序遍歷的思路，拓撲排序的結果其實就是這個多叉樹后序遍歷的數組反轉之后的結果。
當然，如果要實現拓撲排序，前提一定是要先判斷是否有環的。可以在遍歷的時候判斷，也可以直接把207的代碼copy過來

boolean[] visited;
// 記錄后序遍歷結果
List<Integer> postorder = new ArrayList<>();int[] findOrder(int numCourses, int[][] prerequisites) {// 先保證圖中無環if (!canFinish(numCourses, prerequisites)) {return new int[]{};}// 建圖List<Integer>[] graph = buildGraph(numCourses, prerequisites);// 進行 DFS 遍歷visited = new boolean[numCourses];for (int i = 0; i < numCourses; i++) {traverse(graph, i);}// 將后序遍歷結果反轉，轉化成 int[] 類型Collections.reverse(postorder);int[] res = new int[numCourses];for (int i = 0; i < numCourses; i++) {res[i] = postorder.get(i);}return res;
}void traverse(List<Integer>[] graph, int s) {if (visited[s]) {return;}visited[s] = true;for (int t : graph[s]) {traverse(graph, t);}// 后序遍歷位置postorder.add(s);
}

為什么310的最小高度樹的解法（把入度為1也就是葉子結點入隊列然后每次去掉一圈葉子結點之后就是根節點了）是拓撲排序，可能是因為滿足拓撲排序的性質：后序遍歷。

并查集 Union-Find

并查集比較簡單，也可以直接用并查集判斷是否有環，這里直接附上并查集的代碼

class UF {private int count;private int parent[];public UF(int n) {parent = new int[n+1];// 初始化的時候 全都是獨立的根節點 指向自己for (int i = 0; i <= n; i++) {parent[i] = i;}// 計數countcount = n;}public int getUFCount() {return count;}public int findRoot(int x) {// 注意回溯的話要用if。循環的話要用whileif (parent[x] != x) {parent[x] = findRoot(parent[x]);}return parent[x];/*while (parent[x] != x) {// 進行路徑壓縮parent[x] = parent[parent[x]];x = parent[x];}return x;*/}public void union(int a, int b) {int rootA = findRoot(a);int rootB = findRoot(b);if (rootA == rootB) {return;}parent[rootA] = rootB;// 別忘了count--count--;}public boolean connected(int a, int b) {return findRoot(a) == findRoot(b);}}

并查集相關題目：
785 判斷二分圖
1319 連通網絡的操作次數這題用UF做可以；用DFS類似于判斷拓撲排序是否有環也可以，具體看一下題解。
886 可能的二分法

在這里插入圖片描述

二分圖

接著說一下二分圖

定義：如果能將一個圖的節點集合分割成兩個獨立的子集 A 和 B ，并使圖中的每一條邊的兩個節點一個來自 A 集合，一個來自 B 集合，就將這個圖稱為二分圖。

二分圖也可以用并查集UF來解決，把所有cur的adj都union,遍歷某個adj的時候如果發現adj和cur已經相連了connected了，就說明不可分為兩個獨立子集。
例題：785 判斷二分圖
還有一種就是染色法，遍歷adj如果未染色就染成和cur不一致的顏色，如果發現adj顏色不是初始狀態且和cur顏色一致，就說明不可二分。

染色可以初始化RED/BLUE之類的，也可以直接用int標識。例如0；1；-1

/*** BFS廣度優先遍歷-染色法** @param graph* @return*/private boolean useBfs(int[][] graph) {int n = graph.length;Deque<Integer> queue = new ArrayDeque<>(n);// 用visit數組表示染色，visited[i]為0表示還未被染色，初次染色為1，其鄰接點染色時被賦值為-1int visited[] = new int[n];// 每個節點未被染色前都要進隊列for (int i = 0; i < n; i++) {if (visited[i] != 0) {continue;}visited[i] = 1;queue.addLast(i);while (!queue.isEmpty()) {int item = queue.removeFirst();for (int adj : graph[item]) {// 未被染色 就處理為-visited[item];if (visited[adj] == 0) {visited[adj] = -visited[item];queue.addLast(adj);}// 已被染色且和當前顏色相等 就返回falseelse if (visited[adj] == visited[item]) {return false;}}}}return true;}

最小生成樹

Kruskal 算法

一開始的時候就把所有的邊排序，然后從權重最小的邊開始挑選屬于最小生成樹的邊，組建最小生成樹。

prim算法

原理：對于任意一個節點，切分他的連接點之后，橫切邊上權重最小的邊，一定是構成最小生成樹的一條邊。
實現：用優先級隊列結合BFS動態獲取權重最小邊
為了防止重復切，需要用一個變量判斷是否已經被加入過結果集（最小生成樹）中了。
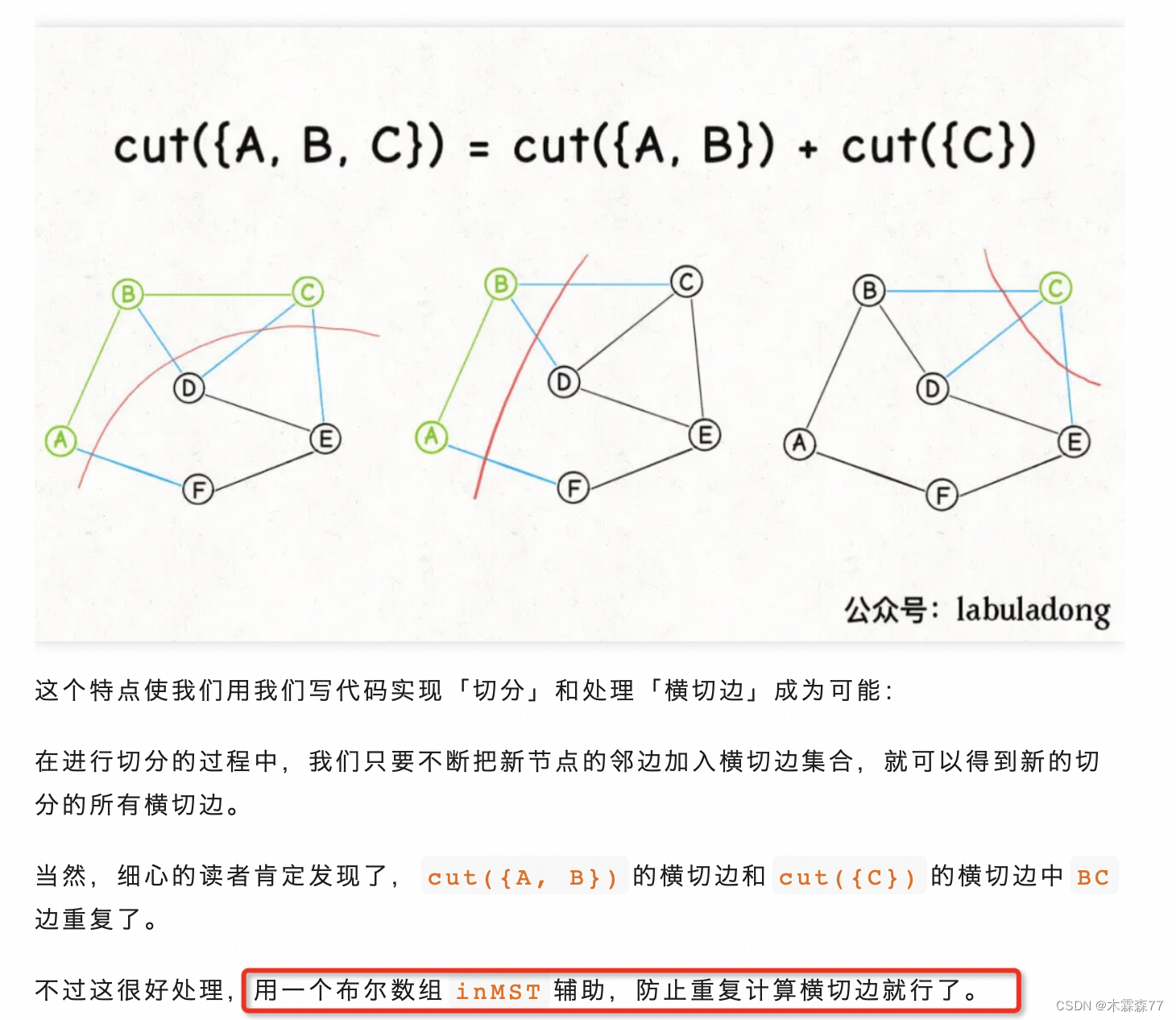
在這里插入圖片描述

class Prim {// 核心數據結構，存儲「橫切邊」的優先級隊列private PriorityQueue<int[]> pq;// 類似 visited 數組的作用，記錄哪些節點已經成為最小生成樹的一部分private boolean[] inMST;// 記錄最小生成樹的權重和private int weightSum = 0;// graph 是用鄰接表表示的一幅圖，// graph[s] 記錄節點 s 所有相鄰的邊，// 三元組 int[]{from, to, weight} 表示一條邊private List<int[]>[] graph;public Prim(List<int[]>[] graph) {this.graph = graph;this.pq = new PriorityQueue<>((a, b) -> {// 按照邊的權重從小到大排序return a[2] - b[2];});// 圖中有 n 個節點int n = graph.length;this.inMST = new boolean[n];// 隨便從一個點開始切分都可以，我們不妨從節點 0 開始inMST[0] = true;cut(0);// 不斷進行切分，向最小生成樹中添加邊while (!pq.isEmpty()) {int[] edge = pq.poll();int to = edge[1];int weight = edge[2];if (inMST[to]) {// 節點 to 已經在最小生成樹中，跳過// 否則這條邊會產生環continue;}// 將邊 edge 加入最小生成樹weightSum += weight;inMST[to] = true;// 節點 to 加入后，進行新一輪切分，會產生更多橫切邊cut(to);}}// 將 s 的橫切邊加入優先隊列private void cut(int s) {// 遍歷 s 的鄰邊for (int[] edge : graph[s]) {int to = edge[1];if (inMST[to]) {// 相鄰接點 to 已經在最小生成樹中，跳過// 否則這條邊會產生環continue;}// 加入橫切邊隊列pq.offer(edge);}}// 最小生成樹的權重和public int weightSum() {return weightSum;}// 判斷最小生成樹是否包含圖中的所有節點public boolean allConnected() {for (int i = 0; i < inMST.length; i++) {if (!inMST[i]) {return false;}}return true;}
}

dijkstra最短路徑

說到了這里，狄杰斯特拉算法其實非常簡單，就是一個BFS算法的進階使用，先用一個對象State保存當前節點ID、距離start節點的距離distFromStart。每次用優先級隊列，按照distFromStart從小到大排序。然后遍歷隊列中cur的adj，把最小路徑加入結果集中即可。

// 返回節點 from 到節點 to 之間的邊的權重
int weight(int from, int to);// 輸入節點 s 返回 s 的相鄰節點
List<Integer> adj(int s);// 輸入一幅圖和一個起點 start，計算 start 到其他節點的最短距離
int[] dijkstra(int start, List<Integer>[] graph) {// 圖中節點的個數int V = graph.length;// 記錄最短路徑的權重，你可以理解為 dp table// 定義：distTo[i] 的值就是節點 start 到達節點 i 的最短路徑權重int[] distTo = new int[V];// 求最小值，所以 dp table 初始化為正無窮Arrays.fill(distTo, Integer.MAX_VALUE);// base case，start 到 start 的最短距離就是 0distTo[start] = 0;// 優先級隊列，distFromStart 較小的排在前面Queue<State> pq = new PriorityQueue<>((a, b) -> {return a.distFromStart - b.distFromStart;});// 從起點 start 開始進行 BFSpq.offer(new State(start, 0));while (!pq.isEmpty()) {State curState = pq.poll();int curNodeID = curState.id;int curDistFromStart = curState.distFromStart;if (curDistFromStart > distTo[curNodeID]) {// 已經有一條更短的路徑到達 curNode 節點了continue;}// 將 curNode 的相鄰節點裝入隊列for (int nextNodeID : adj(curNodeID)) {// 看看從 curNode 達到 nextNode 的距離是否會更短int distToNextNode = distTo[curNodeID] + weight(curNodeID, nextNodeID);if (distTo[nextNodeID] > distToNextNode) {// 更新 dp tabledistTo[nextNodeID] = distToNextNode;// 將這個節點以及距離放入隊列pq.offer(new State(nextNodeID, distToNextNode));}}}return distTo;
}

這里有一個優化點，不用visited數組判斷是否會走回頭路，因為每個adj都先判斷加上cur-adj的權重之后是否小于之前已加入結果集的最小路徑，小的話才會更新結果集并加入隊列。
因為兩個節點之間的最短距離（路徑權重）肯定是一個確定的值，不可能無限減小下去，所以隊列一定會空，不會無限循環。隊列空了之后，distTo數組中記錄的就是從start到其他節點的最短距離。

上述代碼是為了找到從start到所有節點的最小路徑（結果集為distTo[]），如果指定了到end節點，在while循環中判斷curNodeId==end即可結束while循環,return curDistFromStart（因為每次從優先級隊列中拿出來的一定是最小的路徑權重）。

相關題目：
743 題「網絡延遲時間
第 1514 題「概率最大的路徑」

看一下1631 最小體力消耗路徑應該和并查集、二分、dijkstra最短路徑都有關系