鏈表的合并

題目描述

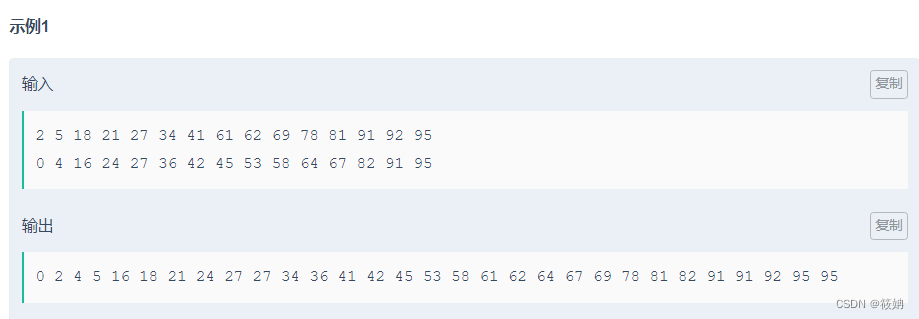
運行代碼

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{  int a[31];for(int i = 1;i <= 30;i++)cin>>a[i];sort(a + 1,a + 1 + 30);for(int i = 1;i < 30;i++)cout<<a[i]<<" ";cout<<a[30]<<endl;return 0;
}

代碼思路

1. 定義數組：定義了一個大小為31的整數數組a，但實際上我們只使用前30個位置（從a[1]到a[30]）。在C++中，數組通常從索引0開始，但這里為了某種原因（可能是題目要求或其他原因），代碼從索引1開始。
2. 輸入數據：使用for循環從標準輸入讀取30個整數，并將它們存儲在數組a的索引1到30中。
3. 排序數據：使用std::sort函數對數組進行排序。注意，這里傳遞給sort函數的是數組的起始地址和結束地址（不包括結束地址對應的元素）。
4. 輸出數據：使用for循環輸出排序后的數組元素。但是，這里有一個小錯誤：循環的條件是i < 30，這意味著它會輸出索引從1到29的元素，而遺漏了索引為30的元素。
5. 輸出最后一個元素：在for循環之后，單獨輸出索引為30的元素。

改進代碼

1. 數組索引：為了與C++的常規做法保持一致，并避免潛在的錯誤，最好從索引0開始使用數組。這樣，你就不需要為數組分配額外的空間，也不需要記住從哪個索引開始讀取或寫入數據。
2. 輸出循環：為了簡潔起見，可以將輸出索引為30的元素的代碼移到for循環中。這樣，你就不需要單獨處理最后一個元素了。

#include<iostream>  
#include<algorithm>  
using namespace std;   
int main()  
{  int a[30]; // 直接定義大小為30的數組  for(int i = 0; i < 30; i++) // 從索引0開始讀取數據  cin >> a[i];  sort(a, a + 30); // 直接使用數組的起始和結束地址  for(int i = 0; i < 30; i++) // 從索引0開始輸出數據  cout << a[i] << " ";  cout << endl; // 在循環后直接輸出換行符  return 0;  
}

?兌換零錢

題目描述

運行代碼

#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int mod=1e9+7;
int a[20]={1,2,5,10,20,50,100,200,500,1000,2000,5000,10000},dp[100010];
int main()
{dp[0]=1;for(int i=0;i<13;i++)for(int j=a[i];j<=100000;j++)dp[j]=(dp[j]+dp[j-a[i]])%mod;int N,T;cin>>T;while( T-- ){cin>>N;cout<<dp[N]<<endl;}return 0;
}

代碼思路

1. 初始化dp[0]為1，因為湊成面額0只有一種方式（即不使用任何硬幣）。
2. 使用兩個嵌套的循環來計算dp數組的其他元素。外層循環遍歷硬幣數組a，內層循環遍歷從當前硬幣面額到100000的所有可能面額。對于每個面額j，我們都檢查是否可以使用當前硬幣a[i]來湊成它。如果可以（即j >= a[i]），則dp[j]的值是原來的值加上dp[j-a[i]]（即不使用當前硬幣和使用當前硬幣的湊法數之和）。
3. 最后，程序讀取測試用例數量T，然后對每個測試用例讀取一個整數N，并輸出dp[N]，即湊成面額N的方法數。

改進建議

1. 避免使用<bits/stdc++.h>：這個頭文件雖然包含了幾乎所有標準庫，但它不是標準C++的一部分，而且會增加編譯時間。建議只包含你需要的頭文件。
2. 數組大小：雖然這里定義dp數組的大小為100010是足夠的，但如果你想要一個更通用的解決方案，你可以根據輸入的最大可能值來動態分配這個數組的大小。
3. 輸入驗證：雖然在這個問題中可能不需要，但在實際應用中，驗證輸入的有效性（例如，確保N是非負的）是一個好習慣。
4. 注釋：添加注釋來解釋代碼的每個部分是如何工作的，以及為什么選擇這種特定的實現方式，可以幫助其他人（或未來的你）更容易地理解代碼。
5. 優化：雖然對于這個問題來說，當前的實現已經足夠快，但如果你在處理更大的面額或更多的硬幣時，你可能需要考慮更高效的算法，如使用背包問題的優化技術。

改進代碼

#include <iostream>  
#include <vector>  
using namespace std;  
const int MOD = 1e9 + 7;  
const int MAX = 100000; 
vector<int> coin = {1, 2, 5, 10, 20, 50, 100, 200, 500, 1000, 2000, 5000, 10000};  
// 動態規劃表，用于存儲湊成不同面額的方法數  
vector<int> Amount(MAX + 1, 0);  
int main() {  // 初始化湊成面額0的方法數為1  Amount[0] = 1;   // 動態規劃計算湊成不同面額的方法數  for (int i = 0; i < coin.size(); i++) {  for (int j = coin[i]; j <= MAX; j++) {  Amount[j] = (Amount[j] + Amount[j - coin[i]]) % MOD;  }  }  int T, N;  cin >> T; // 讀取測試用例數量   while (T--) {  cin >> N; // 讀取當前測試用例的面額  cout <<Amount[N] << endl; // 輸出湊成面額N的方法數  }   return 0;  
}