1.二叉樹的遍歷
2.二叉樹鏈式結構的實現
3.解決單值二叉樹題
1.二叉樹的遍歷
1.1前序,中序以及后序遍歷
二叉樹的遍歷是按照某種特定的規則,依次對二叉樹的結點進行相應的操作,并且每個結點只操作一次。
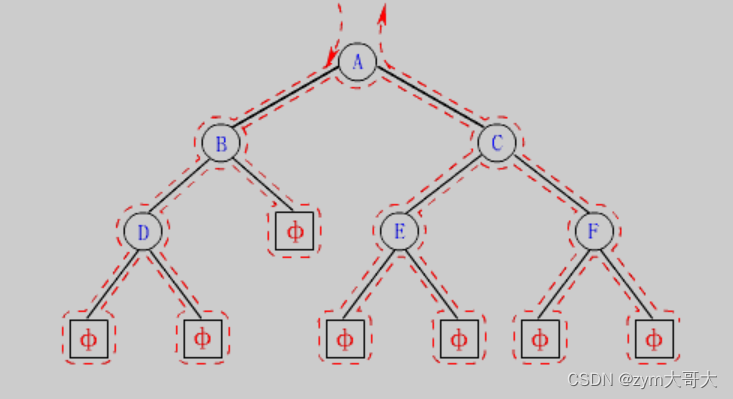
二叉樹的遍歷有這些規則:前序/中序/后序/的遞歸結構遍歷
1.前序遍歷:先訪問根結點,再訪問左子樹,最后訪問右子樹
2.中序遍歷:先訪問左子樹,再訪問根結點,最后訪問右子樹
3.后序遍歷:先訪問左子樹,再訪問右子樹,最后根結點?
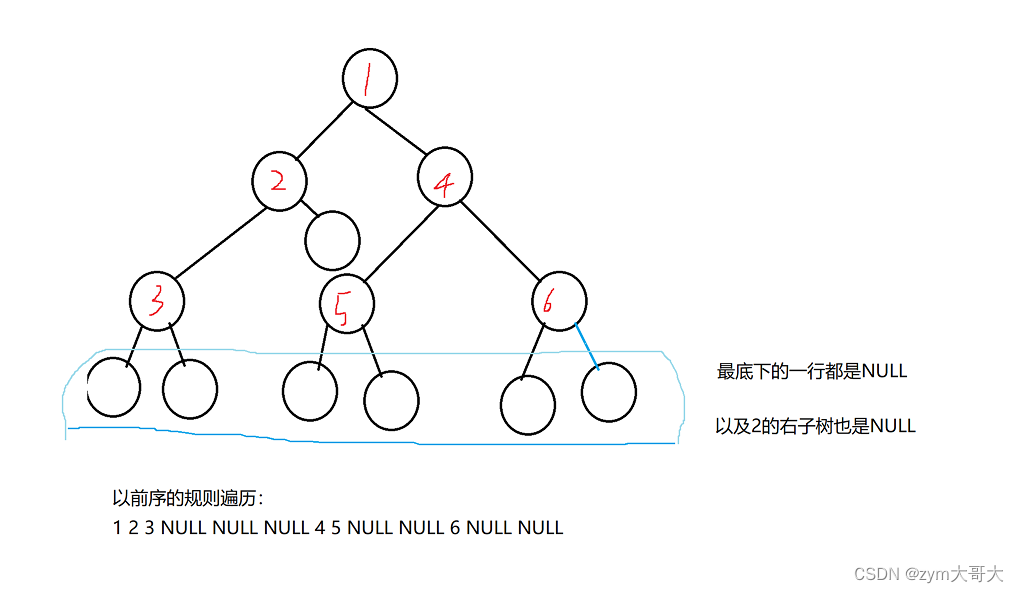
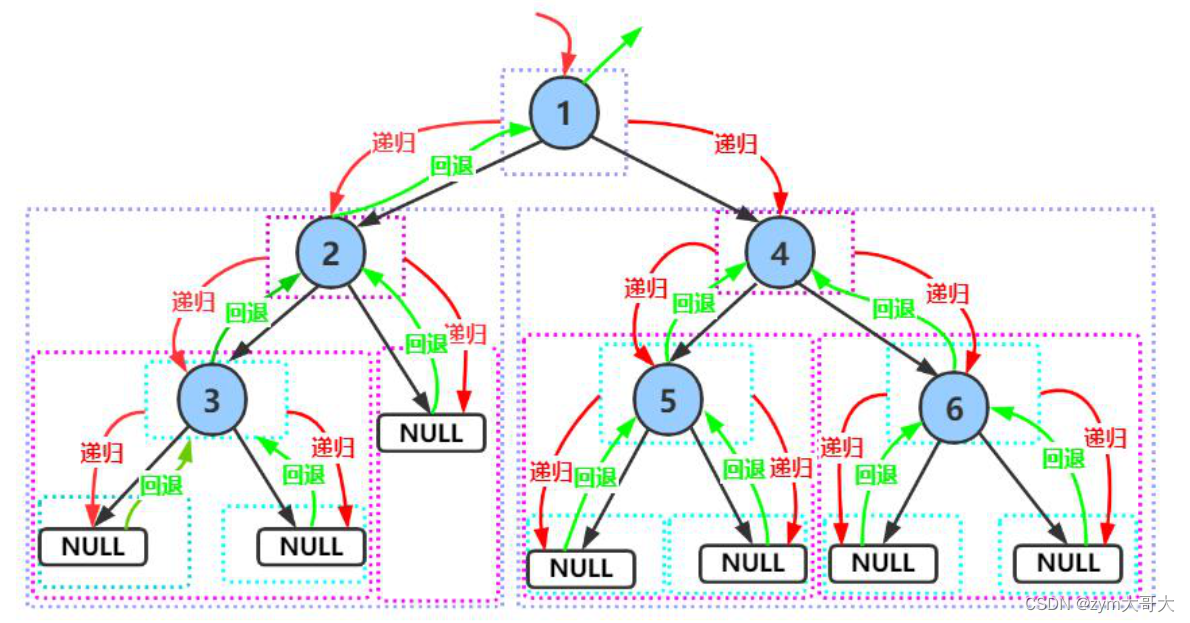
以前序的規則來遍歷二叉樹,進入1結點(值為1的結點),1結點為根結點所以先訪問,然后是左子樹也就是2結點,此時進入2結點后,2結點是根結點,先訪問2結點再訪問左子樹3結點,進入3結點后,以3結點作為根結點,先訪問3結點,后訪問3結點的左子樹,此時就到最后一行都是NULL結點,訪問完NULL結點后(3結點的左子樹),就訪問3結點的右子樹(NULL結點),這時候3結點已訪問完,而3結點又是2結點的左子樹,也就是說2結點的左子樹訪問完,就訪問2結點的右子樹(NULL結點),2結點也訪問完了,2結點又是1結點的左子樹,既1結點的左子樹訪問完,開始訪問1結點的右子樹,后續過程也是一樣的,每進入一個結點都是新的根結點,按照前序的遍歷,總的看就是一個遞歸過程了,只有3結點的左右子樹以及自身被訪問完后才去訪問上面結點的右子樹。
 ?
?
?
 ?
?
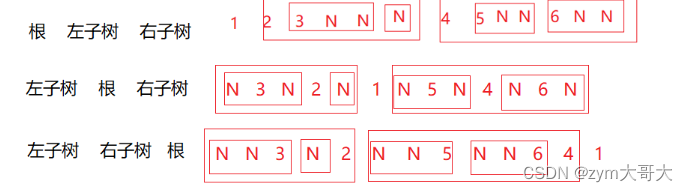
?訪問的順序不同也會帶來不同的特點,前序訪問則第一個是最上面的結點,中序訪問最上面的結點會把其的左右子數分成倆邊,后序則最上面的結點在最后面,中序和后序的過程與前序差不多,就是根結點的訪問有所不同。
?2.二叉樹鏈式結構的實現
2.1代碼實現遍歷二叉樹數
下面是以前序為規則遍歷的代碼實現:
#include<stdio.h>
#include<stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;BinaryTreeNode* left;BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(int x)
{BTNode* a = (BTNode*)malloc(sizeof(BTNode));if (a == NULL){perror("malloc fail:");return NULL;}a->data = x;a->left = NULL;a->right = NULL;return a;
}
BTNode* CreatNode()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}
void PrevOver(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOver(root->left);PrevOver(root->right);
}
int main()
{BTNode* root = CreatNode();PrevOver(root);return 0;
}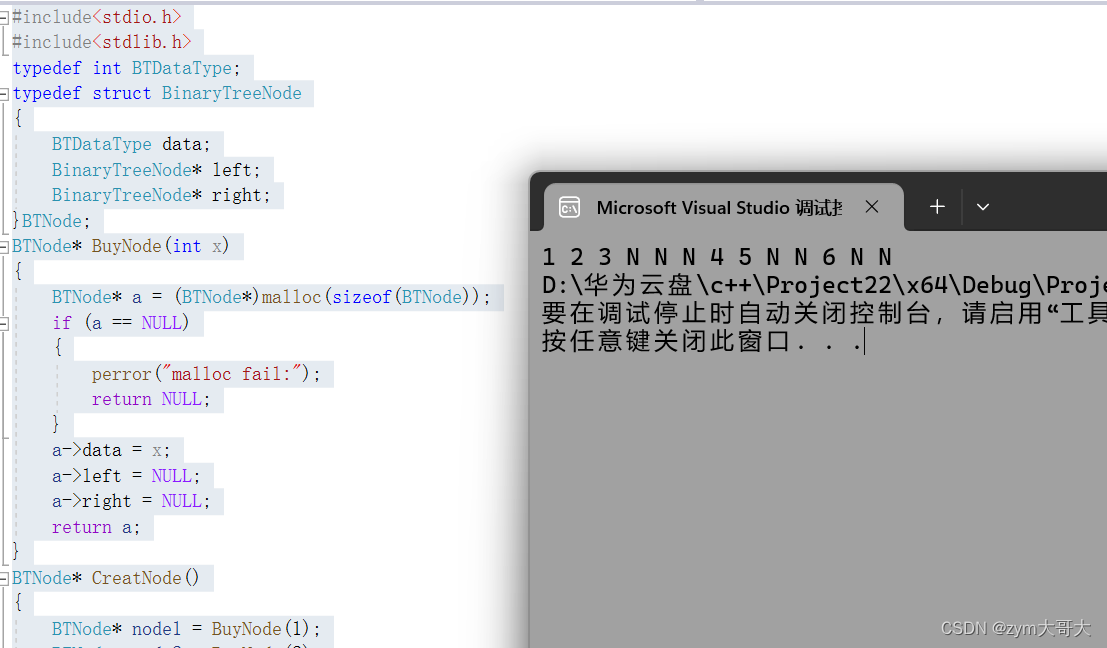
結果如上面分析的一樣。
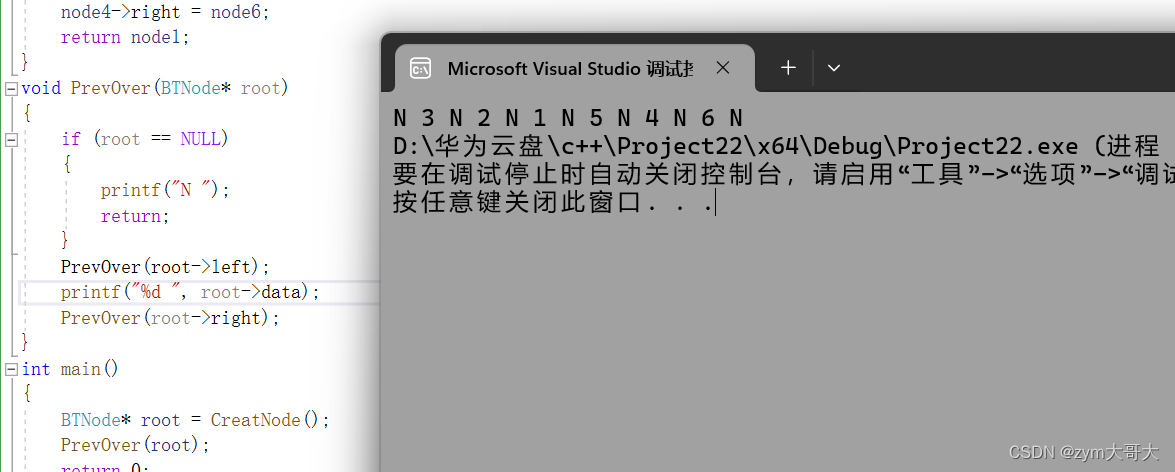
只需要改變 PrevOver函數中代碼的順序就可以切換成其他的規則的遍歷,把左子樹放在根的訪問前就是中序的遍歷規則。
2.2實現計算二叉樹中的結點的個數
錯誤代碼1:
int TreeNode(BTNode* root)
{int size = 0;if (root == NULL){return 0;}++size;TreeNode(root->left);TreeNode(root->right);return size;
}首先size是在棧區上開辟的空間,當出了這個函數,棧區就會被銷毀,函數只會傳size的值,size變量是被銷毀了,但是沒有接受返回的值,等于是去銀行取錢,結果忘記拿錢了,這樣是找不到累計的效果的,需要理解的是不是名字一樣就是同一個變量,在遞歸的過程中,雖然都是size但是這些size是在不同棧區上開辟的不同變量,只是名字相同,所以最后返回的size是第一次調用的函數的size,最后會返回1.
錯誤代碼2:
通過static可以是局部變量在出函數時不會被銷毀掉,保留size的值,使得size能達到計數的效果,
但是也有缺陷,就是在主函數中多次調用計算結點數量的函數會出問題
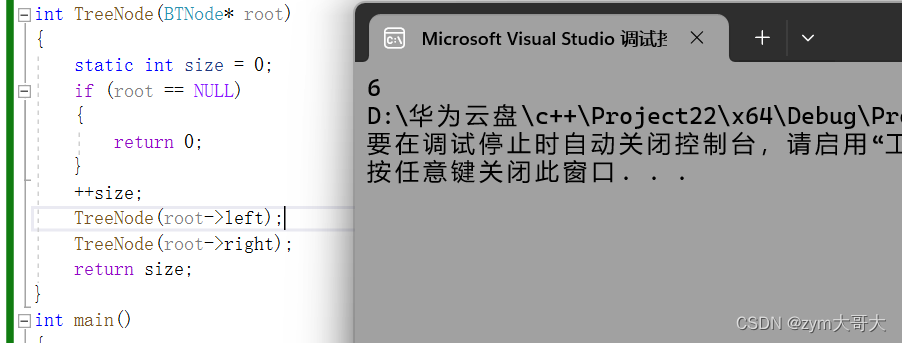
int TreeNode(BTNode* root)
{static int size = 0;if (root == NULL){return 0;}++size;TreeNode(root->left);TreeNode(root->right);return size;
}
多次調用計算函數:
會導致一直積累
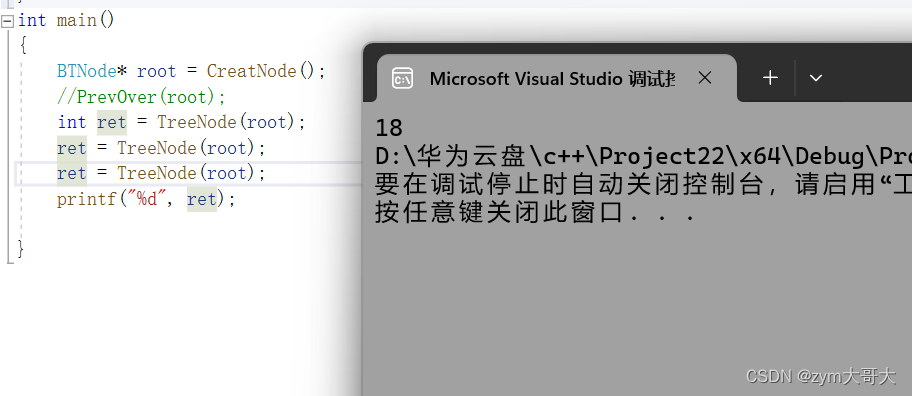 ?
?
錯誤代碼3:
int size = 0;
int TreeNode(BTNode* root)
{if (root == NULL){return 0;}++size;TreeNode(root->left);TreeNode(root->right);return size;
}只需要把size從局部變量變成全局變量就行,這樣遞歸過程中的每個函數的size都是同一個size了,全局變量的生命周期是程序結束,同static一樣,但是相對static的方法安全一些,使用static需要謹慎。
合理代碼:
int TreeNode(BTNode* root)
{return root == NULL ? 0 : TreeNode(root->left) + TreeNode(root->right) + 1;
}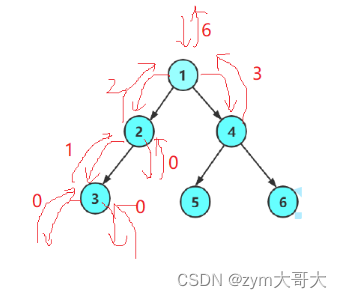
把根結點分成左子樹和右子樹在加1(計入一個結點數量),每次進入一個結點都會有左子樹和右子樹,每進入一個結點就計入1,直到root=NULL時返回0,就把關于根和子樹所計入的數返回到上一個結點去,通過這樣會一直返回到最上面的結點,就把所有結點的數量都計入進去了,不會出現多次調用函數而發生數量的變化。
2.3計算二叉樹的高度
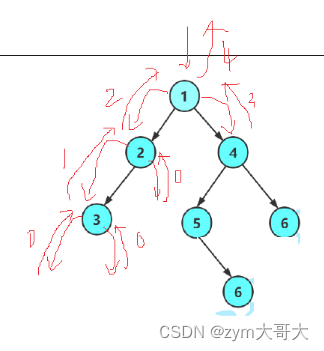
因為根結點有左右倆個子樹,樹的高度是由最長的決定的,所有要對比左右倆個子樹的長度,找到長度長的子樹,再加上一(根結點算一個高度),這樣就計算出樹的高度了。
錯誤代碼:
int TreeHeight(BTNode* root)
{if (root == NULL){return 0;}return TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left)+1 : TreeHeight(root->right)+1;
}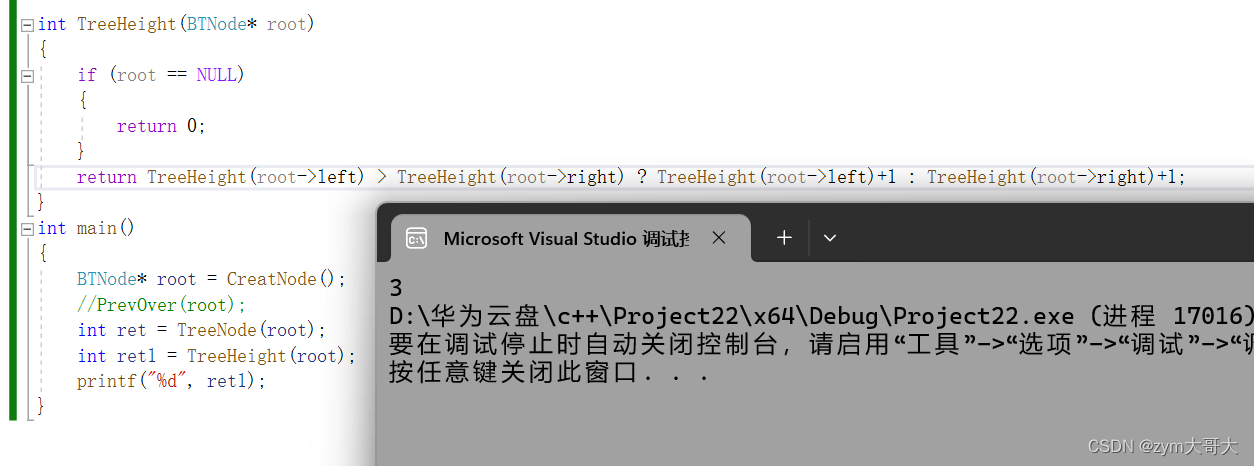
這樣雖然可以計算出樹的高度,但是存在一個問題,函數會在樹的最下面開始計入,比我后在返回值那里又要計算一次,因為這個是沒有變量來存儲計入的值,所有每次對比和返回值時都要在通過遞歸來得到計入的值,如果樹的高度是大的,那么當遞歸到較為上面時,在往下遞歸就會導致程序運行慢,一直重復計算,計算最底下的結點的度會因為結點的上走而暴增,倒數第二層計算最后一層結點的度會執行倆次,倒數第三層則會計算最后一層結點四次,所以這個代碼是不合適的。
改進代碼:
分析:
通過遞歸會找到最下面的結點,既葉子結點,開始往上走,返回的地方就是比較那邊大,就往那邊加一(這里的一是根的計入),直到走到最上面結點,這時比較就是總的左子樹和右子樹的高度(不是最上面結點)。
int TreeHeight(BTNode* root)
{if (root == NULL){return 0;}int heightleft = TreeHeight(root->left);int heightright = TreeHeight(root->right);return heightleft > heightright ? heightleft +1 : heightright +1;
}創建臨時變量來存儲函數返的值,就不用重復計算,可以提高運行速度,減少消耗。
2.4計算樹的葉子結點個數
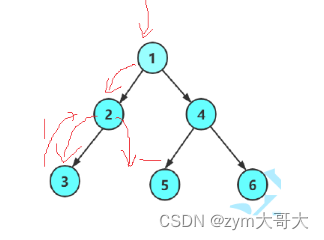
葉子結點的左右子數都是NULL,可以以此為特點找。
錯誤代碼:
int LeafNode(BTNode* root)
{if (root->left == NULL && root->right == NULL)return 1;return LeafNode(root->left) + LeafNode(root->right);
}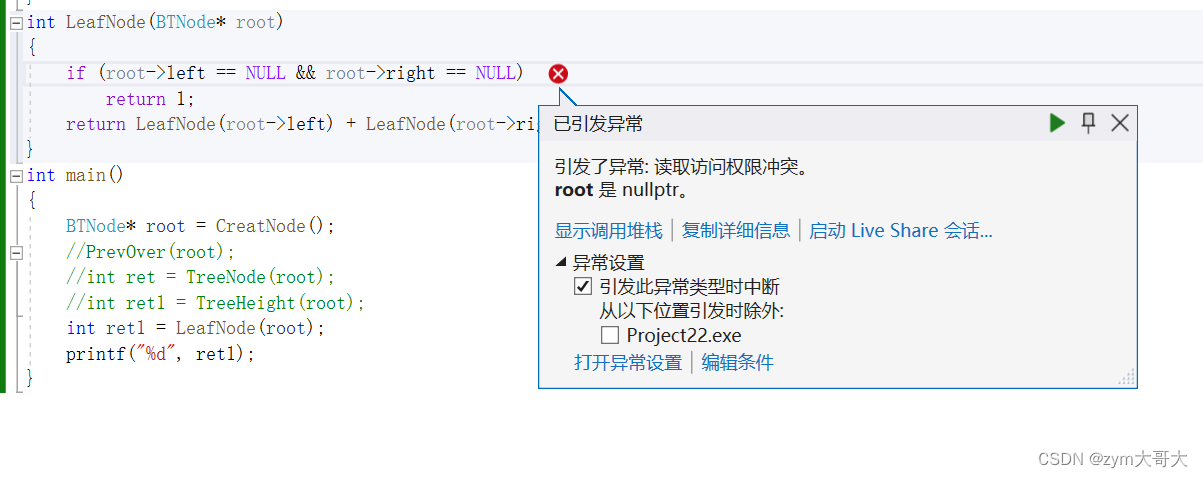
因為二叉樹不是所有結點都有左右子樹,有些子樹是NULL,如果為NULL則是不能用->符號引用的,所以代碼是不合理的。
改進代碼:
int LeafNode(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return LeafNode(root->left) + LeafNode(root->right);
}
先在最前面判斷是否為空,在進行下面的操作,就可以避免遇到NULL而去解引。
3.解決單值二叉樹題

?題意可以知道單值二叉樹是結點的值是一樣的,需要去遍歷二叉樹去判斷是否所有的值都相等,
通過判斷根和左右子樹是否相等,如果每個根和左右子樹都相等,則整體的全部值也會相等,就像a=b,b=c,所以a=b=c。
代碼:
bool isUnivalTree(struct TreeNode* root) {if(root==NULL)return true;if(root->left&&root->left->val!=root->val)return false;if(root->right&&root->right->val!=root->val)return false;return isUnivalTree(root->left)&&isUnivalTree(root->right);}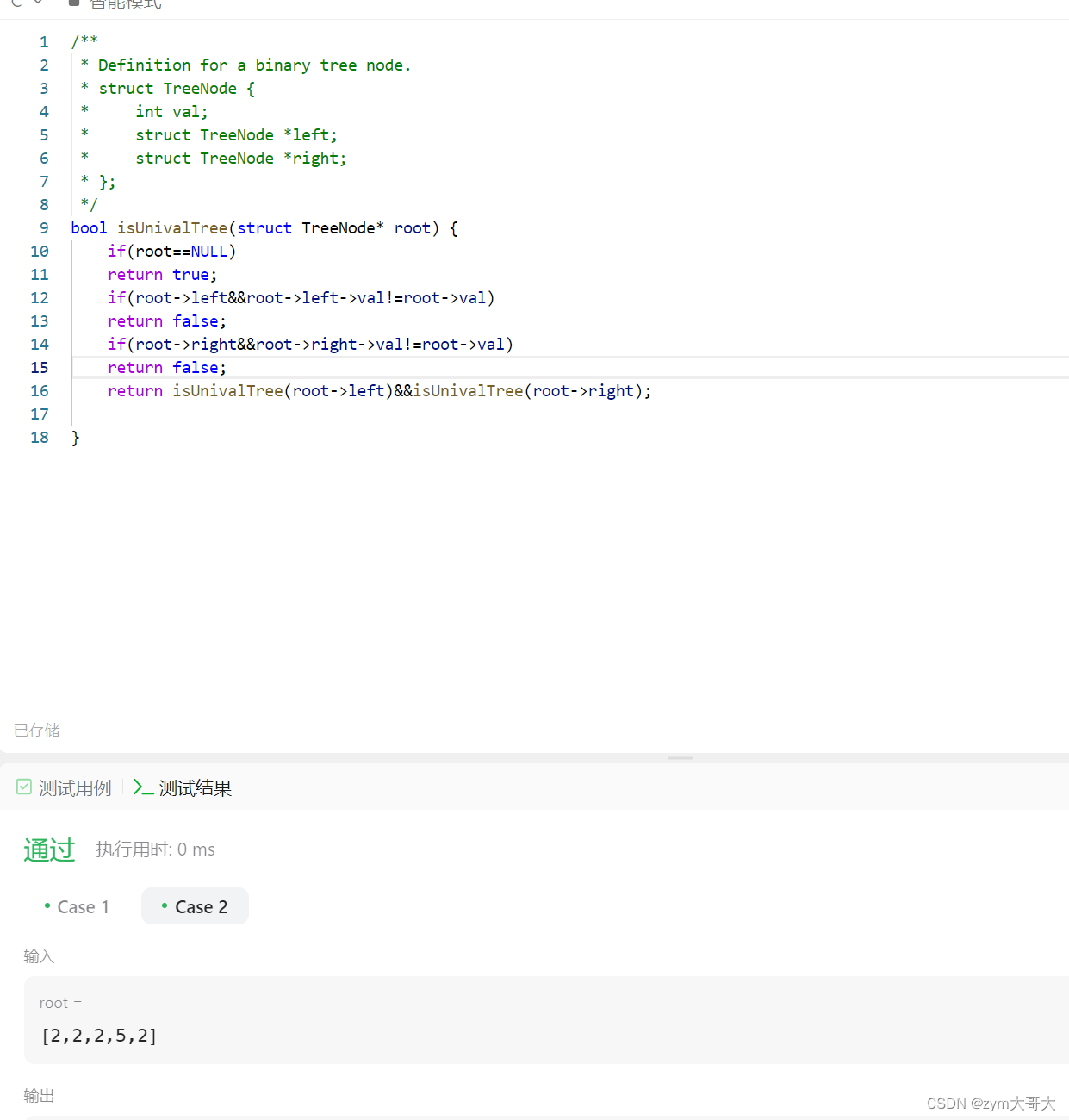
分析:
之所用如果不相等就返回false是因為后面的子結點是否相等還不知道,判斷相等就返回true太早了,可能后面的值與前面的不相等,只有全部相等才能返回true。?


文件夾)





)
總數算不出+隨機抽取10張)






)


