1.01矩陣

既然本章是BFS解決多源最短路問題,也就是說有若干個起點,那我們就可以暴力一點,直接把多源最短路徑問題轉化成若干個單源最短路徑問題,然后將每次的步數比較一下,取到最短的就是最短路徑的結果,這個想法好寫,但是在本章都會超時,所以我們換一個思路:把所有的源點當成一個超級源點(包含所有的源點),那么問題就變成了單一的單源最短路徑問題,此時我們使用一次bfs就可以解決問題。但是如何將這個源點當作一個超級源點呢?在解決單源最短路問題,我們的做法是把起點加入到隊列,然后一層一層的往外擴展,所以我們只需要一開始將所有的起點都加入到隊列,然后一層一層往外擴展即可,我們直接看第一個思路:
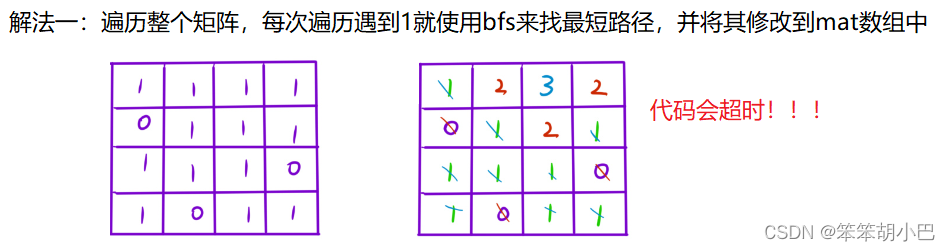
代碼我已經替大家試過了,會超時,所以我們來看第二種思路:

直接上代碼:
class Solution {int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};
public:vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {int m = mat.size();int n = mat[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));// dist[i][j] == -1,表示:沒有被搜索過// dist[i][j] != -1,表示:最短距離// 利用dist來直接標記該位置是否已經被使用queue<pair<int,int>> q;// 把所有為0的源點加入隊列中for(int i = 0; i < m; i++) for(int j = 0; j < n; j++)if(mat[i][j] == 0){q.push({i, j});dist[i][j] = 0;}while(q.size()){// 此時我們不需要同時向外擴展// 因此不需要使用szauto [a, b] = q.front();q.pop();for(int i = 0; i < 4; i++){int x = a + dx[i], y = b + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){// 此時說明已經找到,直接修改dist的值即可dist[x][y] = dist[a][b] + 1;q.push({x, y});}}}return dist;}
};2.飛地的數量

這道題目如果我們按照每次遍歷數組每次遇到1就去bfs,肯定是會超時的,但是根據這個寫法也有不超時的做法,我們遍歷的時候,遇到1就去bfs,并將途中遇到1的位置標記一下,下一輪遇到1的時候,先dfs一下,如果這次dfs寬搜的時候遇到1,發現這個位置已經標記過,此時就不要bfs了,直接就是上次的結果,但是這樣寫需要兩次dfs,并且dsf的代碼還不一樣,也比較麻煩,那我們來一個新思路:正難則反,我們可以從邊上的 1 開始搜索,把與邊上 1 相連的聯通區域全部標記?下; 然后再遍歷?遍矩陣,看看哪些位置的 1 沒有被標記即可標記的時候,可以用「多源 bfs 」解決,bfs的邏輯和上一個題目基本差不多,直接上代碼。
class Solution {int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};bool vis[501][501] = {false};
public:int numEnclaves(vector<vector<int>>& grid) {int m = grid.size();int n = grid[0].size();// 1. 把邊上的 1 加?到隊列中queue<pair<int,int>> q;// 遍歷行for(int i = 0; i < n; i++){if(grid[0][i] == 1)q.push({0, i});if(grid[m - 1][i] == 1)q.push({m - 1, i});}// 遍歷列for(int j = 0; j < m; j++){if(grid[j][0] == 1)q.push({j, 0});if(grid[j][n - 1] == 1)q.push({j, n - 1});}// 2. 多源bfswhile(q.size()){auto [a, b] = q.front();q.pop();vis[a][b] = true;for(int i = 0; i < 4; i++){int x = a + dx[i];int y = b + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && !vis[x][y]){q.push({x, y});vis[x][y] = true;}}}// 統計結果int ret = 0;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(grid[i][j] == 1 && !vis[i][j])ret++;return ret; }
};3.地圖中的最高點
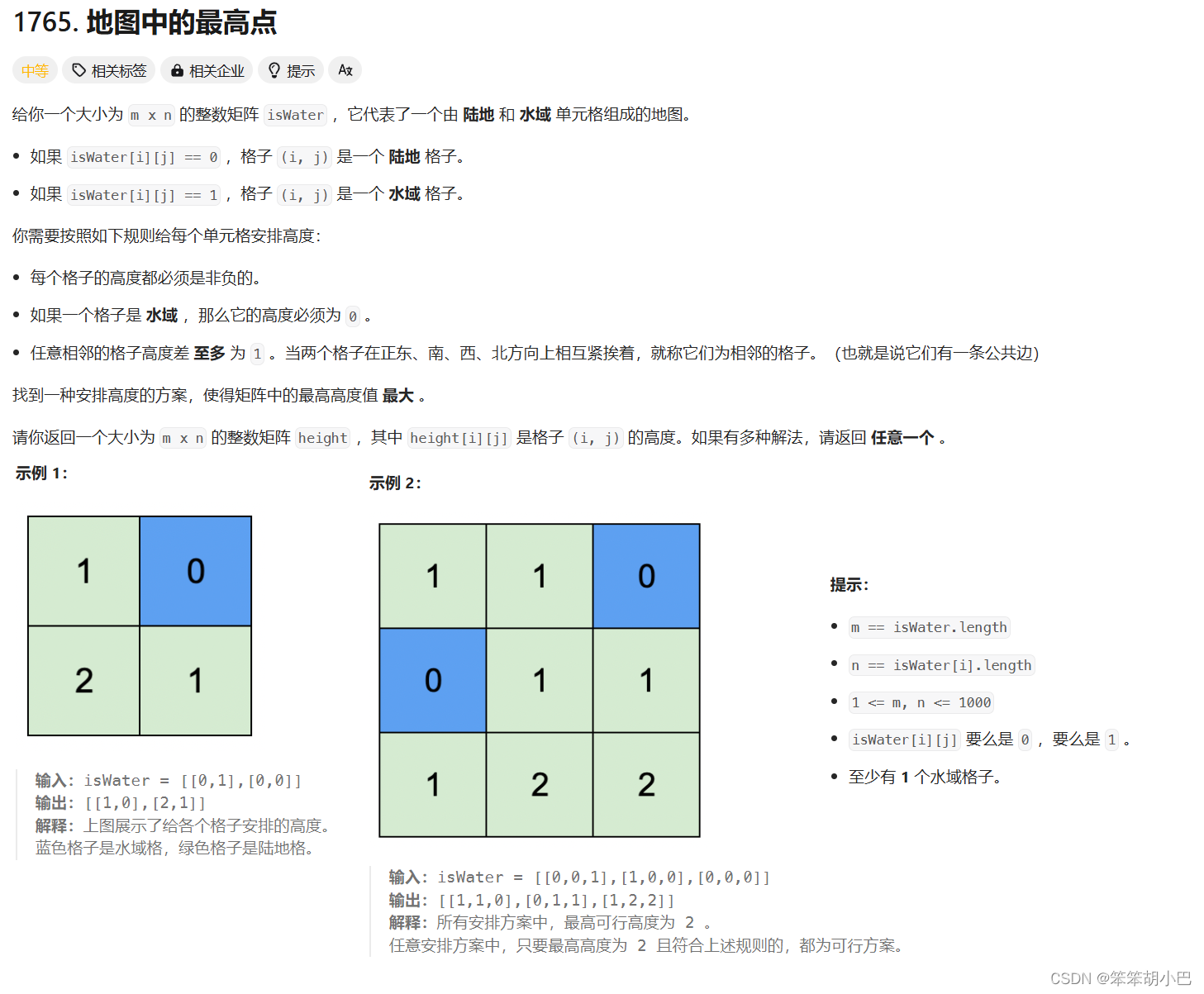
注意本題給的是結果矩陣,我們可以先來看看原始矩陣的樣子
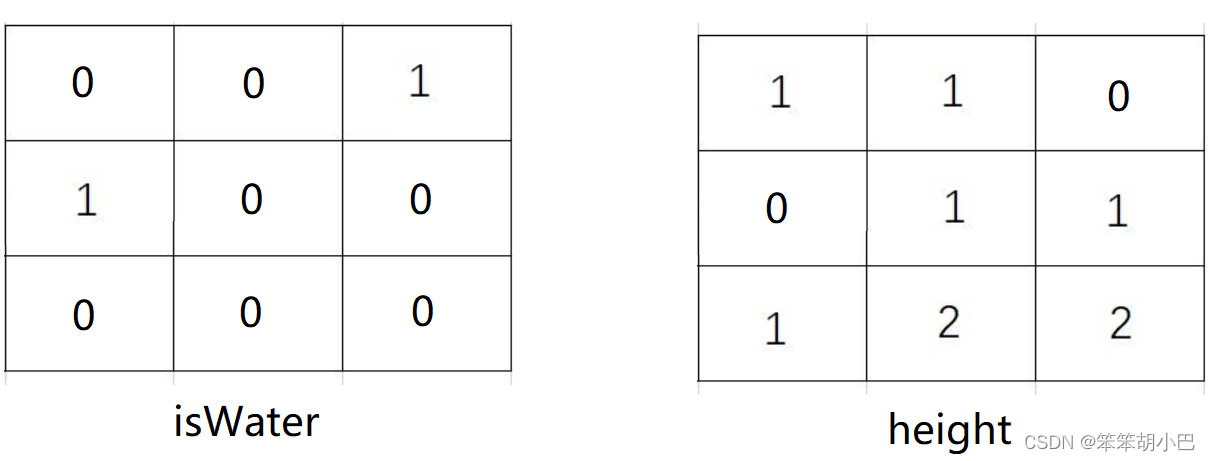
此時就一目了然了,我們直接創建一個height數組,將isWater中的水域依次向外擴展,直接轉化成多源bfs的問題,并且我們發現它就是01矩陣的變型題,直接上代碼了:
class Solution {int dx[4] = { 0, 0, 1, -1 };int dy[4] = { 1, -1, 0, 0 };
public:vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {int m = isWater.size();int n = isWater[0].size();// 數組不能初始化為0,因為數組中存在0 - 代表水域vector<vector<int>> height(m, vector<int>(n, -1));queue<pair<int, int>> q;// 把所有的源點加入到隊列里面for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)if (isWater[i][j] == 1){height[i][j] = 0;q.push({ i,j });}// 多源bfswhile (q.size()){auto [a, b] = q.front();q.pop();for (int i = 0; i < 4; i++){int x = a + dx[i];int y = b + dy[i];// 該值沒有被搜索過if (x >= 0 && x < m && y >= 0 && y < n && height[x][y] == -1){height[x][y] = height[a][b] + 1;q.push({ x, y });}}}return height;}
};4.地圖分析

我們這個題目要求解海洋到陸地的最大距離,也可以求,但是海洋數量多蠻煩,正難則反,我們可以求陸地到海洋,將陸地作為超級源點依次向外擴展,隨后創建一個dist數組,記錄每次bfs的值保存在ist數組中即可解決,代碼和上面的題目都相似,直接上代碼:
class Solution
{int dx[4] = { 0, 0, 1, -1 };int dy[4] = { 1, -1, 0, 0 };
public:int maxDistance(vector<vector<int>>& grid){int m = grid.size(), n = grid[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));queue<pair<int, int>> q;for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)if (grid[i][j] == 1){dist[i][j] = 0;q.push({ i, j });}int ret = -1;while (q.size()){auto [a, b] = q.front(); q.pop();for (int i = 0; i < 4; i++){int x = a + dx[i], y = b + dy[i];if (x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){dist[x][y] = dist[a][b] + 1;q.push({ x, y });ret = max(ret, dist[x][y]);}}}return ret;}
};
)





 —— 基礎概念(0))

:學習框架)

)


—集成炫酷的粒子特效)




