一、二叉樹結尾
1、如何判斷一棵樹是完全二叉樹。
我們可以使用層序遍歷的思路,利用一個隊列,去完成層序遍歷,但是這里會有些許的不同,我們需要讓空也進隊列。如果隊列里到最后只剩下空那么這棵樹就是完全二叉樹。具體的實現如下:
借助了,按層序走,非空節點一定是連續的。
int TreeComplete(BTNode* root)
{assert(root);Queue q;QueueInit(&q);QueuePush(&q,root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)break;QueuePush(&q, front->left);QueuePush(&q, front->right);}//判斷是不是完全二叉樹//后面非空,說明非空節點不是連續的,不是完全二叉樹while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front)return false;}QueueDestory(&q);return true;
}二叉樹的銷毀
使用后序去銷毀
void TreeDestory(BTNode* root)
{if (root == NULL)return;TreeDestory(root->left);TreeDestory(root->right);free(root);
}二、排序
1、插入排序。
把一個數據插入到有序的區間,定義一個end變量用來標識區間
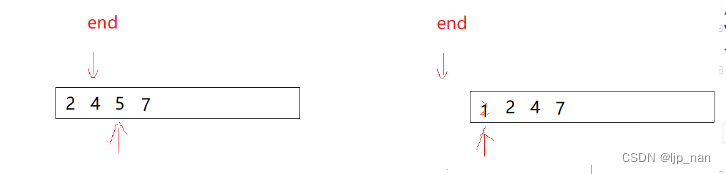
void InsertSort(int* a, int n)
{for (int i = 1; i < n; i++){//單躺排序int temp = a[i];int end = i - 1; while (end >= 0){if (temp < a[end]){a[end + 1] = a[end];end--;}else{//為什么要break,這里會有end為-1的位置break;}}a[end + 1] = temp;}
}
?2、希爾排序
(1)預排序--目標:數組接近有序,分組插入排序,間隔為gap分為一組,對每組數據插入排序,假設gap == 3;
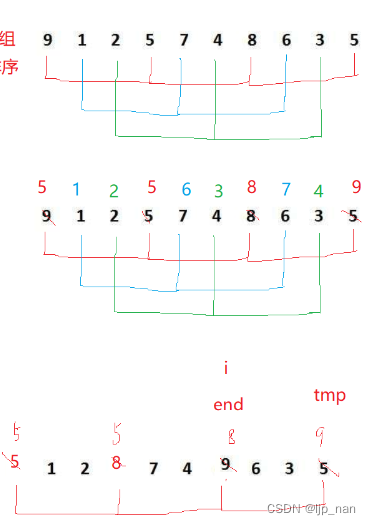
gap為3時的一趟直接插入排序
int end;int gap = 3;int temp = a[end+gap];while (end >= 0){if (temp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;} }a[end + gap] = temp;gap為3時的紅色組數據的排序
void ShellSort(int* a, int n)
{int gap = 3;for (int i = gap; i < n; i += gap){int end = i - gap;int temp = a[end + gap];while (end >= 0){if (temp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = temp;}}三組都排完
void ShellSort(int* a, int n)
{int gap = 3;for (int j = 0; j < gap; j++){for (int i = gap + j; i < n; i += gap){int end = i - gap;int temp = a[end + gap];while (end >= 0){if (temp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = temp;}}
}把上述代碼改成i++可以減少一層循環,就變成了多組并排的方式
gap到底時多少合適呢?
gap越大,跳的越快,越不接近有序
gap越小,跳的越慢,越接近有序?
gap = gap/1
gap = gap/3 + 1
//希爾排序
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 2;for (int j = 0; j < gap; j++){for (int i = gap + j; i < n; i += gap){int end = i - gap;int temp = a[end + gap];while (end >= 0){if (temp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = temp;}}}
}
(2)直接插入排序
gap為1的時候為直接插入排序
gap >1的時候為預排序
時間復雜度O(n^1.3)左右的樣子
3、選擇排序
我們可以找到最大的交換到右邊和最小的交換到左邊,但是如果left == maxi,一交換mini和left的值就會把maxi里的值交換到mini上。我們需要做一個修正,maxi = mini
void Swap(int* a, int* b)
{int temp = *a;*a = *b;*b = temp;
}
void SelectSort(int* a, int n)
{//首先進行選數int left = 0;int right = n - 1;while (left < right){int maxi = left, mini = left;for (int i = left; i <= right; i++){if (a[i] < a[mini])mini = i;if (a[i] > a[maxi])maxi = i;}//選數完畢交換兩個數Swap(&a[mini], &a[left]);//進行矯正if (left == maxi)maxi = mini;Swap(&a[maxi], &a[right]);left++;right--;}
}選擇排序最壞和最好的時間復雜度為O(n^2)
4、堆排序已經在二叉樹堆已經講過了
5、冒泡排序
void BubbleSort(int* a, int n)
{for (int i = 0; i < n; i++){for (int j = 0; j < n - i; j++){if(a[j] > a[j+1])Swap(&a[j], &a[j + 1]);}}
}優化:
void BubbleSort(int* a, int n)
{for (int i = 0; i < n; i++){bool exchange = false;for (int j = 0; j < n - i; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);//沒有改成true證明已經有序了exchange = true;}}if (exchange == false)break;}
}部分有序時插入排序和冒泡排序就是有差距的。
6、快速排序
選出一個關鍵值key,把它放到正確的位置(最終排好序要在的位置)單趟排序
左邊放比key小的,右邊放比key大的
HOARE版本
左邊做key,右邊先走(相遇后,相遇位置正好是小的),右邊找比key小的。左邊找比key大的,然后交換

快排是一個遞歸的思想,分成左右區間,然后再排
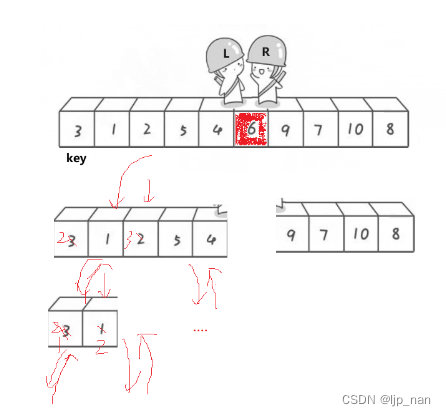
? ? ? ? ?begin? = 0? ? keyi = end? ?
? ? ? ? end = 1? ? ? ? keyi + 1 = 2?? end = 1? ? 左大于等于右不存在這個區間? (遞歸的出口)
void QuickSort(int* a, int left,int right)
{if (left >= right){return;}int keyi = left;int begin = left, end = right;while (left < right){//相等的話沒有必要交換//不加前面的條件會越界訪問//一定先讓右先走//右邊找小while (left < right && a[right] >= a[keyi])right--;//左邊找大while(left < right && a[left] <= a[keyi])left++;Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;//[begin,keyi-1][keyi][keyi+1,end]QuickSort(a,begin, keyi - 1);QuickSort(a, keyi + 1, end);
}時間復雜度O(NlogN)

上面有一個錯誤應該是n-2^i+1
最壞的情況是逆序和順序的時候。它的時間復雜度就已經變到了O(N^2),可能會棧溢出。
優化
我們可以隨機選key也可以使用三數取中法選key
int GetMidNumi(int* a, int left, int right)
{int midi = (right + left) / 2;if (a[left] < a[midi]){if (a[midi] < a[right]){return midi;}else if (a[left] > a[right]){return left;}else{return right;}}else //a[left] > a[midi]{if (a[midi] > a[right]){return midi;}else if (a[left] < a[right]){return left;}else{return right;}}
}
void QuickSort(int* a, int left,int right)
{if (left >= right){return;}/*int randi = left + (rand() % (right - left));Swap(&a[left], &a[randi]);*///三數取中找到下標//int keyi = left;int midi = GetMidNumi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;int begin = left, end = right;while (left < right){//相等的話沒有必要交換//不加前面的條件會越界訪問//一定先讓右先走//右邊找小while (left < right && a[right] >= a[keyi])right--;//左邊找大while(left < right && a[left] <= a[keyi])left++;Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;//[begin,keyi-1][keyi][keyi+1,end]QuickSort(a,begin, keyi - 1);QuickSort(a, keyi + 1, end);
}那么為什么相遇的位置一定比key小
左邊做key,右邊先走,保證相遇位置比key要小
1、R找小,L找大沒有找到,L遇到R或者就是key的位置
2、R找小找不到,R直接跟L相遇,要么就是一個比key小的位置,或者直接到keyi
類似的道理右邊做key左邊先走也是這樣的。相遇的位置比key要大
挖坑法
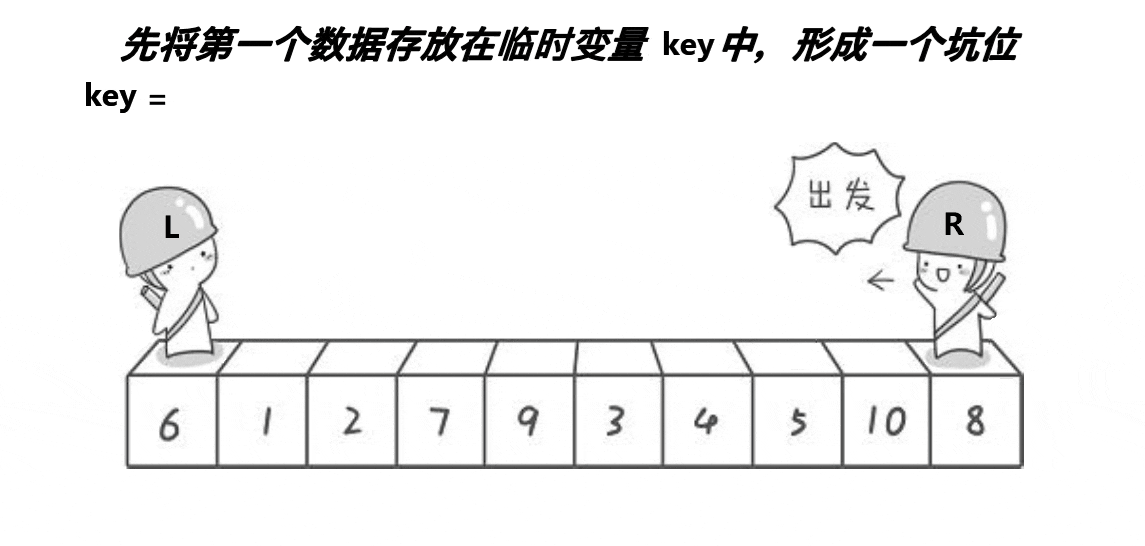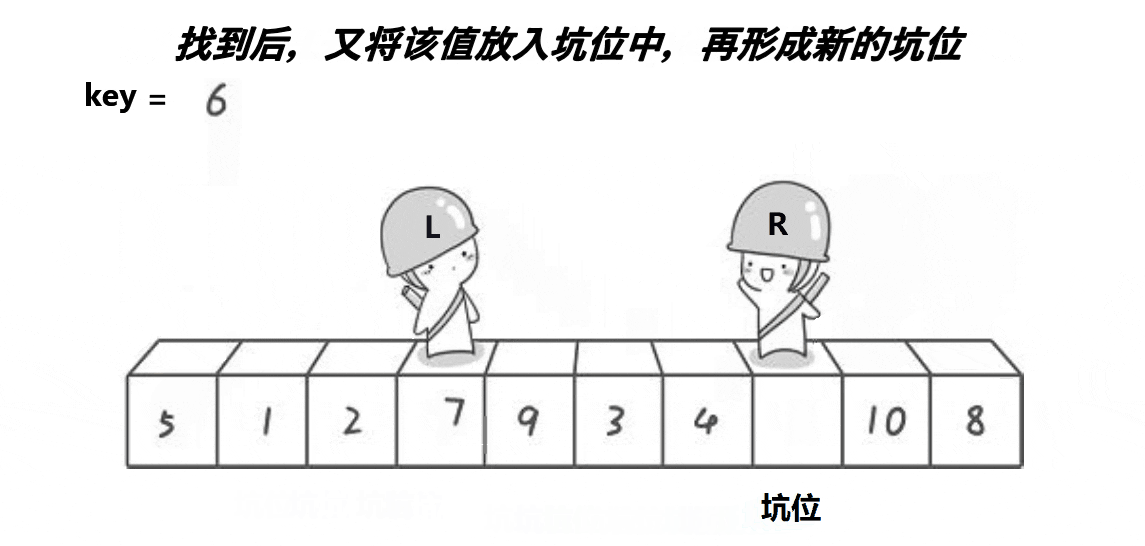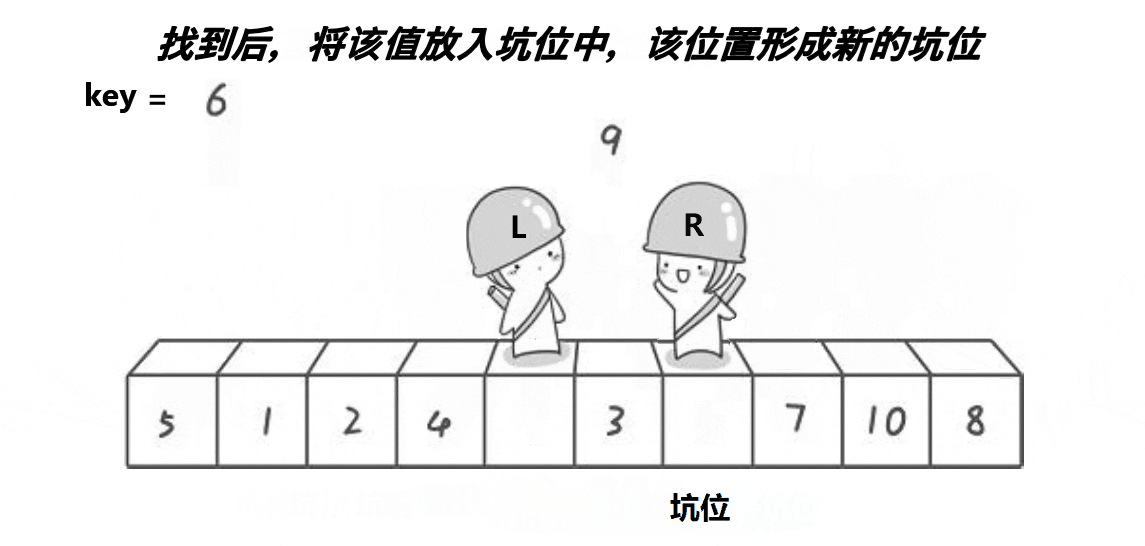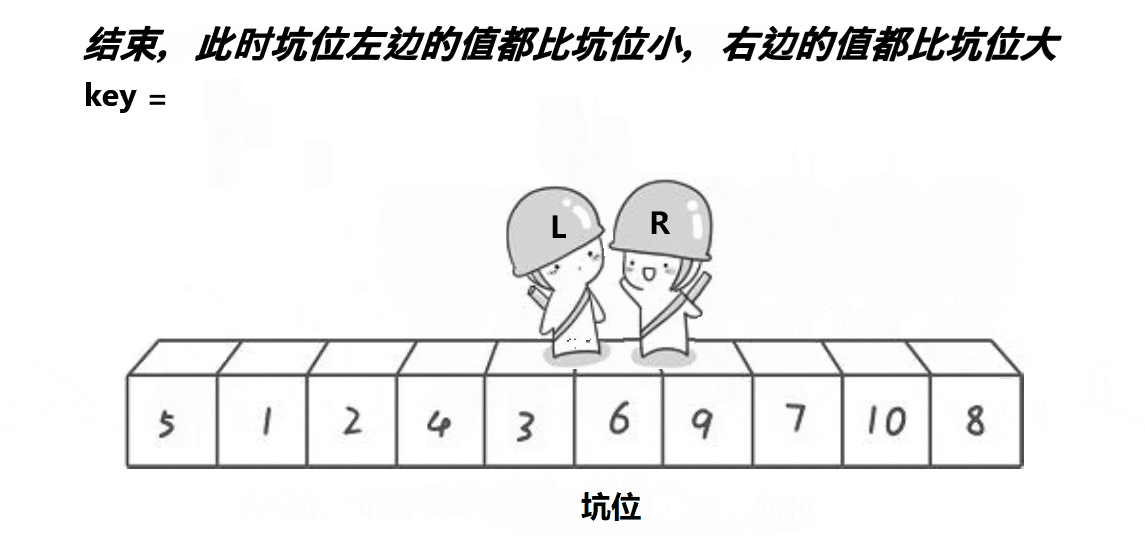
?
void QuickSort2(int* a, int left, int right)
{if (left >= right){return;}/*int randi = left + (rand() % (right - left));Swap(&a[left], &a[randi]);*///三數取中找到下標//int keyi = left;int midi = GetMidNumi(a, left, right);Swap(&a[left], &a[midi]);int begin = left, end = right;int key = a[left];int hole = left;while (left < right){//相等的話沒有必要交換//不加前面的條件會越界訪問//一定先讓右先走//右邊找小while (left < right && a[right] >= key)right--;//找到以后把值放到left上面a[hole] = a[right]; //形成新的坑位hole = right;//左邊找大while (left < right && a[left] <= key)left++;//找到后把值放到right上面a[hole] = a[left]; //形成新的坑位hole = left;}a[hole] = key;//[begin,keyi-1][keyi][keyi+1,end]QuickSort(a, begin, hole - 1);QuickSort(a, hole + 1, end);
}雙指針法
1、cur找到比key小的值++prev,cur和prev位置的值交換,++cur
2、cur找到比key大的值,++cur
說明:prev要么緊跟著cur(prev下一個就是cur)
prev跟cur中間間隔著比key大的一段值的區間。
把比key大的值往右翻,比key小的值,翻到左邊。
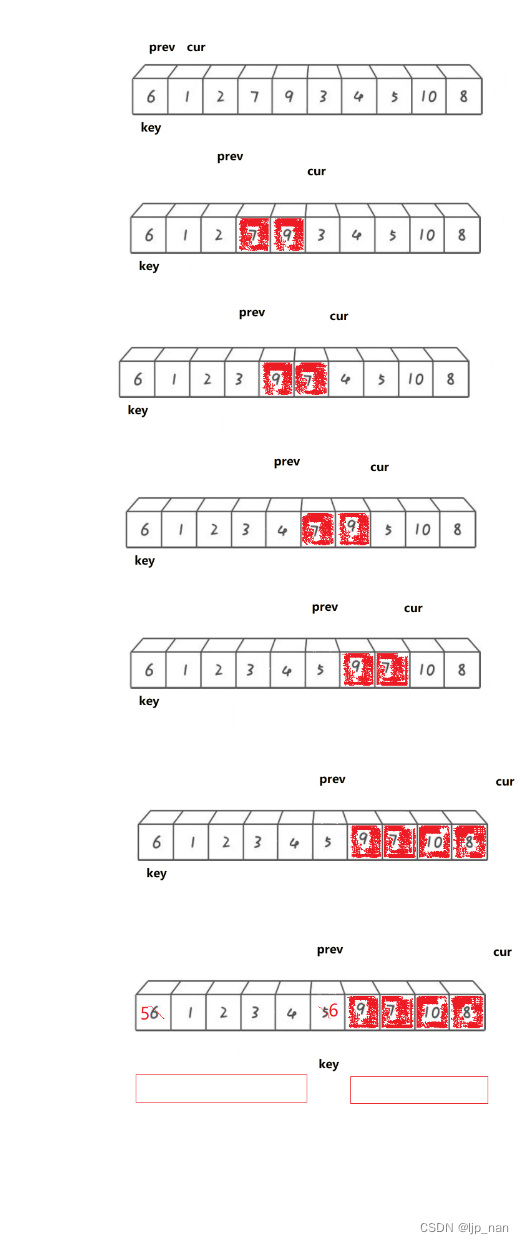
void QuickSort3(int* a, int left, int right)
{if (left >= right)return;int midi = GetMidNumi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;int cur = left + 1;int prev = left;while (cur <= right){//cur找到比key小的值,++prev,然后交交換兩個位置的值,cur++//cur找到比key大的值,++curif (a[keyi] > a[cur]&&++prev != cur)Swap(&a[prev], &a[cur]);cur++;}Swap(&a[prev], &a[keyi]);keyi = prev;QuickSort3(a, left, keyi-1);QuickSort3(a, keyi + 1, right);
}
小區間優化
到了遞歸的最后三層的時候,我們可以使用直接插入排序來排序,這樣我們會減少百分之87.5的遞歸。這樣的優化為小區間優化。小區間直接插入排序
void QuickSort3(int* a, int left, int right)
{if (left >= right)return;//加上小區間優化if ((right - left + 1) > 10){int keyi = PartSort3(a, left, right);QuickSort3(a, left, keyi - 1);QuickSort3(a, keyi + 1, right);}else{InsertSort(a + left, right - left + 1);}
}
快排的非遞歸
遞歸的問題
效率,深度太深,會棧溢出。
遞歸改非遞歸
直接改成循環
使用棧輔助改循環?
如何改非遞歸,遞歸棧幀里面放的是區間。區間在變化,所以我們可以在棧里面存區間。最開始存0 - 9,進行單趟排,左區間是0 4,有區間是[ 6 ,9] 可以把這兩個區間入棧,每次入棧如此反復。先入右區間,再入左區間。
1、棧里面取一段區間,單趟排序
2、單趟分割子區間入棧
3、子區間只有一個值或者不存在就不入棧
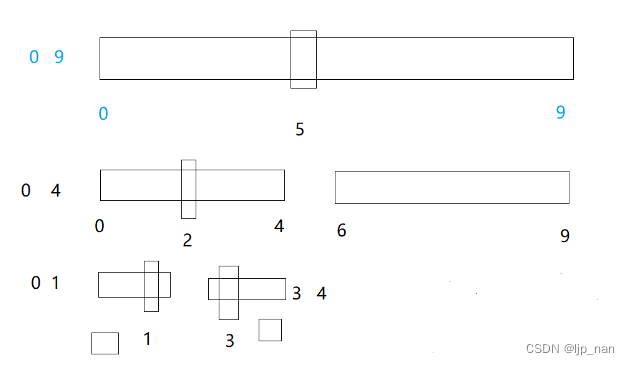
//實質就是利用自己實現的棧,來模擬編譯器中的棧幀
void QuickSortNonR(int* a, int left, int right)
{ST st;STInit(&st);//先讓0-9區間入棧STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)){//第二步,出棧,得到區間int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);//取出區間后進行一趟排序int keyi = PartSort3(a, begin, end);//然后劃分出區間//[begin,keyi-1][keyi][keyi+1,end]if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi + 1);}if (begin < keyi - 1){STPush(&st, keyi - 1);STPush(&st, begin);}}STDestory(&st);
}7、歸并排序
兩個有序區間歸并:依次比較,小的尾插到新空間。
但是不滿足有序區間呢。我們可以使用分治的思想,使左右區間有序。相當于二叉樹的后續遍歷,先分區間,再歸并。時間復雜度為O(NlogN)。
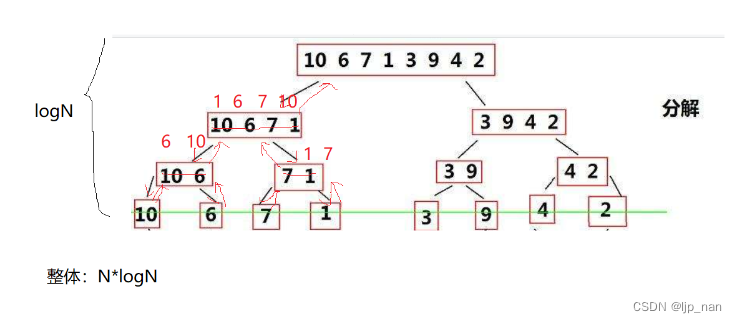
開一個臨時數組,歸并到臨時數組,完了以后再拷貝回去。遞歸左區間再遞歸右區間
左右有序,再歸并
void _MergeSort(int* a, int left, int right, int* temp)
{//遞歸返回條件if (left >= right){return;}//首先劃分區間int mid = (right + left) / 2;//然后使左右區間有序,采用分治的思想//[left,mid][mid + 1,right]_MergeSort(a, left, mid, temp);_MergeSort(a, mid + 1, right, temp);//接下來進行歸并int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;//誰小就尾插進去int i = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){temp[i++] = a[begin1++];}else{temp[i++] = a[begin2++];}}while (begin1 <= end1){temp[i++] = a[begin1++];}while (begin2 <= end2){temp[i++] = a[begin2++];}//歸并完成進行拷貝memcpy(a + left, temp + left, sizeof(int) * (right - left + 1));
}
void MergeSort(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc");return;}_MergeSort(a, 0, n - 1, temp);free(temp);
}歸并排序的非遞歸可以使用循環來實現,思路是

但是這個方法的邊界處理有點麻煩
gap是歸并過程中每組的個數,邊界的控制
第一組:[i, i+gap-1]
第二組:[i + gap,i+2*gap-1]
那么如果遇到是奇數個可能會導致越界訪問。
1、end1越界了怎么辦? 不歸并了

?2、end1沒有越界 begin2越界了,跟1一樣處理
?3、end2越界了,前面的都沒有越界,修正end2到n-1
void MergeSortNonR(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc");return;}int gap = 1;//接下來進行歸并while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//誰小就尾插進去//如果是奇數個怎么辦,我們可以分類討論進行修正if (end1 >= n || begin2 >= n){break;}else if (end2 >= n){end2 = n - 1;}int j = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){temp[j++] = a[begin1++];}else{temp[j++] = a[begin2++];}}while (begin1 <= end1){temp[j++] = a[begin1++];}while (begin2 <= end2){temp[j++] = a[begin2++];}//歸并完成進行拷貝memcpy(a + i, temp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}free(temp);
}?上面的排序除了歸并排序外,都是內排序,也就是在內存中排序。歸并排序內外都可以。
非比較排序:
1、計數排序
統計每個數據出現的個數
進行排序

總結:

void CountSort(int* a,int n)
{//先求出范圍int max = a[0], min = a[0];for (int i = 0; i < n; i++){if (a[i] > max)max = a[i];if (a[i] < min)min = a[i];}int range = max - min + 1;//求出每個數出現的次數int* countA = (int*)malloc(sizeof(int) * range);memset(countA, 0, sizeof(int) * range);for (int i = 0; i < n; i++){countA[a[i] - min]++;}//進行排序int j = 0;for (int i = 0; i < range; i++){while (countA[i]--){a[j++] = i + min;}}free(countA);
}2、基數排序
3、桶排序
上面的排序基本上不會用到,這里就不在描述
時間復雜度總結
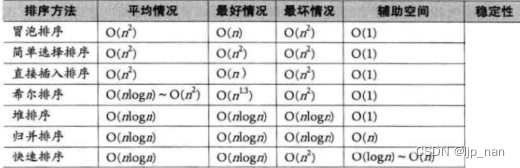
穩定性:相同數據的相對順序是否穩定,注意是相等的數談穩定性
穩定:冒泡排序,插入排序,歸并排序。
不穩定:選擇排序,希爾排序,堆排序,快速排序。














-掌握屏幕單位,應對千變萬化的設備)




