一、CT到底測了什么?
硬件動作
X 射線源與探測器陣列對置,圍著物體旋轉。
每轉到一個角度 θ(也叫一個視角 / view),源發射扇形/平行的射線束,探測器陣列上有很多“通道/像素/bin”(記作索引 n)。
每個探測器通道在該角度接收一條射線穿過物體后的強度
。
衰減物理(Beer–Lambert)
沿射線路徑,物體的線性衰減系數為
。理想單色下:
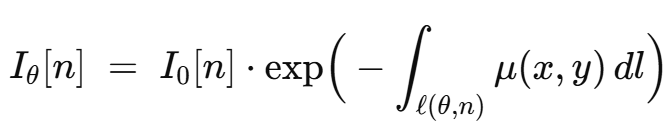
這一個標量 就是一條射線對物體的線積分(也稱射線和 / ray sum)。
結論:一個角度的一個探測器通道 = 一條射線 = 一個測量值 pθ[n]。
![]()
CT 單色理想模型里,探測器在角度 θ、通道位置 s 測到的對數強度,正是把待求的衰減系數 μ(x,y)在直線 L(θ,s) 上的積分。也就是說:
![]()
正弦圖 = Radon 變換的離散采樣。
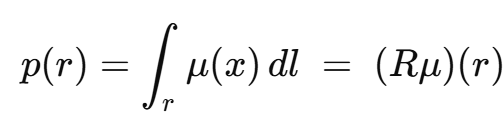
這里的 RRR(Radon 變換)是線性算子:對任意常數 a,b:
![]()
“CT 是線性的”指的就是:測量 ppp 與未知圖像 μ 的關系是線性的線積分關系,因此可用 FBP 這類線性逆重建。
二、把所有測量排成“正弦圖(sinogram)”
固定角度 θ,把該角度下所有通道 n=1…Ns 的
放成一行,叫一條投影。
旋轉到下一個角度
?,得到下一行。
堆疊所有角度 k=1…Nθ,得到一個二維數組:
![]()
這個二維數組就是正弦圖。
直覺:圖像中的一個點 (x0,y0)在正弦圖里會沿角度畫出一條正弦曲線,因此得名“sinogram”。
小例子:如果你有 600 個視角 × 641 個探測器通道,那正弦圖就是一個 600×641的二維矩陣。
三、從正弦圖回到圖像:Radon 變換與 FBP
數學上,μ(x,y) 經Radon 變換 R 變成 p(θ,s)(連續版,s 是探測器橫向坐標)。
我們手里有的就是它的離散采樣 P[k,n]。
重建就是求“逆 Radon 變換”。最經典的解析法是 FBP(Filtered BackProjection,濾波反投影):
濾波:對每個角度的投影在探測器方向做 1D 濾波(斜坡濾波 + 窗函數),補償模糊;
反投影:把每個角度、每個通道的濾波后數值,按幾何關系“抹回去”加到圖像像素上,所有角度累加,得到
。
Radon 變換把“圖像”映成“所有直線上的積分”;在 CT 里這就是“每條射線的對數測量”。拿到它(正弦圖)后,用 FBP 等逆方法就能把線積分“還原”為衰減系數圖像。
FBP = “按 Radon 反演公式實現”的工程算法:先濾波補償頻譜,再反投影還原圖像。
四、流程一圖流(2D 切片情形)
角度 θ1: Iθ1[n] → -ln(Iθ1[n]/I0[n]) → pθ1[n] → 作為正弦圖第1行
角度 θ2: Iθ2[n] → -ln(Iθ2[n]/I0[n]) → pθ2[n] → 作為正弦圖第2行...
角度 θK: IθK[n] → -ln(IθK[n]/I0[n]) → pθK[n] → 作為正弦圖第K行↓P[k,n](sinogram)↓FBP(每行先濾波,再把所有角度反投影求和)↓μ?(x,y)(重建圖像)
CT 就是:機器在很多角度上,用很多條射線穿過物體,探測器測到每條射線的強度 I;用同通道的空氣強度 I0 歸一化后做 ?ln?(I/I0),得到每條射線對衰減圖的線積分;把所有角度與通道排成正弦圖,再用 FBP/迭代法做逆 Radon 變換,重建出 μ(x,y)也就是斷層重建的圖像。






)












?)