【 C/C++ 算法】入門動態規劃-----一維動態規劃基礎（以練代學式）

每日激勵：“不設限和自我肯定的心態：I can do all things。 — Stephen Curry”

緒論?：
本章是動態規劃算法的基礎入門篇，我將通過三道簡單題 + 一道中等難度的一維動態規劃題來帶你對動態規劃有個初認識，并基本了解動態規劃的最基本常見的寫法，只有將基本寫法了解了，對后續的難的題目自然也不會毫無頭緒，后續還將持續更新更多相關的動規算法，敬請期待~🙃
————————
早關注不迷路，話不多說安全帶系好，發車啦（建議電腦觀看）。

👻動態規劃🌥?

這里通過大量練習得出下面動態規劃做題步驟
簡單的說動態規劃理解成：某種狀態的公式 + 提前求出來值的容器 求出當前位置的值然后放到容器中后后續使用
因為最開始的值一般是會看見的所以就能有初始值，從而啟動動態規劃

從上中可以主要提煉出：

狀態
容器的重要性
公式，可以換種說法：狀態轉移方程

這樣嚴格😈的說：動態規劃 = 狀態定義 + 狀態轉移方程 + 初始條件 + 狀態存儲（容器）

下述步驟是通過寫完下述四道題后的總結，所以同樣需要道友🗡?大量的練習沉淀最終就能對動態規劃的題目有一個基本的了解和思路，同時建議這里先一眼看過在做題中不斷的磨煉同時再看這里，慢慢的找感覺。

動規基本步驟

狀態表示：就是dp表（容器一般是數組）中里面的dp[ i ]值的含義
1. 通過經驗 + 題目要求：通常為：以 i 位置結尾，xxxxx
2. 分析問題的過程中，發現相同的子問題
狀態轉移方程：本質就是 dp[ i ] = ?（也是最難的一步）
1. 通過狀態表示再結合題目含義推導處dp[ i ]的值到底為多少
初始化：
1. 保證填表的時候不越界
2. 主要也是根據題目進行
填表順序：
1. 為了保證填寫當前狀態的時候前面狀態已經存到容器中，這樣才能進行計算
2. 一般是從左向右/從上到下
返回值
1. 通過最終得到的dp表和題意找到dp表中的結果

附???：

狀態表示：通常為：以 i 位置結尾/開頭，xxxxx
dp[ i ] 通常通過最后一個狀態來進行分析
初始化通常通過第一個狀態來進行分析
再做類似數字判斷時，不要使用字符來簡單的判斷，而是將數字字符根據位數轉變為真正的數字然后再進行判斷，不要偷懶會容易出現不可控的情況（具體見題目4）
適當的需要的情況下可以開辟空間來處理邊界問題，這點在后面稍微進階一點的動規來說就是使用的更多

🥴話不多說，從題目來以練代學式的快速上手，我也會邊分析過程邊使用上述的5步驟

具體訓練：

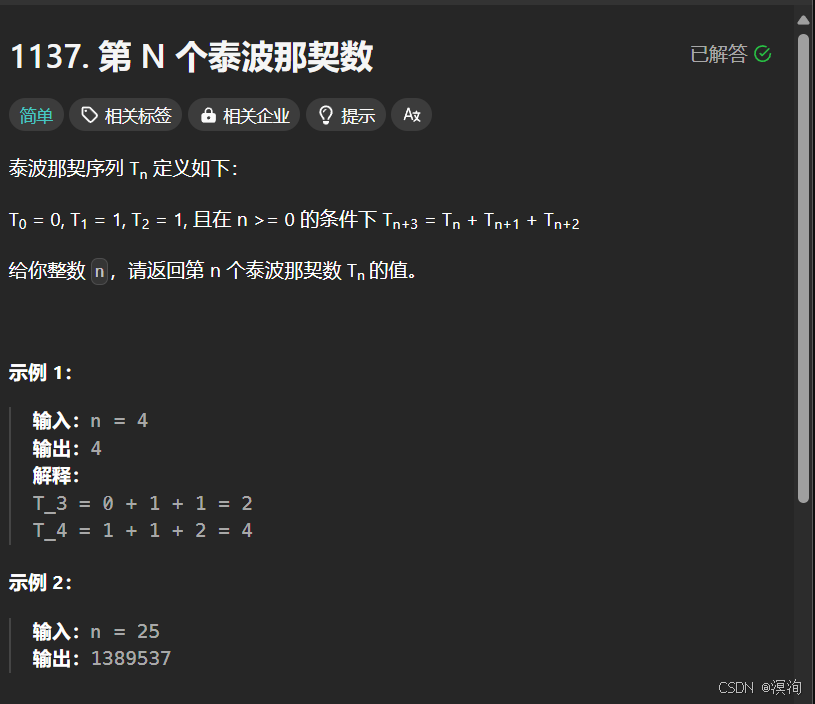
1. 第 N 個泰波那契數🤓

題目🍪：

在這里插入圖片描述

分析題目并提出，解決方法📕：

在這里插入圖片描述

回顧五大步驟：

狀態表示：就是dp表中里面的值的含義

怎么來：

經驗 + 題目要求
分析問題的過程中，發現子問題

狀態轉移方程：本質就是dp[ i ] 等于什么（也是最難的一步）
1. 根據狀態表示 + 題目含義得出
初始化
1. 保證填表的時候不越界
2. 也是根據題目意思進行填寫
填表順序
1. 為了填寫當前狀態的時候，所需要的狀態已經計算過了
2. 一般是從左向右/從上到下
返回值
1. 題目要求 + 狀態表示

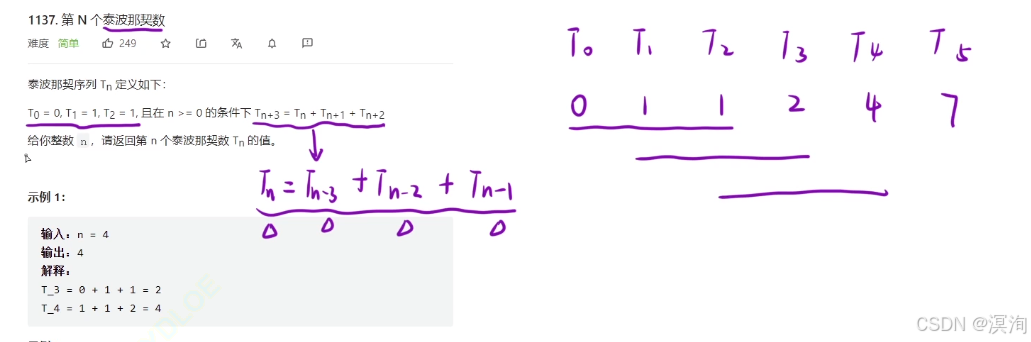
題解核心邏輯??：

狀態表述：dp[ i ]：第 i 個泰波那契數
1. 根據經驗 + 題目要求
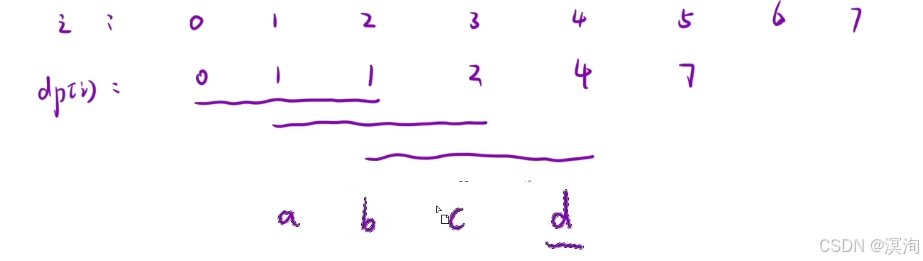
本題的轉移方程： dp[ i ] = dp[ i - 1 ] + dp[ i - 2 ] + dp[ i - 3 ]（通過上圖總的公式直接得出）
初始化，對本題的 dp[0]、dp[1]、dp[2] 這三個位置初始化，才能進行正常的開始
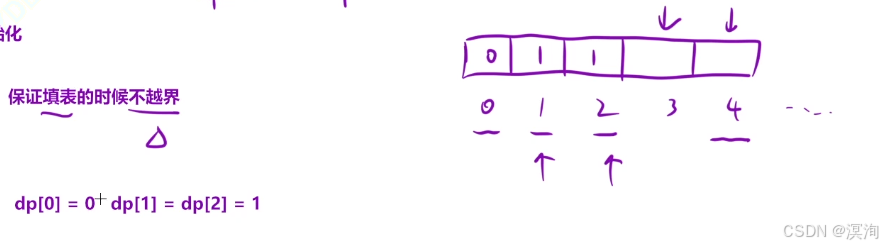
填表順序
1. 需要在求第 i 位置那么： i - 1、i - i、i -3 三個位置的值都得算好
2. 所以需要：從左向右
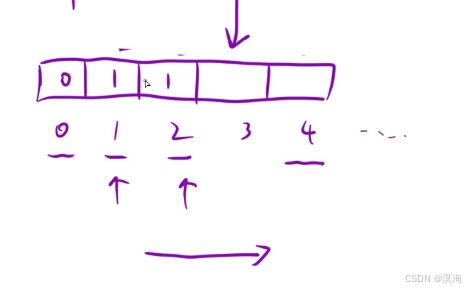
返回值
1. 題目要求：第 n 個的值 dp[ n ]即可
空間優化：當我們在填某個表，某個狀態只需要前面的若干個狀態時，就可以使用滾動數組進行優化，本題僅需要某個數的前3個即可
1. 本題僅需要3個變量abc來標明前3個數，求d的數
2. 通過移動 abcd 四個數，來代替dp表

源碼🗒?

class Solution {
public:int tribonacci(int n) {//1. 狀態表示：dp[i] = 第i個泰波那契序列//2. 狀態表示：Tn+3 = Tn + Tn+1 + Tn+2 -> dp[i] = dp[i-1] + dp[i-2] + dp[i-3]vector<int> dp(n + 1);//提前開辟好 n 個位置的空間，注意從0開始所以+1//3. 初始化：需要前三個 那么就是初始化 0 1 2，從3開始dp[0] = 0,dp[1] = 1,dp[2] = 1;//4. 填表順序：要求的值是Ti，那么求就是 dp[i]，所以肯定是從小的開始，也就是從左往右for(int i = 3;i <= n;i++){dp[i] = dp[i-1] + dp[i-2] + dp[i-3];//這里本質就是使用狀態轉移方程}//5. 返回值：dp[i]即可return dp[n];}int tribonacci(int n) {//空間優化寫法：int a = 0,b = 1,c = 1;int ret = 0;if(n == 0) return 0; if(n == 1 || n == 2) return 1; for(int i = 3 ; i <= n;i++){//填表順序ret = a + b + c;a = b;b = c;c = ret;}return ret;}
};

2. 三步🚶問題

題目👻：

在這里插入圖片描述

分析題目并提出，解決方法🫏：

這里主要理解成：

本題分析不難看出：要求到達某個臺階的方法（這里就能簡單的看出來狀態表示）
直接拿示例一來看：如何到達臺階n=3：
1. 也很簡單：因為小孩每次可以走1/2/3步，那么那幾個階能到達呢？
2. 無非就是 n - 1、n - 2 、n - 3 （這里n=3，故從0 1 2階能到達這里就能看出來狀態轉移方程： dp[n] = dp[n-1] + dp[n-2] + dp[n-3]）
3. 那么要初始化的就是 dp[0]、dp[1]、dp[2]
4. 從狀態表示也能很簡單的推出，因為本質階梯不高：
  1. dp[0]：走到0，那么就是不用走也就是走0步，故為1
  2. dp[1]：走到1，只能從0走一步，故也為1
  3. dp[2]：走到2，那么就能從0走2步和從1走1步，所以為2
5. 剩下就是移動方向：自然和上題一樣從左往右、返回dp[n]即可

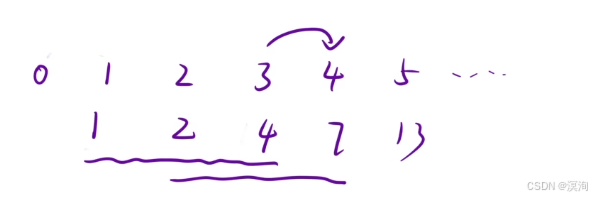
再拿走到4來看：

向下的 1 2 3 個臺階，如能到達4的就是 3 2 1
那么到達4的方法就是：到達 3 2 1 臺階的方法之和

在這里插入圖片描述

題解核心邏輯🚶：

現在推出來了：

狀態表示（經驗 (以某個位置結尾/以某個位置起始) + 題目要求）
1. dp[ i ] 表示到達i個臺階一共有多少個方法
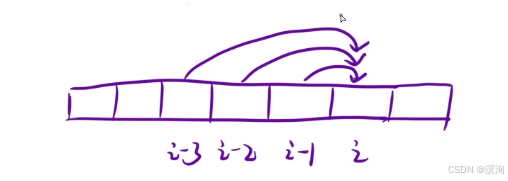
狀態轉移方程：以 i 位置的狀態，最近的一步，來劃分問題
1. dp[i] 分為三種情況：
2. 從 i - 1 -> i：dp[ i - 1 ]
3. 從 i - 2 -> i：dp[ i - 2 ]
4. 從 i - 3 -> i：dp[ i - 3 ]
5. 所以：dp[ i ] = dp[ i - 1 ] + dp[ i - 2 ] + dp[ i - 3 ]
初始化：
1. dp[0] = 1
2. dp[1] = 1
3. dp[2] = 2
填表順序：從左往右
返回值：dp[n]

class Solution {
public:int waysToStep(int n) {//1. 狀態表示：dp[n] 計算小孩上到 n 階臺階有多少種上樓梯的方式//2. 狀態方程：dp[i] = dp[i-1] + dp[i-2] + dp[i-3] 本質還是很上題一樣vector<int> dp(n+3);//這里的初始化同樣要注意因為可能n較小所以需要+3//3. 初始值：同樣的 0 1 2，但本題的初始化就沒那么簡單了// 也希望你能很好的體會 狀態表示的作用：確定每個狀態點i位置的值dp[0] = 1;//到達0階有幾種dp[1] = 1;//到達1階有幾種dp[2] = 2;//到達2階有幾種if(n <= 2) return dp[n];//4. 方向：同樣需要求 i 就得先找到 i-3... 那么就得從左往右for(int i = 3;i <= n;i++){dp[i] = ((long)dp[i-1] + dp[i-2] + dp[i-3]) % 1000000007;//這里本質就是使用狀態轉移方程}//5. 返回dp[n]即可return dp[n];}//寫法二：int waysToStep(int n) {vector<int> dp(n + 3);dp[1] = 1;dp[2] = 2;dp[3] = 4; //另外一種看法忽律0臺階直接從1開始，方法類似不過多敘述for(int i = 4;i<=n;i++){dp[i] = ((long)dp[i-1] + dp[i-2] + dp[i-3]) % 1000000007;}return dp[n];}
//寫法三：
//這里優化就不寫了貼一份別人的：作者：Spectreint waysToStep(int n) {// 時間復雜度O(N)，空間復雜度O(1)if (n == 1 || n == 2) return n;if (n == 3) return 4;int dp1 = 1, dp2 = 2, dp3 = 4, dp4;for (int i = 4; i <= n; ++i) {dp4 = ((dp1 + dp2) % 1000000007 + dp3) % 1000000007;dp1 = dp2;dp2 = dp3;dp3 = dp4;}return dp4;}};

在這里插入圖片描述

3. 使用最小花費爬樓梯🪜

題目📕：

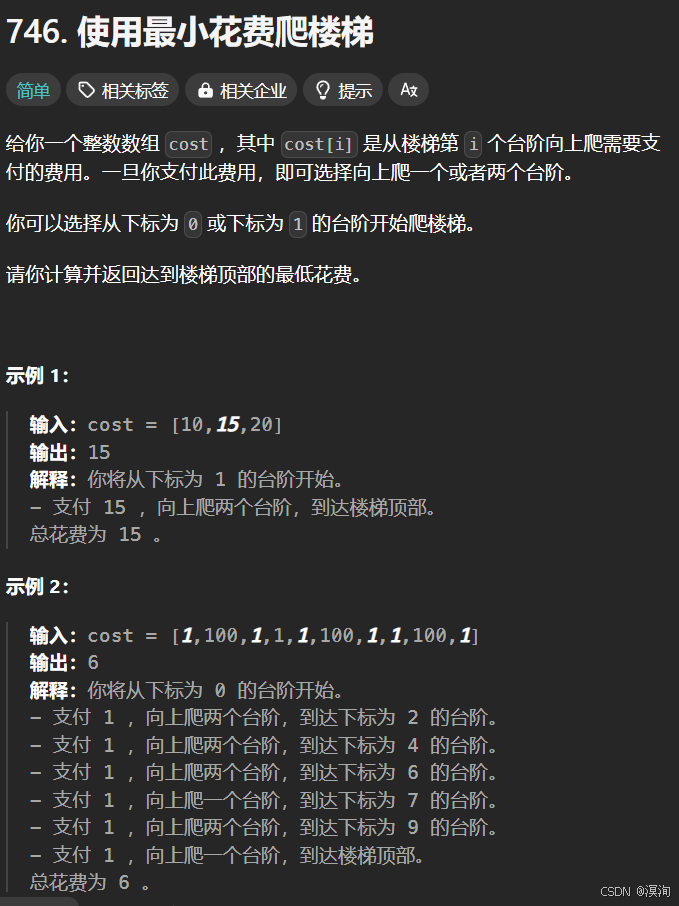
在這里插入圖片描述

分析題目并提出，解決方法??：

樓頂在最后

題解核心邏輯🎈：

解法一：

狀態表示（經驗+題目要求）：
1. 以 i 位置為結尾，xxx：
2. 所以：dp[ i ] 表示：到達 i 位置時，最小花費
狀態轉移方程
1. 用之前或者之后的狀態，推導出dp[ i ] 的值
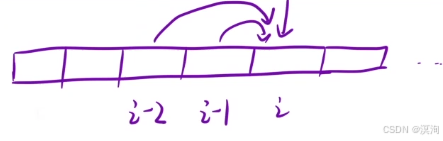
2. 根據最近的一步，來劃分問題
3. 先到達 i - 1，然后支付 cost[ i-1 ]，走一步：dp[ i - 1] + cost[ i - 1 ]
4. 先到達 i - 2，然后支付 cost[ i-2 ]，走兩步：dp[ i - 2 ] + cost[ i - 2]
5. 所以dp[ i ] = min( dp[ i - 1] + cost[ i - 1 ] , dp[ i - 2 ] + cost[ i - 2] )
初始化（防止越界，因為會用到 i - 1 和 i - 2 兩個位置的值）：
1. 因為dp[ 0 ] = dp[ -1 ] + dp[ -2 ]這是沒必要的，從題目可知
2. 0 1 臺階是0元，所以直接從 2 開始即可
3. 所以初始化 dp[0] = dp[1] = 0
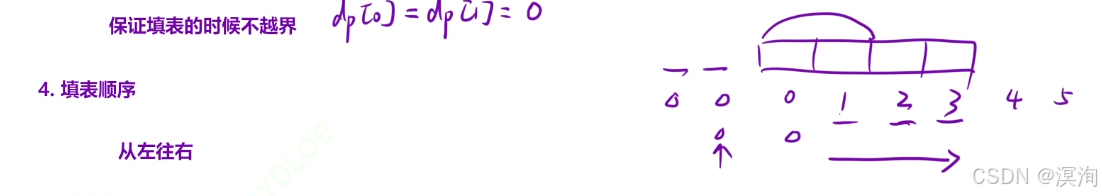
填表順序：由題意從左往右
返回值：dp[n]

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {// cost[i] 是從樓梯第 i 個臺階向上爬需要支付的費用// 爬到樓頂本質就是超過容器個數 size=3 就需要爬到4（下標3）// 1. dp[i]:到達第i層需要的 最小 花費int n = cost.size();vector<int> dp(n+1); // 2. 狀態轉移方程： dp[i] = min(dp[i-1],dp[i-2]) + cost[i] 因為只能從下兩層爬上來 + 當前需要的價值，注意的是cost[size]是越界的，此時+0即可// 3. 初始化：最小情況： dp[2] = min(dp[1],dp[0]) + cost[2] ，故初始化dp[1] dp[2] 即可dp[1] = cost[1];dp[0] = cost[0];for(int i = 2;i<= n;i++){if(i == n) dp[i] = min(dp[i-1],dp[i-2]);else dp[i] = min(dp[i-1],dp[i-2]) +cost[i];}return dp[n];}
};

在這里插入圖片描述

方法二👻：

狀態表示：
1. 以 i 位置為起點，xxx
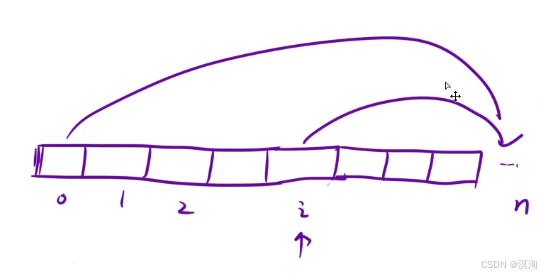
2. dp[ i ]：從 i 位置開始，到達樓頂，此時的最小花費
狀態轉移方程
1. 用之前或者之后的狀態推導
2. 支付cost[i]，往后走一步，從 i + 1 位置出發到達終點 dp[ i + 1 ] + cost[ i ]
3. 支付 cost[ i ]，往后走兩步，從 i + 2 位置出發到達終點 dp[ i + 2 ] + cost[ i ]
4. dp[ i ] = min( dp[ i + 1 ] + cost[ i ],dp[ i + 2 ] + cost[ i ])；
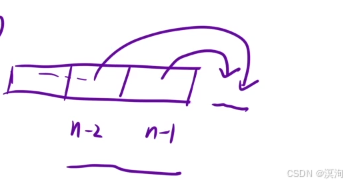
初始化：
1. dp[ n - 1 ] = cost [ n - 1 ]
2. dp [ n - 2 ] = cost[ n - 2 ]
填表順序：從右往左
返回值：min(dp[0]，dp[1])

這里就不擴展寫了，感興趣的可以實踐下

中斷總結🗒?一下：

通過上述好幾道題不難總結出常用的狀態表示經驗：
1. 以 i 位置為結尾，xxx
2. 以 i 位置為開始，xxx

🥴通過上述三道題，估計你對動態規劃中的最基本的步驟和思想都有一定的認識了，下面就不將是簡單的套公式了，而是結合一些內容進一步深化對動態規劃的理解
也就需要你在抽象的題目中提解出動態規劃~~🤔
🤓本質也就是：狀態表示不簡單了、狀態方程也沒那么好推導了

4. 解碼方法

題目🪜：

在這里插入圖片描述

分析題目并提出，解決方法??：

在這里插入圖片描述
本題如何想到的呢：從最后一個節點來看，不難發現規律：

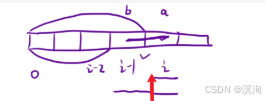
要求第i位置的能否解碼，就只用考略
1. 當前位置i是否符合（0 <= i <= 9）
2. i位置與i-1位置結合時是否符合(10 <= i-1 + i <= 26)
要求總共的解碼個數，則是通過dp表存儲每個節點的解碼個數，最小的情況是很容易推算的，所以使用動規中的dp表是能進行存儲的
通過上面兩個想法也就不難得出狀態轉移方程如何計算
1. 判斷能否解碼的兩種方法，看這兩種方法那個符合條件，若符合條件就記錄上存儲進dp表中
2. 若不能解碼的當然就不計算
3. 具體見下面詳細五步

題解核心邏輯🎈：

狀態表示：
1. 以 i 結尾時，解法方法的總數
狀態轉移方程
1. 根據最近的一步劃分問題：
2. 分為兩種情況：
  1. dp[ i ]單獨解碼（ 1 ~ 9 ）：解碼成功（個數為 dp[ i -1 ]：因為本質就是拼接了一個新字母🤔這里好好理解下，并不用+1哦），失敗則為0
  2. dp[ i ] 與 dp[ i - 1 ] 結合解碼（ 10 ~ 26 ）：解碼成功（dp[ i - 2 ] 本質就是拼接兩個新字母），失敗則為0
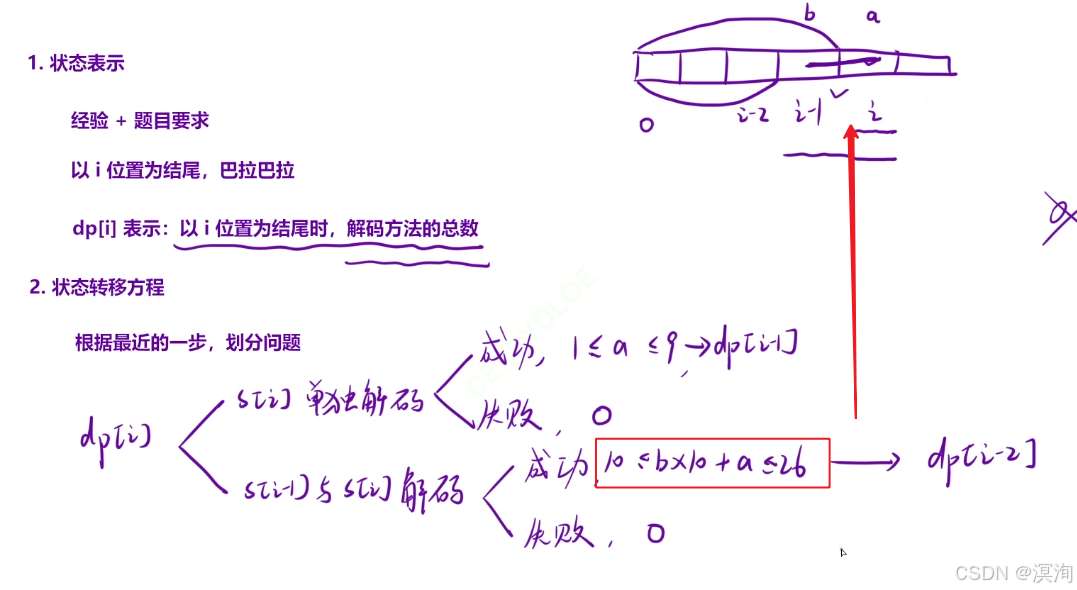
初始化：dp[ 0 ] 、dp[ 1 ]
填表順序：根據狀態轉移方程得知從左往右
返回值：dp[ n - 1 ]，n - 1最后一個位置

優化：處理邊界問題以及初始化問題的技巧🤓

整個數組多開一位，然后通過使用這個多開的一位虛擬節點的初始化來幫助運算
注意的事項：

虛擬節點的初始化是根據題目意思來的，保證后面填表的正確
1. 一般來說填寫0
2. 但本題對于該虛擬節點的使用，為了求原dp表中的dp[ 1 ] 時使用的 dp[ i - 2 ]
3. 因為假設 dp[ 1 ] 和移動后就變成了 dp[ 2 ]，此時要求dp[ 2 ] 需要dp[ 1 ] 和 dp [ 0 ]
4. dp [ 1 ] 本質就是原dp數組中的dp[ 0 ] 所以不會有問題
5. 但dp[ 0 ] 就需要我們自己控制，回顧狀態轉移方程，這里dp[ i - 2 ]的作用是當 i 和 i - 1結合成功時取的值，所以填1（因為前面也沒字符判斷了，所以填1給到dp[2]，代表正確）
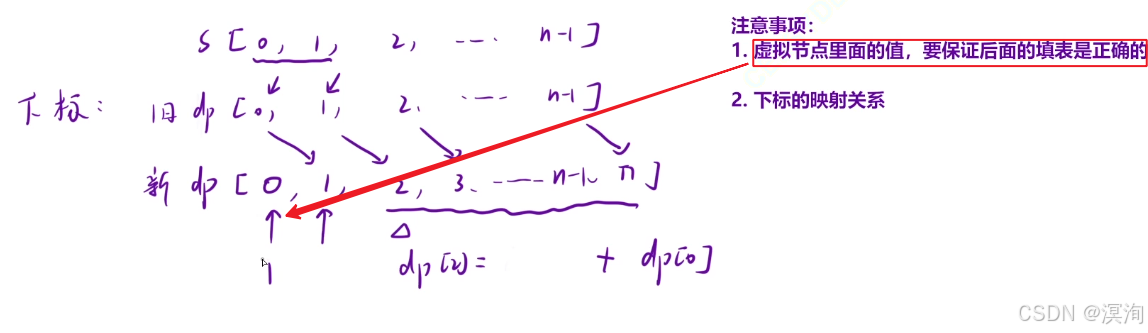
注意下標的映射關系，在真正使用dp時，因為dp表是多一格，對于s字符串中的下標要 - 1：s[i-1]

class Solution {
public:int dp[101] = {};int numDecodings(string s) {//初始化 0 和 1dp[0] = 1;//虛擬節點if( 1 <=  s[0] - '0' &&  s[0] - '0' <= 9) dp[1] = 1 ;//原dp[0]//移動s字符下標完成：for(int i = 2; i <= s.size();i++){//單個字符int onechar = s[i - 1] - '0'; if( 1 <= onechar && onechar <= 9) dp[i] += dp[i-1];//兩個字符int combine = (s[i - 2] - '0') * 10 + onechar;if(10 <= combine && combine <= 26) dp[i] += dp[i-2];if(dp[i] == 0) return 0;}return dp[s.size()];}
};解法二：
class Solution {
public:int numDecodings(string s) {//dp[i]：以i位置結尾的解碼個數：//dp[i] = dp[i-1] + dp[i-2]，其中若若不能解碼則不進行相加，或者加0//初始化：因為s.length >= 1，所以需要一個多的空位，來特殊處理等于1的情況int n = s.size();vector<int> dp(n+2);//結果存在n下標dp[0] = 1; //默認解碼個數為1次dp[1] = 1; //默認解碼個數為1次if(s[0] == '0') return 0;//處理dp下標完成存儲效果for(int i = 0; i < n;i++){//不要簡單的字符判斷！！！！！！！！！！！// if(i-1 >= 0 && s[i-1] - '0' >= 1 && s[i-1] - '0' <= 2 && //    s[i] - '0' >= 0 && s[i] - '0' <= 6) dp[i+2] += dp[i];int val = s[i] - '0';if(val >= 1 && val <= 9) dp[i+2] += dp[i+1];int combine = i-1 >= 0 ? ( s[i-1] - '0') * 10 + val : -1;if(combine >= 10 && combine <= 26)  dp[i+2] += dp[i];}return dp[n+1];}
};