目錄
一. 樹的概念和結構
1.1 樹的基本概念
1.2 樹的結構特點
二. 樹的表示方法和實際運用
2.1 孩子 - 兄弟表示法(Child-Sibling Representation)
2.2 樹的實際應用場景
三. 二叉樹的概念
3.1 二叉樹的核心定義
3.2 二叉樹的基本分類
四. 二叉樹的性質
性質 1:節點數量與層數的關系
性質 2:深度與總節點數的關系
性質 3:葉子節點與度為 2 的節點的關系
性質 4:完全二叉樹的深度
性質 5:完全二叉樹的節點索引關系
五. 二叉樹的存儲結構
一、順序存儲結構
二、鏈式存儲結構
一. 樹的概念和結構
在數據結構中,樹(Tree)?是一種非線性的數據結構,它由節點(Node)和邊(Edge)組成,用于表示具有層次關系的數據。樹的結構類似于自然界中的樹,具有 “根”、“枝”、“葉” 等概念,但其形態是 “倒置” 的(根在上,葉在下)。
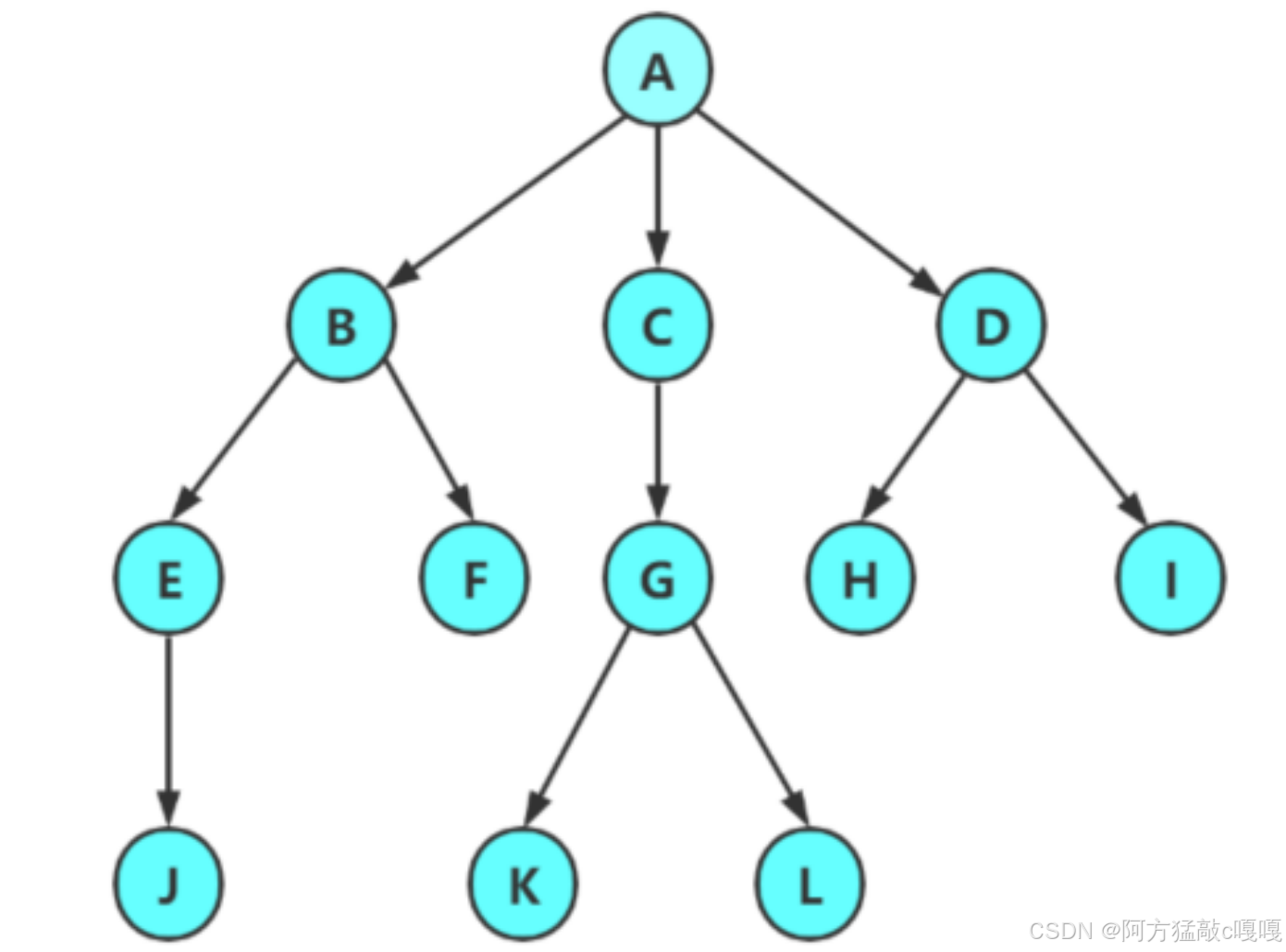
由上圖可以推測出? 每一個節點只有向上和向下鏈接 如果出現了左右鏈接 則不是樹結構 如下:

1.1 樹的基本概念
節點(Node)
樹的基本組成單位,包含數據和指向子節點的引用(指針)。根節點(Root)
樹的起點,沒有父節點的節點(一棵樹有且僅有一個根節點)。父節點與子節點
若節點 A 直接指向節點 B,則 A 是 B 的父節點,B 是 A 的子節點。
同一父節點的子節點互稱為兄弟節點。
葉子節點(Leaf)
沒有子節點的節點(即度為 0 的節點)。度(Degree)
一個節點擁有的子節點數量(葉子節點的度為 0,根節點的度至少為 1)。深度(Depth)
從根節點到當前節點的路徑長度(根節點深度為 0 或 1,通常以 0 開始)。高度(Height)
從當前節點到最深葉子節點的路徑長度(葉子節點高度為 0,根節點高度即樹的高度)。路徑(Path)
從一個節點到另一個節點經過的節點序列(樹中路徑唯一,無環)。子樹(Subtree)
以某節點為根的所有后代節點組成的樹(該節點及其子樹是原樹的一部分)。
1.2 樹的結構特點
- 非線性結構:節點之間的關系不是線性的,而是層次化的。
- 無環性:任意兩個節點之間有且僅有一條路徑,不存在回路(環)。
- 根的唯一性:只有一個根節點,所有其他節點都直接或間接依附于根。
- 子樹獨立性:一棵樹的子樹之間互不相交(否則會形成環)。
二. 樹的表示方法和實際運用
樹的表示方法有很多 現在我向大家介紹孩子兄弟表示法
2.1 孩子 - 兄弟表示法(Child-Sibling Representation)
- 原理:將任意樹轉換為二叉樹結構,每個節點包含三個部分:
- 數據域;
- 第一個子節點指針(指向最左子節點);
- 右兄弟節點指針(指向同一父節點的下一個兄弟節點)。
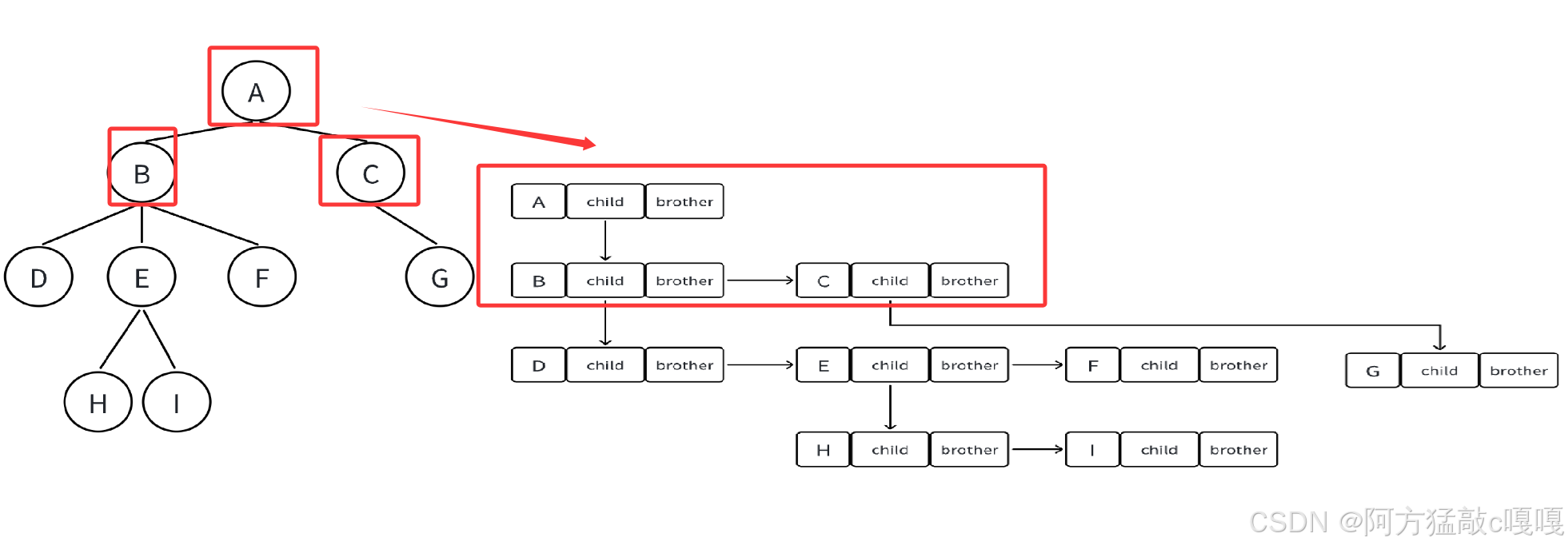
- 結構示例(將多叉樹轉為二叉樹):
(原樹中 A 的子節點是 B、C、D;B 的子節點是 E、F)A/B → C → D (B的右兄弟是C,C的右兄弟是D)/E → F (E的右兄弟是F) - 優點:將多叉樹統一為二叉樹結構,可復用二叉樹的算法(如遍歷、插入),節省空間。
- 缺點:結構較抽象,需理解 “兄弟節點” 的轉換邏輯。
- 適用場景:多叉樹與二叉樹的轉換(如森林的表示、語法樹的存儲)。
struct TreeNode
{struct Node* child; // 左邊開始的第?個孩?結點struct Node* brother; // 指向其右邊的下?個兄弟結點int data; // 結點中的數據域
};
2.2 樹的實際應用場景
樹的層次化、無環特性使其在解決具有 “父子關系”“層級分類” 的問題時極為高效,以下是典型場景:
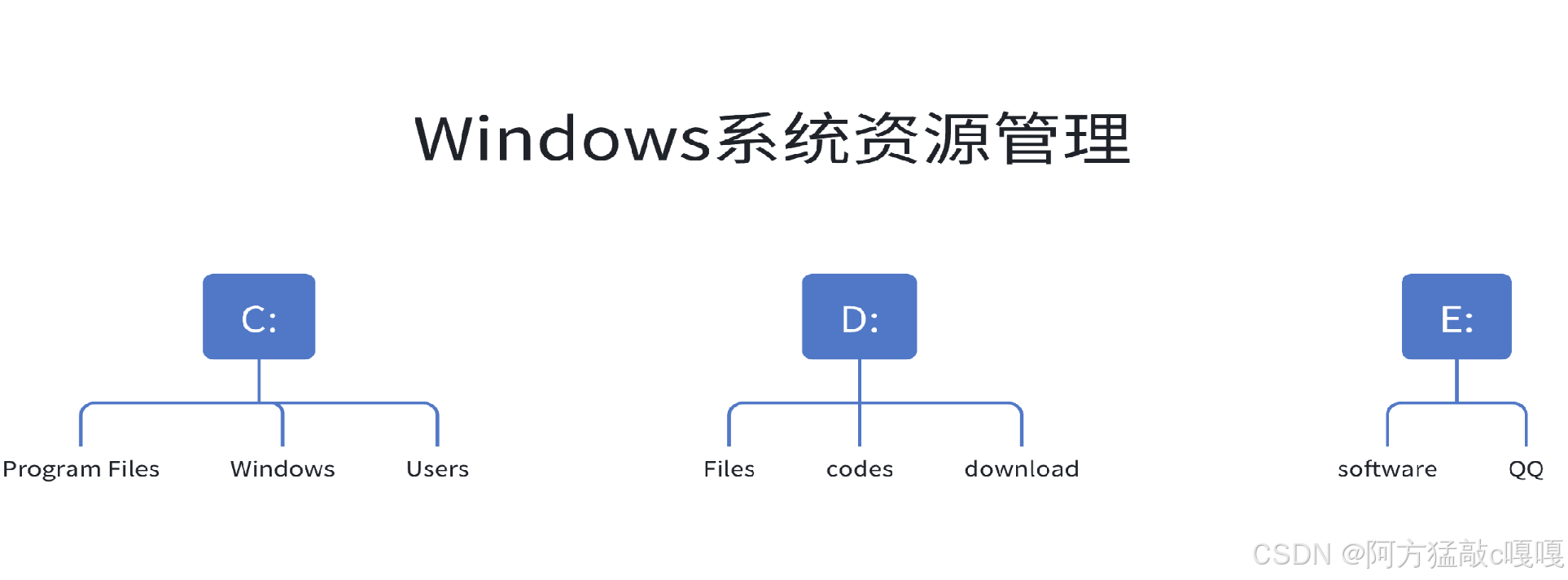
1.?文件系統與目錄結構
- 原理:操作系統的文件和文件夾以樹狀組織,根目錄為根節點,文件夾為中間節點,文件為葉子節點。
- 示例:Windows 的
C:\Users\Document\file.txt是一條從根到葉子的路徑。- 優勢:支持高效的路徑查找(如
cd命令遍歷目錄)和層級管理。2.?數據庫索引
- 原理:B 樹、B + 樹等多叉樹結構被用于數據庫索引,平衡的樹高保證了查詢、插入、刪除的高效性(時間復雜度 O (log n))。
- 示例:MySQL 的 InnoDB 存儲引擎使用 B + 樹作為聚簇索引,葉子節點存儲完整數據行,非葉子節點作為索引指引。
三. 二叉樹的概念
下面向大家介紹樹中最常見也是最常用的結構---二叉樹
二叉樹(Binary Tree)是一種特殊的樹結構,每個節點最多有兩個子節點,分別稱為左子節點和右子節點。這種 “最多兩個子節點” 的特性使其結構相對簡單,同時具備樹的層次化、非線性特點,是數據結構中最常用的樹類型之一。
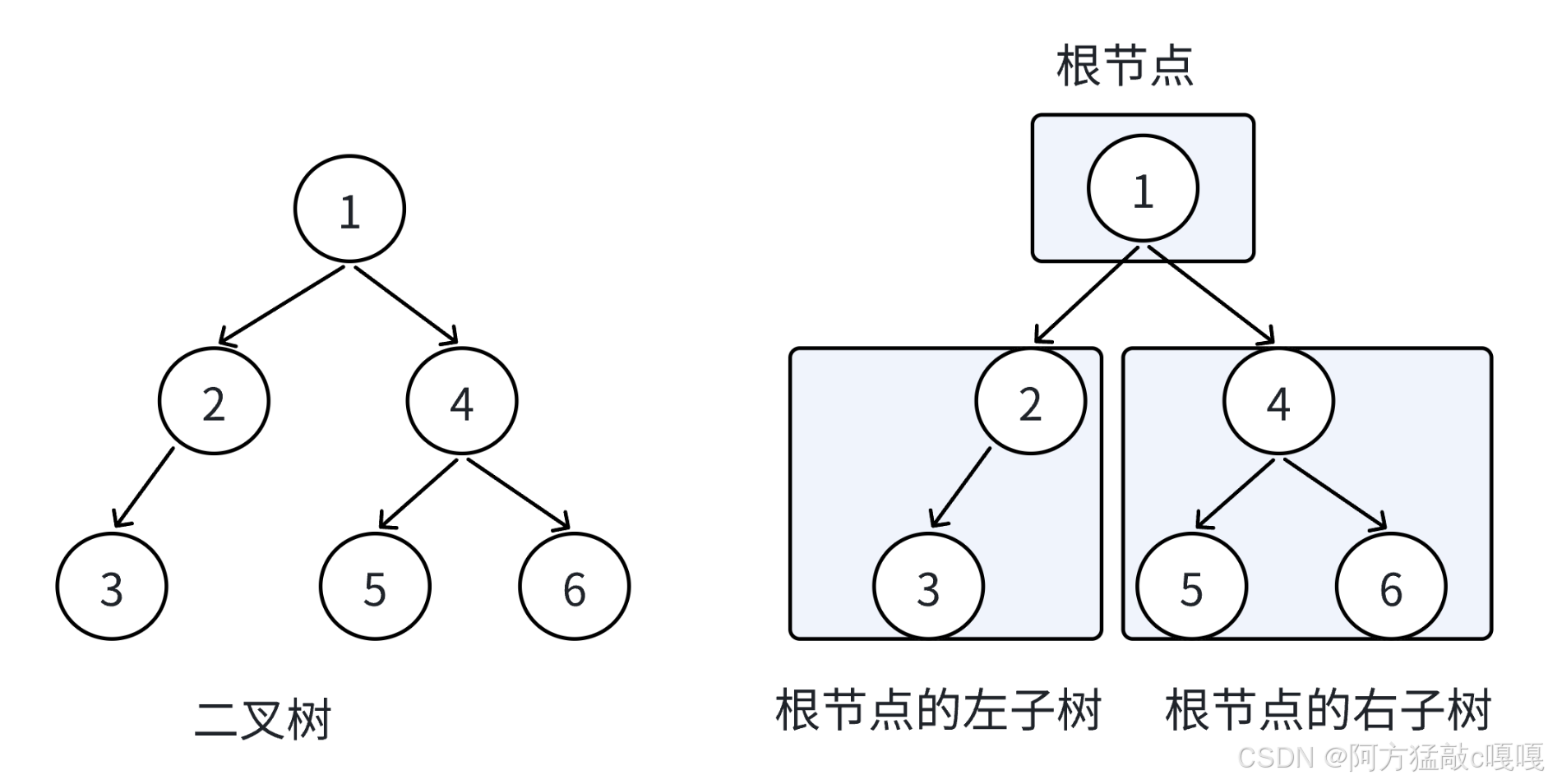
從上圖可以看出 二叉樹即最多二分叉 所以最多只有兩個子節點 下面看一下二叉樹的核心定義
3.1 二叉樹的核心定義
-
節點結構:每個節點包含三部分:
- 數據域(存儲節點值);
- 左子節點指針(指向左側子節點,無則為
null); - 右子節點指針(指向右側子節點,無則為
null)。
-
基本特性:
- 根節點:無父節點的節點(二叉樹有且僅有一個根節點,除非是空樹)。
- 葉子節點:左、右子節點均為
null的節點(無子女)。 - 子樹:以某個節點的左 / 右子節點為根的樹,稱為該節點的左 / 右子樹(子樹本身也是二叉樹)。
- 層次(深度):根節點為第 1 層,其子節點為第 2 層,以此類推。
- 高度:節點到最深葉子節點的路徑長度(葉子節點高度為 1)。
3.2 二叉樹的基本分類
-
空二叉樹:沒有任何節點的樹。
-
滿二叉樹(Full Binary Tree):
- 所有非葉子節點都有兩個子節點;
- 所有葉子節點在同一層次(即最后一層)。
例如 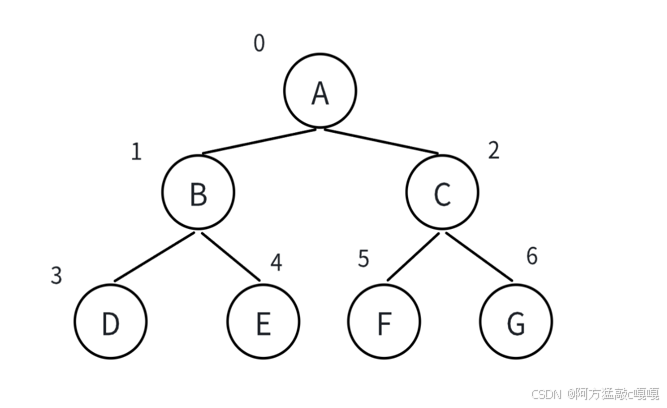
-
完全二叉樹(Complete Binary Tree):
- 除最后一層外,所有層的節點數都達到最大值;
- 最后一層的節點從左到右連續排列(不允許右側有空缺);
- 滿二叉樹是完全二叉樹的特例。
例如(最后一層節點從左到右連續):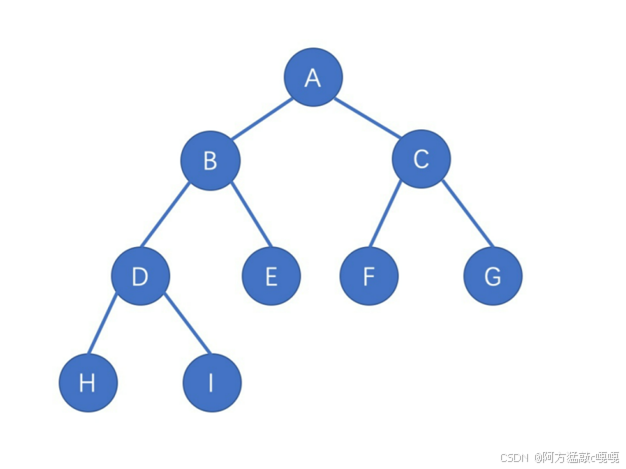
滿二叉樹屬于一種特殊的完全二叉樹 關系圖如下
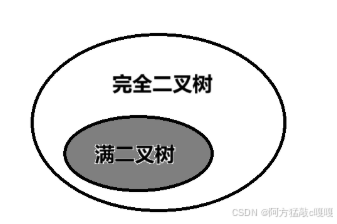
四. 二叉樹的性質
性質 1:節點數量與層數的關系
第?i?層最多有?2^(i-1)?個節點(i ≥ 1,層數從 1 開始計數)。
推導:第 1 層(根節點)最多 1 個節點(
2^0);第 2 層最多 2 個節點(2^1);第 3 層最多 4 個節點(2^2)…… 第i層最多為?2^(i-1)?個節點(每一層節點數是上一層的 2 倍,因每個節點最多 2 個子節點)。
性質 2:深度與總節點數的關系
深度為?k?的二叉樹,最多有?2^k - 1?個節點(k ≥ 1)。
推導:總節點數為各層最大節點數之和,即?
2^0 + 2^1 + 2^2 + ... + 2^(k-1) = 2^k - 1(等比數列求和)。特例:滿二叉樹的總節點數恰好為?
2^k - 1(每一層都達到最大節點數)。
性質 3:葉子節點與度為 2 的節點的關系
對任何一棵二叉樹,若葉子節點數為?n?,度為 2 的節點數為?n?,則?n? = n? + 1。
-
推導:
-
設度為 1 的節點數為?
n?,總節點數?N = n? + n? + n?。 -
二叉樹中,除根節點外,每個節點都有且僅有一個父節點,因此總邊數為?
N - 1(邊數 = 節點數 - 1)。 -
邊數也可由節點的度計算:度為 1 的節點貢獻 1 條邊,度為 2 的節點貢獻 2 條邊,葉子節點(度為 0)貢獻 0 條邊,因此總邊數?
= n?×1 + n?×2。 -
聯立得:
n? + n? + n? - 1 = n? + 2n?,化簡后?n? = n? + 1。
-
性質 4:完全二叉樹的深度
具有?n?個節點的完全二叉樹,其深度為??log?n? + 1(?x??表示向下取整)。
-
推導:
-
設深度為?
k,則完全二叉樹的節點數?n?滿足:
深度為?k-1?的滿二叉樹節點數 <?n?≤ 深度為?k?的滿二叉樹節點數,
即?2^(k-1) - 1 < n ≤ 2^k - 1。 -
不等式變形為?
2^(k-1) ≤ n < 2^k,兩邊取對數得?k-1 ≤ log?n < k,因此?k = ?log?n? + 1。
-
性質 5:完全二叉樹的節點索引關系
對有?
n?個節點的完全二叉樹,若按層次(從左到右)給節點編號(從 1 開始),則對任意節點?i(1 ≤ i ≤ n):
若?
i > 1,則其父節點編號為??i/2?(左子節點的父節點為?i/2,右子節點的父節點為?(i-1)/2,統一為??i/2?)。若?
2i ≤ n,則其左子節點編號為?2i;否則無左子節點(葉子節點)。若?
2i + 1 ≤ n,則其右子節點編號為?2i + 1;否則無右子節點。例:編號為 3 的節點,父節點為?
?3/2? = 1,左子節點為?6(若存在),右子節點為?7(若存在)。
這些性質是二叉樹遍歷、構建(如堆的實現)、操作(如查找父 / 子節點)的理論基礎,尤其在完全二叉樹和滿二叉樹中應用廣泛。
五. 二叉樹的存儲結構
二叉樹的存儲結構需要兼顧其邏輯特性(節點間的父子關系)和操作效率(如訪問子節點、父節點),常見的存儲方式有兩種:順序存儲結構和鏈式存儲結構。
一、順序存儲結構
順序存儲通過數組存儲二叉樹的節點,利用節點在數組中的索引位置反映其邏輯關系(父子、左右兄弟)。
適用場景:完全二叉樹(或滿二叉樹),此時數組空間利用率最高;非完全二叉樹會浪費較多空間。
存儲規則
按層次遍歷順序(從根到葉,每層從左到右)將節點存入數組,索引從?0?或?1?開始(通常從?1?開始,便于計算父子關系)。
假設數組索引從?1?開始,對于任意節點?i:
- 左子節點索引:
2i(若存在); - 右子節點索引:
2i + 1(若存在); - 父節點索引:
i // 2(i > 1?時)。
示例
完全二叉樹的順序存儲:
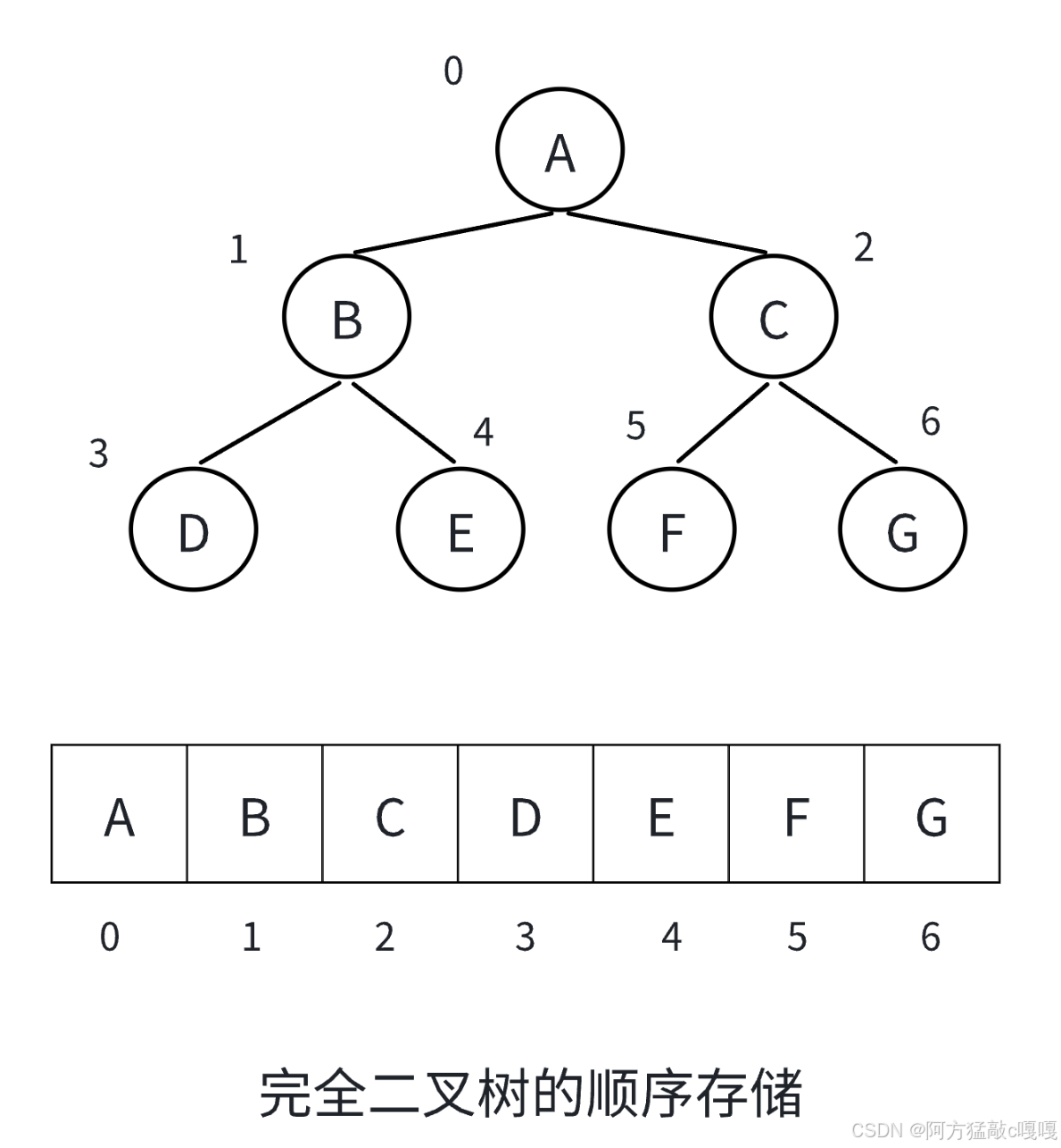
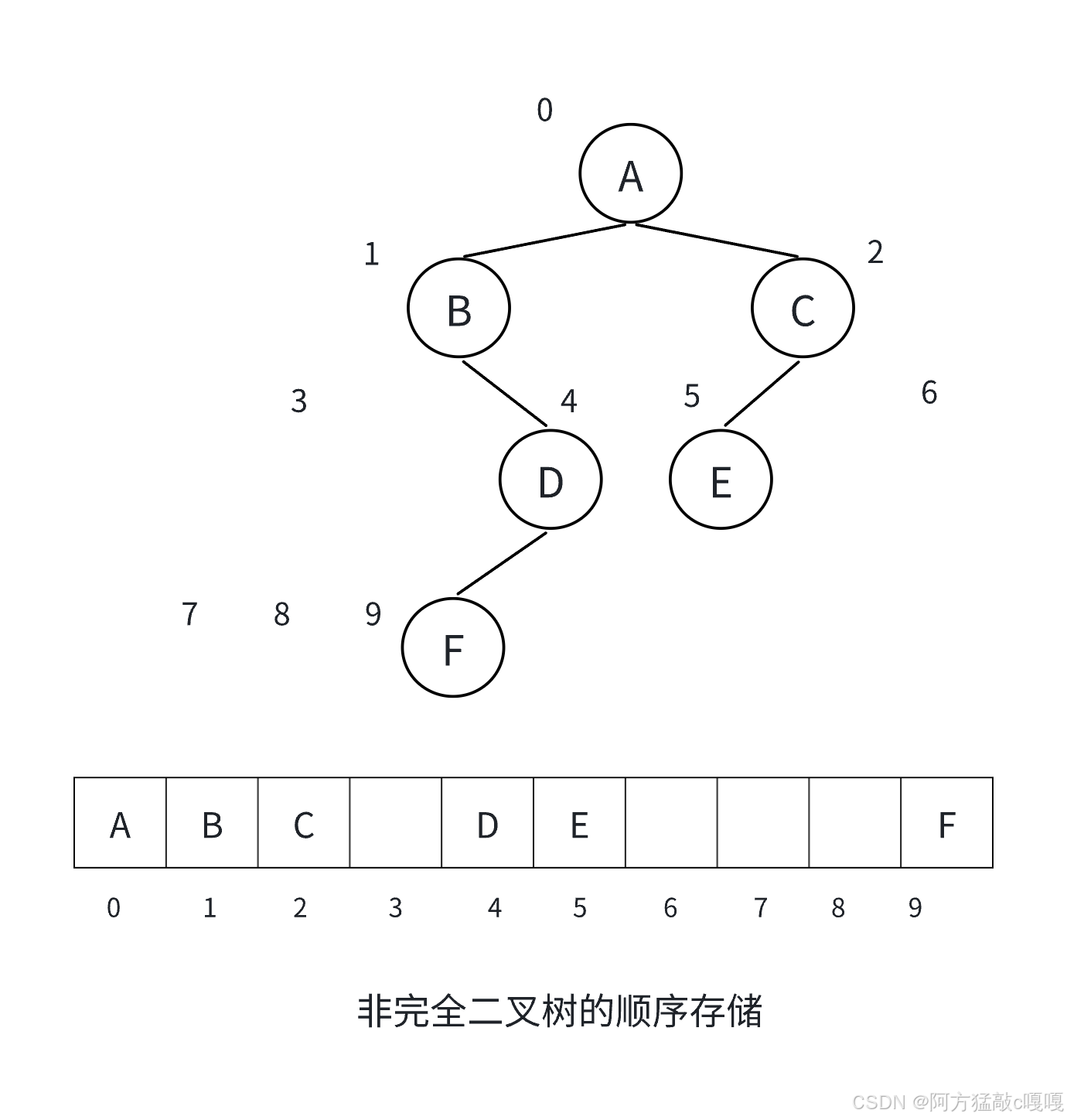
優缺點
- 優點:訪問子節點 / 父節點效率高(通過公式直接計算索引,時間復雜度?
O(1));適合完全二叉樹(無空間浪費)。 - 缺點:非完全二叉樹需用?
null?填充空缺位置,空間利用率低;插入 / 刪除節點時可能需要大量移動元素,效率低。
二、鏈式存儲結構
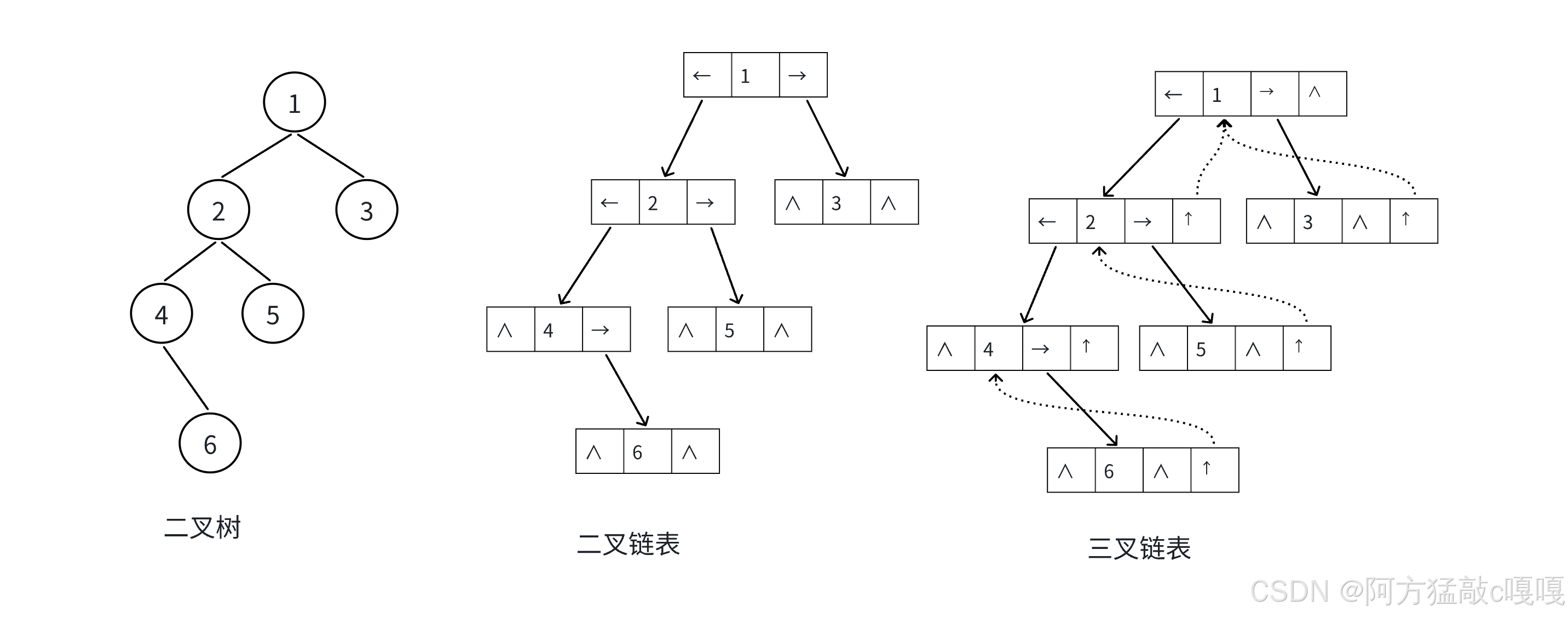
鏈式存儲通過指針(或引用)?連接節點,每個節點存儲自身數據及指向子節點的指針,更靈活地表示任意二叉樹。
節點結構
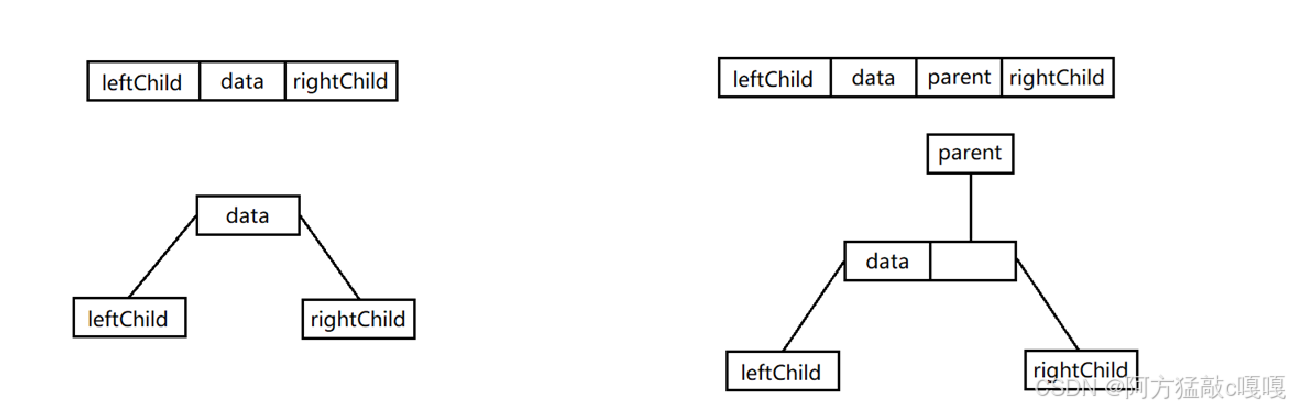
每個節點包含 3 個域:
- 數據域:存儲節點的值;
- 左指針域:指向左子節點(
left); - 右指針域:指向右子節點(
right)。
// C語言示例
typedef struct BiTNode {int data; // 數據域struct BiTNode *left; // 左子節點指針struct BiTNode *right; // 右子節點指針
} BiTNode, *BiTree;
任意二叉樹的鏈式存儲:



——微調Transformer語言模型進行回歸分析)

——系統包管理)







)




)
