代碼主要功能

該Matlab代碼實現了一個KOA-RIME開普勒結合霜冰算法雙重優化的BP神經網絡回歸模型，結合特征貢獻度分析（SHAP）和新數據預測功能。核心功能包括：

1. 雙重參數優化：先用智能算法（以chebyshev映射改進KOA開普勒算法為例）優化隱藏層神經元數量和學習率，再用智能算法（以chebyshev映射改進RIME霜冰算法為例）優化權重/偏置初始值
2. 特征貢獻分析：通過SHAP值量化各輸入特征對輸出的影響
3. 多維度評估：提供RMSE、R2、MAE等指標對比及可視化
4. 一站式流程：數據預處理 → 模型優化 → 訓練預測 → 結果解釋 → 新數據預測
   其中：代碼采用9種映射方法選擇種群初始值,改進KOA和RIME智能算法

9種映射方法包括
1.tent 映射
2.chebyshev 映射
3.singer 映射
4.logistic 映射
5.sine 映射
6.circle 映射
7.立方映射
8.Hénon 映射
9.廣義Logistic映射

以上共計9*2=18種智能算法組合。

算法步驟

1. 數據預處理
   ? 導入Excel數據（回歸數據.xlsx）
   ? 歸一化特征/標簽（mapminmax）
   ? 按7:3劃分訓練/測試集（可選隨機打亂）
2. 第一段優化（以KOA為例）
   ? 優化目標：隱藏層神經元數 + 學習率
   ? 搜索空間：
   lb1 = [floor(sqrt(inp+put)), 0]; % 神經元下限, 學習率下限
   ub1 = [10+ceil(sqrt(inp+put)), 0.1]; % 神經元上限, 學習率上限
   ? 輸出：最優神經元數 besthiddens、學習率 bestlearn
3. 第二段優化（以RIME為例）
   ? 優化目標：權重矩陣(Ⅰ/Ⅱ) + 偏置向量(Ⅰ/Ⅱ)
   ? 變量維度：inpbesthiddens + besthiddens + besthiddensput + put
   ? 輸出：最優初始參數 gBest2
4. 模型構建與訓練
   ? 使用優化參數初始化BP網絡
   ? 設置雙曲正切隱藏層 + 線性輸出層
   ? 訓練1000輪（目標誤差1e-6）
5. 預測與評估
   ? 反歸一化預測結果
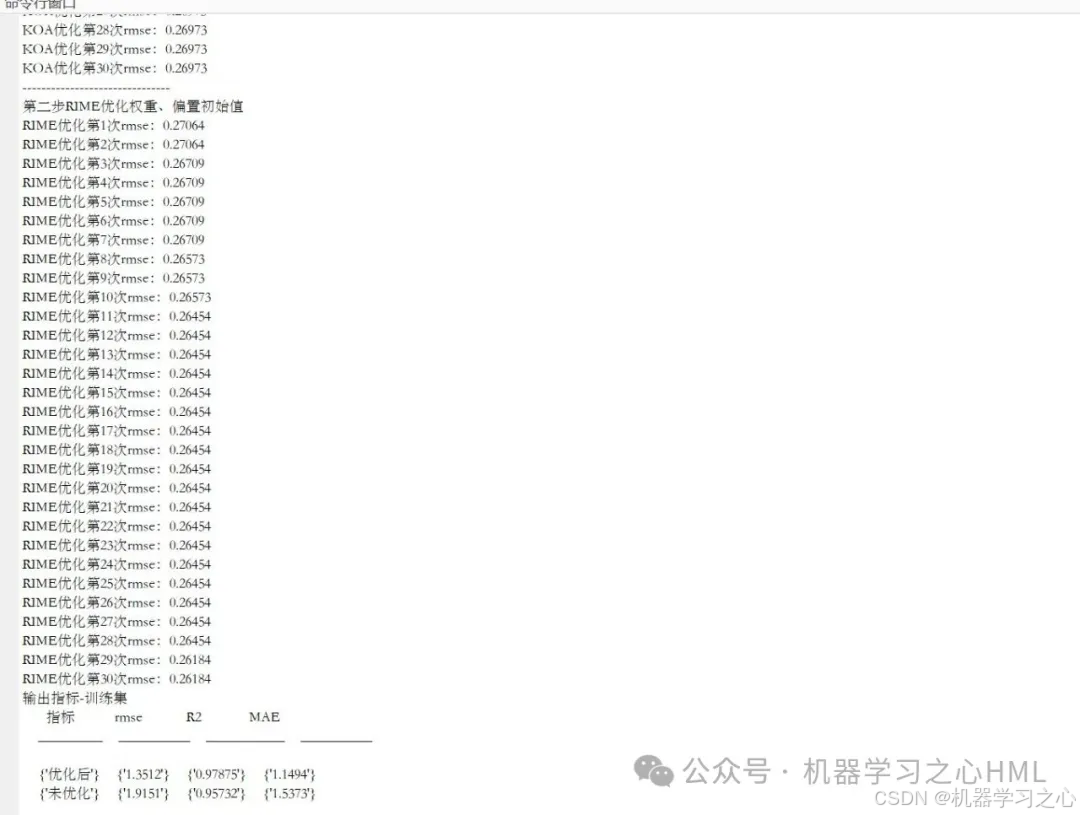
   ? 對比優化/未優化模型的：
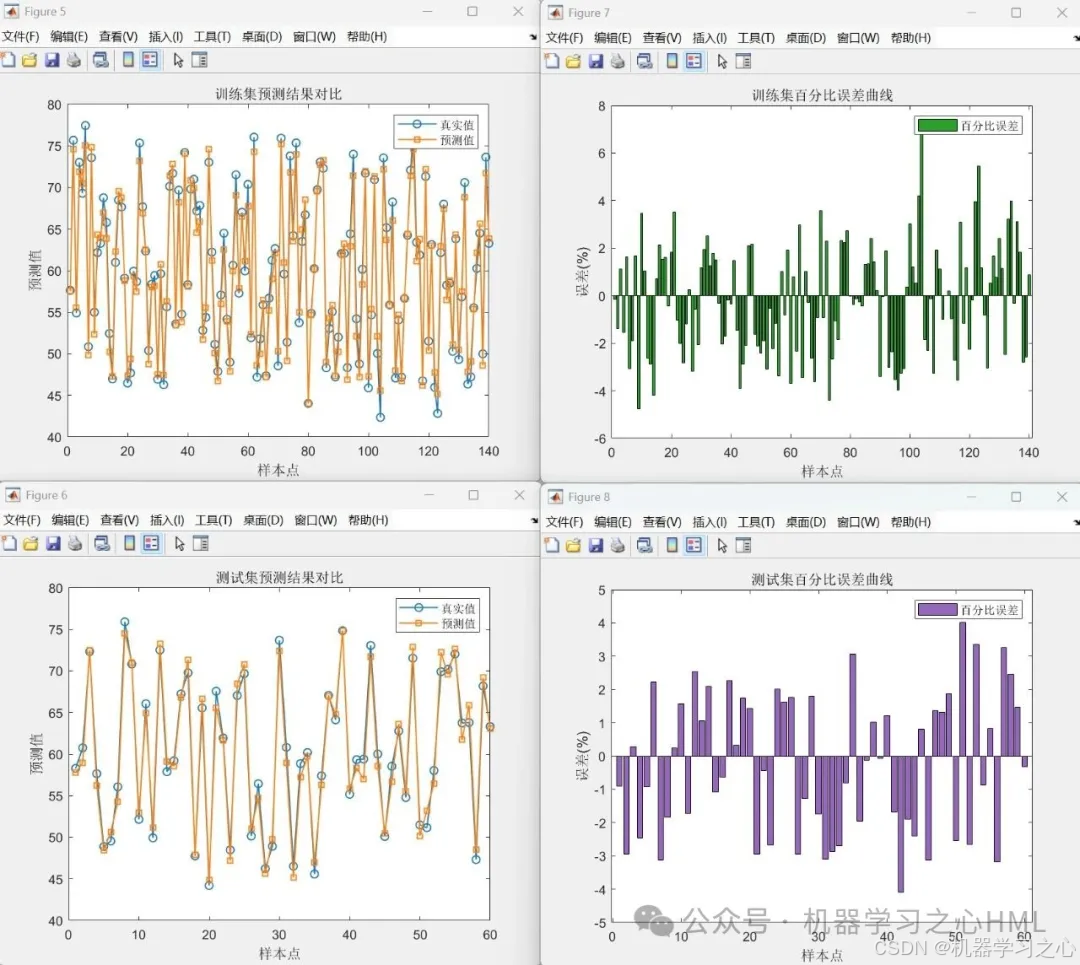
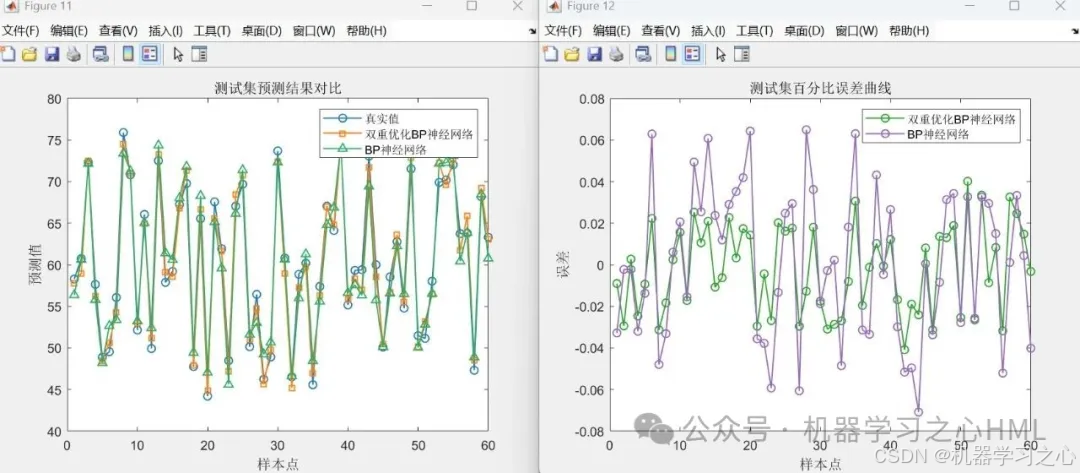
   ? 預測曲線圖
   ? 百分比誤差圖
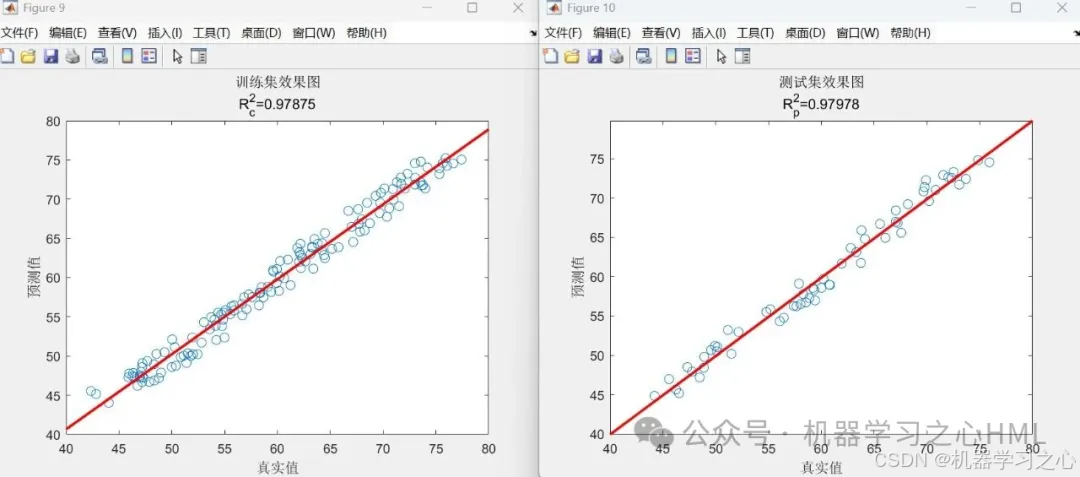
   ? 線性擬合圖
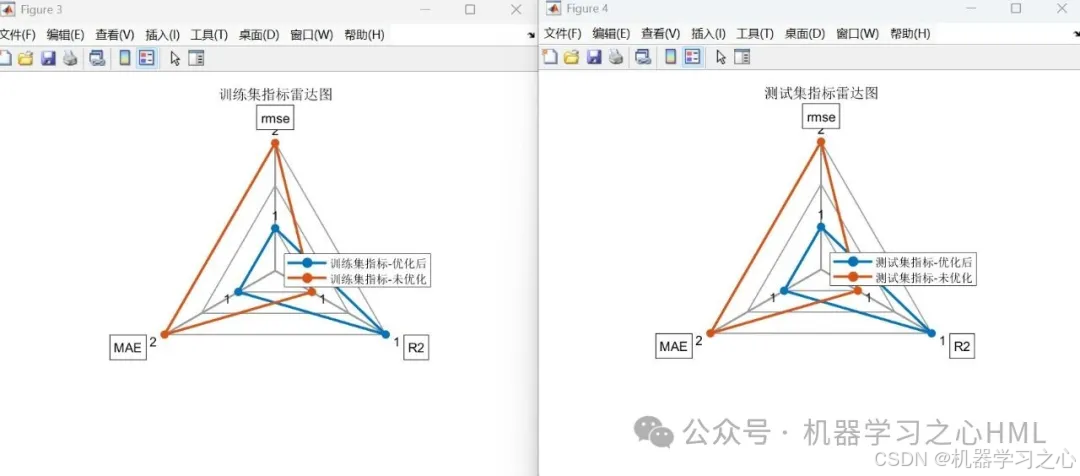
   ? 雷達圖（RMSE/R2/MAE）
6. SHAP特征分析
   ? 基于測試集計算Shapley值
   ? 生成三種可視化：
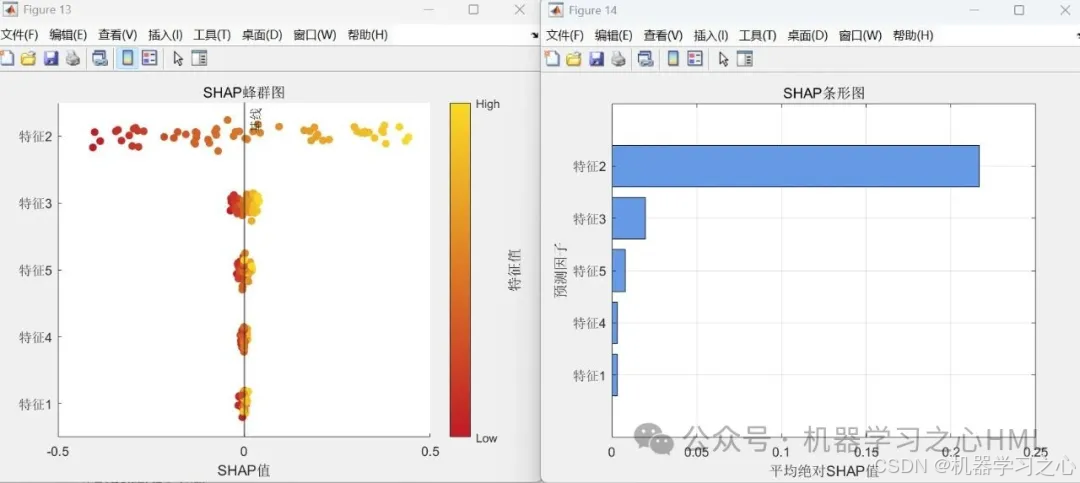
   ? 特征重要性條形圖
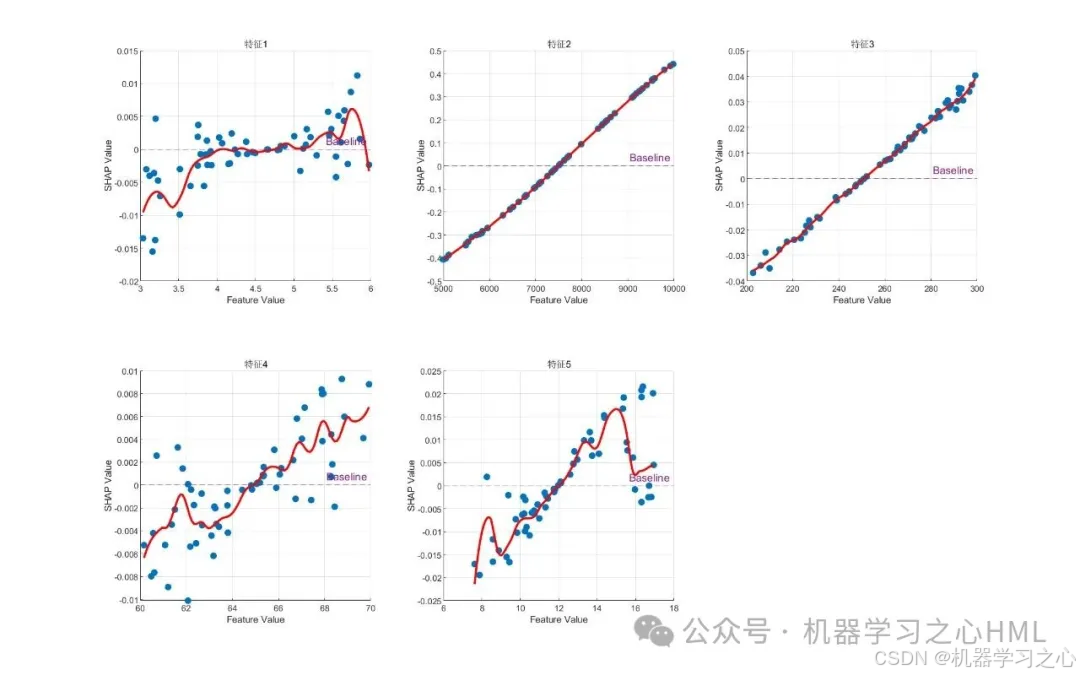
   ? 特征效應散點圖
   ? 摘要圖（特征影響方向）
7. 新數據預測
   ? 加載新的多輸入.xlsx
   ? 自動應用相同歸一化參數
   ? 輸出預測結果到新的輸出.xlsx

技術路線

---

關鍵參數設定

參數	值	說明
ratio	0.7	訓練集占比
N1/N2	10	種群大小
Max_iteration	30	優化算法迭代次數
chaos_label	2	混沌映射類型（Chebyshev）
tf	{‘tansig’,‘purelin’}	隱藏層/輸出層激活函數
epochs	1000	最大訓練輪次
goal	1e-6	訓練目標誤差

---

運行環境要求

1. MATLAB版本：R2020b及以上
2. 必要工具箱：
   • Deep Learning Toolbox
   • Optimization Toolbox
   • Parallel Computing Toolbox（可選，加速SHAP計算）
3. 依賴文件：
   • spider_plot\（雷達圖繪制）
   • 自定義函數
4. 數據格式：Excel文件（特征列+標簽列）

---

應用場景

1. 科研論文：提供完整的優化-評估-解釋流程，可直接生成論文圖表
2. 數模比賽：適用于數學建模比賽的回歸問題
3. 工業預測：如：
   • 設備壽命預測
   • 金融風險評估
   • 銷售量預測
4. 特征工程：通過SHAP分析識別關鍵特征
5. 算法對比：驗證智能優化算法對傳統BP網絡的改進效果

注意：代碼中使用的混沌映射（Chebyshev）可增強優化算法的全局搜索能力，避免早熟收斂。SHAP分析部分需確保特征名稱（featureNames）與實際數據匹配。

部分源碼

X = res(:,1:end-1);  %輸入特征
Y = res(:,end);  %輸出
%計算輸入和輸出維度
inp = size(X,2);  %輸入特征數
put = size(Y,2);  %輸出個數
%%  數據歸一化 索引
X = res(:,1:inp);  %輸入特征
Y = res(:,end-put+1:end);  %輸出
[x,psin]= mapminmax(X', 0, 1);
%保留歸一化后相關參數
[y, psout] = mapminmax(Y', 0, 1);
%%  劃分訓練集和測試集
num = size(res,1);%總樣本數
k = input('是否打亂樣本(是：1，否：0)：');
if k == 0state = 1:num; %不打亂樣本
elsestate = randperm(num); %打亂樣本
end
ratio = 0.7; %訓練集占比
trainnum = floor(num*ratio);
testnum = num-trainnum;
%取出訓練集的x,y
x_train = x(:,state(1: trainnum));
y_train = y(:,state(1: trainnum));
%取出測試集的x,y
x_test = x(:,state(trainnum+1: end));
y_test = y(:,state(trainnum+1: end));
%% 智能優化算法的初始值
% label=1 對應 tent 映射  
% label=2 對應 chebyshev 映射  
% label=3 對應 singer 映射  
% label=4 對應 logistic 映射  
% label=5 對應 sine 映射  
% label=6 對應 circle 映射
% label=7 對應 立方映射
% label=8 對應 Hénon 映射
% label=9 對應廣義Logistic映射
% 如果label不是1-9之間的整數，則默認生成隨機矩陣 
label = 2;  %自行指定
%%  第一步優化隱藏層神經元個數、學習率
%調用算法,兩個變量：x1為神經元個數,x2為學習率
N1=10; %種群數
Max_iteration1 = 30; %迭代次數
%神經元個數范圍,floor(sqrt(inp+put))~10+ceil(sqrt(inp+put))，可以自行改變
%學習率范圍0-0.1，可以自行改變
lb1=[floor(sqrt(inp+put)) 0];%下限值
ub1=[10+ceil(sqrt(inp+put)) 0.1];%上限值
dim1=2; %2個變量，神經元個數、學習率%gbest為最優參數（對應誤差最小情況時神經元、學習率）
besthiddens = round(gBest1(1));
bestlearn = gBest1(2);
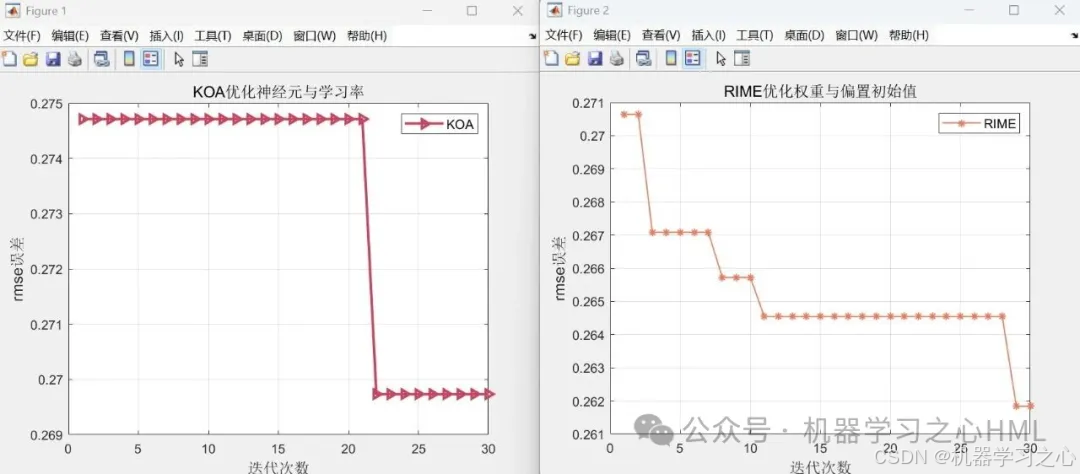
%迭代曲線1
figure
plot(cg_curve1,'->','LineWidth',2,Color=[200,68,94]./255)
% 添加圖例，并設置字體大小  % 設置 x 軸和 y 軸的標簽，并設置字體大小  
xlabel('迭代次數','FontSize',12); 
ylabel('rmse誤差','FontSize',12);% 顯示網格（可選）  
grid on; 
%%  第二步優化權重、偏置初始值N2=10; %種群數
Max_iteration2 = 30; %迭代次數
%神經元個數范圍,floor(sqrt(inp+put))~10+ceil(sqrt(inp+put))，可以自行改變
%學習率范圍0-0.1，可以自行改變
lb2=-1;%下限值
ub2=1;%上限值
dim2=inp * besthiddens + besthiddens + besthiddens * put + put; %變量個數
[gBestScore2,gBest2,cg_curve2]=PSO(N2,Max_iteration2,lb2,ub2,dim2,fitness2,label);
%迭代曲線2
figure
plot(cg_curve2,'-*','LineWidth',1,Color=[233,122,94]./255)
% 添加圖例，并設置字體大小  % 設置 x 軸和 y 軸的標簽，并設置字體大小  
xlabel('迭代次數','FontSize',12); 
ylabel('rmse誤差','FontSize',12);% 顯示網格（可選）  
grid on; 

數據集

數據集（訓練和測試數據）

數據集（新數據輸入）

代碼獲取私信回復SHAP分析+KOA-RIME開普勒結合霜冰算法雙重優化BP神經網絡+9種映射方法+新數據預測！機器學習可解釋分析！