假設檢驗的原理

假設檢驗是統計學中用于判斷樣本數據是否支持某個特定假設的方法。其核心思想是通過樣本數據對總體參數或分布提出假設，并利用統計量來判斷這些假設的合理性。假設檢驗的基本步驟如下：

1. 假設（Hypothesis）

在統計學中，假設是指對總體參數（如均值、方差、比例等）或數據分布的一種猜測或主張。

例如：

“某新藥比舊藥更有效”（即新藥組的均值療效 > 舊藥組的均值療效）。
“男性和女性的工資水平無差異”（即兩組的工資均值相等）。

假設通常分為：

原假設（Null Hypothesis, H?）：默認成立的假設，通常表示“無效果”、“無差異”或“無關系”。

例如：H?: μ = 100（總體均值等于100）。

備擇假設（Alternative Hypothesis, H?）：與原假設對立，表示“有效果”、“有差異”或“有關系”。

例如：H?: μ ≠ 100（雙側檢驗）、H?: μ > 100（單側右尾檢驗）、H?: μ < 100（單側左尾檢驗）。

2. 假設檢驗（Hypothesis Testing）

假設檢驗是一種統計方法，用于判斷樣本數據是否支持原假設，或者是否有足夠證據拒絕原假設而支持備擇假設。

核心思想：
- 先假設 H? 為真，然后計算在當前假設下觀察到樣本數據的概率（P值）。
- 如果這個概率很小（通常 ≤ 0.05），則拒絕 H?，認為 H? 更可信。

如何提出假設？

提出假設是假設檢驗的第一步，需要結合研究問題和數據特性。以下是具體方法：

1. 明確研究問題

先確定你要驗證的核心問題。例如：

“新教學方法是否提高了學生成績？”
“A品牌電池的續航時間是否比B品牌長？”
“吸煙是否與肺癌發病率相關？”

2. 確定檢驗類型

參數檢驗（適用于已知分布的總體參數，如均值、方差）：

例如：t檢驗（均值）、Z檢驗（比例）、F檢驗（方差）等。

非參數檢驗（適用于未知分布或非數值數據）：

例如：Mann-Whitney U檢驗（比較兩組中位數）、卡方檢驗（分類變量獨立性）等。

3. 設定原假設（H?）和備擇假設（H?）

H? 通常是“無差異”或“無影響”的保守假設，例如：

“新舊教學方法無差異”（H?: μ? = μ?）。
“A品牌和B品牌電池續航時間相同”（H?: μ_A = μ_B）。

H? 取決于研究目標，可以是：

雙側檢驗（Two-tailed）：只關心“是否有差異”，不關心方向。

例如：H?: μ? ≠ μ?

單側檢驗（One-tailed）：關心“是否更大/更小”。

例如：H?: μ? > μ?（新方法更好）或 H?: μ_A < μ_B（A品牌更差）

4. 選擇顯著性水平（α）

通常 α = 0.05（5%），表示允許犯第一類錯誤（錯誤拒絕H?）的概率為5%。
如果研究要求更嚴格（如醫學試驗），可以選 α = 0.01。

舉例說明

例1：檢驗新藥是否比舊藥更有效

假設：

H?: μ_新 ≤ μ_舊（新藥不比舊藥更好）
H?: μ_新 > μ_舊（新藥更有效，單側右尾檢驗）

檢驗方法：獨立樣本 t 檢驗（比較兩組均值）。

例2：檢驗某班級的平均成績是否為75分

研究問題：班級平均分是否 ≠ 75？

假設：
- H?: μ = 75（班級平均分等于75）
- H?: μ ≠ 75（班級平均分不等于75，雙側檢驗）

檢驗方法：單樣本 t 檢驗。

例3：檢驗性別是否影響工資水平

研究問題：男女工資均值是否不同？

假設：
- H?: μ_男 = μ_女（性別不影響工資）
- H?: μ_男 ≠ μ_女（性別影響工資，雙側檢驗）

檢驗方法：獨立樣本 t 檢驗或 Mann-Whitney U 檢驗（若數據非正態）。

總結

假設是對總體參數的猜測，分為原假設（H?）和備擇假設（H?）。
假設檢驗是通過統計方法判斷是否拒絕H?。
如何提出假設：
- 明確研究問題 → 選擇檢驗類型 → 設定H?和H? → 選擇α。
關鍵點：
- H?通常是“無差異”的保守假設。
- H?可以是雙側（≠）或單側（> 或 <）。
- α通常取0.05，但可根據研究調整。

至于什么是單側檢驗什么是雙側檢驗呢?

假設檢驗的方向性決定了你是用單側檢驗（One-tailed Test）還是雙側檢驗（Two-tailed Test）。它們的核心區別在于：

比較項	單側檢驗	雙側檢驗
研究問題	只關心“是否更大”或“是否更小”	只關心“是否有差異”（不關心方向）
備擇假設（H?）	H?: μ > μ?（右尾）或 μ < μ?（左尾）	H?: μ ≠ μ?
拒絕域	僅分布在統計量的一側（左或右）	分布在統計量的兩側（左和右）
適用場景	有明確方向性的預測（如“新藥更好”）	無方向性，只檢驗差異（如“新舊藥不同”）?

1. 雙側檢驗（Two-tailed Test）

核心思想：只關心“有沒有差異”，不關心是“正差異”還是“負差異”。

備擇假設（H?）：μ ≠ μ?（可以是更大或更小）。

拒絕域：分布在統計量的左右兩側（例如，|Z| > 1.96）。

舉例：

問題：某工廠生產的零件長度標準是10cm，現在懷疑機器有問題，但不確定是偏長還是偏短。

假設：

假設：
- H?: μ = 10cm（機器正常）
- H?: μ ≠ 10cm（機器異常，可能偏長或偏短）
檢驗方法：計算樣本均值，如果顯著大于或小于10cm，都拒絕H?。

2. 單側檢驗（One-tailed Test）

核心思想：明確關心“是否更大”或“是否更小”。

拒絕域：僅分布在統計量的一側（例如，Z > 1.645 或 Z < -1.645）。

舉例：
- 問題1（右尾）：某新藥聲稱比舊藥更有效，需驗證是否真的“更有效”。
  - H?: μ_新 ≤ μ_舊
  - H?: μ_新 > μ_舊
  - 只有新藥顯著更好時，才拒絕H?。
- 問題2（左尾）：某減肥廣告聲稱“平均減重≥5kg”，消費者懷疑夸大效果。
  - H?: μ ≥ 5kg
  - H?: μ < 5kg
  - 只有實際減重顯著小于5kg時，才拒絕H?。

雙側檢驗拒絕域：     單側檢驗（右尾）拒絕域：／＼                ／|/    \              /  |/      \            /   |
[拒絕域][拒絕域]    [接受域][拒絕域]

如何選擇單側 or 雙側？

用雙側檢驗的情況：
- 研究問題只是“是否有差異”，無方向性預測。
- 例如：“男女身高是否不同？”（可能男高或女高）。
用單側檢驗的情況：
- 研究問題有明確方向（如“新方法更好”“新藥更差”）。
- 例如：“新教學方法是否提高了成績？”（只需檢驗是否>）。

注意事項

單側檢驗更容易顯著（因為拒絕域集中在一側，統計量更容易達標），但必須提前確定方向，不能看到數據后再選方向（否則是學術不端）。
雙側檢驗更保守（需要更強的證據才能拒絕H?），適用于探索性研究。

舉個例子

問題：某飲料標稱容量為500ml，質檢部門想檢測是否達標。

如果只是懷疑容量可能不準確（可能多或少）：
- 用雙側檢驗：H?: μ ≠ 500ml
如果廠商聲稱“容量≥500ml”，消費者懷疑不足：
- 用單側（左尾）檢驗：H?: μ < 500ml

拒絕域（Rejection Region）和接受域（Acceptance Region）是假設檢驗中用于判斷是否拒絕原假設（H?）的統計量范圍。它們的劃分基于顯著性水平（α）和統計量的分布。

1. 拒絕域（Rejection Region）

定義：如果檢驗統計量（如Z值、t值）落在這一區域，就拒絕H?，認為備擇假設（H?）更可信。

特點：
- 位于統計量分布的極端區域（尾部）。
- 范圍由顯著性水平（α）決定（如α=0.05時，拒絕域占分布的5%）。

舉例：
- 在正態分布中，若α=0.05（雙側檢驗），拒絕域是Z < -1.96 或 Z > 1.96。

2. 接受域（Acceptance Region）

定義：如果檢驗統計量落在這一區域，就不拒絕H?（注意：不是“接受H?”，而是“沒有足夠證據拒絕”）。

特點：
- 位于統計量分布的中間區域。
- 范圍是1-α（如α=0.05時，接受域占95%）。

舉例：
- 在正態分布中，若α=0.05（雙側檢驗），接受域是 -1.96 ≤ Z ≤ 1.96。

如何確定拒絕域和接受域？

步驟1：明確檢驗類型（單側/雙側）

雙側檢驗（H?: μ ≠ μ?）：拒絕域在分布的兩側。
- 例如：α=0.05時，每側占2.5%（Z=±1.96）。
單側檢驗（H?: μ > μ? 或 μ < μ?）：拒絕域在分布的一側。
- 例如：α=0.05時，右尾檢驗的臨界值為Z=1.645。

步驟2：根據分布和α查臨界值

Z檢驗（正態分布）：查Z表。
t檢驗（t分布）：查t表（需考慮自由度）。
其他分布：如χ2分布、F分布等。

步驟3：畫出分布圖并標記區域

雙側檢驗示例（α=0.05）：

拒絕域      接受域      拒絕域
Z < -1.96   -1.96 ≤ Z ≤ 1.96   Z > 1.96

單側右尾檢驗示例（α=0.05）：

接受域         拒絕域
Z ≤ 1.645      Z > 1.645

實際案例說明

案例1：單樣本Z檢驗（雙側）

問題：檢驗某批次燈泡壽命均值是否為1000小時（H?: μ=1000，H?: μ≠1000，α=0.05）。
步驟：
1. 計算樣本均值（如x?=1020），標準差（σ=50），n=30。
2. 計算Z值：

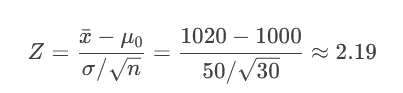
?xˉ?μ0??=50/30

?1020?1000?≈2.19
查Z表得臨界值：±1.96。
決策：
- Z=2.19 > 1.96 → 落在拒絕域 → 拒絕H?。

案例2：單側t檢驗（左尾）

問題：檢驗某減肥藥平均減重是否<5kg（H?: μ≥5，H?: μ<5，α=0.05）。
步驟：
1. 計算樣本均值（x?=4.2），標準差（s=1.2），n=25。
2. 計算t值（自由度=24）：

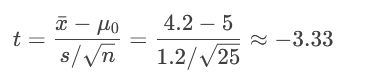
查t表得臨界值（左尾）：t=-1.711。
決策：
- t=-3.33 < -1.711 → 落在拒絕域 → 拒絕H?。

關鍵注意事項

接受域 ≠ 證明H?為真：
- 不拒絕H?只能說明“證據不足”，不能直接得出“H?正確”的結論。
單側檢驗更敏感：
- 同樣的α下，單側檢驗的臨界值更寬松（如Z=1.645 vs 雙側的1.96），更容易拒絕H?。
P值與拒絕域的關系：
- P值 < α → 檢驗統計量落在拒絕域內。

總結

拒絕域：統計量的極端值區域，拒絕H?。
接受域：統計量的中間值區域，不拒絕H?。
如何確定：
1. 選擇單側/雙側檢驗。
2. 根據α和分布查臨界值。
3. 比較統計量與臨界值，判斷是否落在拒絕域。

如何用統計量做出決策？

在假設檢驗中，“用統計量決策”是指通過計算樣本數據的統計量（如Z值、t值、F值等），并將其與預先設定的臨界值或P值進行比較，從而決定是否拒絕原假設（H?）。以下是具體步驟和邏輯：

1. 統計量決策的核心邏輯

假設檢驗的決策基于以下兩種等價方法：

臨界值法（拒絕域法）：比較統計量與臨界值。
P值法：比較P值與顯著性水平（α）。

最終結論一致，只是判斷方式不同。

2. 統計量決策的步驟

步驟1：計算檢驗統計量

根據數據類型和假設檢驗類型，選擇合適的統計量公式。例如：

Z檢驗（總體方差已知或大樣本）：

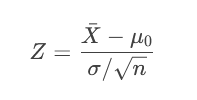
t檢驗（總體方差未知且小樣本）：

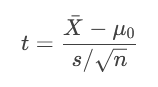
卡方檢驗（分類數據或方差檢驗）：

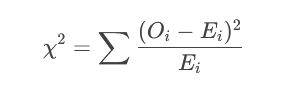
步驟2：確定拒絕域（臨界值法）

根據顯著性水平（α）和檢驗類型（單側/雙側），查統計分布表（Z表、t表等）找到臨界值。
- 雙側檢驗：拒絕域在兩側（如α=0.05時，Z=±1.96）。
- 單側檢驗：拒絕域在一側（如α=0.05右尾檢驗，Z=1.645）。

決策規則：

如果統計量 > 臨界值（或 < -臨界值） → 拒絕H?。

否則 → 不拒絕H?。

示例（Z檢驗，雙側α=0.05）

計算得Z=2.1，臨界值=±1.96。
2.1 > 1.96 → 拒絕H?。

步驟3：P值法（更常用的現代方法）

P值是在原假設H?為真的情況下，觀察到當前統計量或更極端值的概率。

P值 ≤ α → 拒絕H?。
P值 > α → 不拒絕H?。

如何計算P值？

Z檢驗：P值 = P(Z ≥ |統計量|) × 2（雙側）或 P(Z ≥ 統計量)（單側）。
t檢驗：查t分布表或軟件計算。

示例（t檢驗，單側α=0.05）

計算得t=2.3，自由度=20，查表得P≈0.016。
0.016 < 0.05 → 拒絕H?。

3. 實際案例

案例1：Z檢驗（比較均值）

問題：某工廠生產零件，標準長度μ?=10cm。質檢員抽樣30個零件，測得平均長度Xˉ=10.2cmXˉ=10.2cm，總體標準差σ=0.5cm。問零件是否符合標準？（α=0.05）

步驟：

假設：
- H?: μ = 10cm
- H?: μ ≠ 10cm（雙側檢驗）

2.計算Z值：

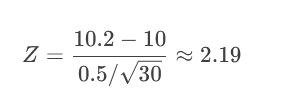
查臨界值（α=0.05雙側）：Z=±1.96。
決策：
- 2.19 > 1.96 → 拒絕H?（零件長度不符合標準）。

P值法：

P(Z ≥ 2.19) ≈ 0.014（單側），雙側P≈0.028。
0.028 < 0.05 → 拒絕H?。

案例2：t檢驗（單側）

問題：某減肥藥聲稱平均減重≥5kg。消費者協會抽樣25人，測得平均減重Xˉ=4.3kgXˉ=4.3kg，樣本標準差s=1.2kg。檢驗廣告是否虛假？（α=0.05）

步驟：

假設：
- H?: μ ≥ 5kg
- H?: μ < 5kg（左尾檢驗）

計算t值：

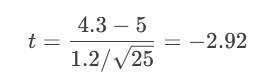
查臨界值（α=0.05，自由度=24）：t=-1.711。
決策：
- -2.92 < -1.711 → 拒絕H?（廣告可能虛假）。

P值法：

P(t ≤ -2.92) ≈ 0.004。
0.004 < 0.05 → 拒絕H?。

4. 總結：統計量決策的核心

計算統計量（Z/t/χ2等）反映樣本與H?的偏離程度。
比較統計量與臨界值，或 比較P值與α。
決策：
- 如果統計量落入拒絕域（或P≤α）→ 拒絕H?。
- 否則 → 不拒絕H?。

關鍵點：

臨界值法適合手工計算，P值法更精確（軟件常用）。
不拒絕H? ≠ 證明H?為真，只是證據不足。
單側檢驗更敏感（更容易拒絕H?），但需提前確定方向。

如何用P值進行假設檢驗決策？

P值是假設檢驗中最常用的決策工具之一，它比臨界值法更直接，尤其適用于統計軟件（如Python、R、SPSS）的分析結果。以下是P值決策的完整步驟和邏輯：

1. P值的定義

P值（P-value）表示：
“在原假設H?為真的情況下，觀察到當前樣本數據（或更極端情況）的概率。”
- 如果P值很小（比如≤0.05），說明當前數據在H?下極不可能發生，因此拒絕H?。
- 如果P值較大（比如>0.05），說明數據與H?一致，沒有足夠證據拒絕H?。

2. P值決策的步驟

步驟1：設定假設和顯著性水平（α）

原假設（H?）：如 μ = 100
備擇假設（H?）：如 μ ≠ 100（雙側）或 μ > 100（單側）
顯著性水平（α）：通常取 0.05（5%）。

步驟2：計算檢驗統計量

根據數據類型選擇統計量（如Z值、t值、卡方值等）：

Z檢驗（總體方差已知）：

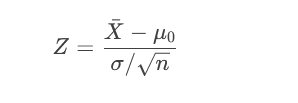
t檢驗（總體方差未知）：

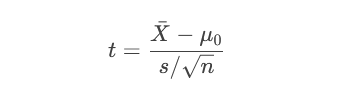
步驟3：計算P值

根據統計量和檢驗類型計算P值：

雙側檢驗：P = 2 × P(統計量 ≥ |當前值|)
（例如Z=2.0 → P = 2 × P(Z ≥ 2.0) ≈ 0.0455）
單側檢驗：
- 右尾檢驗：P = P(統計量 ≥ 當前值)
- 左尾檢驗：P = P(統計量 ≤ 當前值)

注：實際中通常用統計軟件（如Python的scipy.stats）直接計算P值，無需手動查表。

步驟4：比較P值與α

如果 P ≤ α → 拒絕H?，認為結果顯著。
如果 P > α → 不拒絕H?，認為結果不顯著。

3. 實際案例

案例1：Z檢驗（雙側）

問題：某飲料標稱容量500ml，質檢抽檢50瓶，測得平均容量498ml，總體標準差10ml。檢驗是否達標（α=0.05）。

步驟：

假設：
- H?: μ = 500ml
- H?: μ ≠ 500ml（雙側）

2.計算Z值：

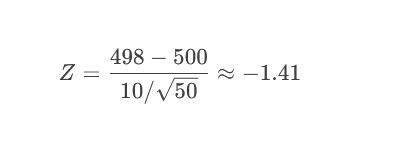
計算P值（雙側）：
- P = 2 × P(Z ≤ -1.41) ≈ 2 × 0.079 = 0.158
決策：
- 0.158 > 0.05 → 不拒絕H?（容量達標）。

案例2：t檢驗（單側左尾）

問題：某減肥藥廣告稱“平均減重≥5kg”，消費者抽檢20人，測得平均減重4.2kg，標準差1.5kg。檢驗廣告是否虛假（α=0.05）。

步驟：

假設：
- H?: μ ≥ 5kg
- H?: μ < 5kg（左尾）

2.計算t值（自由度=19）：

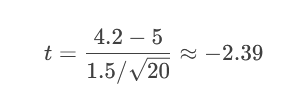
3.計算P值（左尾）：

P = P(t ≤ -2.39) ≈ 0.013

4.決策

0.013 < 0.05 → 拒絕H?（廣告可能虛假）。

4. P值 vs 臨界值法

對比項	P值法	臨界值法
核心邏輯	直接計算“極端概率”	比較統計量與臨界值
適用場景	軟件分析、精確計算	手工計算、理論推導
結果一致性	與臨界值法結論相同	與P值法結論相同
優勢	更直觀（直接顯示顯著性）	適合考試或理論教學

5. 注意事項

P值 ≠ H?為真的概率：
- P值是基于H?為真的假設計算的，不能理解為“H?正確的概率”。
不要混淆單側/雙側P值：
- 單側檢驗的P值通常是雙側的一半（如Z=1.96，單側P=0.025，雙側P=0.05）。
P值接近α時謹慎結論：
- 如P=0.06（α=0.05），雖不顯著，但可能是樣本量不足導致的。

6. 總結

P值決策規則：
- P ≤ α → 拒絕H?（結果顯著）。
- P > α → 不拒絕H?（結果不顯著）。
P值的意義：
- 越小越反對H?，越大越支持H?的合理性。

P值決策與統計量決策的比較

核心關系：一一對應

首先要理解最根本的一點：對于一個給定的檢驗，其計算出的統計量（如t值、Z值）都對應著一個唯一的P值。

統計量：是一個絕對數值，表示你的樣本數據與H?的偏離程度（例如，t = 2.5）。偏離程度越大，統計量的絕對值越大。
P值：是一個概率，表示在H?成立的前提下，出現當前統計量（或更極端情況）的可能性（例如，P = 0.012）。這個可能性越小，P值越小。

它們通過統計分布（如t分布、正態分布）緊密相連。一個較大的統計量絕對值（如 |t| = 2.5）必然對應一個較小的P值（如 P = 0.012）。

對比表格

對比維度	統計量決策（臨界值法）	P值決策（P-value法）
決策依據	將計算出的檢驗統計量（t, Z, F）與臨界值（來自分布表）進行比較。	將計算出的P值與顯著性水平α（如0.05）進行比較。
決策規則	如果	統計量	>	臨界值	，則拒絕H?。	如果 P值 ≤ α，則拒絕H?。
決策規則	如果	統計量	>	臨界值	（統計量落入拒絕域）	如果 P值 ≤ α，則拒絕H?。
輸出結果	一個數值（如 t = 2.19）	一個概率（如 P = 0.031）
信息量	較少。只知道是否顯著，不知道“有多顯著”。	更豐富。不僅知道是否顯著，還能知道在多大程度上顯著（P值越小，拒絕H?的證據越強）。
直觀性	較抽象，需要理解分布和拒絕域的概念。	更直觀。P值直接反映了結果的反常程度。
適用場景	手工計算、考試、理論推導。	現代統計分析的主流，幾乎所有統計軟件（R, Python, SPSS等）默認報告P值。
靈活性	固定。α一旦確定，臨界值就固定了。	更靈活。可以直接看到P值是0.049還是0.001，從而判斷證據的強度。而臨界值法只知道“過了線”。

一個比喻：考試及格線

統計量決策：就像你的考試原始分數是85分（統計量），及格線是60分（臨界值）。85 > 60，所以你及格了（拒絕H?）。但你不知道85分在班里到底處于什么水平。
P值決策：就像告訴你，你的分數超過了97%的同學（P值=0.03）。學校的政策是超過95%的同學算優秀（α=0.05）。因為你超過了97% > 95%，所以你被評為優秀（拒絕H?）。它不僅告訴了你結果，還告訴了你卓越的程度。

實際案例對比

問題：檢驗某班級平均分數是否為75分（雙側檢驗，α=0.05）。

樣本數據：n=30, x?=78, s=10
計算出的統計量：t ≈ 1.64 (自由度df=29)

1. 統計量決策（臨界值法）

查t分布表（df=29, α=0.05 雙側），找到臨界值 t* = ±2.045。
比較：|1.64| < 2.045
決策：統計量未落入拒絕域，因此不拒絕H?。

2. P值決策

計算t=1.64對應的P值（使用軟件或更精確的表）。對于雙側檢驗，P值 = 2 * P(T > 1.64) ≈ 0.112。
比較：P值 (0.112) > α (0.05)
決策：不拒絕H?。

結論

兩種方法得出的結論完全相同：沒有足夠證據拒絕“平均分是75分”的原假設。

但P值提供了更多信息：P=0.112 意味著，即使H?成立，也有11.2%的概率會觀察到這樣的樣本結果。這個概率遠大于5%，所以我們認為這個結果并不反常，不足以推翻H?。

總結與選擇

特性	統計量決策	P值決策	勝出方
結論一致性	完全相同	完全相同	平手
信息豐富度	低	高	P值法
直觀性	低	高	P值法
現代應用	少	多（軟件標準）	P值法
理論理解	有助于理解分布和拒絕域	更結果導向	統計量法

對于學習者：理解統計量決策有助于夯實假設檢驗的理論基礎，明白決策的整個過程。
對于實踐者：P值決策是毫無疑問的首選。它由軟件自動計算，提供的信息更豐富，解讀更直接。在報告結果時，應同時提供統計量、自由度、P值等信息（例如，t(29) = 1.64, p = .112），而不僅僅是“顯著”或“不顯著”。

簡單來說，P值決策是統計量決策的一種更高級、信息更全面的呈現方式。

怎么表述決策結果——不拒絕而不是接受

為什么是“不拒絕”而不是“接受”？

這背后的核心思想是 “無罪推定” 原則。

原假設（H?）是默認的“無罪”狀態。我們一開始就假定它是成立的，就像法庭上假定被告無罪。
檢驗的目的是尋找足以推翻這個假設的強有力證據（樣本數據），就像檢察官尋找能證明被告有罪的證據。
“拒絕H?”：意味著我們找到了足夠強的證據（P值很小），因此我們可以推翻最初的“無罪”設定，判定“有罪”。這是一個積極的、確定的結論。
“不拒絕H?”：意味著我們找到的證據不足以推翻“無罪”的設定。但這不等于證明了“無罪”。可能的原因有兩種：
- H?確實為真。
- H?為假，但我們的證據太弱（比如樣本太小、數據變異太大），沒能檢測出來。

“接受”意味著你肯定了H?的正確性，而假設檢驗從未證明H?為真，它只是說明當前數據沒有提供反對H?的證據。

決策	錯誤（不嚴謹）的表述	正確（嚴謹）的表述
拒絕 H?	“我們接受備擇假設H?。”	“在α=0.05的水平上，有足夠的統計證據拒絕原假設H?。”
	“我們證明了H?。”	“數據支持備擇假設H?。”
		“結果表明，差異具有統計學意義。”
不拒絕 H?	“我們接受原假設H?。”	“在α=0.05的水平上，沒有足夠的統計證據拒絕原假設H?。”
	“我們證明了H?。”	“本次分析未能發現 statistically significant 的證據支持H?。”
		“數據與原假設H?一致。”

實際案例中的表述

案例1：拒絕H?（新藥有效性的t檢驗）

研究問題：新藥是否比安慰劑更有效？
H?: μ_新藥 ≤ μ_安慰劑（無效）
H?: μ_新藥 > μ_安慰劑（有效）
結果: t(58) = 2.85, p = 0.003

錯誤表述：

“我們接受了新藥更有效的假設。”

正確表述：

“拒絕原假設。在α=0.05的水平上，統計分析提供了足夠的證據（t(58)=2.85, p=0.003）表明新藥的治療效果顯著優于安慰劑。”

案例2：不拒絕H?（零件質量的Z檢驗）

研究問題：生產線生產的零件長度是否是10cm？
H?: μ = 10 cm （合格）
H?: μ ≠ 10 cm （不合格）
結果: Z = 1.20, p = 0.230

錯誤表述：

“我們得出結論，零件平均長度就是10cm。”

正確表述：

“未能拒絕原假設。在α=0.05的水平上，沒有足夠的統計證據（Z=1.20, p=0.230）表明零件的平均長度與10cm有統計學上的顯著差異。當前數據與生產線運行正常的假設是一致的。”

更進一步的解釋（推薦）：

“……未能發現顯著差異。但這不能斷定零件長度** exactly **是10cm，可能存在的微小差異由于本次樣本量有限而未被檢測到。建議持續監控或擴大樣本量進行進一步驗證。”

總結：如何記住并應用

記住法庭比喻：不說“接受無罪”，只說“證據不足，無法定罪”或“證據確鑿，認定有罪”。
報告結果時，始終將統計量、P值和決策一起報告。
- 格式：(統計量(自由度)=數值, p=數值)
- 例如：(t(25) = 2.11, p = .045) 或 (χ2(1) = 5.68, p = .017)
使用標準短語：
- 拒絕H?時：“有足夠證據拒絕H?”、“結果顯著”。
- 不拒絕H?時：“沒有足夠證據拒絕H?”、“未發現顯著差異”、“數據與H?一致”。

怎么樣表述決策結果——“顯著”或“不顯著”

核心原則

永遠不要只說“顯著”或“不顯著”：必須說明是在什么顯著性水平（α） 下做出的判斷。例如，“在0.05水平上顯著”。
提供統計證據：必須報告計算出的檢驗統計量（如 t值、χ2值、F值）和 P值。這是結論的支撐。
區分“統計顯著”與“實際顯著”：一個結果可能具有統計顯著性（即不太可能是偶然發生的），但效應量非常小，在實際業務或科學場景中沒有實際意義。
對“不顯著”的結果保持謙遜：不說“接受原假設”或“證明沒有差異”，而說“未能發現顯著差異”或“證據不足以拒絕原假設”。

如何表述“顯著”的結果

當 P值 ≤ α 時，我們拒絕原假設（H?），結果是顯著的。

表述結構：結論 + 統計證據 + 上下文含義。

常用話術：

“……之間存在統計學上顯著的差異。”
“……對……有顯著影響。”
“數據提供了充分的證據表明……”
“我們拒絕原假設，支持……”

舉例（假設 α = 0.05）：

T檢驗： “獨立樣本t檢驗顯示，使用新教學方法的學生成績（M=85, SD=4）顯著高于使用傳統方法的學生（M=80, SD=5），*t*(58) = 3.85, *p* = .002。”
卡方檢驗： “不同性別與產品偏好之間存在顯著關聯，χ2(2, N = 200) = 10.52, *p* = .005。”
回歸分析： “回歸分析表明，每日鍛煉時間對減肥效果有顯著的正向預測作用，β = .45, *t*(98) = 5.11, *p* < .001。”

如何表述“不顯著”的結果

當 P值 > α 時，我們未能拒絕原假設（H?），結果是不顯著的。

表述結構：謹慎結論 + 統計證據 + 可能原因或局限性（可選）。

常用話術：

“……之間的差異無統計學意義。”
“未能發現……對……有顯著影響。”
“數據沒有提供足夠的證據表明……”
“結果不支持備擇假設……”
“在本次研究中，……與……沒有顯著關聯。”

舉例（假設 α = 0.05）：

T檢驗： “獨立樣本t檢驗發現，A組（M=52, SD=11）與B組（M=55, SD=10）的平均得分差異無統計學意義，*t*(45) = 1.21, *p* = .233。”
更嚴謹的表述： “……*p* = .233，因此未能拒絕兩組均值相等的原假設。該結果可能表明真正差異很小，也可能由于樣本量不足導致檢驗效力（Power）較低，未能檢測到存在的差異。”
回歸分析： “回歸模型顯示，受教育年限對起始工資的預測作用不顯著，β = .08, *t*(103) = 0.87, *p* = .387。”

表述模板

你可以直接套用以下模板來組織你的語言：

對于“顯著”結果：

【統計方法】表明，【自變量/分組變量】對【因變量/結果變量】有【顯著/顯著的正面/顯著的負面】影響/差異（統計量(自由度) = 值, *p* = P值）。具體來說，【用簡單語言描述發現，例如：A組的平均值比B組高X個單位】。

對于“不顯著”結果：

【統計方法】結果顯示，【自變量/分組變量】與【因變量/結果變量】之間未發現顯著的關聯/差異（統計量(自由度) = 值, *p* = P值）。這意味著當前數據不足以支持【你的研究假設】。

常見錯誤與陷阱

混淆“統計顯著”和“實際重要”：
- 錯誤：“新的網頁設計使點擊率顯著提升了0.1%（p<0.05），因此我們應該立刻投入百萬資金全面推廣。”
- 正確：“雖然新設計帶來了統計上顯著的提升（p<0.05），但0.1%的效應量過小，可能不具備商業價值。建議進行更大規模的測試以評估其實際影響。”
將“不顯著”等同于“沒有效果”：
- 錯誤：“我們的實驗證明，獎金對員工 productivity 沒有影響（p=0.07）。”
- 正確：“在本研究條件下，未能發現獎金對 productivity 有統計上的顯著影響（p=0.07）。但p值接近0.05，提示可能存在一個我們因樣本量限制而未能捕捉到的真實效應，值得進一步研究。”
忽略報告效應量（Effect Size）：
在報告p值的同時，最好也報告效應量（如Cohen's d, η2, R2），這能幫助讀者理解顯著差異的“幅度”有多大。

總結一下：專業的表述是 “結論 + 統計量 + p值” 的組合。對顯著結果，可以自信地解釋；對不顯著結果，務必保持謹慎，并考慮其可能的原因。這樣做才能使你的分析結論顯得嚴謹、可信。

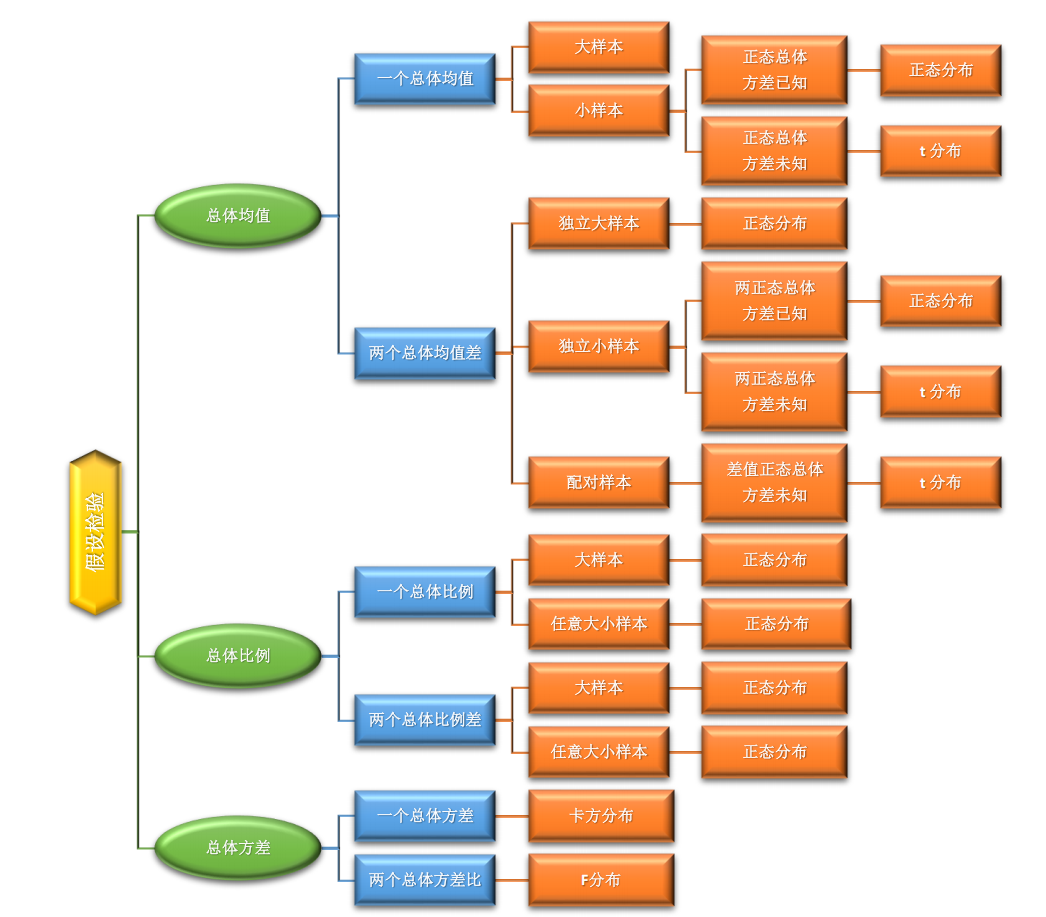
假設檢驗的7個標準步驟

第1步：提出假設

明確原假設和備擇假設。
原假設：
備擇假設：

示例：檢驗一種新減肥藥是否有效（已知有效標準是平均減重 > 5kg）。

H?: μ ≤ 5 kg （新藥無效或不比標準好）
H?: μ > 5 kg （新藥有效）

第2步：選擇顯著性水平

確定第一類錯誤的概率。
常用選擇：。

示例：我們選擇 α = 0.05。這意味著我們有5%的風險錯誤地拒絕一個 actually 為真的H?（即誤判藥有效）。

第3步：確定檢驗統計量及其分布

根據：數據類型、樣本量、總體信息。
常見選擇：
- ：總體方差已知，或大樣本。
- ：總體方差未知，小樣本。
- ：檢驗方差或擬合優度。
- ：比較兩個方差。

示例：我們不知道總體方差，且樣本量較小（n=25），所以使用 t檢驗。檢驗統計量為 t 統計量，服從自由度為 24 的 t 分布。

第4步：制定決策規則

確定拒絕域：根據顯著性水平α和備擇假設H?的方向，查相應的分布表，找到臨界值。
決策規則：如果檢驗統計量落在拒絕域，則拒絕H?。

示例：這是一個右尾檢驗。查 t 分布表（α=0.05, df=24），得到臨界值 **t* = 1.711**。

決策規則：如果計算出的 t > 1.711，就拒絕H?。

第5步：收集數據并計算檢驗統計量

從總體中抽取一個隨機樣本。
根據樣本數據計算檢驗統計量的實際值。

示例：隨機抽取25名被試者。計算得樣本平均減重 xˉ=5.8xˉ=5.8 kg，樣本標準差 s=1.5s=1.5 kg。
計算 t 統計量：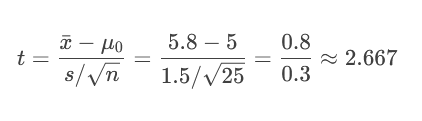

第6步：做出統計決策

將第5步計算出的統計量與第4步制定的決策規則進行比較。
兩種等價方法：
1. 臨界值法：t = 2.667 > 1.711 → 統計量落入拒絕域。
2. P值法：計算P值（P(t > 2.667) ≈ 0.007）。由于 0.007 < 0.05 (α) → P值小于α。

決策：拒絕原假設H?。

第7步：給出統計結論

用非技術性語言陳述決策結果，并結合問題背景進行解釋。
切記：對“不拒絕H?”的情況，不要說“接受H?”。

示例：

統計結論：在0.05的顯著性水平上，有足夠的統計證據拒絕原假設。
現實意義結論：數據分析表明，該新減肥藥的平均減重效果顯著高于5kg的標準，具有統計學意義。這意味著我們有足夠的信心認為該藥是有效的。

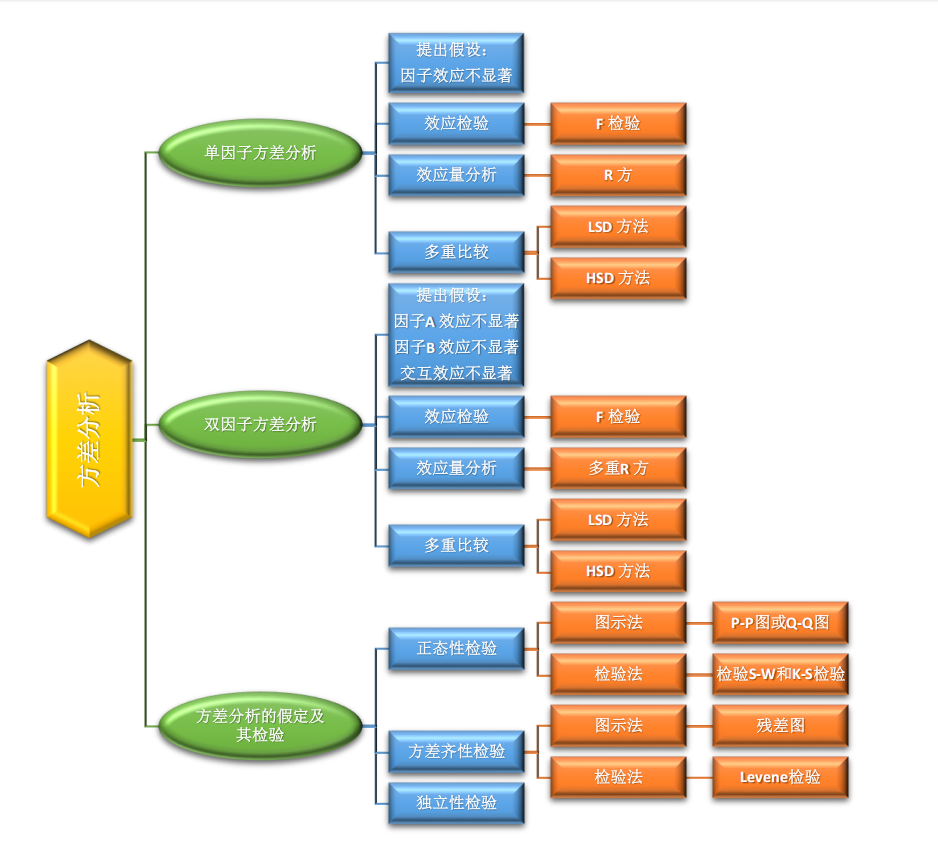
真題解讀

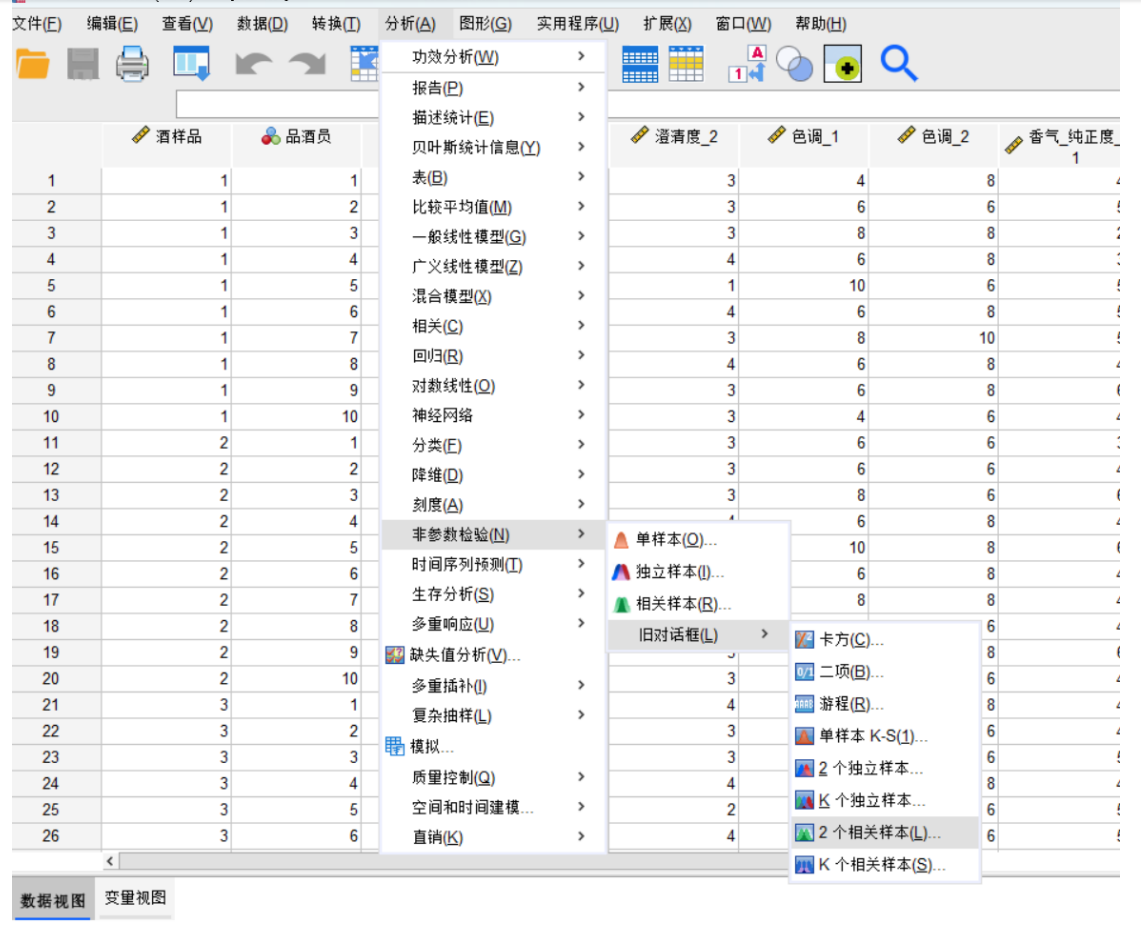
問題1的分析：兩組評酒員評價結果的顯著性差異及可信度比較

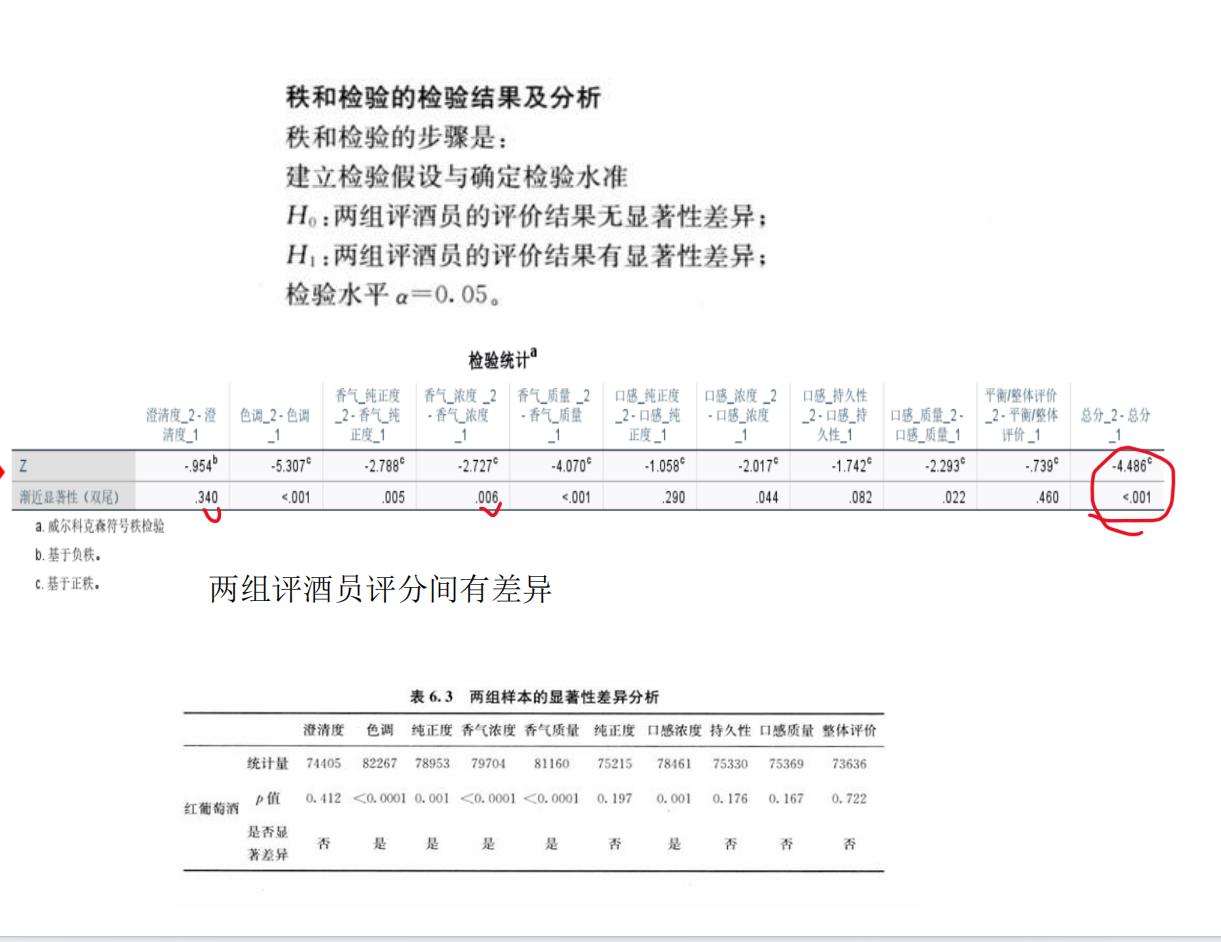
步驟1：提出假設

原假設（H?）：兩組評酒員的評價結果無顯著性差異（即兩組評分均值相等）。
備擇假設（H?）：兩組評酒員的評價結果存在顯著性差異（即兩組評分均值不相等）。

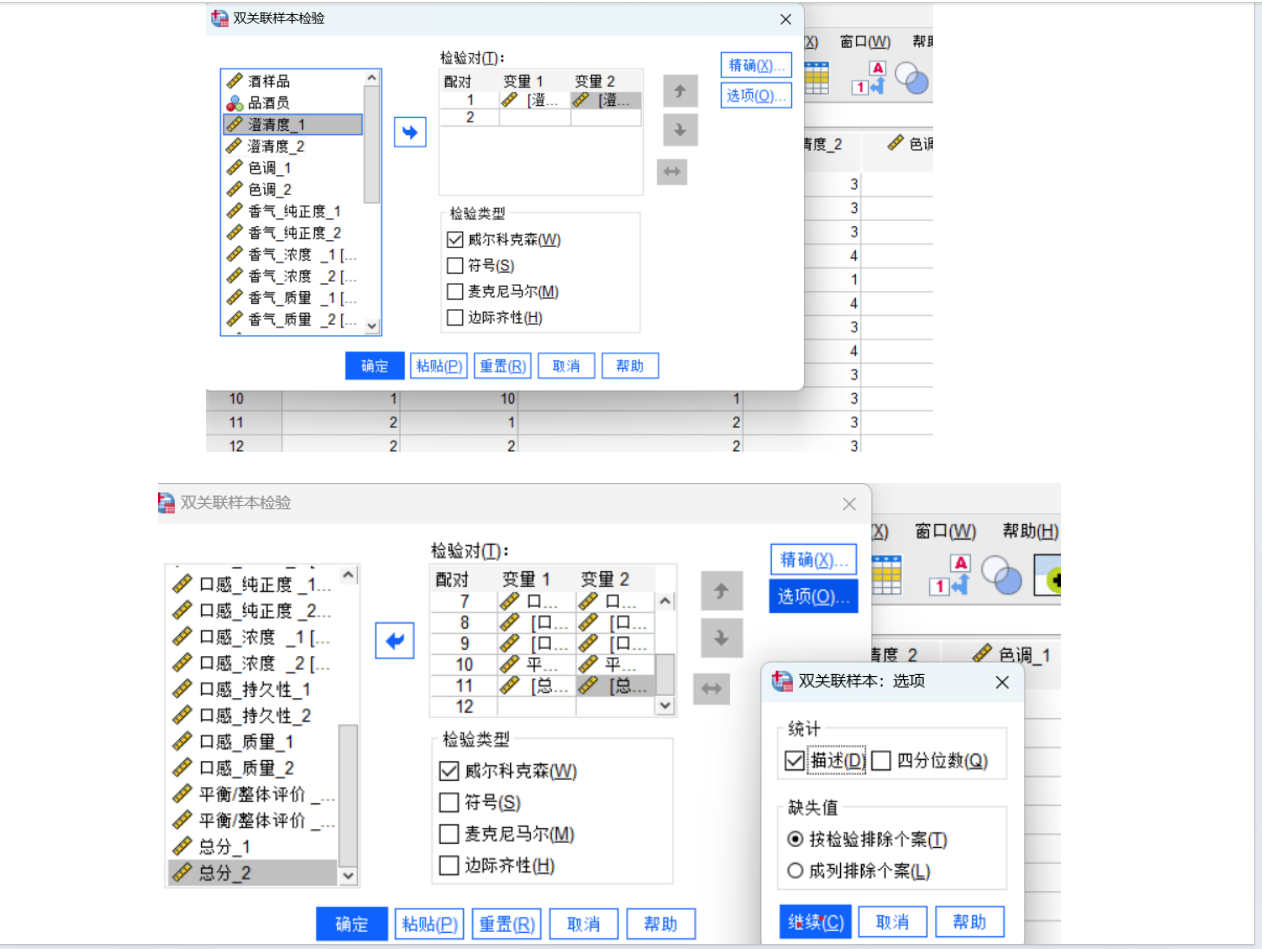
步驟2：選擇檢驗方法

由于附件1中包含兩組評酒員（每組多人）對多種葡萄酒的評分數據（連續數值），且需比較兩組獨立樣本的均值差異，我們選擇兩獨立樣本t檢驗（若數據符合正態性和方差齊性）或Mann-Whitney U檢驗（非參數檢驗，若數據不滿足正態性）。
理由：

每組評酒員對同一樣本（葡萄酒）的評分可視為一個組別的整體評價（可計算組內平均分或中位數）。
需要比較兩組評分的分布是否相同。

步驟3：確定顯著性水平

設定顯著性水平α = 0.05（即95%置信水平）。
若p值 < 0.05，則拒絕原假設，認為兩組存在顯著差異；否則接受原假設。

步驟4：計算檢驗統計量

假設附件1中數據已整理為如下形式（示例）：

組1（第一組評酒員）的評分樣本：

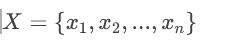
組2（第二組評酒員）的評分樣本：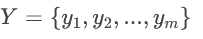

具體操作：

檢查數據正態性（如Shapiro-Wilk檢驗）和方差齊性（如Levene檢驗）。
- 若滿足正態性和方差齊性，使用兩獨立樣本t檢驗：
  統計量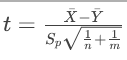，其中 Sp為合并標準差。

若不滿足，使用Mann-Whitney U檢驗（秩和檢驗）：
統計量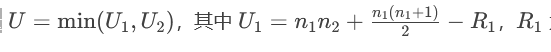為組1的秩和。

2.計算p值。

步驟5：決策規則

若p值 < α（0.05），拒絕H?，認為兩組評價存在顯著差異。
若p值 ≥ α，接受H?，認為無顯著差異。

步驟6：計算并得出結論

（以實際數據計算，此處為示例流程）
假設計算得到：

t檢驗統計量t = -2.34，p值 = 0.021（<0.05）
→ 拒絕H?，兩組評分存在顯著差異。

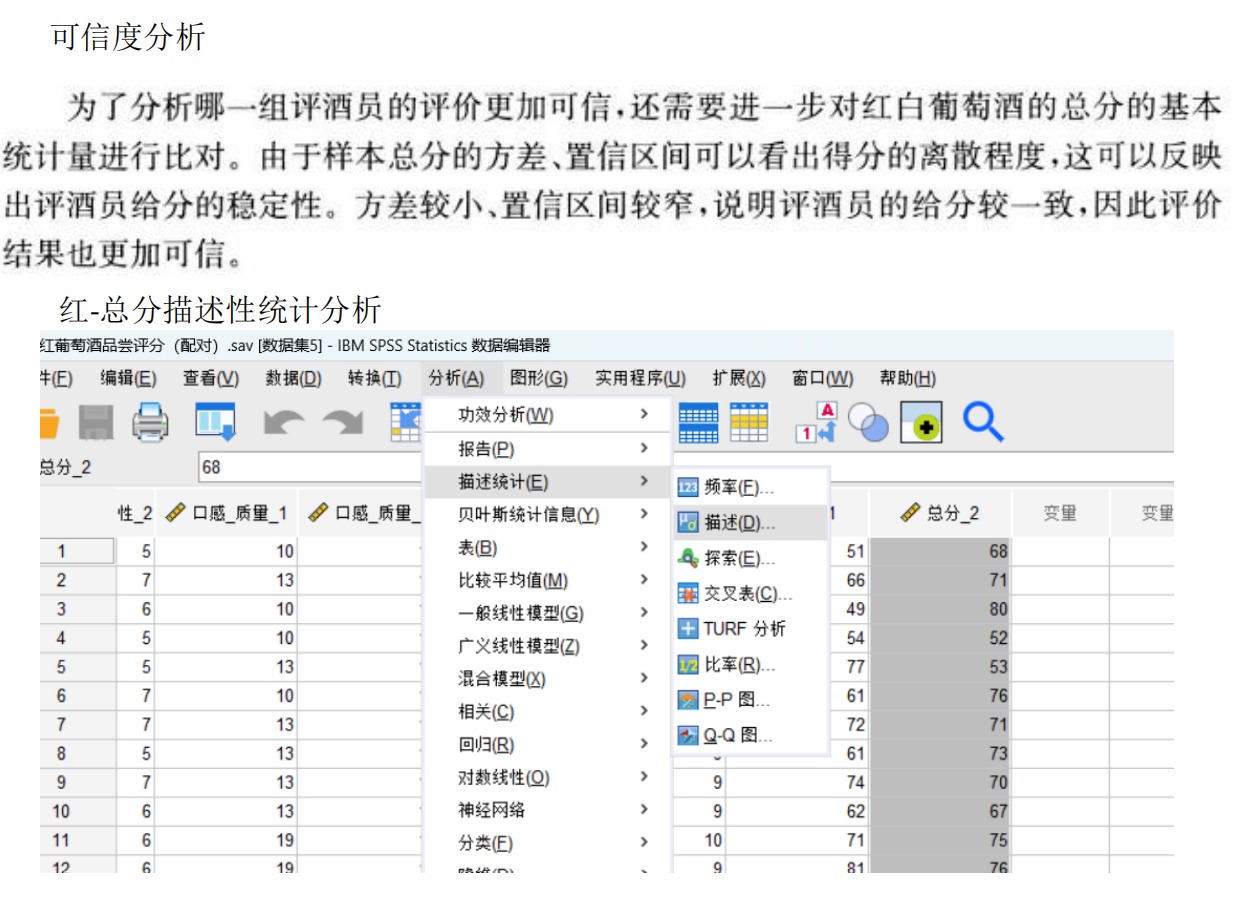
步驟7：結合可信度評價

哪一組更可信？
在存在顯著差異的基礎上，進一步評估可信度：

計算組內一致性（如組內評分標準差、變異系數CV或組內相關系數ICC）：
- 標準差越小、CV越小或ICC越高（接近1），說明組內評分一致性越好，可信度越高。
與客觀標準關聯（若存在外部基準，如葡萄酒真實質量，但本題無外部數據，故僅依賴內部一致性）。
常見結論：若一組評酒員組內一致性顯著高于另一組（如更低的標準差或更高的ICC），則該組更可信。

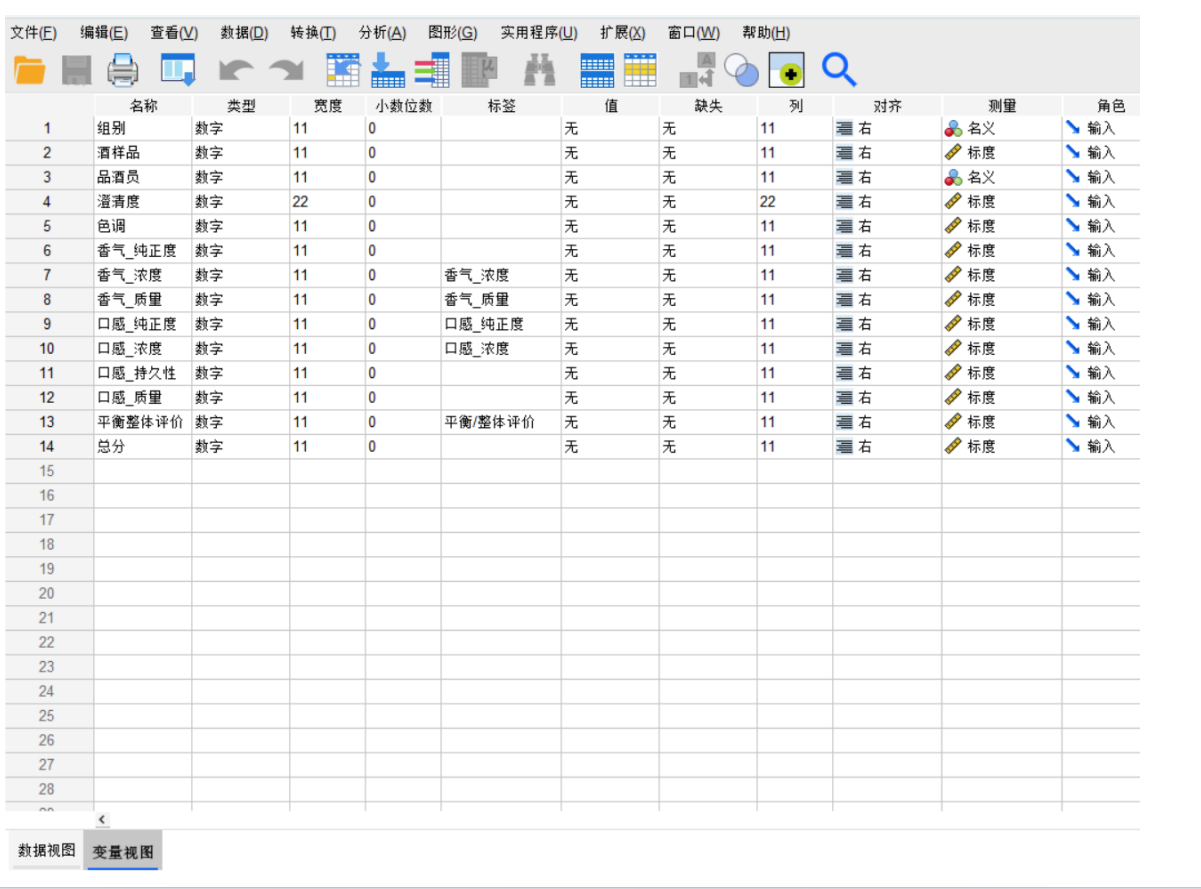
SPSS（Statistical Package for the Social Sciences，社會科學統計包）是一款非常強大且流行的統計分析軟件，現在官方名稱為 IBM SPSS Statistics。

一、核心概念：先理解兩個主要界面

SPSS主要有兩個核心窗口，幾乎所有操作都在這兩個窗口中進行：

數據視圖：
- 長得像Excel表格。這是您直接查看、錄入和修改原始數據的地方。
- 每一行代表一個案例（例如，一位受訪者、一只實驗小鼠、一家公司）。
- 每一列代表一個變量（例如，性別、年齡、收入、測試分數）。
變量視圖：
- 這是SPSS的靈魂所在，是定義“數據視圖”中每一列（變量）屬性的地方。很多新手出錯都是因為沒定義好變量。
- 在這里，您需要為每個變量設置關鍵屬性：
  - 名稱：變量的簡短標識（如 age, gender）。
  - 類型：數字、字符串（文本）、日期等。最常用的是“數值”。
  - 寬度和小數：數字的長度和小數點位數。
  - 標簽：對變量名稱的詳細解釋（如名稱是 q1，標簽可以寫“您對當前服務是否滿意？”）。強烈建議使用，能讓輸出結果更易讀。
  - 值：為數字代碼賦值（例如，定義 1 = 男， 2 = 女）。對于分類變量至關重要！
  - 測量尺度：
    - 標度：連續數據，如年齡、收入、分數（可進行加減乘除）。
    - 有序：等級數據，如滿意度（1.非常不滿意，2.不滿意，3.一般，4.滿意，5.非常滿意）。
    - 名義：分類數據，如性別、職業、省份（只是類別，無順序和大小之分）。

簡單比喻：數據視圖是答卷本身，填滿了答案；變量視圖是答題卡上的題目說明，規定了每道題是單選還是多選，選項1代表什么，2代表什么。

二、基本操作流程

使用SPSS進行分析通常遵循以下步驟：

第1步：定義變量
在 變量視圖 中，提前設置好所有需要的變量（列）及其屬性（特別是“標簽”和“值”）。

第2步：錄入數據
切換到 數據視圖，像在Excel中一樣，將收集到的數據逐行（每個個案）錄入進去。

第3步：數據清理和準備
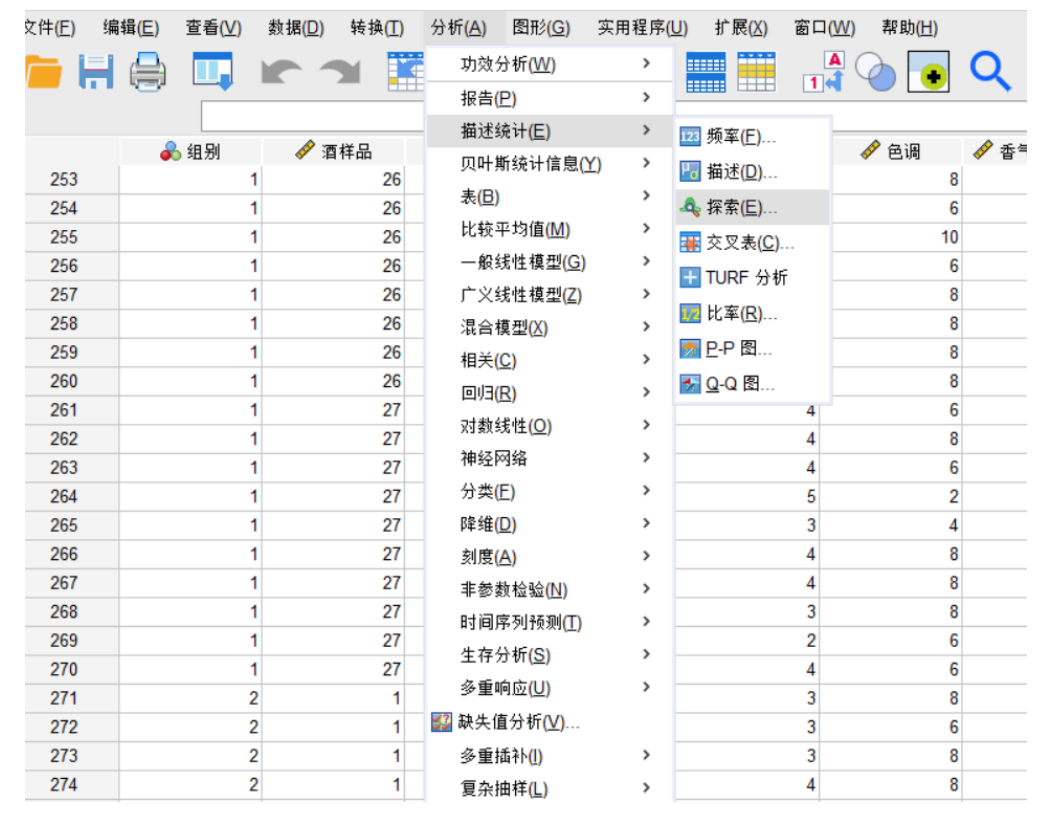
在進行分析前，通常需要檢查數據。

查找異常值：通過“分析” -> “描述統計” -> “頻率”或“描述”來查看數據的最大最小值是否合理。
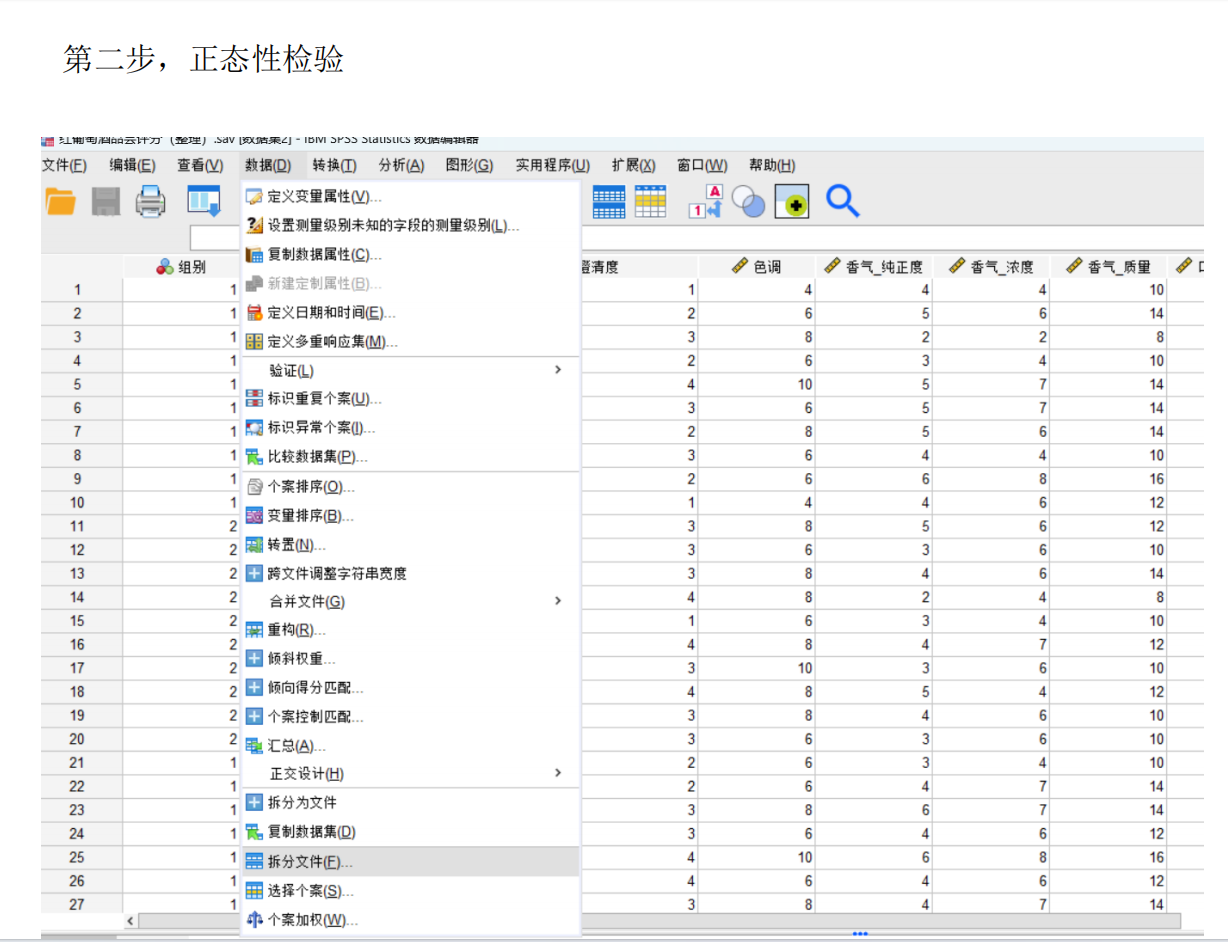
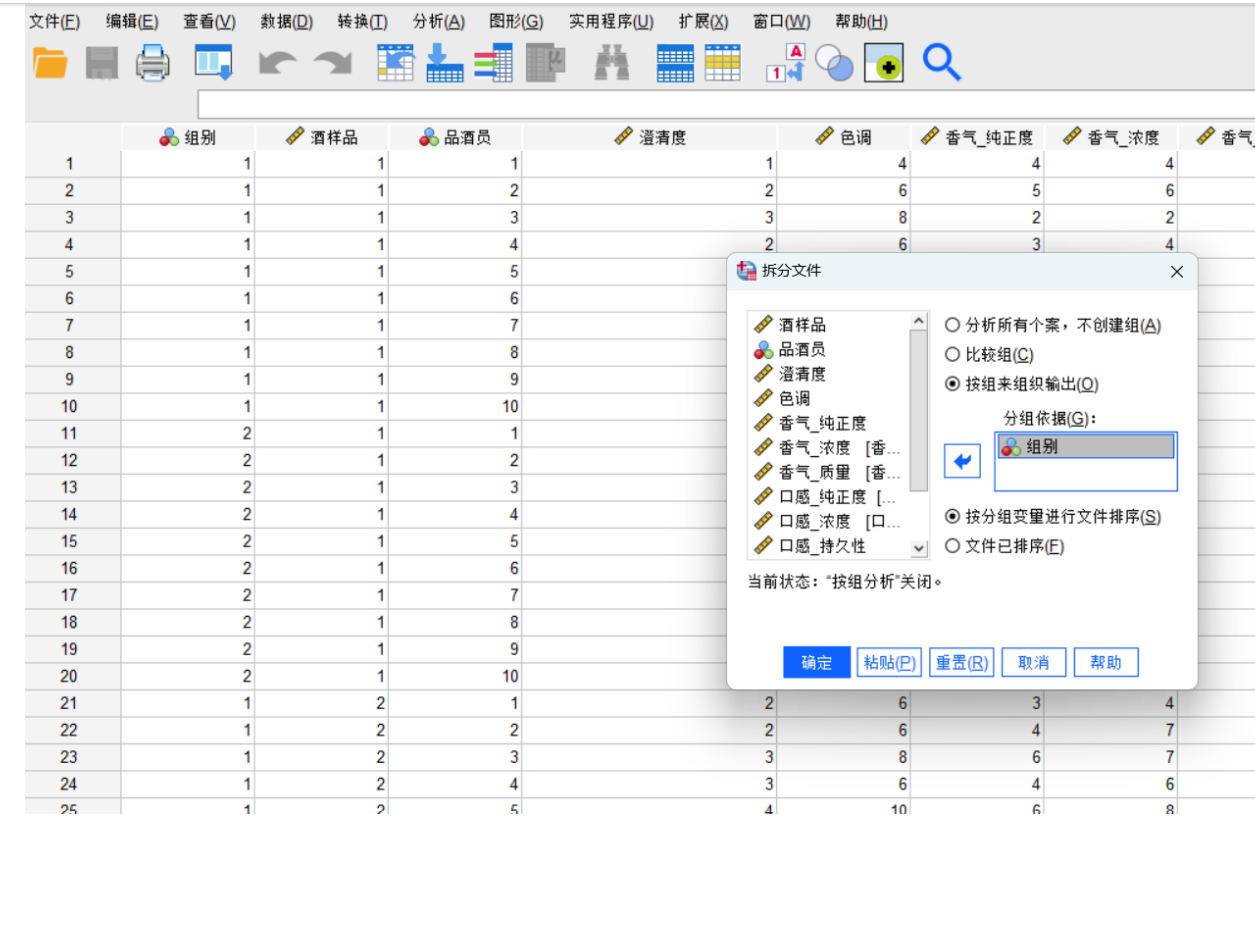
處理缺失值：檢查數據中是否有空白格，并決定如何處理（刪除、替換等）。
轉換變量：有時需要生成新變量，例如將總收入轉換為“人均收入”（轉換 -> 計算變量）。

第4步：選擇分析方法并執行
這是核心步驟。通過頂部的菜單欄 分析 來選擇你需要的方法。

想了解基本情況？ -> 描述統計
想比較兩組數據的平均值？ -> 比較均值 -> 獨立樣本T檢驗 或 配對樣本T檢驗
想分析兩個變量是否相關？ -> 相關 -> 雙變量
想用多個變量預測一個結果？ -> 回歸 -> 線性

第5步：解讀輸出結果
點擊分析后，會彈出一個新的 “查看器”窗口。所有的統計表格和圖表都會在這里顯示。您需要根據統計學知識來解讀這里的數字（如Sig./P值是否小于0.05，相關系數是多少等）。

三、常用功能快速入門

描述性統計
- 操作：分析 -> 描述統計 -> 頻率 或 描述
- 用途：快速了解數據的集中趨勢（平均值、中位數）和離散趨勢（標準差、最小值、最大值）。頻率 主要用于分類變量，能看到百分比。
T檢驗 - 比較兩組平均值
- 獨立樣本T檢驗（比如比較男性和女性的平均收入是否不同）：
  - 分析 -> 比較均值 -> 獨立樣本T檢驗
  - 將“收入”選入檢驗變量，將“性別”選入分組變量，然后點擊定義組，輸入男和女對應的數字代碼（如1和2）。
相關分析
- 操作：分析 -> 相關 -> 雙變量
- 用途：分析兩個或多個變量（如學習時間和考試成績）之間的相關程度和方向。主要看“皮爾遜相關系數”和“顯著性”。
回歸分析
- 操作：分析 -> 回歸 -> 線性
- 用途：研究一個因變量（結果）如何被多個自變量（預測因素）影響。比如“房價”如何被“面積”、“地段”、“樓層”影響。主要看R方、ANOVA表的Sig.值和系數表。
繪制圖表
- 操作：圖形 -> 舊對話框 -> 里面有各種圖表類型（條形圖、折線圖、散點圖等）。新版也提供了更現代的 圖表構建器，可以通過拖拽方式自定義圖表。

四、給新手的建議

不要害怕英文界面：SPSS有官方中文版，但很多教程和學術資源仍使用英文術語。熟悉 Variable View, Value Labels, Sig. (p-value) 等關鍵英文詞會對你更有幫助。
從數據入手：真正理解你每個變量的含義和測量尺度，這是正確選擇統計方法的基礎。
邊學邊練：找一份簡單的示范數據（網上很多），跟著教程一步一步操作，看結果是如何產生的。
理解輸出：軟件只會給你輸出一堆數字，關鍵在于你能否解讀出這些數字背后的統計學意義和現實意義。P值（Sig.）< 0.05 通常被認為是具有“統計學顯著性”的黃金標準。
善用幫助：SPSS內置的幫助文檔非常詳細，遇到任何功能不懂，直接按F1或點擊幫助菜單搜索。

總結一下：SPSS的操作邏輯是 “定義變量 -> 錄入數據 -> 選擇菜單進行分析 -> 解讀輸出結果”。

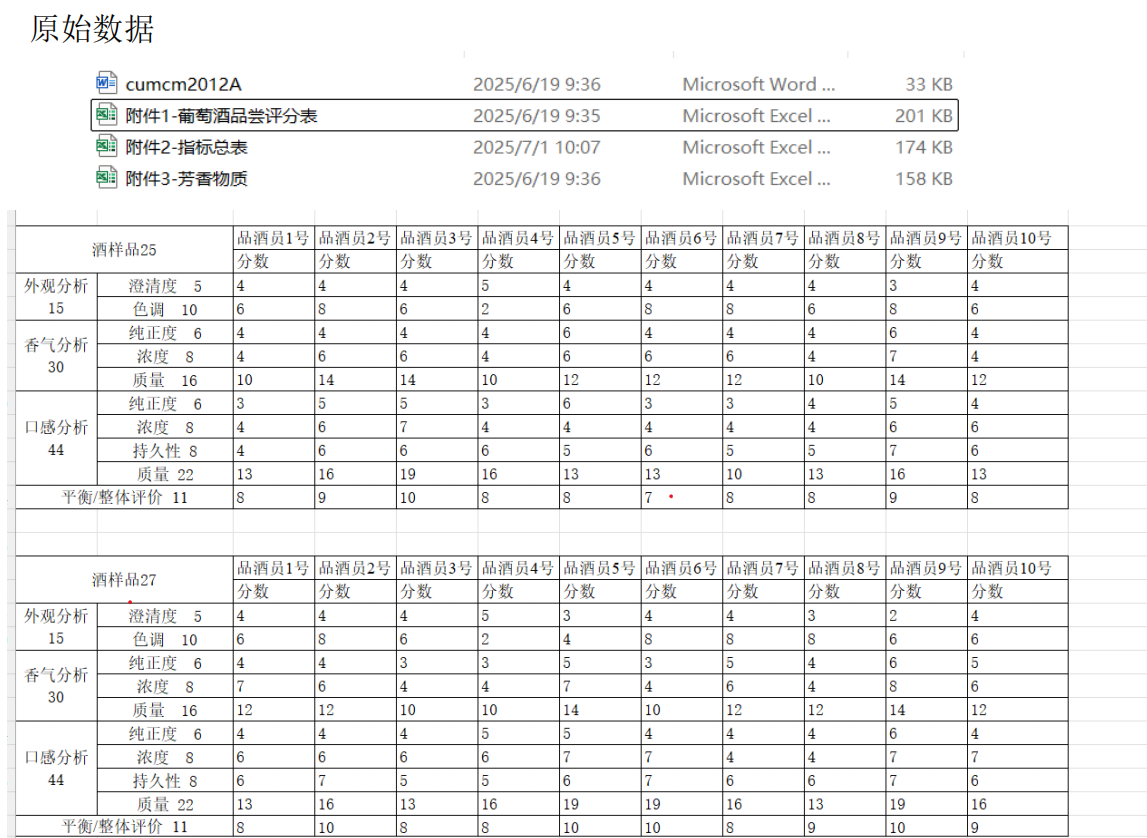
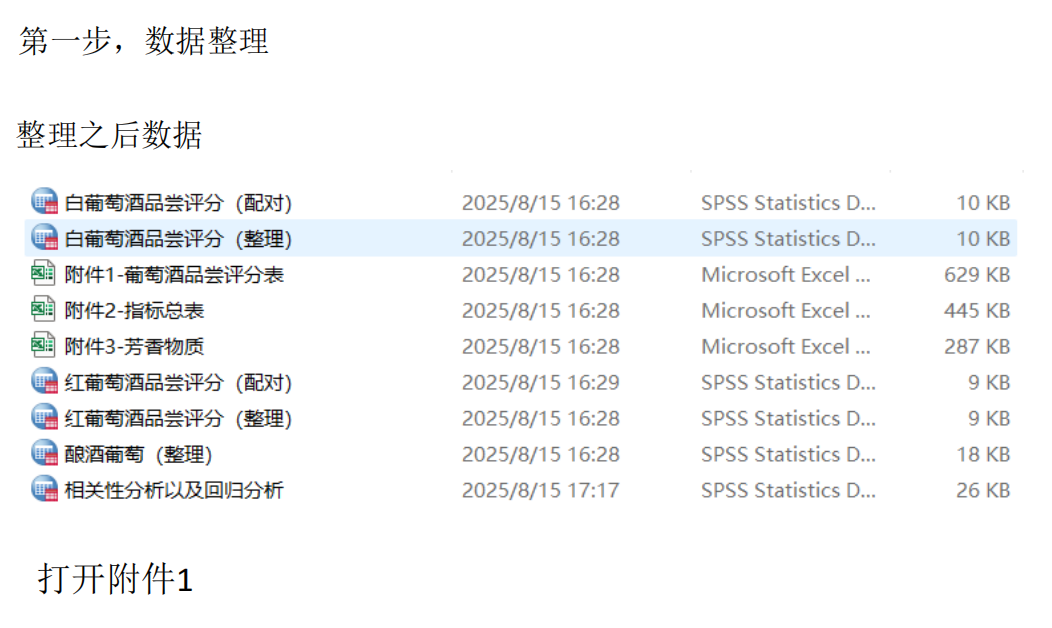
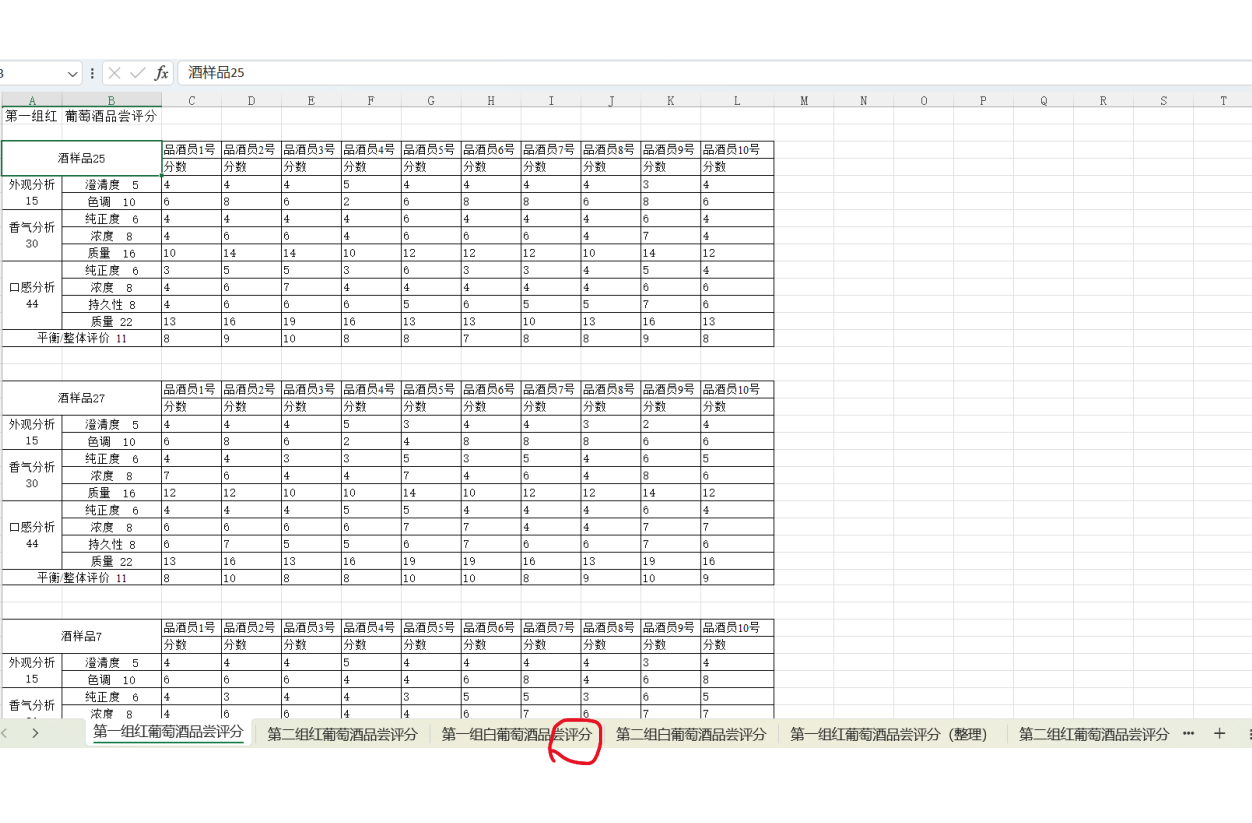
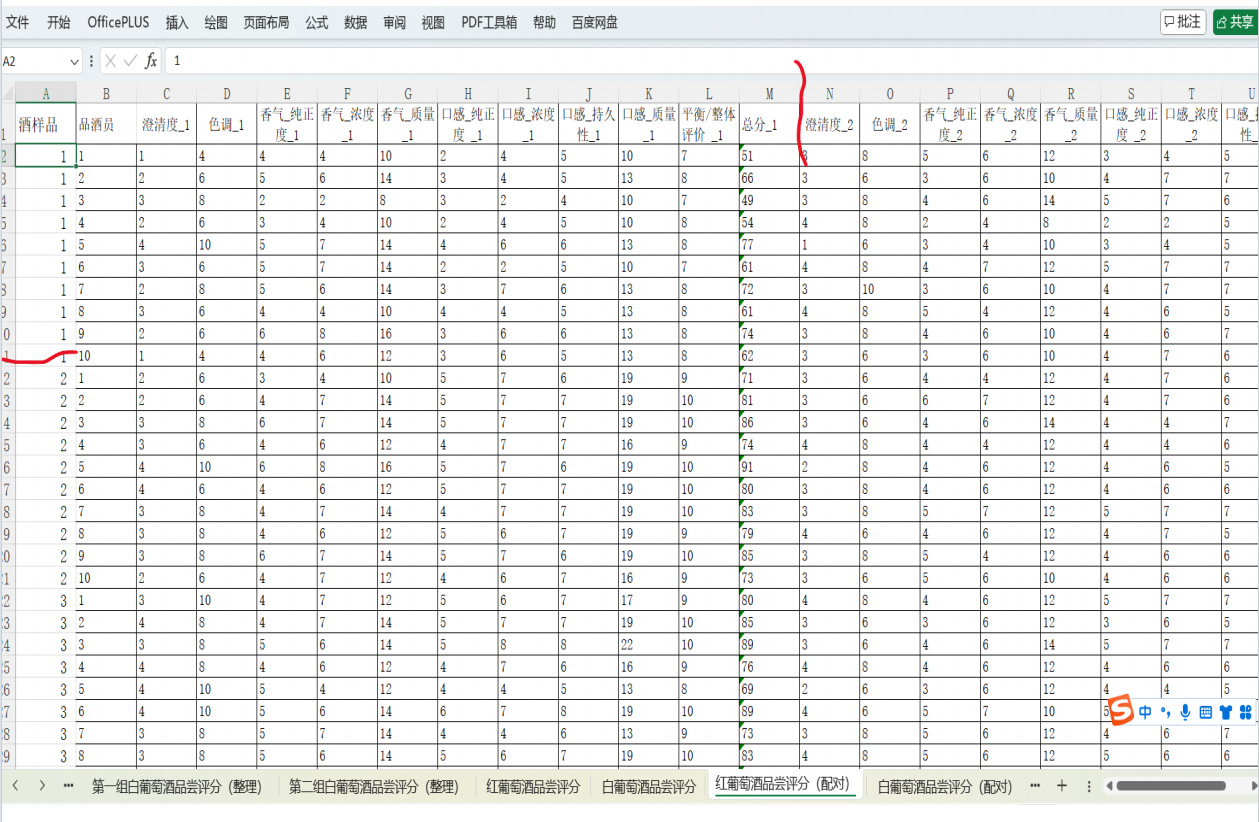
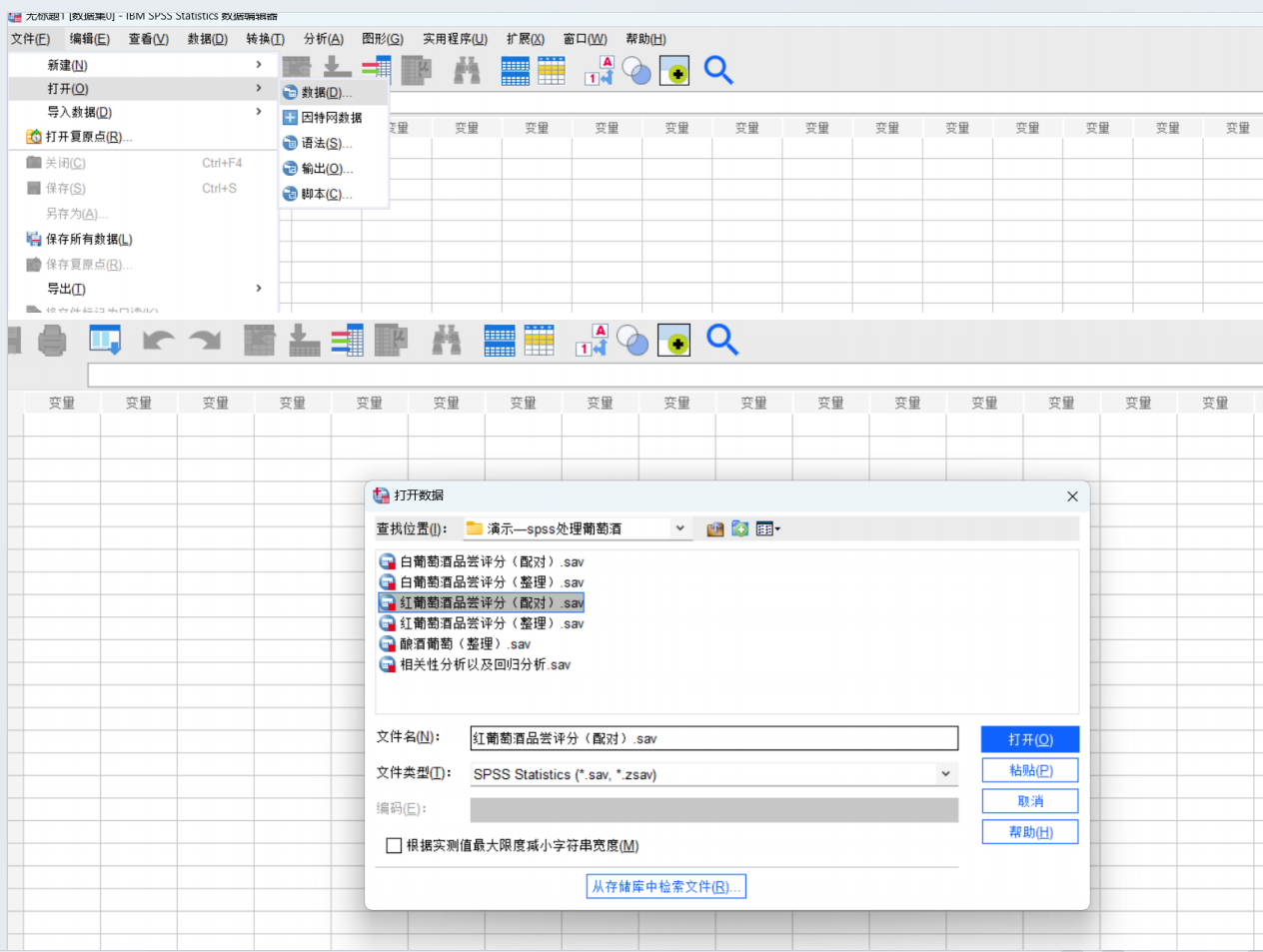
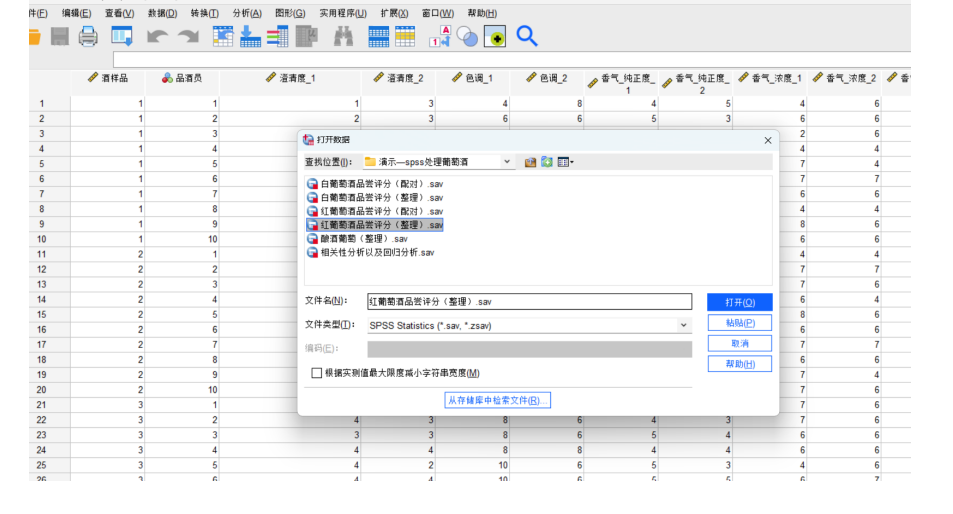
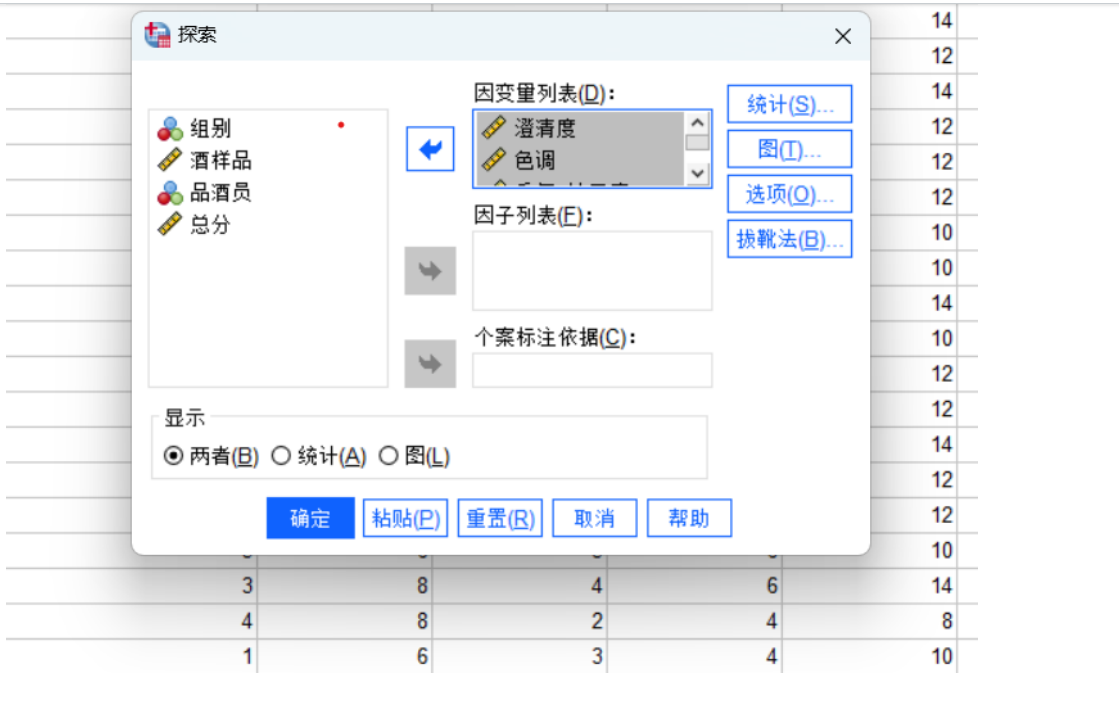
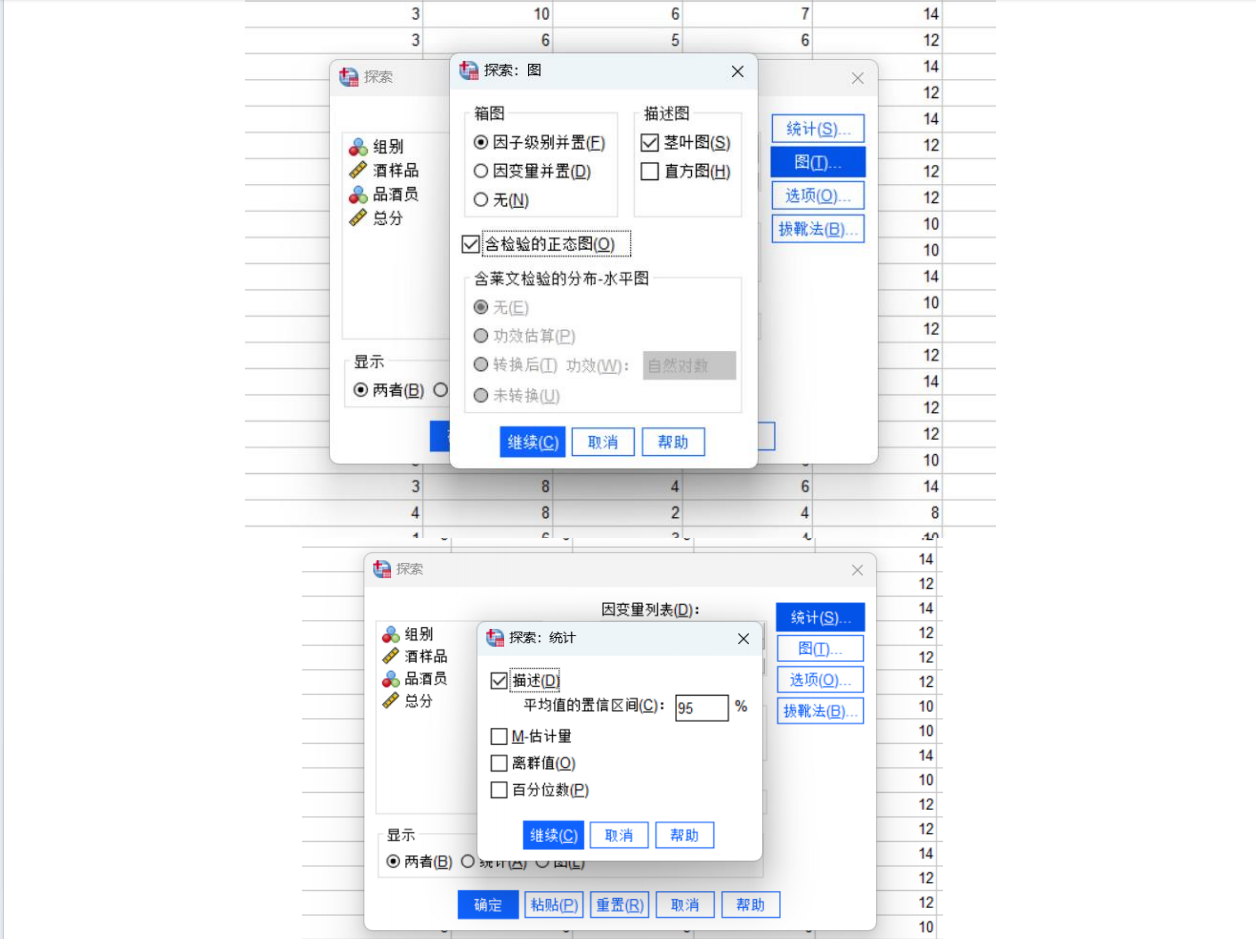
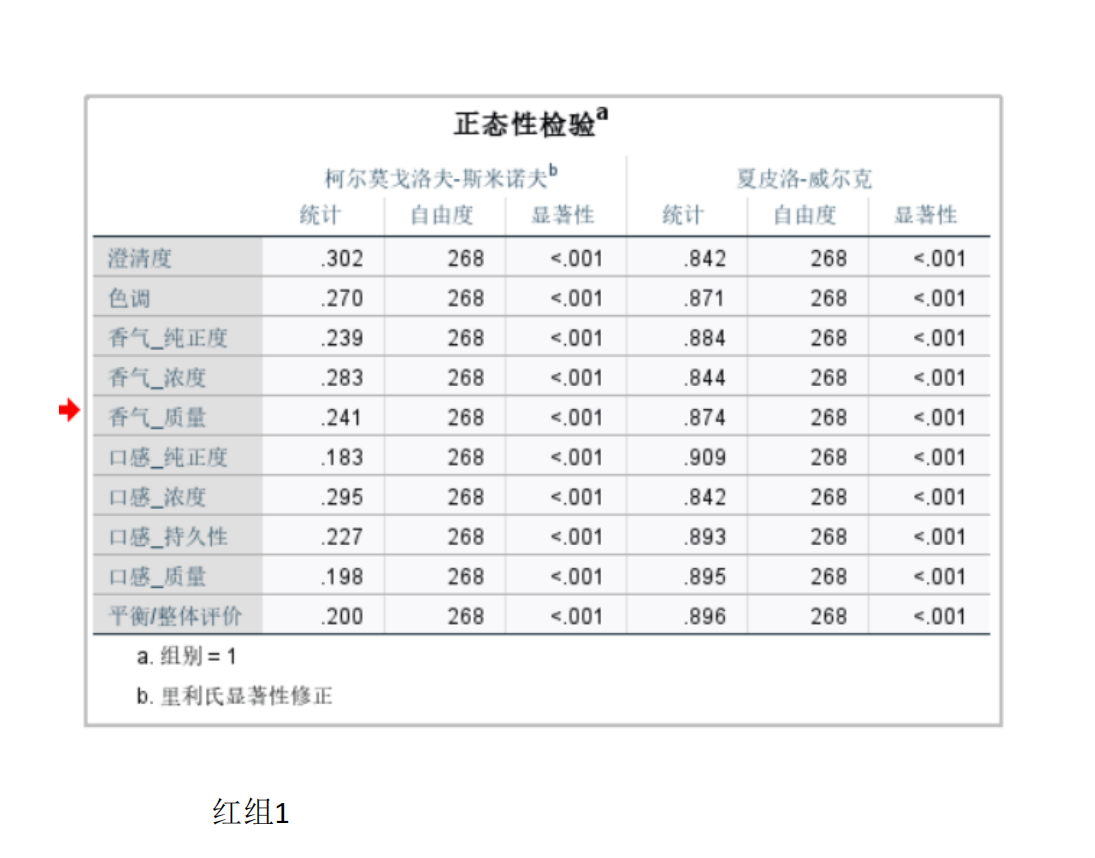
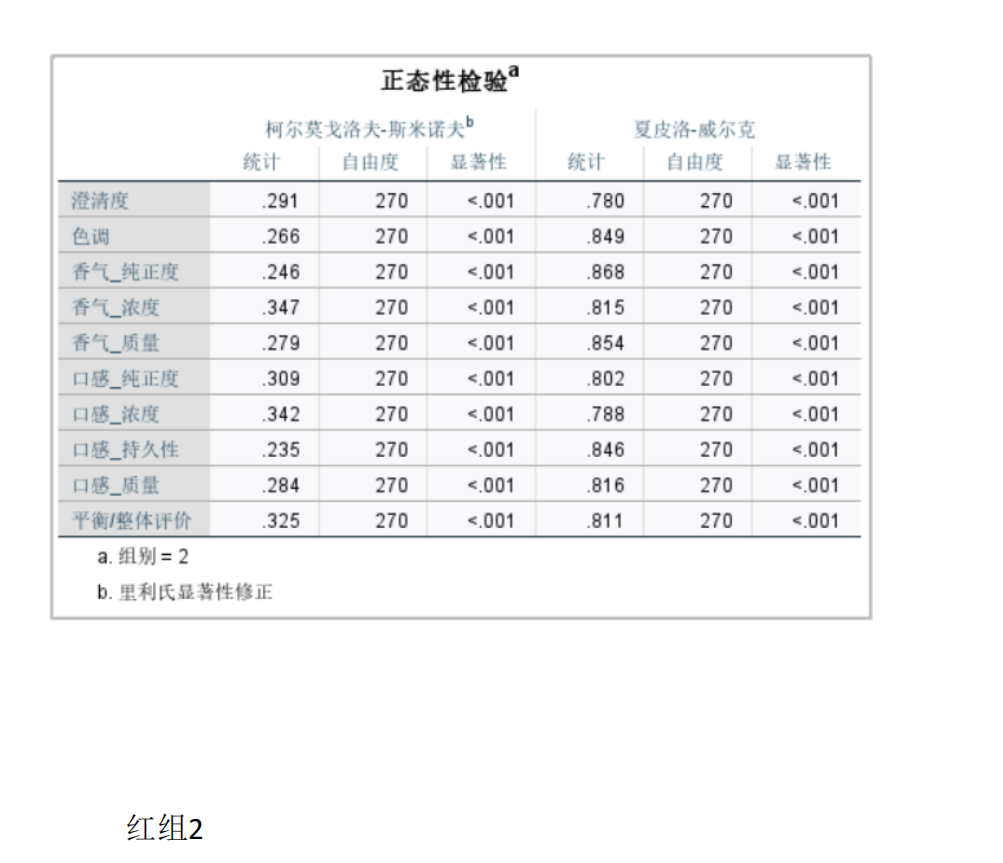
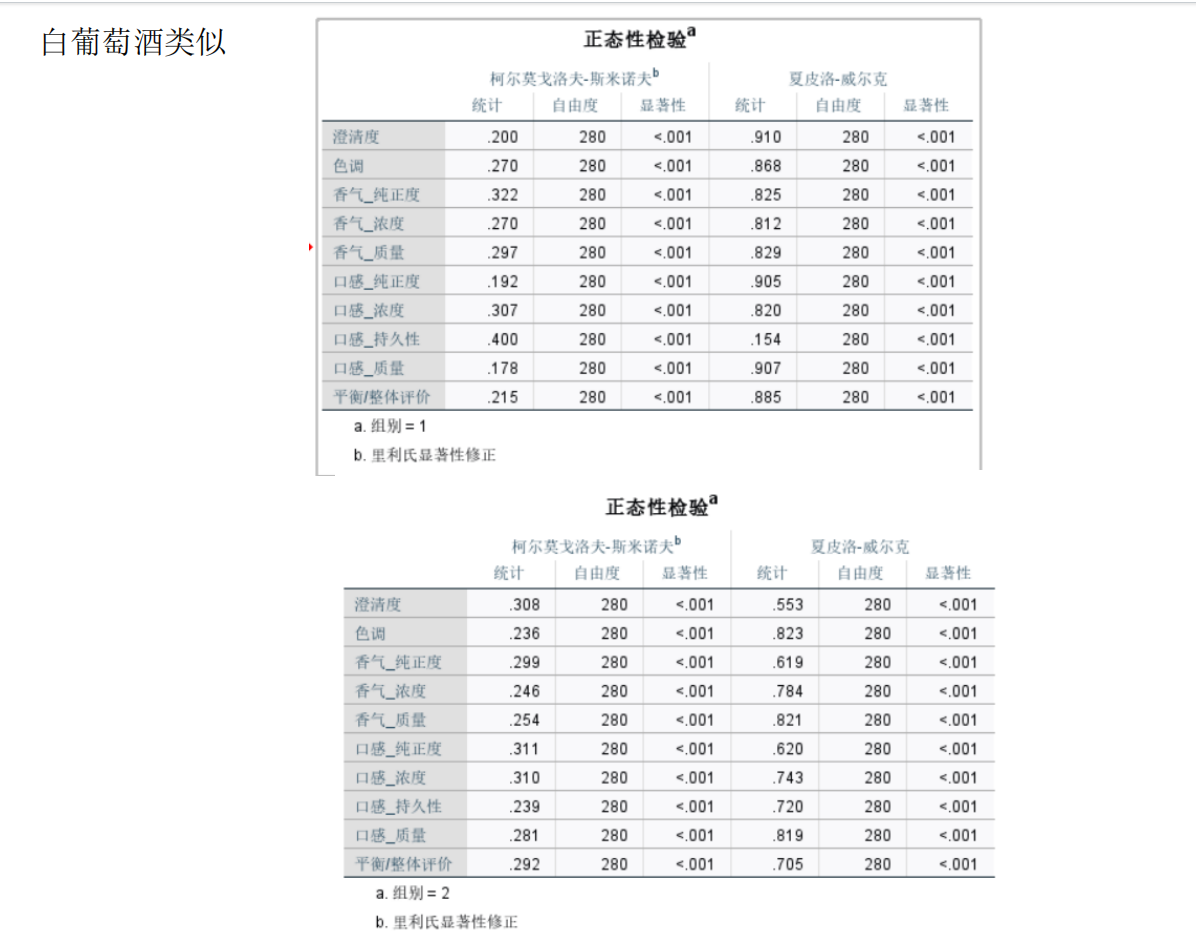
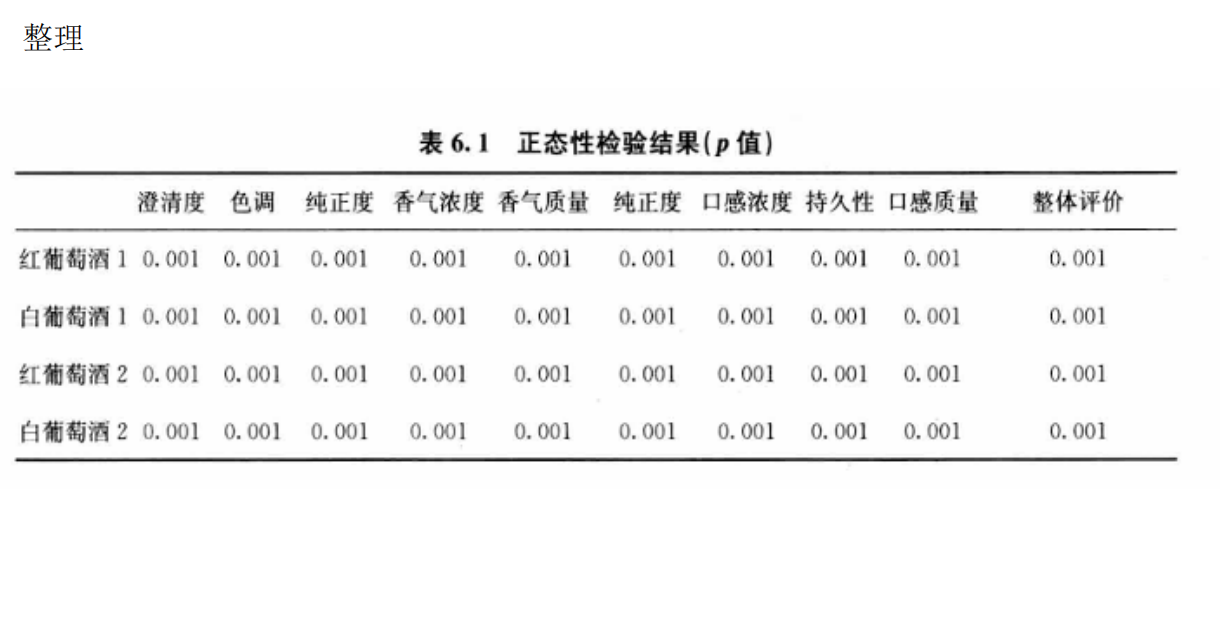
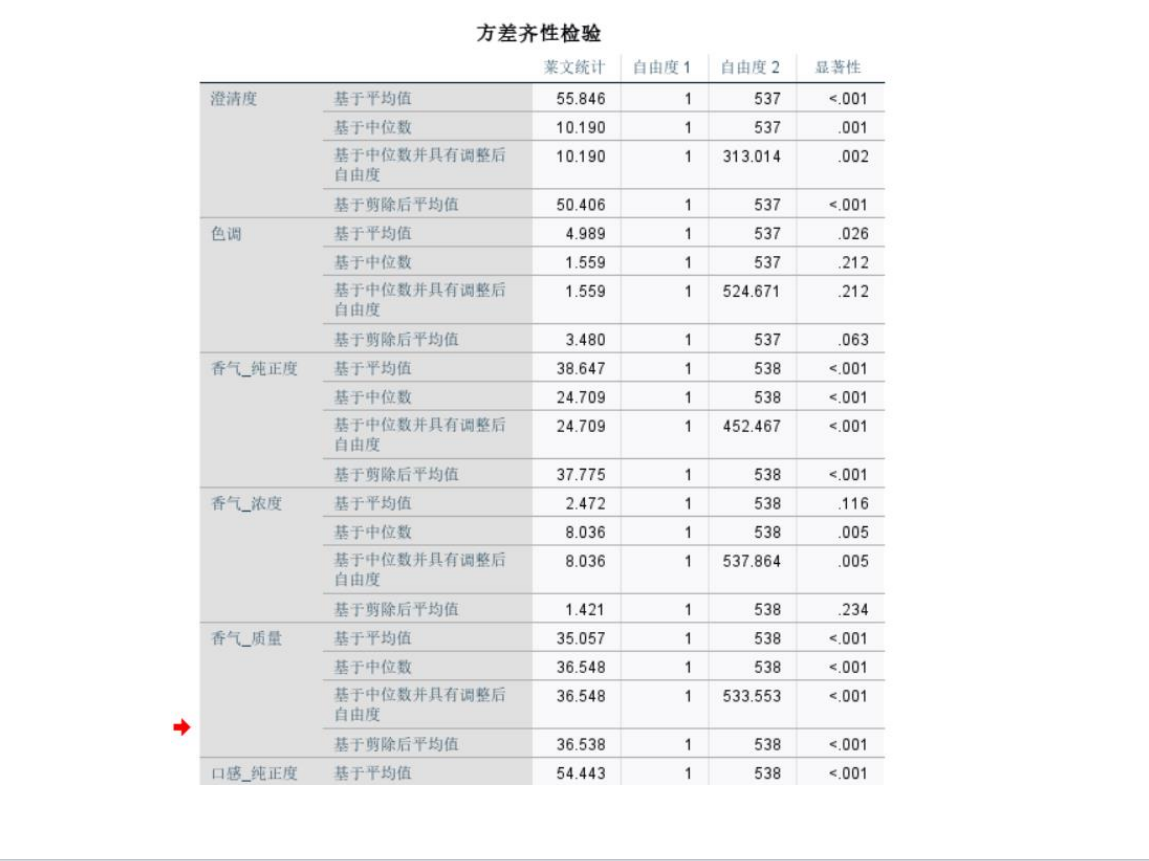
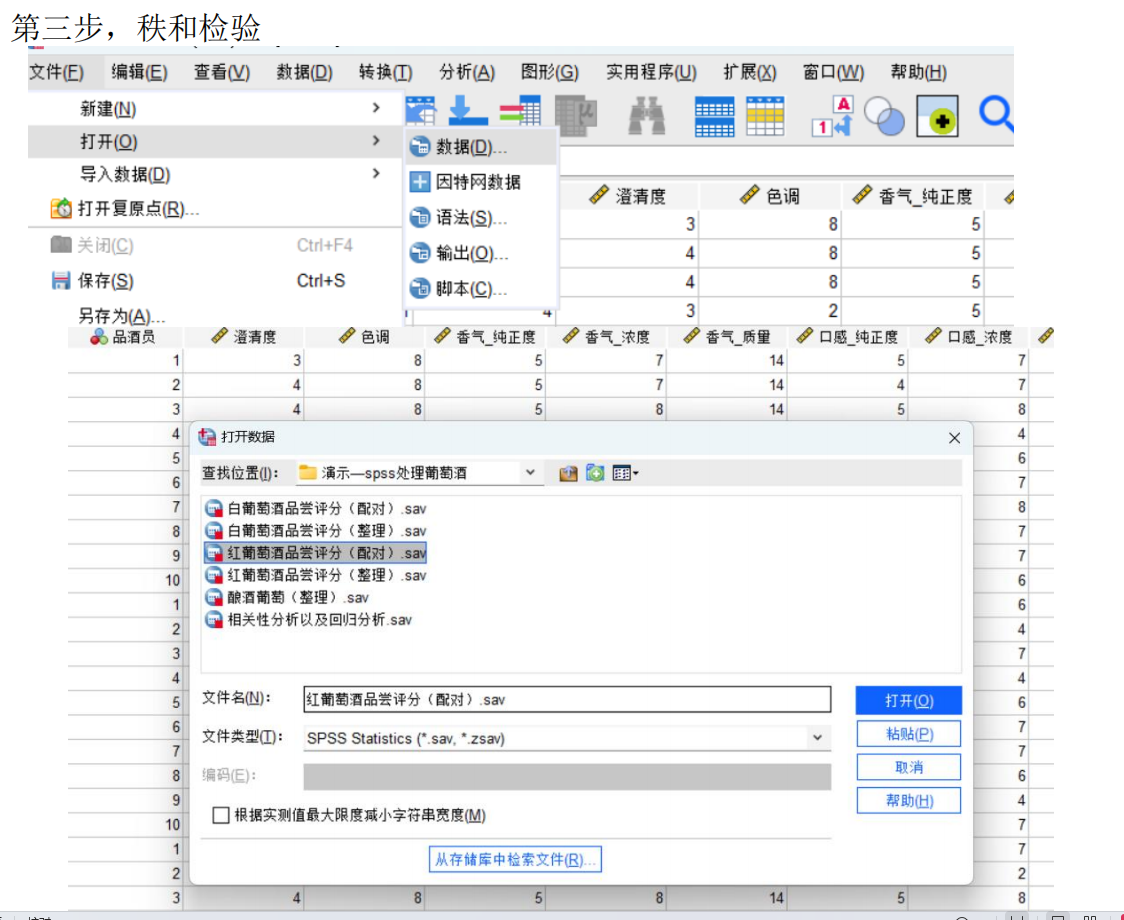
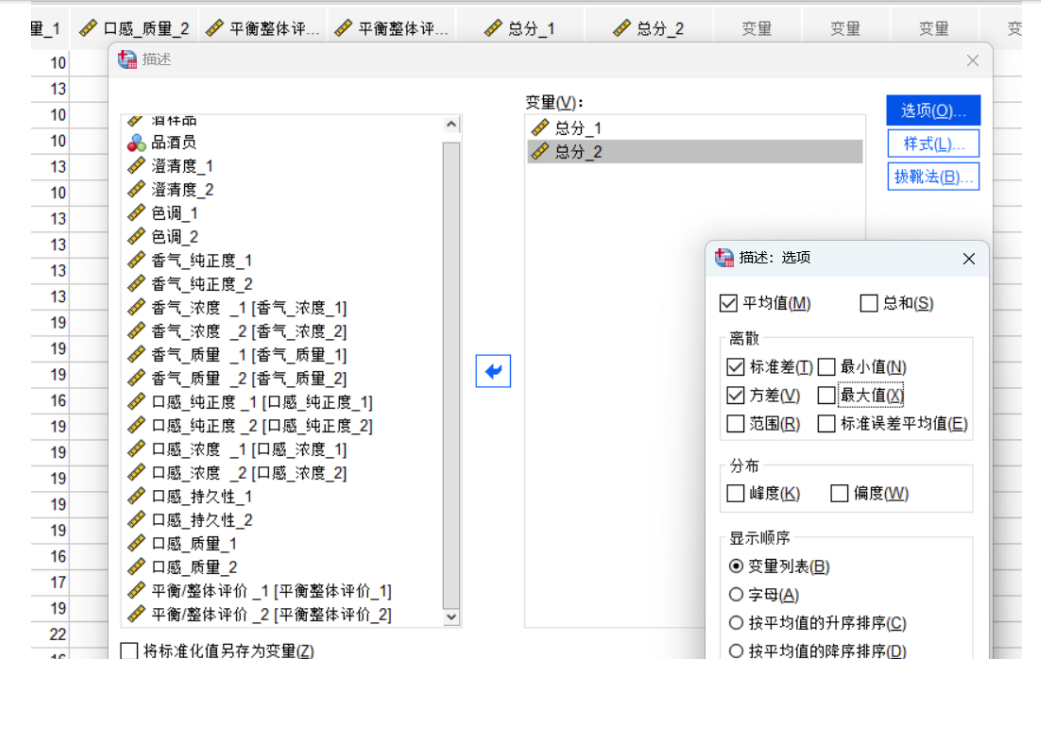
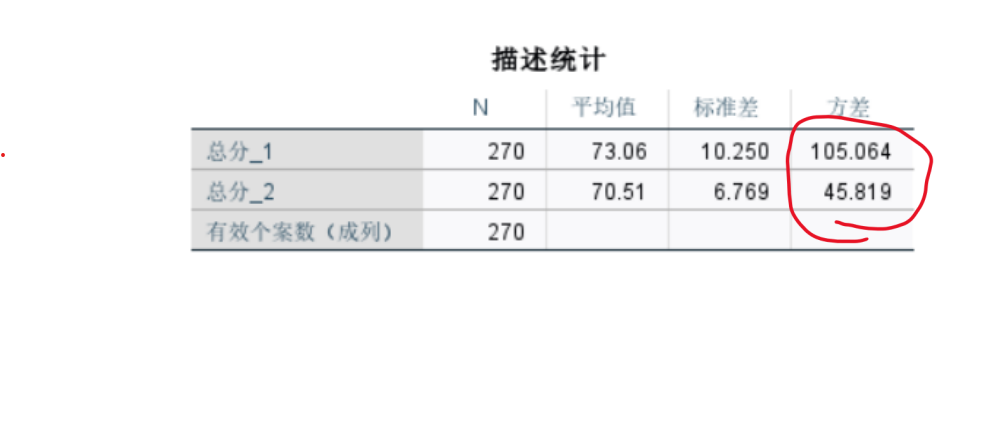
要在Python中解決葡萄酒評價問題，特別是進行假設檢驗和方差分析，可以使用pandas、scipy和statsmodels等庫。以下是一個完整的解決方案，涵蓋了如何使用Python分析不同評酒員對葡萄酒評分的差異，以及探究葡萄酒的理化指標或芳香物質對評分的影響。

一、問題重述與理解

問題背景：
分析多個葡萄酒樣品的品嘗評分數據，以及葡萄酒的各項理化指標和芳香物質含量數據，以確定：

不同評酒員對葡萄酒的評分是否存在顯著差異。
葡萄酒的某些理化指標或芳香物質是否對評分有顯著影響。

二、數據準備與預處理

數據導入：
- 使用pandas的read_excel函數從Excel文件中導入數據。
- 假設《附件1-葡萄酒品嘗評分表.xls》包含評酒員對各個葡萄酒樣品的評分數據，《附件2-指標總表.xls》包含葡萄酒的各項理化指標數據，《附件3-芳香物質.xls》包含葡萄酒的芳香物質含量數據。
數據預處理：
- 檢查數據完整性，處理缺失值和異常值。
- 對評分數據進行標準化處理（如果需要）。

三、假設檢驗與方差分析

1. 不同評酒員評分差異分析

假設：

H0（原假設）：不同評酒員對葡萄酒的評分沒有顯著差異。
H1（備擇假設）：不同評酒員對葡萄酒的評分有顯著差異。

方法：

使用單因素方差分析（One-Way ANOVA）來檢驗不同評酒員之間的評分是否存在顯著差異。

Python實現：

import pandas as pd
import scipy.stats as stats
import statsmodels.api as sm
from statsmodels.formula.api import ols# 導入評分數據
data = pd.read_excel('附件1-葡萄酒品嘗評分表.xls')# 假設數據表中有三列：'WineSample'（葡萄酒樣品），'Judge'（評酒員），'Score'（評分）
# 將數據重塑為適合ANOVA的格式
grouped_data = [data[data['Judge'] == judge]['Score'].values for judge in data['Judge'].unique()]# 進行單因素方差分析
f_val, p_val = stats.f_oneway(*grouped_data)# 顯示結果
print(f'ANOVA P-value: {p_val}')
if p_val < 0.05:print('拒絕原假設：不同評酒員的評分存在顯著差異。')
else:print('不拒絕原假設：沒有足夠證據表明不同評酒員的評分存在顯著差異。')# 如果需要多重比較，可以使用Tukey HSD檢驗（需要安裝statsmodels和scikit-posthocs）
# from scikit_posthocs import posthoc_tukey
# import numpy as np
# data_for_tukey = data[['Judge', 'Score']]
# judges_unique = data['Judge'].unique()
# data_for_tukey['Judge'] = pd.Categorical(data_for_tukey['Judge'], categories=judges_unique, ordered=True)
# data_for_tukey = data_for_tukey.sort_values('Judge')
# groups = data_for_tukey.groupby('Judge')['Score'].apply(list).values
# groups = [np.array(group) for group in groups]
# post_hoc_results = posthoc_tukey(data_for_tukey, val_col='Score', group_col='Judge')
# print(post_hoc_results)

2. 理化指標和芳香物質對評分的影響分析

單因子方差分析：

對每個理化指標或芳香物質，分別進行單因子方差分析，檢驗其對評分的影響是否顯著。

多元線性回歸：
2. 如果多個理化指標或芳香物質同時影響評分，可以使用多元線性回歸來探究它們對評分的聯合影響。

Python實現：

單因子方差分析示例（以某一理化指標為例）：

# 導入理化指標和評分數據
indicators = pd.read_excel('附件2-指標總表.xls')# 假設我們分析的理化指標為 'Indicator1'
# 合并評分數據和理化指標數據（這里需要假設數據合并的方式，例如按葡萄酒樣品ID）
# 假設 data 和 indicators 都有一個共同的列 'WineSample'
merged_data = pd.merge(data, indicators, on='WineSample')# 進行單因素方差分析（這里簡單示例，實際需要按Indicator1的分組）
# 假設我們將Indicator1分成兩組（高水平和低水平）進行示例
median_val = merged_data['Indicator1'].median()
high_level = merged_data[merged_data['Indicator1'] > median_val]['Score']
low_level = merged_data[merged_data['Indicator1'] <= median_val]['Score']f_val, p_val = stats.f_oneway(high_level, low_level)# 顯示結果
print(f'Indicator1 ANOVA P-value: {p_val}')
if p_val < 0.05:print('Indicator1 對評分有顯著影響。')
else:print('Indicator1 對評分沒有顯著影響。')

多元線性回歸示例：

# 假設我們分析多個理化指標對評分的影響
X = merged_data[['Indicator1', 'Indicator2', 'Indicator3']]  # 示例指標
y = merged_data['Score']# 添加常數項
X = sm.add_constant(X)# 擬合多元線性回歸模型
model = sm.OLS(y, X).fit()# 顯示回歸結果
print(model.summary())# 檢查哪些指標顯著
significant_indicators = model.pvalues[1:] < 0.05  # 排除截距項
print('顯著的理化指標：')
print(X.columns[1:][significant_indicators])

四、結果解釋與報告

對于第一問：

如果ANOVA結果顯示P值小于0.05，則拒絕原假設，認為不同評酒員的評分存在顯著差異。
通過多重比較（如Tukey HSD）進一步分析哪些評酒員之間的評分存在顯著差異。

對于第二問：

通過單因子ANOVA和多元線性回歸，可以確定哪些理化指標或芳香物質對評分有顯著影響。
根據回歸模型的系數和P值，可以判斷各指標對評分的貢獻程度和顯著性。

五、具體Python操作示例（以第一問為例）

數據準備：
- 確保數據已正確導入Python，且數據已按評酒員和葡萄酒樣品整理。
單因子ANOVA：
- 使用scipy.stats.f_oneway函數進行單因子方差分析。
- 記錄每個因素的F值和P值，判斷其是否對評分有顯著影響。
多元線性回歸：
- 使用statsmodels.api.OLS進行多元線性回歸分析。
- 顯示回歸模型的系數和P值，確定哪些理化指標或芳香物質對評分有顯著影響。

六、結論與報告

根據分析結果，寫報告或論文，包括：

摘要：簡要概述研究目的、方法和主要發現。
引言：介紹葡萄酒評價的背景和重要性。
方法：描述使用的統計方法和Python實現過程。
結果：展示ANOVA和回歸分析的結果，包括顯著差異和影響因素。
討論：解釋結果的實際意義，提出可能的改進或未來研究方向。

MATLAB 實現：

% 導入評分數據
data = readtable('附件1-葡萄酒品嘗評分表.xls');% 假設數據表中有三列：'WineSample'（葡萄酒樣品），'Judge'（評酒員），'Score'（評分）
% 將數據重塑為適合 ANOVA 的格式
judges = unique(data.Judge);
scores = {};
for i = 1:length(judges)scores{i} = data.Score(data.Judge == judges(i));
end% 進行單因素方差分析
[p, tbl, stats] = anova1(scores, judges, 'off');% 顯示結果
fprintf('ANOVA P-value: %f\n', p);
if p < 0.05fprintf('拒絕原假設：不同評酒員的評分存在顯著差異。\n');
elsefprintf('不拒絕原假設：沒有足夠證據表明不同評酒員的評分存在顯著差異。\n');
end

MATLAB 實現：

單因子方差分析示例（以某一理化指標為例）：

% 導入理化指標和評分數據
indicators = readtable('附件2-指標總表.xls');
scores = data.Score; % 假設已經從評分表中獲取了評分數據% 假設我們分析的理化指標為 'Indicator1'
indicatorData = indicators.Indicator1;% 進行單因素方差分析
[p, tbl, stats] = anova1([scores(indicatorData == lowLevel), scores(indicatorData == highLevel)], ...{'Low Level', 'High Level'}, 'off');% 顯示結果
fprintf('Indicator1 ANOVA P-value: %f\n', p);
if p < 0.05fprintf('Indicator1 對評分有顯著影響。\n');
elsefprintf('Indicator1 對評分沒有顯著影響。\n');
end

多元線性回歸示例：

% 假設我們分析多個理化指標對評分的影響
X = [indicators.Indicator1, indicators.Indicator2, indicators.Indicator3]; % 示例指標
y = scores;% 擬合多元線性回歸模型
mdl = fitlm(X, y);% 顯示回歸結果
disp(mdl);% 檢查哪些指標顯著
coefficients = mdl.Coefficients;
significantIndicators = coefficients.pValue(2:end) < 0.05; % 排除截距項
fprintf('顯著的理化指標：\n');
disp(indicators.Properties.VariableNames(2:end)(significantIndicators)); % 假設前兩列是指標名稱，根據實際情況調整