今天復習一下翻轉二叉樹

226. 翻轉二叉樹

給你一棵二叉樹的根節點?root?，翻轉這棵二叉樹，并返回其根節點。

示例 1：

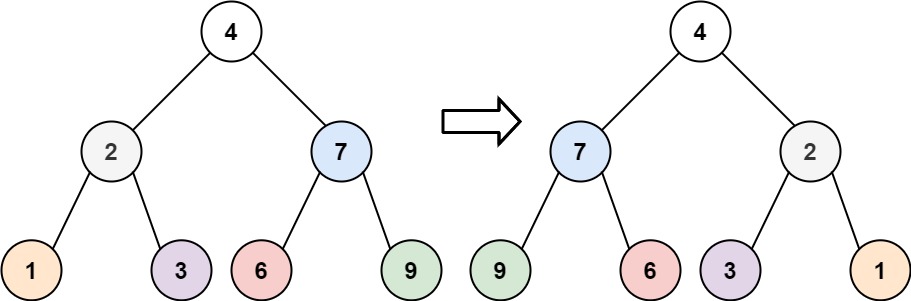
輸入：root = [4,2,7,1,3,6,9]
輸出：[4,7,2,9,6,3,1]

示例 2：

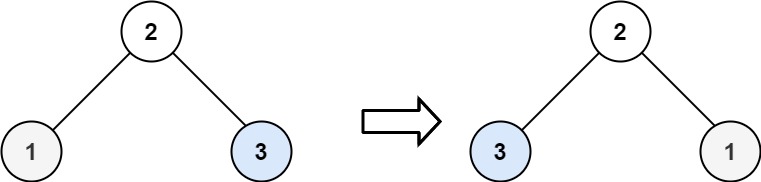
輸入：root = [2,1,3]
輸出：[2,3,1]

示例 3：

輸入：root = []
輸出：[]

提示：

• 樹中節點數目范圍在?[0, 100]?內
• -100 <= Node.val <= 100

1 我的想法以及分析

翻轉以后的二叉樹對于每一個子節點來說就是左右互換了。

但是我不知道具體要怎么實現這個，而且返回的root是有順序的，不知道怎么弄啊。

借鑒了一下題解，要用遞歸，那么。。算了一點看不懂，找一下以前寫的博客。

好難啊不知道這個遞歸什么鬼，也沒有個while for循環的，結束條件在哪里？也沒把判斷null放里頭啊。

我是豬。

2 解析

別慌！遞歸看起來 “沒有循環”，其實是把循環的邏輯交給了函數自身調用，咱們一步步拆解，保證能懂。

一、核心思路：為什么是 “左右互換”？

翻轉二叉樹的本質，是對每一個節點，交換它的左子樹和右子樹。

• 比如示例 1 中的根節點4，要交換它的左子樹（以2為根）和右子樹（以7為根）；
• 接著處理2這個節點，交換它的左子樹（1）和右子樹（3）；
• 再處理7這個節點，交換它的左子樹（6）和右子樹（9）；
• 直到遇到 “空節點”（沒有子樹可交換），就停止。

二、遞歸怎么寫？3 步理清邏輯

遞歸的核心是 “明確函數做什么、終止條件是什么、子問題怎么拆”，咱們對應到這道題：

1. 明確函數功能

定義函數invertTree(root)：

• 輸入：一個節點root（可能是根，也可能是子樹的根）；
• 輸出：翻轉該節點所在子樹后，新的根節點（其實就是原root，因為只是交換子樹，根不變）。

2. 終止條件（“什么時候停”）

當root是null時（比如葉子節點的左 / 右子樹，或者空樹），沒有子樹可交換，直接返回null即可。
這就是遞歸的 “出口”，避免無限調用。

3. 子問題拆解（“當前節點要做什么”）

對一個非空節點root，只需要 3 步：

1. 暫存左子樹：因為交換后會覆蓋左子樹，先把root.left存起來（比如叫leftTemp）；
2. 交換左右子樹：
   • 把root的左子樹，改成 “翻轉后的右子樹”（即調用invertTree(root.right)）；
   • 把root的右子樹，改成 “翻轉后的左子樹”（即調用invertTree(leftTemp)）；
3. 返回當前節點root（它的子樹已經翻轉完成）。

三、代碼實現（Java 示例）

java

運行

// 二叉樹節點定義
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {public TreeNode invertTree(TreeNode root) {// 終止條件：遇到空節點，直接返回nullif (root == null) {return null;}// 1. 暫存左子樹（避免交換時被覆蓋）TreeNode leftTemp = root.left;// 2. 交換：左子樹 = 翻轉后的右子樹，右子樹 = 翻轉后的左子樹root.left = invertTree(root.right);root.right = invertTree(leftTemp);// 3. 返回當前節點（子樹已翻轉）return root;}
}

四、用示例 1 驗證流程（幫你 “看見” 遞歸）

輸入：root = [4,2,7,1,3,6,9]（結構如下）

plaintext

    4/ \2   7/ \ / \
1  3 6  9

遞歸執行步驟（簡化）：

1. 處理4：暫存左子樹2，調用invertTree(7)（先翻轉右子樹）、invertTree(2)（再翻轉左子樹）；
2. 處理7：暫存左子樹6，調用invertTree(9)（返回9）、invertTree(6)（返回6），交換后7的左 = 9、右 = 6；
3. 處理2：暫存左子樹1，調用invertTree(3)（返回3）、invertTree(1)（返回1），交換后2的左 = 3、右 = 1；
4. 回到4：交換后4的左 = 7（已翻轉）、右 = 2（已翻轉），最終返回4。

最終結果就是[4,7,2,9,6,3,1]，和示例一致。

五、關鍵誤區糾正！！！！！！！！！！！

• 不是 “沒有循環”：遞歸的 “循環” 是通過函數調用實現的，每個節點都會被處理一次，終止條件if (root == null)就是 “循環停止” 的信號；
• 不用糾結 “返回順序”：遞歸會自動處理所有子節點，我們只需要關注 “當前節點要交換左右子樹”，剩下的交給子調用即可。

多拿幾個簡單例子（比如示例 2）走一遍流程，很快就能理解遞歸的 “自下而上” 處理邏輯啦！

3 自己重新理一遍

題目已給代碼

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode invertTree(TreeNode root) {}
}

if (root == null){

return null;

}

TreeNode left = invertTree(root.left);

//【我感覺有點像套娃?】

插播一條。

“套娃” 這個比喻特別精準！遞歸的核心邏輯其實就是 “套娃”，咱們可以順著這個比喻再拆解一層，幫你徹底打通思路：

一、遞歸 = “拆解套娃” + “組裝套娃”

翻轉二叉樹的遞歸過程，完全可以對應成處理一套嵌套的玩具：

1. 目標：把一套 “二叉樹套娃” 的每一層左右反過來（比如大娃里的中娃左右互換，中娃里的小娃也左右互換）；
2. 處理方式：
   • 拿到一個娃（比如根節點4），先不管它本身，先把它左手里的小套娃（左子樹2）和右手里的小套娃（右子樹7）拆下來；
   • 分別把這兩個小套娃各自翻好（遞歸調用invertTree(2)和invertTree(7)，相當于把小套娃的內部全翻完）；
   • 再把翻好的兩個小套娃 “左右對調”，塞回大娃的手里；
3. 終止：拆到最后發現是個 “空殼”（root == null），沒有小套娃可拆，直接停下來。

二、用 “套娃” 看示例 1 的執行

原套娃結構（從外到內）：4（外層）→ 左手2、右手7?→?2的左手1、右手3；7的左手6、右手9。

1. 先拆4的右手7（先處理右子樹）：

   • 拆7的右手9：9沒有小套娃（左右都是null），翻完還是9，塞回7的左手；
   • 拆7的左手6：6沒有小套娃，翻完還是6，塞回7的右手；
   • 現在7的左右反過來了（左手9、右手6），整體塞回4的左手；

2. 再拆4原來的左手2：

   • 拆2的右手3：翻完還是3，塞回2的左手；
   • 拆2的左手1：翻完還是1，塞回2的右手；
   • 現在2的左右反過來了（左手3、右手1），整體塞回4的右手；

3. 最后4的左右（7和2）都翻好了，整個套娃就翻完了。

三、為什么 “套娃” 能 work？

因為翻轉二叉樹的每一層邏輯都完全相同—— 不管是外層的4，還是中間的2/7，甚至最內層的1/3，要做的事都是 “拆左右小套娃→翻小套娃→對調塞回去”。

遞歸之所以不用for/while，就是因為它把 “一層一層拆套娃” 的重復工作，交給了函數自己調用自己，而if (root == null)就是 “拆到最里面空殼” 的停止信號。

你能想到 “套娃” 這個比喻，其實已經抓住了遞歸的核心 ——重復處理相似的子問題，直到沒有子問題可處理，接下來只要多走幾遍簡單案例，就能從 “感覺像” 變成 “完全懂” 啦！

TreeNode left = invertTree(root.left);

TreeNode right = invertTree (root.right);

root.left = right; root.right = left;

//這一段代碼是按順序執行的話，那么后面的root.left經一次調用的時候，第二次是不是這個root已經變了？

這個問題問到了遞歸執行順序的關鍵 ——代碼會先完整執行完前兩行的遞歸調用，再執行后面的賦值操作，所以不存在 “后面調用時 root 已經變了” 的情況。咱們一步步拆解：

一、核心結論

這三行代碼的執行順序是 “先算完左右子樹的翻轉結果，再給當前 root 的左右賦值”，前兩行的遞歸調用不會受后兩行賦值的影響。

二、用 “執行步驟拆解” 看為什么

咱們把代碼拆成 “計算結果” 和 “修改當前節點” 兩個階段，對應到具體執行：

階段 1：計算 “翻轉后的左右子樹”（前兩行代碼）

java

運行

// 1. 先計算“翻轉后的左子樹”：調用invertTree處理root原本的left
TreeNode left = invertTree(root.left);  
// 2. 再計算“翻轉后的右子樹”：調用invertTree處理root原本的right
TreeNode right = invertTree(root.right);  

• 這兩步的核心是 “獲取結果”：不管遞歸調用多深，都會先把root原本的左子樹翻轉完，把結果存在left變量里；再把root原本的右子樹翻轉完，把結果存在right變量里。
• 此時，root本身的left和right還沒被修改（還是原來的樣子），因為第三、四行的賦值代碼還沒執行。

階段 2：修改當前 root 的左右子樹（后兩行代碼）

java

運行

// 3. 用之前算好的“翻轉后的右子樹”，覆蓋當前root的left
root.left = right;  
// 4. 用之前算好的“翻轉后的左子樹”，覆蓋當前root的right
root.right = left;  

• 這兩步才是 “修改當前節點”，而且用的是階段 1 已經算好的固定結果（left和right變量），和后續遞歸無關。

三、用 “套娃” 比喻再驗證

假設當前處理的是根節點4（原左 = 2，原右 = 7）：

1. 執行TreeNode left = invertTree(4.left)：其實就是去翻 “2這個套娃”，翻完后把結果（翻好的2，左 = 3、右 = 1）存在left里；
2. 執行TreeNode right = invertTree(4.right)：去翻 “7這個套娃”，翻完后把結果（翻好的7，左 = 9、右 = 6）存在right里；
3. 這時候才執行4.left = right（把翻好的7塞給4的左）、4.right = left（把翻好的2塞給4的右）。

整個過程中，翻2和翻7的時候，4的左右還是原來的2和7，完全沒被修改 —— 因為賦值操作是最后才做的。

四、關鍵誤區澄清

你擔心的 “第二次調用時 root 已經變了”，本質是誤以為 “執行第二行invertTree(root.right)時，第一行已經修改了 root”。但實際是：

• 前兩行都是 “讀取并處理 root 原本的左右子樹”，不修改 root；
• 只有等前兩行的遞歸全執行完，才會修改 root 的左右。

所以遞歸過程中，每個節點的 “原始左右子樹” 都是固定的，不會被提前修改，放心就好～

【我的意思是第一次交換過了左右節點，第二次回頭再來一遍這里的root就變了？】

你的疑問核心是 “會不會有第二次回頭處理同一個 root”—— 答案是不會！遞歸的邏輯是 “處理一個節點時，只處理一次，且處理完就不再回頭”，每個節點的 “左右交換” 只執行 1 次，不存在 “第二次再來一遍” 的情況。咱們從 “遞歸的調用鏈路” 和 “節點處理次數” 兩個角度說透：

一、遞歸是 “向下拆解，向上組裝”，每個節點只被 “處理一次”

遞歸處理二叉樹的過程，像 “從根節點往下拆套娃，拆到最內層后，再從內往外組裝”——每個節點只會在 “組裝到它” 的時候，執行一次交換邏輯，之后再也不會被這個遞歸流程重新處理。

用示例 1 的根節點4舉例，完整鏈路是：

1. 向下拆：處理4時，先去拆它的左子樹2?→ 拆2時，再去拆它的左子樹1?→?1沒有子節點（拆到最內層），直接返回1；
2. 向上裝：回到2，處理2的右子樹3（拆完返回3）→ 此時2的左右子樹都拆完，執行2的交換（左 = 3，右 = 1）→?2處理完，返回給4；
3. 再處理4的右子樹7（同樣 “拆→裝”，交換后返回7）；
4. 最后回到4，執行4的交換（左 = 7，右 = 2）→?4處理完，整個流程結束。

整個過程中，4、2、7、1、3、6、9每個節點都只被 “處理一次”（只執行一次自己的 “交換左右” 邏輯），處理完就作為結果返回給父節點，不會有 “第二次回頭處理同一個節點” 的情況。

二、為什么不會 “回頭”？因為遞歸的 “調用棧” 是 “先進后出”

遞歸的執行依賴 “調用棧”，每個函數調用會入棧，執行完會出棧，出棧后就不會再重新入棧（除非有新的調用，但這道題沒有）。

還是以4和2為例：

• 當調用invertTree(4)時，4的函數入棧；
• 然后調用invertTree(2)（處理4的左子樹），2的函數入棧；
• 再調用invertTree(1)（處理2的左子樹），1的函數入棧；
• 1處理完（無交換），出棧，回到2的函數；
• 2處理完（交換左右），出棧，回到4的函數；
• 4處理完（交換左右），出棧，整個流程結束。

每個節點的函數一旦出棧，就意味著它的 “處理已完成”，后續不會再重新入棧處理 —— 所以不存在 “第二次回頭，root 已經變了” 的場景。

三、一句話總結

遞歸處理二叉樹時，每個節點只被 “訪問并交換一次”，處理順序是 “先處理所有子節點，再處理當前節點”，子節點處理完不會回頭，當前節點處理完也不會再被重新處理，因此無需擔心 “root 被修改后再次調用” 的問題。

【有點像祖瑪游戲一個一個珠子過去，root只走一遍，但是每一次左右都換了】

這個比喻太形象了！完全命中了遞歸處理的核心 ——每個 “珠子”（節點）只走一遍，走的時候就把自己的 “左右裝飾”（左右子樹）換好，之后再也不回頭。咱們再順著這個比喻補一層細節，幫你徹底敲定邏輯：

一、“祖瑪珠子” 對應遞歸的 “節點處理順序”

把整棵二叉樹想象成一串 “祖瑪珠子”，珠子的順序是「從根到最左子樹→回退到父節點→再到右子樹」（也就是遞歸的 “深度優先” 順序），每個珠子只被 “捏過一次”：

1. 捏到一個珠子（比如節點2），先不換它的左右，而是先順著線捏它左邊的小珠子（1）；
2. 小珠子1沒有更小的珠子了（左右都是null），捏完直接放回去（無交換）；
3. 再捏2右邊的小珠子（3），同樣捏完放回去；
4. 現在回到2這個珠子，這時候才把它的 “左珠” 和 “右珠”（1和3）對調，換完后2就處理完了，再也不碰；
5. 接著回到上一顆大珠子（4），等它右邊的珠子（7）也按同樣邏輯捏完、換完，再把4的 “左珠”（換好的2）和 “右珠”（換好的7）對調。

二、“只走一遍” 對應 “節點不重復處理”

祖瑪游戲里珠子滾過就不會倒回來，遞歸里的節點也一樣：

• 每個節點的 “交換左右” 操作，只會在 “所有子節點都處理完” 后執行一次；
• 執行完交換，這個節點就作為 “處理好的成品”，傳遞給上一級節點（父節點），之后再也不會被這個遞歸流程重新訪問。
  比如節點2換完左右后，就變成了 “左3、右1” 的狀態，后續只有父節點4會把它當作 “成品珠子” 來用，不會再單獨拿出來重新換一次。

三、“每一次左右都換了” 對應 “遞歸的核心動作”

沒錯！每個珠子（非空節點）被 “捏到” 時，核心動作就是 “換左右”—— 但這個 “換” 是有前提的：

• 必須等它左右兩邊的 “子珠子串” 都先換好（遞歸處理完左右子樹），再換自己的左右；
• 換的時候用的是 “已經換好的子珠子串”（前兩行遞歸得到的left和right變量），不是沒處理過的原始子樹。

就像祖瑪里換珠子裝飾，得先把左右兩邊的小裝飾串做好，再往當前珠子上裝，裝完就固定了。

一句話收尾

你說的 “祖瑪珠子” 邏輯，完美對應了遞歸的「深度優先、節點唯一處理、先子后父交換”—— 每個節點只走一趟，走的時候就把左右換好，整個流程順下來，樹自然就翻過來了～

----------------------------------

最后手敲一遍吧！

/**
?* Definition for a binary tree node.
?* public class TreeNode {
?* ? ? int val;
?* ? ? TreeNode left;
?* ? ? TreeNode right;
?* ? ? TreeNode() {}
?* ? ? TreeNode(int val) { this.val = val; }
?* ? ? TreeNode(int val, TreeNode left, TreeNode right) {
?* ? ? ? ? this.val = val;
?* ? ? ? ? this.left = left;
?* ? ? ? ? this.right = right;
?* ? ? }
?* }
?*/
class Solution {
? ? public TreeNode invertTree(TreeNode root) {
? ? ? ? ? if (root == null){

? ? ? ? ? ? ? ? return null;

}

TreeNode left = invertTree(root.left);

TreeNode right?= invertTree(root.right);

root.left = right;

root.right = left;

return root;

? ? }
}

加油！(? ?_?)?